Grafi Pesati

Abbiamo il seguente problema:

Tre contenitori di capienza 4, 7 e 10 litri, inizialmente i contenitori da 4 e 7 sono pieni e quello da 10 vuoto. Possiamo soltanto versare acqua da un contenitori all’altro e fermarci solo quando il contenitore sorgente è vuoto o il destinazione è pieno.

Esiste una sequenza di operazioni che termina lasciando esattamente due litri d’acqua nel contenitore da 4 o da 7?

Possiamo modellare il problema con un grafo diretto dove i nodi sono i possibili stati di riempimento dei 3 contenitori, avremo quindi delle terne $(a,b,c)$ dove $a$ indica il contenitore da 4, $b$ quello da 7 e $c$ quello da 10.

Metteremo degli archi fra due nodi se è possibile passare fra lo stato di uno verso l’altro. Un frammento del grafo sarà quindi:

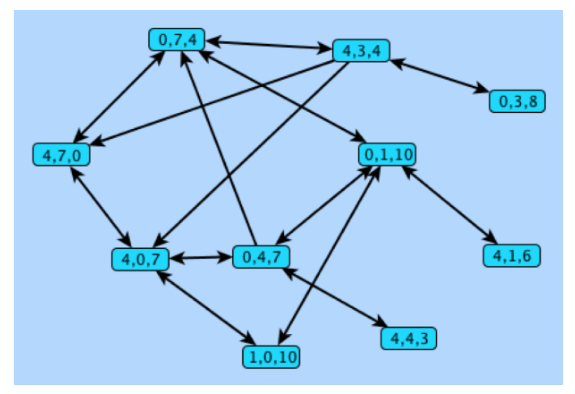
Per risolvere il problema dobbiamo capire se uno dei due nodi $(2,x,y),(x,2,y)$ è raggiungibile dal nodo $(4,7,0)$.

Abbiamo quindi modellato il problema per risolverlo con le visite, ad esempio possiamo usare una visita in ampiezza con costo $O(n+m)$ per la ricerca del cammino minimo.

Adesso però consideriamo una variante del problema, definiamo un’operazione “buona” se termina lasciando esattamente 2 litri in uno dei due contenitori; definiamo un’operazione “parsimoniosa” se il totale dei litri versati in tutti i versamenti è minimo rispetto a tutte le altre sequenza, ovvero che abbiamo spostato il minimo numero di litri.

Per modellare il problema in questo modo possiamo assegnare un costo ad ogni arco dove il costo sarà uguale ai litri spostati. Una porzione del grafo sarà quindi:

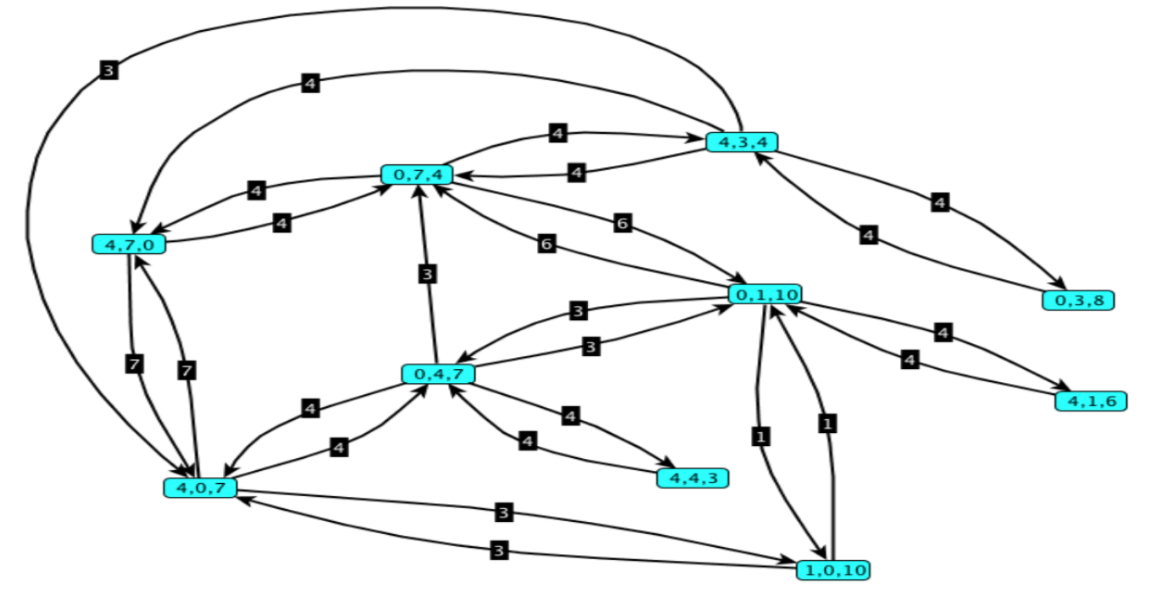
Adesso quindi non vogliamo più il cammino minimo a livello di archi percorsi ma il cammino minimo a livello di costo ovvero litri spostati.

---

Un’idea potrebbe essere quella di inserire dei nodi dummy ovvero fasulli negli archi, ad esempio se un arco pesa 3 inseriamo due nodi finti in modo che è come se attraversassimo 3 archi invece che 1:

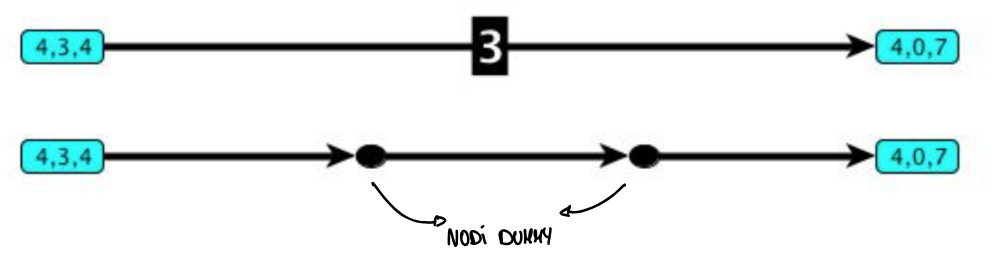
Questa soluzione è possibile però soltanto quando i costi degli archi sono interi e abbastanza piccoli altrimenti non è scalabile come soluzione.

---

Esiste un algoritmo che permette di trovare i cammini minimi quando si lavora su grafi pesati, questo funziona anche con pesi non interi ma non è detto che funzioni con pesi negativi.

Algoritmo di Dijkstra

L’algoritmo si basa sulla tecnica greedy, quindi fa di volta in volta la scelta migliore in quel momento e in futuro non cambia decisioni già prese.

L’algoritmo parte da un nodo sorgente e ad ogni passo aggiunge all’albero della ricerca l’arco che produce il nuovo cammino più economico per raggiungere un nuovo nodo, a questo nodo assegna il costo che abbiamo pagato per raggiungerlo.

Esempio

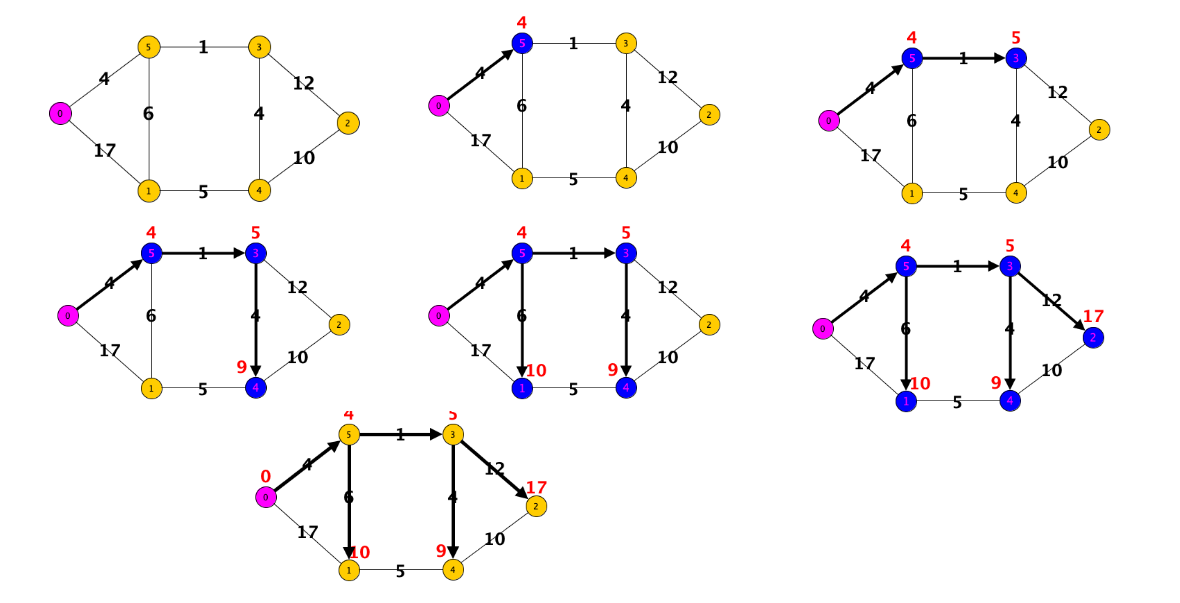
Come detto prima è importante notare che in caso di pesi negativi non è garantita la correttezza dell’algoritmo:

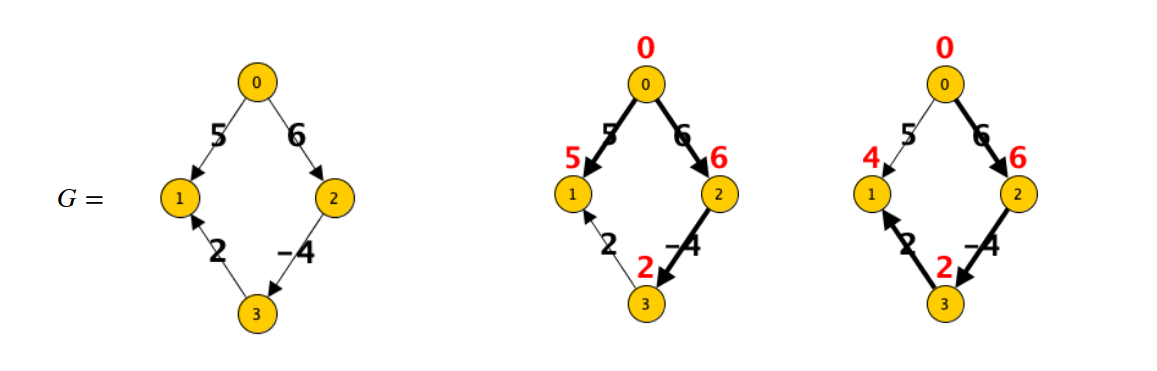
L’algoritmo percorrerebbe la soluzione centrale quando in realtà i percorsi minimi sono quelli sulla destra.

Dimostrazione

In pseudocodice possiamo vedere l’algoritmo in questo modo:

• $P[0\dots n-1]$ vettore dei padri inizializzato a -1
• $D[0\dots n-1]$ vettore delle distanze inizializzato a infinito
• Nodo $s$ come sorgente quindi $D[s]=0$
• while esistono archi {x,y} con P[x] != -1 e P[y] == -1:
  • Sia {x,y} quello per cui è minimo D[x] + peso(x,y) allora D[y], P[y] = D[x] + peso(x,y), x
• return P,D

Dato che ad ogni iterazione del while viene assegnata una nuova distanza ad uno dei nodi del grafo, dimostriamo per induzione sul numero di iterazioni che la distanza assegnata è quella minima.

• Caso Base: La sorgente ha come distanza 0 dato che banalmente non possono esserci percorsi inferiori. (Sempre considerando grafi senza pesi negativi)

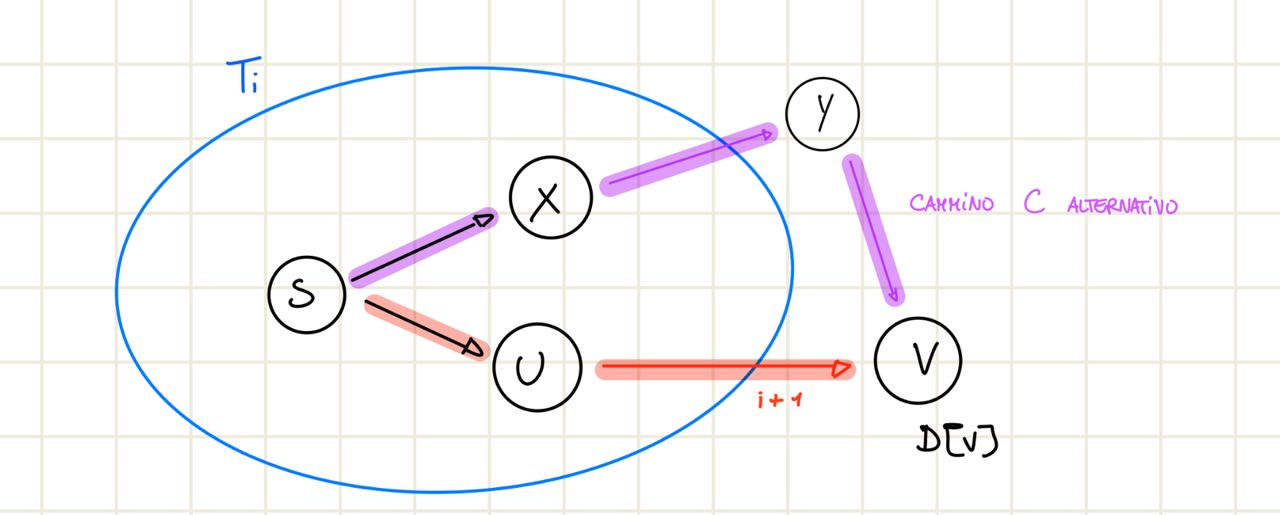
Abbiamo $T_i$ l’albero costruito dalla ricerca al passo $i$.

• Al passo $i+1$ l’algoritmo aggiunge l’arco $(u,v)$, mostriamo che $D[v]$ appena ottenuta è quella minore considerando un possibile percorso alternativo $C$.
• Sia $C$ un qualsiasi cammino da $s$ a $v$ alternativo a quello presente nell’albero e $(x,y)$ il primo arco che incontriamo percorrendo $C$ tale che $x$ è nell’albero $T_i$ e $y$ no.

Questo arco deve esistere perché l’algoritmo percorre in ordine: $(s,u),(s,x)$ e secondo l’ipotesi $(u,v)$ quindi se esiste un percorso alternativo sicuramente non è $(x,v)$ altrimenti sarebbe stato scelto, deve esistere quindi un arco che ci porta fuori $T_i$ ovvero $(x,y)$ e che poi ci porta a $u$ ovvero $(y,v)$.

• Adesso per ipotesi induttiva sappiamo che $\text{costo(C)}\ge D[x]+\text{peso(x,y)}$ dato che $C$ è composto anche da un altro arco.
• Ma se l’algoritmo ha preferito percorrere $(u,v)$ significa che $D[x]+p(x,y)\ge D[u]+p(u,v)$
• Da cui segue che $\text{costo(C)}\ge D[x]+p(x,y)\ge D[u]+p(u,v)=D[v]$
• Quindi abbiamo appena mostrato che il cammino alternativo ha costo maggiore al percorso trovato dall’algoritmo.

---

Implementazione

Per rappresentare un grafo pesato avremo che se un arco $(x,y)$ costa $c$ nella lista di adiacenza di $x$ avremo, associato insieme ad $y$, il costo $c$. Quindi avremo le liste di adiacenza composte da delle coppie.

Inoltre, utilizziamo un vettore lista, dove per ogni nodo $x$ memorizziamo una terna formata da (definitivo, costo, origine) dove:

• Definitivo: Un flag che assume 1 se il costo per raggiungere $x$ è stato definitivamente stabilito. Se 0 allora il costo per $x$ è ancora in aggiornamento
• Costo: Rappresenta il costo minimo in quel momento per raggiungere $x$ dalla sorgente. Inizialmente vale infinito per tutti i nodi tranne che per la sorgente dove vale 0.
• Origine: Indica il nodo padre lungo il cammino dalla sorgente ad $x$, se non è ancora stato trovato un percorso e quindi un padre per $x$ allora vale -1.

Questa lista inizialmente sarà quindi in questo stato:

$$lista[x]=\{\begin{array}{l}(1,0,s)\text{se }x=s\\ (0,costo,s)\text{ se }(costo,x)\in G[s]\\ (0,+\infty ,-1)\text{altrimenti}\end{array}$$

Si avranno poi delle iterazioni dove:

1. Si scorre l’intera Lista per individuare il nodo $x$ con il flag a 0 ovvero con il percorso non ancora stabilito e che ha il costo minimo, questo sarà il candidato per il quale il cammino minimo dalla sorgente è noto.
2. Se il costo minimo che troviamo è infinito significa che non ci sono altri nodi raggiungibili, il ciclo si interrompe
3. Il nodo $x$ trovato viene aggiornato impostando il flag 1 e impostando quindi il suo costo come definitivo, questo non verrà più modificato.
4. Aggiorniamo tutti i vicini di $x$, per ogni nodo $y$ vicino ad $x$ se $y$ non è ancora definitivo e il nuovo costo ottenuto passando per $x$ è inferiore al costo attuale memorizzato per $y$ allora si aggiorna il costo di $y$.

def dijkstra(s, G):
	n = len(G)
	Lista = [(0, float('inf'), -1)] * n
	Lista[s] = (1, 0, s)
	for y, costo in G[s]:
		Lista[y] = (0, costo, s)
	while True:
		minimo, x = float('inf'), -1
		for i in range(n):
			if Lista[i][0] == 0 and Lista[i][1] < minimo:
				minimo, x = Lista[i][1], i
		if minimo == float('inf'):
			break
		definitivo, costo_x, origine = Lista[x]
		Lista[x] = (1, costo_x, origine)
		for y, costo_arco in G[x]:
			if Lista[y][0] == 0 and minimo + costo_arco < Lista[y][1]:
				Lista[y] = (0, minimo + costo_arco, x)
 
 
	D,P = [costo for _, costo, _ in lista], [origine for _, _, origine in Lista]
	return D,P

• Le operazioni fuori dal while costano $\Theta (n)$
• Il while lo eseguiamo al più $O(n-1)$ volte e all’interno abbiamo:
  • Il primo for che viene iterato $n$ volte
  • Il secondo for che viene eseguito al più $n$ volte
• Il while costa quindi $\Theta (n^2)$ che è anche la complessità dell’implementazione

Questa è quindi ottima nel caso di grafi densi dove si ha che $m=\Theta (n^2)$.

Infatti notiamo che se si potesse evitare di scorrere ogni volta il vettore Lista alla ricerca del minimo, eviteremmo di pagare $\Theta (n)$ ad ogni iterazione del while, possiamo farlo sostituendo Lista con un heap minimo che ci fornisce il minimo in tempo logaritmico

def dijkstra1(s, G):
 
    n = len(G)
    D = [float('inf')] * n  # Distanze inizialmente infinite
    P = [-1] * n  # Predecessori inizializzati a -1
    # la sorgente dista 0 da se stessa
    D[s] = 0
    # La sorgente è la radice dell'albero delle distanze
    P[s] = s
    H = []  # Min-heap
    # Inizializziamo l'heap con i vicini della sorgente
    for y, costo in G[s]:
        heappush(H, (costo, s, y))  # (costo, x=s, y)
    
    while H:
        # Estrai il nodo con distanza minore
        costo, x, y = heappop(H)
        if P[y] == -1:
            # inserisci y nel vettore dei padri come figlio di x
            P[y] = x
            # setta la distanza minima di y
            D[y] = costo
            for v, peso in G[y]:
                # Esplora i vicini di y
                if P[v] == -1:
                    # Se v non è ancora stato aggiunto all'albero
                    heappush(H, (D[y] + peso, y, v))
    
    # Restituisce le distanze e i predecessori
    return D, P
 

Con questa implementazione otteniamo un costo di $O(n\log n)+O(m\log n)+O(m\log n)=O((n+m)\log n)$

Quindi possiamo dire che:

• L’implementazione $O(n^2)$ è ottimale in grafi densi
• La seconda è ottimale in grafi sparsi ma andrebbe evitata in grafi densi dato che otteniamo $O(n^2\log n)$

Da notare che esistono altre implementazioni più efficienti che utilizzano altre strutture come l’heap di Fibonacci e dove il tempo d’esecuzione scende a $O(m+n\log n)$

Minimo Albero di Copertura

Dato un grafo G andiamo a cercare al suo interno un albero (grafo connesso aciclico) che “copre” l’intero grafo e la somma dei costi dei suoi archi sia minima.

Un algoritmo importante per risolvere questo problema è l’algoritmo di Kruskal:

• Parti con il grafo T che contiene tutti i nodi di G e nessun arco
• Considera uno dopo l’altro gli archi di G in ordine di costo crescente
• Se l’arco forma ciclo in T con archi già presi allora non lo prendiamo
• Restituire T

Anche questo algoritmo rientra nel paradigma della tecnica greedy ovvero prendere le giuste decisioni in quel momento e non cambiarle mai più.

Esempio

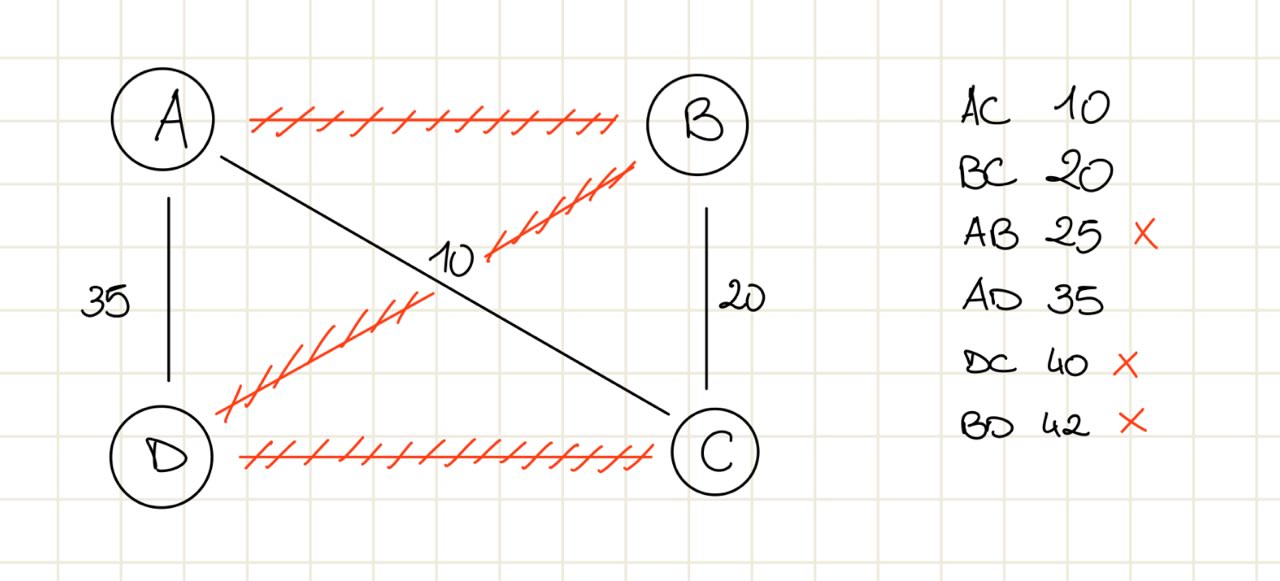
Prova di correttezza

Dobbiamo mostrare che se al termine otteniamo T come albero di copertura allora non esiste albero che costa meno.

Dimostrazione che otteniamo un albero un po’ meh :(

Mostriamo per assurdo che è l’albero di copertura con costo minore:

Tra tutti gli archi di copertura di costo minimo per G prendiamo quello che differisce meno da T (quello ottenuto dall’algoritmo) e lo chiamiamo $T^{\ast }$.

Supponiamo quindi per assurdo che $T$ differisca da $T^{\ast }$.

Prendiamo gli archi $e_1,e_2,\dots$ nello stesso ordine in cui sono stati presi nel corso dell’algoritmo e sia $e$ il primo arco preso che non compare in $T^{\ast }$, questo significa che se lo inseriamo in $T^{\ast }$ otteniamo un ciclo $C$.

Allora il ciclo $C$ contiene almeno un arco $e^{\prime }$ che non appartiene a $T$ infatti non tutti gli archi di $C$ sono in $T$ altrimenti $e$ non sarebbe stato preso dall’algoritmo. Appunto perché in $T$ abbiamo $e$ (dato che non è in $T^{\ast }$) quindi deve essercene un altro che non è presente in $T$ (da quanto ho capito io).

Consideriamo adesso l’albero $T^{\prime }$ che si ottiene da $T^{\ast }$ inserendo l’arco $e$ ed eliminando $e^{\prime }$ e notiamo che il costo di $T^{\prime }$ è uguale a $\text{costo}(T^{\ast })-\text{costo}(e^{\prime })+\text{costo}(e)$ e che non può aumentare rispetto a quello di $T^{\ast }$ perché $\text{costo(e)}\le \text{costo}(e^{\prime })$ infatti fra i due Kruskal ha scelto prima $e$ (credo nella costruzione di $T^{\prime }$) ma allora $T^{\prime }$ è un altro albero di copertura ottimo che differisce da $T$ in meno archi di quanto faccia $T^{\ast }$ e contraddice l’ipotesi iniziale dove $T^{\ast }$ differisce da $T$ nel minor numero di archi.

Implementazione

def kruskal(G):
	E = [(c, u, v) for u in range(len(G)) for v,c in G[u] if u<v]
	E.sort()
	T = [[] for _ in G]
	for c, u, v in E:
		if not connessi(u, v, T):
			T[u].append(v)
			T[v].append(u)
	return T
 
 
def connessi(u, v, T):
	def DFSr(a, b, T, visitati):
		visitati[a] = 1
		for z in T[a]:
			if z == b:
				return True
			if not visitati[z]:
				if DFSr(z, b, T, visitati):
					return True
		return False
 
	visitati = [0] * len(T)
	return DFSr(u, v, T, visitati)

• L’ordinamento esterno al for costa $O(m\log m)=O(m\log n^2)=O(m\log n)$
• Il for viene iterato $m$ volte e la procedura connessi richiede $O(n)$ quindi in totale il for $O(m\cdot n)$

La complessità totale dell’operazione risulta quindi $O(m\cdot n)$

---

Tramite delle strutture in C chiamate UNION e FIND possiamo ridurre la complessità a $O(m\log n)$

La Union Find è una struttura dati che permette le seguente operazioni:

• UNION(a, b, C) fonde due componenti connesse a e b in C in tempo O(1)
• FIND(x, C) trova in C la componente connessa in cui si trova il nodo x in tempo $O(\log n)$

def kruskal1(G):
	E = [(c,u,v) for u in range(len(G)) for v,c in G[u] if u<v]
	E.sort()
	T = [[] for _ in G]
	C = Crea(T)
	for c, u, v in E:
		cu = FIND(u, C)
		cv = FIND(v, C)
		if cu != cv:
			T[u].append(v)
			T[v].append(u)
			Union(cu, cv, C)
	return T

Dove abbiamo:

def Crea(G):
	C = [(i, 1) for i in range(len(G))]
	return C
 
 
def Find(u, C):
	while u != C[u]:
		u = C[u]
	return u
 
 
def Union(a, b, C):
	tota, totb = C[a][1], C[b][1]
	if tota >= totb:
		C[a] = (a, tota + totb)
		C[b] = (a, totb)
	else:
		C[b] = (b, tota + totb)
		C[b] = (a, totb)

• L’ordinamento costa sempre $O(m\log n)$

• Il for lo iteriamo $m$ volte e al suo interno:

  • L’estrazione dell’arco minimo richiede $\Theta (1)$
  • Il FIND costa $O(\log n)$
  • L’Union costa $\Theta (1)$

• Quindi in totale il for costa $O(m\log n)$ che sarà anche il costo totale dell’algoritmo

• Struttura Dati per Insiemi Disgiunti

• Cammini con Pesi Negativi