La Union - Find nota anche come Disjoint Set Union (DSU) è una struttura dati usata per gestire insiemi disgiunti, permette di effettuare operazioni di unione e ricerca efficienti su insiemi disgiunti.

Ci sono 3 operazioni fondamentali:

Crea(S): Restituisce una struttura dati Union-Find sull’insieme S di elementi dove ciascun elemento è in un insieme separato
Find(x, C): Restituisce il nome dell’insieme della struttura dati C a cui appartiene l’elemento x
Union(A, B, C): Modifica la struttura C fondendo la componente A con la componente B e restituisce il nome della nuova componente

Questo tipo di struttura è utile ad esempio per gestire l’evoluzione di un grafo quando aggiungiamo archi, in questo caso le componenti connessi sono gli insiemi disgiunti. Quindi tramite l’operazione find riusciamo a determinare a quale componente appartiene un nodo e quindi capire anche se due nodi appartengono alla stessa componente, banalmente se find(a) == find(b).

Se ad esempio si aggiunge l’arco (u,v) al grafo, si controlla se i due nodi sono nella stessa componente e se non lo sono allora abbiamo:

A = find(u)
B = find(v)
Possiamo ottenere il nuovo grafo con Union(A, B)

Ma cosa indichiamo con nome dell’insieme?

Dipende da caso a caso, nelle successive implementazioni sceglieremo come nome dell’insieme quello di un particolare elemento di tale insieme, come ad esempio l’elemento massimo presente in esso.

Implementazione

Il modo più semplice per implementarla su n elementi è quella di mantenere il vettore C delle n componenti. All’inizio ogni elemento è separato dagli altri e quindi abbiamo n componenti diversi, quindi per ogni i si ha C[i] = i.

Quando la componente i viene fusa con j:

Se $i > j$ allora tutte le occorrenze di $j$ in $C$ vengono sostituite da $i$
Se $j > i$ allora tutte le occorrenze di $i$ vengono sostituite da $j$

def Crea(G):
	C = [i for i in range(len(G))]
	return C
 
def Find(u, C):
	return C[u]
 
def Union(a, b, C):
	if a > b:
		for i in range(len(C)):
			if C[i] == b:
				C[i] = a
	else:
		for i in range(len(C)):
			if C[i] == a:
				C[i] = b

Dove:

Crea ha costo $Θ (n)$
Find ha costo $Θ (1)$
Union ha costo $Θ (n)$

Proviamo a bilanciare i costi ovvero pagare qualcosa in più per la FIND e qualcosa in meno per la UNION, usiamo il vettore dei padri.

FIND: Quando voglio sapere in che componente si trova un nodo devo risalire la radice, $O (n)$ .
UNION: Quando fondo due componenti una diventa figlia dell’altra, $O (1)$

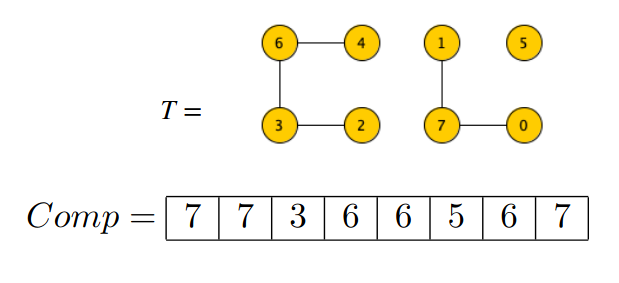
Se fondiamo le componenti otteniamo:

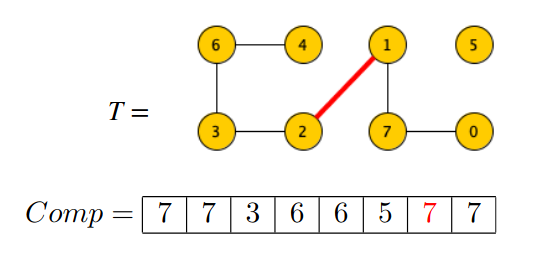
Dobbiamo vedere il nodo maggiore come radice dell’albero della componente, ovvero:

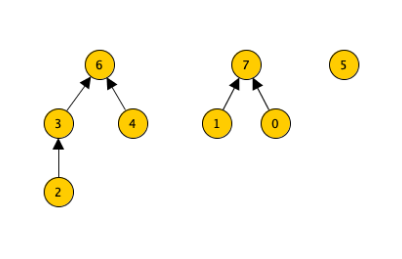
Dal quale poi otteniamo:

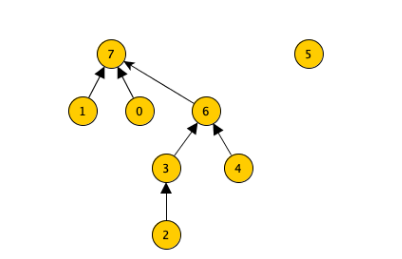
Unendo le componenti.

Per implementare questa idea:

def Crea(G):
	C = [i for i in range(len(G))]
	return C
 
def Find(u, C):
	while u != C[u]:
		u = C[u]
	return u
 
def Union(a, b, C):
	if a > b:
		C[b] = a
	else:
		C[a] = b

Dove abbiamo:

Crea $Θ (n)$
Find $O (n)$
Union $Θ (1)$

Non vogliamo che l’operazione FIND abbiamo un costo elevato ovvero che i cammini per raggiungere le radici siano troppo lunghi, per evitare questo dobbiamo mantenere gli alberi bilanciati

Per fare questo, quando facciamo una UNION fra due componenti scegliamo sempre come nuova radice quella che ha il maggior numero di elementi, in questo modo per almeno la metà dei nodi presenti nelle due componenti la lunghezza fino alla radice non cambia.

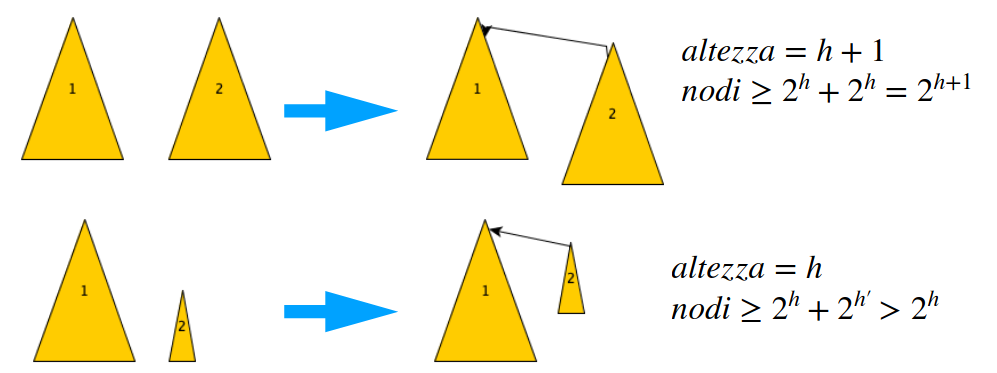
Fondendo due componenti e rispettando l’idea di prima garantiamo la seguente proprietà:

Se un insieme ha altezza $h$ allora l’insieme contiene almeno $2^{h}$ elementi

E da questo possiamo dire che l’altezza non potrà mai superare $lo g_{2} n$ altrimenti avremmo più di $n$ nodi che è un assurdo.

In questo modo otteniamo una FIND da $O (lo g n)$

Facciamo in modo quindi che ai nodi radice sia associato anche il numero di elementi che la loro componente contiene. Ogni elemento è caratterizzato da una coppia (x, numero) dove x è il nome dell’elemento e numero è il numero di nodi nell’albero radicato in x

def Crea(G):
	C = [(i, 1) for i in range(len(G))]
	return C
 
def Find(u, C):
	while u != C[u]:
		u = C[u]
	return u
 
def Union(a, b, C):
	tota, totb = C[a][1], C[b][1]
	if tota >= totb:
		C[a] = (a, tota + totb)
		C[b] = (a, totb)
	else:
		C[a] = (b, tota)
		C[b] = (b, tota + totb)

Dove abbiamo:

Crea $Θ (n)$
Find $O (lo g n)$
Union $O (1)$

Dimostriamo la correttezza della proprietà secondo la quale se un insieme ha altezza $h$ allora l’insieme contiene almeno $2^{h}$ elementi

Assumiamo per assurdo che durante un’unione si sia formata una nuova componente di altezza $h$ che non rispetta la proprietà. Consideriamo che questa sia la prima volta che succede e chiamiamo le due componenti ca e cb, allora possono essersi verificati due casi:

ca cb avevano la stessa altezza, allora avevano altezza $h - 1$ ed ognuna aveva almeno $2^{h - 1}$ elementi, quindi la nuova componente avrà $2^{h - 1} + 2^{h - 1} = 2^{h}$ e quindi la proprietà è verificata
ca cb avevano altezze diverse ma allora l’altezza dopo la fusione è quella della componente di altezza maggiore che doveva essere $h$ e quindi conteneva già da sola $2^{h}$ elementi

👨🏻‍💻 Alem's Notes

Struttura Dati per Insiemi Disgiunti

Implementazione

Backlinks