Cammini con Pesi Negativi

Dato un grafo G e un nodo s vogliamo determinare le distanze minime da questo nodo anche se sono presenti archi con presi negativi.

Per fare questo è importante definire prima il concetto di ciclo negativo ovvero un ciclo dove la somma dei pesi degli archi è negativa;.

Esempio

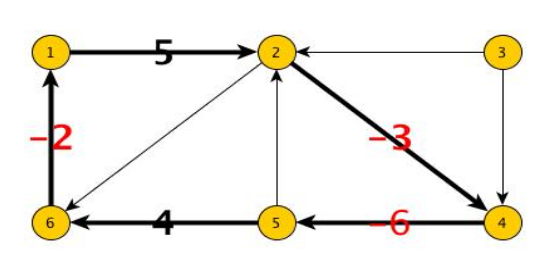
Infatti: 5-3-6+3-2=-2

Ci serve questa definizione perché se tra due nodi è presente un ciclo negativo allora non esiste un cammino di costo minimo fra questi due, infatti potremmo percorrere il ciclo quante volte vogliamo per abbassare il costo.

Quindi per risolvere il problema di prima non possiamo prendere un grafo qualsiasi G ma un grafo senza cicli negativi.

Algoritmo di Bellman - Ford

Se il grafo G non contiene cicli negativi, allora per ogni nodo t raggiungibile dalla sorgente s esiste un cammino di costo minimo che attraversa al più n - 1 archi.

Infatti se avessimo più di n-1 archi attraversati significherebbe che almeno un nodo è ripetuto e quindi formerebbe un ciclo. Infatti non avendo cicli negativi, la presenza di altri cicli non influenza il costo, questi infatti verranno ignorati e raggiungeremo i nodi in al più n-1 archi.

Per l’algoritmo definiamo quindi la seguente tabella T di dimensione n x n dove:

• T[i][j] = costo di un cammino minimo da s al nodo j di lunghezza al più i

La soluzione al nostro problema sarà data dall’ultima riga. Inoltre possiamo già individuare alcuni valori:

• La prima riga avrà tutti $-\infty$ ad eccezione della sorgente che avrà $0$
• La sorgente inoltre avrà sempre costo 0

Come calcoliamo i restanti valori?

Dobbiamo distinguere i due casi:

• Se il costo per raggiungere j ha lunghezza inferiore o uguale al valore i allora prendiamo il valore precedente della tabella, quindi T[i][j] = T[i][j - 1]

• Se non è così allora deve esistere un cammino minimo di lunghezza più i - 1 ad un nodo x il quale poi tramite un arco ci porterà a j. Dobbiamo quindi prendere il cammino minimo fra tutti questi cammini che ci portano dalla sorgente ad un x e da x a j tramite un solo arco, ovvero:

  $T[i][j]=mi{n}_{(x-1)\in E}(T[i-1][x]+costo(x,j))$

E è l’insieme degli archi

Ovviamente non sappiamo in quale dei due casi ci troviamo e quindi prendiamo il minore fra questi due casi:

$$T[i][j]=min(T[i][j]=T[i][j-1],mi{n}_{(x-1)\in E}(T[i-1][x]+costo(x,j)))$$

---

Per aumentare l’efficienza dell’algoritmo dato che è necessario conoscere gli archi entranti al nodo j, conviene calcolare il grafo trasposto GT di G, in questo modo in GT[j] avremo tutti i nodi x tali che in G esiste l’arco x -> j

Implementazione

def CostoCammini(G, s):
	n = len(G)
	inf = float('inf')
	T = [[inf] * n for _ in range(n)]
	T[0][s] = 0
	GT = Trasposto(G)
	for i in range(1, n):
		for j in range(n):
			T[i][j] = T[i - 1][j]
			if j != s:
				for x, costo in GT[j]:
					T[i][j]=min(T[i][j], T[i-1][x] + costo)
	return T[n-1]
 
def Trasposto(G):
	n = len(G)
	GT = [[] for _ in G]
	for i in range(n):
		for j, costo in G[i]:
			GT[j].append((i, costo))
	return GT

• La tabella costa $\Theta (n^2)$
• Calcolare il trasposto $O(n+m)$
• I due for più interni in realtà scorrono le liste di adiacenza dei nodi quindi hanno un costo totale di $\Theta (m)$ mentre quello esterno $\Theta (n)$. In totale i 3 for costano $\Theta (nm)$

Costo totale: $O(n^2+nm)$

Implementazione per trovare i cammini

Oltre al costo per raggiungere i nodi ci interessa trovare anche i nodi da percorrere, dobbiamo modificare l’algoritmo in modo che ci restituisca il vettore dei padri.

Possiamo farlo mantenendo per ogni nodo j il suo predecessore e aggiornare il valore P[j] ogni volta che il valore T[k][j] cambia ovvero troviamo un percorso minore

def CostoCammini(G, s):
	n = len(G)
	inf = float('inf')
	T = [[inf] * n for _ in range(n)]
	P = [-1] * n
	T[0][s] = 0
	P[s] = s
	GT = Trasposto(G)
	for k in range(1, n):
		for j in range(n):
			if j == s:
				T[k][j] = 0
			else:
				for x, costo in GT[j]:
					if T[k-1][x] + costo < T[k][j]:
						T[k][j]=T[j-1][x] + costo
						P[i] = x
	return T[n-1], P

---

Ottimizzazioni:

• Se notiamo che una riga è uguale alla precedente allora anche le righe successive non cambieranno, possiamo quindi terminare l’algoritmo.
• Non serve avere sempre in memoria l’intera tabella, ci basta l’ultima riga e la precedente. In questo modo riduciamo la complessità di spazio da $O(n^2)$ a $O(n)$

Inoltre questo algoritmo non si accorge se ci sono o no cicli negativi, se vogliamo però effettuare un test, ci basta calcolare i percorsi fino a distanza $n$, aggiungendo quindi una riga.

Le ultime due righe $n-1$ e $n$ saranno uguali se e solo se nel grafo non ci sono cicli negativi raggiungibili da $s$. Implementare il test non cambia l’asintotica dell’algoritmo.