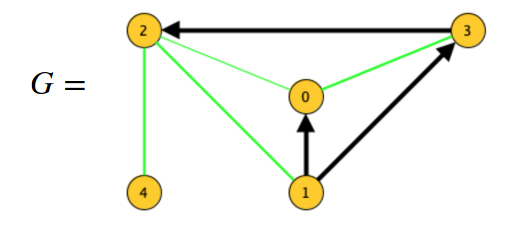
Il grafo è una struttura dati che indichiamo con $G (V, E)$ dove $V$ è un insieme di nodi e $E$ è un insieme di archi che collegano i nodi.

Indichiamo con:

$∣ V ∣ = n$
$∣ E ∣ = m$

Possiamo fare due distinzioni:

Grafo Diretto - $0 \leq m \leq n (n - 1) = O (n^{2})$
Grafo non Diretto - $0 \leq m \leq \frac{n ( n - 1 )}{2} = O (n^{2})$

Un grafo è diretto quando gli archi hanno una direzione mentre non diretto quando non la hanno e quindi possiamo “percorrere” l’arco in entrambe le direzioni.

Altre distinzioni che possiamo fare sono:

Grafo Sparso - Si dice sparso se $m = O (n)$ quindi il numero di archi è al massimo uguale al numero di nodi.
Grafo Denso - Si dice denso se $m = Ω (n^{2})$ quindi il numero di archi è almeno uguale al quadrato del numero di nodi. In questo tipo di grafi possiamo fare ulteriori distinzioni in:
- Grafo Completo - Se ha tutti gli archi e quindi $m = Θ (n^{2})$
- Torneo - Se il grafo è diretto e se tra ogni coppia di nodi c’è esattamente un arco e quindi $m = Θ (n^{2})$

Nota

Si usa $Ω (n^{2})$ per i grafi densi perché siccome il numero massimo di archi è dato da $\frac{n ( n - 1 )}{2}$ in asintotica otteniamo comunque $n^{2}$ , questo anche per i grafi non orientati con $2$ al denominatore.

Inoltre da notare che un grafo non sparso non è necessariamente denso dato che potrebbe avere ad esempio $Θ (n lo g n)$ archi.

Esempio 1 - Un esempio di grafo sparso è l’albero, questo è un grafo sparso e senza cicli, inoltre ha sempre $m = n - 1$ archi e si può provare per induzione

Esempio 2 - Altri grafi non sparsi sono i grafi planari, sono dei grafi che possono essere disegnati sul piano senza che gli archi si intersechino, ovviamente se disegnato nel modo corretto, infatti:

Nota

Da notare che gli alberi sono un sottoinsieme dei grafi planari, inoltre se un grafo è un albero allora è sicuramente planare ma non è vero il contrario.

Teorema Eulero

Un grafo planare di $n > 2$ nodi ha al più $3 n - 6$ archi

Osservando la tabella deduciamo quindi che da $n = 5$ in poi esistono di certo grafi non planari, essenzialmente la tabella mi dice che se ad esempio ho 5 nodi e disegno 10 archi è impossibile avere un grafo planare ma se ne disegno 9 ho la possibilità di fare un grafo planare.

Altre definizioni sui grafi:

Grafo Connesso

Presa una qualsiasi coppia di nodi questi sono connessi fra loro tramite un qualsiasi percorso, possiamo trovare anche un sottografo di un grafo con questa proprietà, questo prende il nome di componente connessa.

Un concetto legato alla connessione è la raggiungibilità ovvero un’operazione tra due nodi che ci dice se da uno possiamo raggiungere l’altro.

Da notare che in futuro introdurremmo la connessione forte per i grafi diretti dato che questa semplice non ha molto senso per quest’ultimi infatti se abbiamo un nodo A che porta ad un nodo B non è detto che il nodo B ci porti al nodo A.

Grafi tramite Matrici Binarie

Presi due nodi $i, j$ usati come coordinate per accedere alla matrice, il valore $M [i] [j] = 1$ se e solo se c’è un arco diretto da $i$ a $j$ altrimenti $0$ .

Questa prende il nome di matrice di adiacenza.

Esempio:

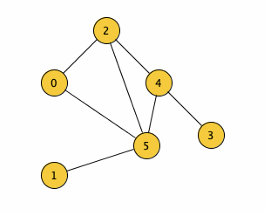
Otteniamo la matrice:

001001000001100011000010001101111010

Infatti ogni riga ci indica un nodo quindi la prima sarà il nodo 0, la seconda il nodo 1 ecc…

All’intersezione fra riga e colonna troviamo il valore 1 se il nodo $i$ della riga punta al nodo $j$ della colonna.

In questo caso il grafo non è diretto quindi troviamo se c’è un arco in generale non interessandoci della direzione, nel caso avessimo avuto un grafo diretto ci saremmo preoccupati del senso dell’arco.

Nota

Da notare che nella diagonale sono presenti soltanto $0$ dato che non ci sono archi che nascono e muoiono su se stessi.

Trovare un Pozzo

In un grafo un pozzo è un nodo senza archi uscenti, inoltre si dice pozzo universale se un nodo è un pozzo e inoltre tutti gli altri nodi hanno un arco che punta verso di lui.

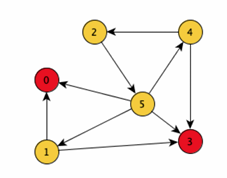
In questo caso 0 e 3 sono dei pozzi.

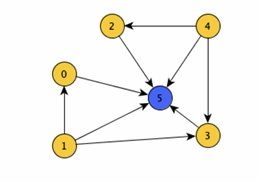
Qui invece 5 è un pozzo universale.

Come possiamo trovare un pozzo facilmente? - Ci basta controllare la matrice di adiacenza e trovare un nodo la cui lista non contiene valori 1 ovvero non ha archi uscenti.
Se vogliamo trovare il (pozzo universale unico) pozzo universale? Oltre a controllare che il nodo sia un pozzo come visto sopra dobbiamo controllare se la colonna di quel nodo abbia invece tutti valori 1 (tranne su se stesso) ovvero che tutti gli altri nodi puntino verso di lui.

Quindi cerchiamo questo:

Possiamo usare un algoritmo che ha costo $Θ (n)$ per verificare se un grafo ha un pozzo universale, questo algoritmo prende due nodi del grafo e controlla il valore della loro intersezione, quindi ad esempio:

Prendiamo i nodi $i, j$ e controlliamo:

M [i] [j] = {1 i non \overset{e}{ˊ} pozzo 0 j non \overset{e}{ˊ} pozzo universale

Questo perché se la cella vale 1 allora $i$ ha un nodo verso $j$ ma allora non può essere pozzo dato che ha un arco uscente, inoltre se troviamo uno 0 allora $j$ non è pozzo universale dato che non tutti i nodi (in questo caso $i$ ) hanno un arco verso di lui, potrebbe ancora essere pozzo.

Con ogni test eliminiamo un nodo dai possibili pozzi universali, dopo $n - 1$ test ci rimane un solo nodo da controllare.

def pozzoU2(M):
    '''restituisce True se il grafo M ha pozzo universale, False Altrimenti'''
    L=[x for x in range(len(M))]
    while len(L)>1:
        a=L.pop()
        b=L.pop()
        if M[a][b]:
            L.append(b)
        else:
            L.append(a)
    x=L.pop()
    for j in range(len(M)):
        if M[x][j]: return False
    for i in range(len(M)):
        if i!=x and M[i][x]==0: return False
    return True

Il primo while lascia nella lista L soltanto un candidato a pozzo universale facendo i test visti prima. Una volta trovato si controlla che lui non abbia archi uscenti verso altri nodi e che tutti gli archi escluso se stesso abbiano un arco entrante verso di lui.

Grafi tramite Liste di Adiacenza

Un altro modo per rappresentare i grafi è quello delle liste di adiacenza, utilizziamo un dizionario che ha come chiavi i nodi e come valore una lista contenente tutti i nodi collegati a quel nodo valore.

Questa a differenza della matrice ci permette di inserire i nodi anche in modo non consecutivo e presenta alcuni vantaggi e svantaggi a seconda del grafo:

Per quanto riguarda lo spazio questa occupa $O (n + m)$ che per grafi sparsi ci fa risparmiare spazio rispetto alla matrice mentre se abbiamo un grafo denso abbiamo lo stesso costo dato che otteniamo $O (n + n^{2}) = O (n^{2})$ uguale alla matrice.

In grafi sparsi non ci costa molto scorrere la lista alla ricerca di un arco ma nel caso peggiore ovvero in grafi densi può costarci anche $O (n)$ mentre per la matrice abbiamo sempre tempo costante anche in grafi densi.

Un esempio di rappresentazione (senza uso di dizionario, non possiamo quindi inserire in modo sparso i nodi) è quindi:

G = [
	[2,5],
	[5],
	[0,4,5],
	[4],
	[2,3,5],
	[0,1,2,4]
]

In generale chi e quando scegliere?

Matrice

Se abbiamo un numero di archi vicino a $n^{2}$ ovvero un grafo denso e se dobbiamo controllare frequentemente l’esistenza di archi o in generale vogliamo accessi costanti.

Lista di adiacenza

Se abbiamo un grafo sparso, vogliamo risparmiare memoria e dobbiamo iterare sui nodi adiacenti di un nodo.

Visite nei Grafi

Dato un grafo $G$ ed un suo nodo $u$ vogliamo sapere quali nodi del grafo sono raggiungibili da $u$ .

Esempio

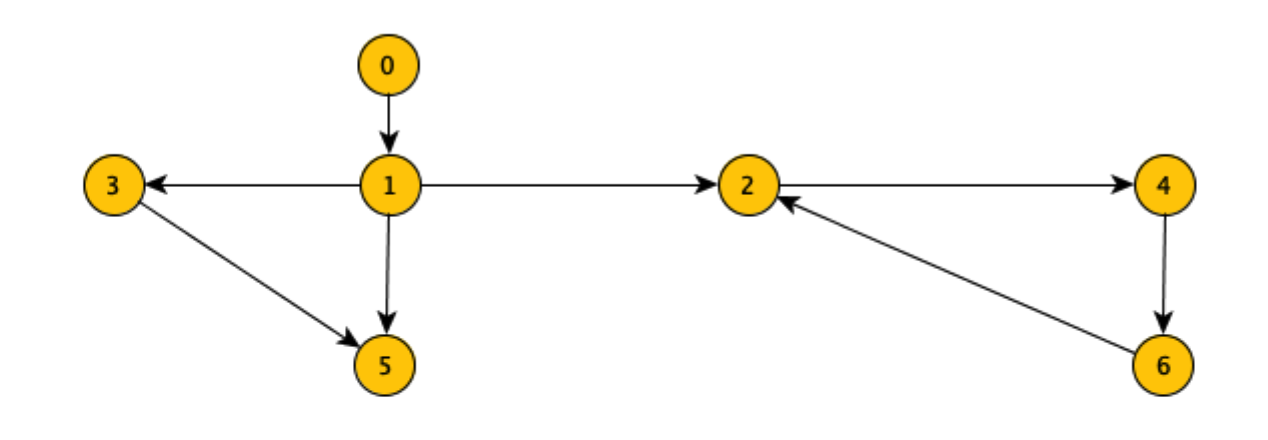
Raggiungibili da $(0, G) = {0, 1, 2, 3, 4, 5, 6}$
Raggiungibili da $(6, G) = {2, 4, 6}$
Raggiungibili da $(5, G) = {5}$

Visita tramite Matrice di Adiacenza

Possiamo usare il seguente algoritmo che ha un costo di $O (n^{2})$ , questo scorre in modo ricorsivo la matrice verso i valori che hanno valore 1 ovvero per quei nodi dove abbiamo un arco entrante da parte del nodo $v$

def DFS(u, M):
 
	def DFSr(u, M, visitati):
		visitati[u] = 1
		for i in range(len(M)):
			if M[u][i] == 1 and not visitati[i]:
				DFSr(i, M, visitati)
 
	n = len(M)
	visitati = [0] * n
	DFSr(u, M, visitati)
	return [x for x in range(n) if visitati[x]]

Visita tramite Liste di Adiacenza

Possiamo passare poi ad un algoritmo che ha costo $O (n + m)$ ma un costo di spazio di $O (n)$

def DFS(u, G):
 
	def DFSr(u, G, visitati):
		visitati[u] = 1
		for v in G[u]:
			if not visitati[v]:
				DFSr(v, G, visitati)
 
	n = len(G)
	visitati = [0] * n
	DFSr(u, G, visitati)
	return [x for x in range(n) if visitati[x]]

I costi sono dovuti al fatto che la creazione della lista visitati costa $Θ (n)$ mentre la funzione di ricerca costa $Θ (m)$ dato che stiamo pagando con il for un costo pari alla somma fra le cardinalità degli insiemi dei nodi adiacenti a ciascun nodo ovvero il numero totale degli archi $m$ . Quindi in totale $O (m + n)$ .

Per lo spazio è la lista visitati che occupa $n$ .

Da notare infatti che calcolare il grado di un nodo con la matrice ci costerà sempre $Θ (n)$ dato che dobbiamo sommare tutti i valori 1 presenti nella lista di quel nodo mentre per la lista di adiacenza ci costa $Θ (1)$ nella maggior parte dei casi e solo nel caso pessimo $Θ (n)$ infatti accediamo alla lista tramite il valore con costo 1 e poi calcoliamo la lunghezza della lista sempre con costo 1.

È possibile ovviamente avere anche una versione iterativa:

def DFS_iterativo(u,G):
	visitati = [0] * len(G)
	pila = [u]
	while pila:
		u = pila.pop()
		if not visitati[u]:
			visitati[u] = 1
			for v in G[u]:
				if not visitati[v]:
					pila.append(v)
	return [x for x in range(len(G)) if visitati[x]]

Questo inizializza la pila inserendo il nodo di partenza poi finché nella pila c’è qualcosa e questo non si trova nei nodi visitati allora lo inseriamo nei visitati rimuovendolo dalla pila e andiamo a controllare nella matrice alla lista corrispondente tutti i nodi collegati e li aggiungiamo alla pila.

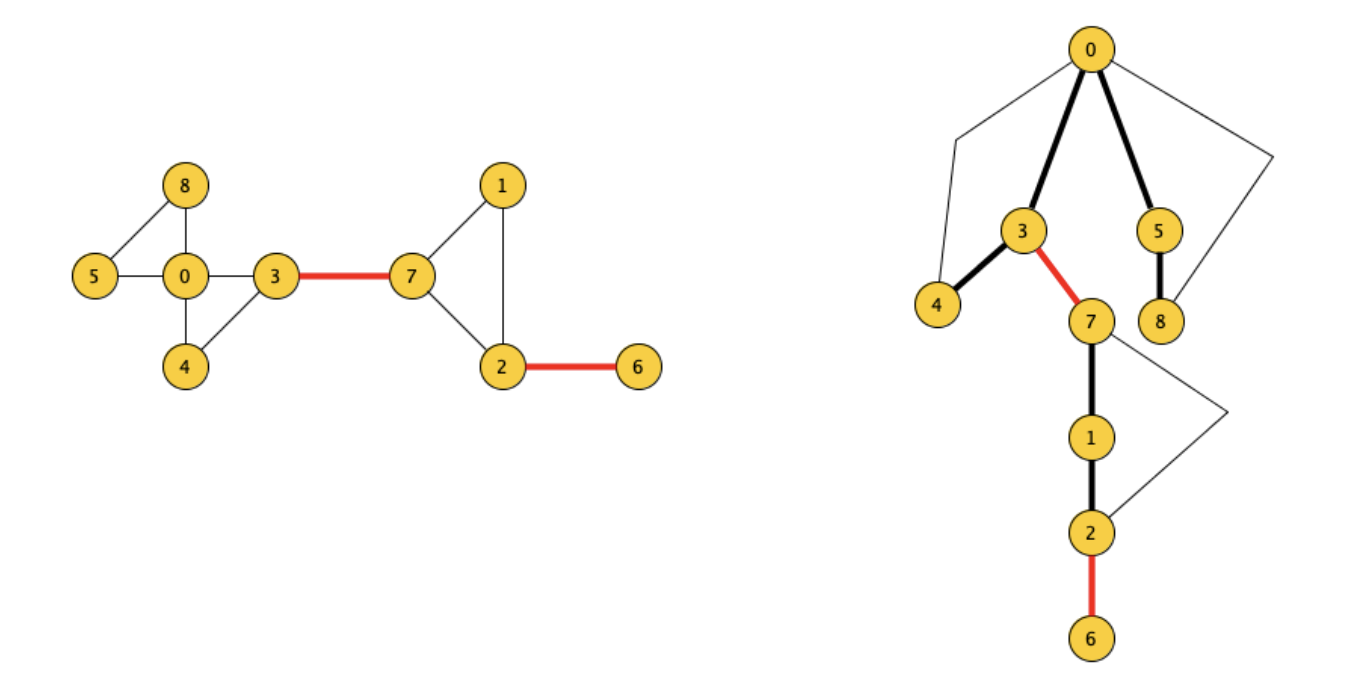
Con questo tipo di visite gli archi del grafo si bipartiscono in quelli percorsi dalla visita e quelli non, il percorso che effettuiamo andrà a creare un albero detto albero DFS.

Ad esempio prendiamo il grafo a sinistra ed eseguendo delle visite dai nodi 9, 4 e 3 otteniamo gli alberi accanto:

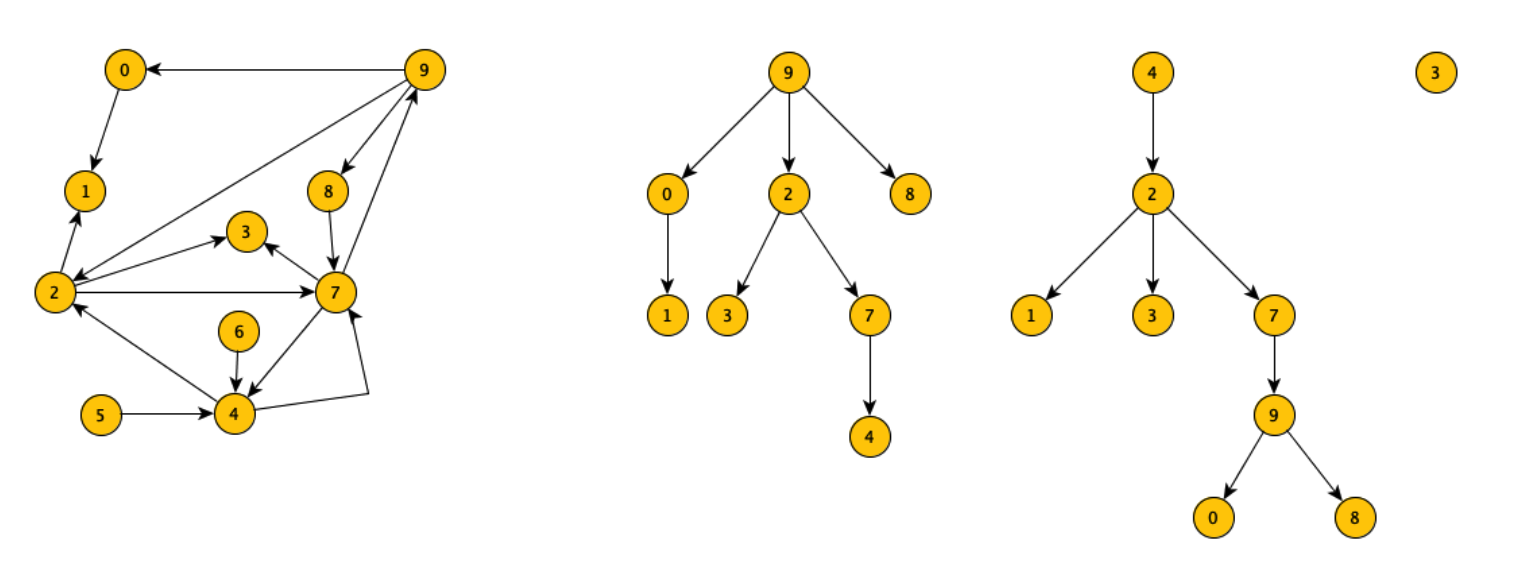
Un albero DFS può essere memorizzato tramite il vettore dei padri.

Vettore dei Padri

Il vettore dei padri $P$ di un albero DFS di un grafo di $n$ nodi ha $n$ componenti:

Se $i$ è nodo dell’albero DFS allora $P [i]$ contiene il padre del nodo $i$

Se $i$ non è nodo dell’albero allora $P [i]$ per convenzione contiene $- 1$

Esempi di rappresentazione con vettore dei padri

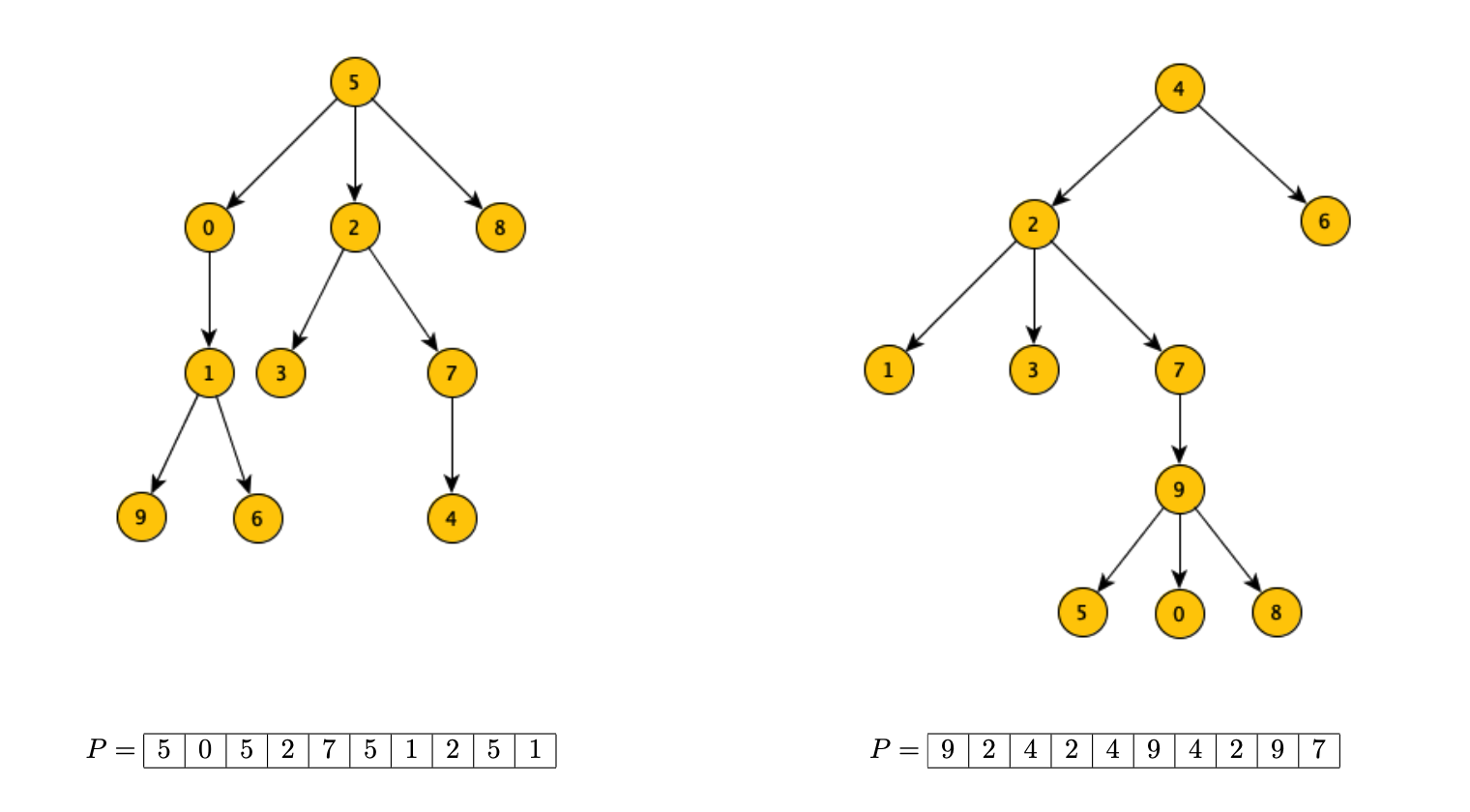
È possibile modificare l’algoritmo di visita DFS e fare in modo che restituisca il vettore dei padri radicato nel nodo da cui siamo partiti.

def Padri(u, G):
 
	def DFSr(x, G, P):
		for y in G[x]:
			if P[y] == -1:
				P[y] = x
				DFSr(y, G, P)
 
	n = len(G)
	P = [-1] * n
	P[u] = u
	DFSr(u,G,P)
	return P

Avremo che $P [v]$ contiene $- 1$ se $v$ non è stato visitato altrimenti contiene il padre di $v$ nell’albero DFS.

Percorsi diversi

Ovviamente in base all’ordinamento dei nodi all’interno delle liste le visite che faremo produrranno grafi e vettori dei padri diversi, ovvero se il nodo 2 ha come nodi adiacenti i nodi 3,4,5 a seconda di come troviamo questi nella lista otterremo diversi nodi. Infatti potremmo visitare prima 3 oppure 4 oppure 5.

Tramite il vettore dei padri possiamo trovare un percorso che ci porta dal nodo che abbiamo usato come radice fino al nodo scelto. Infatti se il nodo scelto non ha valore -1 nel vettore dei padri allora significa che è raggiungibile dalla radice, ci basta percorrere i padri dal vettore e poi invertire il percorso ottenuto ovvero il percorso foglia - radice.

Esempio

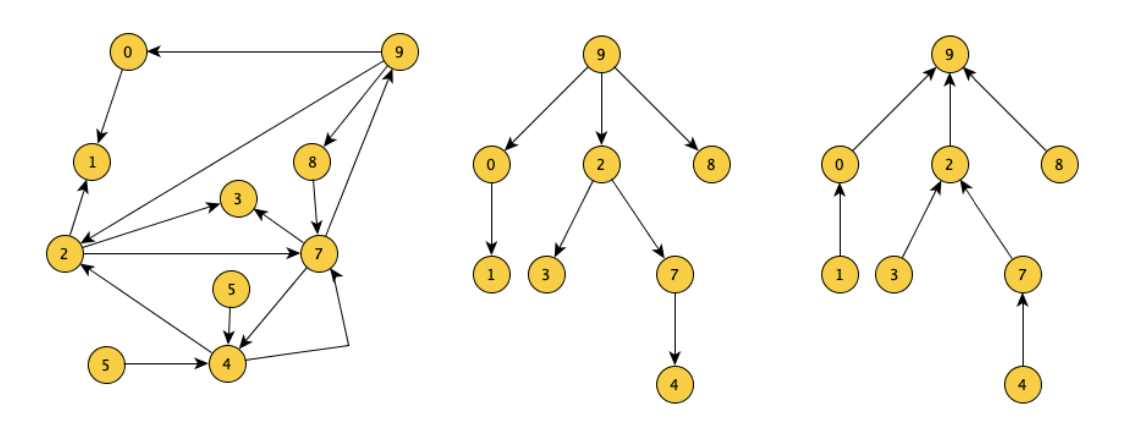
Il grafo a sinistra è quello originale e a destra abbiamo il grafo DFS che ha come radice 9.

Otteniamo come vettore dei padri:

Quindi ad esempio se cerchiamo un percorso per 5 e 6 non avremo risposta dato che questi non sono raggiungibili (hanno -1 come valore).

Per gli altri nodi invece seguiamo il percorso che ci indica il vettore, ad esempio:

7 → 2 → 9 Quindi come percorso abbiamo 9 - 2 - 7
1 → 0 → 9 Quindi otteniamo 9 - 0 - 1

Ovviamente questo non è garantito essere il percorso migliore.

Vediamo due procedura, una iterativa e una ricorsiva per trovare il percorso dato un vettore dei padri:

def Cammino(u, P):
	if P[u] == -1: return []
	path = []
	while P[u] != u:
		path.append(u)
		u = P[u]
	path.append(u)
	path.reverse()
	return path

def Cammino(u, P):
	if P[u] == -1: return []
	if P[u] == u: return [u]
	return CamminoR(P[u], P) + [u]

Sia la versione iterativa che quella ricorsiva hanno complessità di $O (n)$ se si dispone del vettore dei padri.

Colorazione di Grafi

Dato un grafo connesso un intero $k$ vogliamo sapere se è possibile colorare i nodi del grafo in modo che i nodi fra loro adiacenti abbiano sempre colori distinti.

Teorema 4 colori - Curiosità

Questo teorema afferma che un grafo planare richiede al più 4 colori per essere colorato. La dimostrazione è stata difficile da trovare anche perché doveva accontentare i matematici (🤓) che non si fidavano di una dimostrazione che sfruttava un calcolatore. Successivamente negli anni 2000 è stata proposta una dimostrazione che usa la teoria dei gruppi.

Nel peggiore dei casi ovvero un grafo completo, sono richiesti fino a $Θ (n)$ colori.

Per ora non esistono algoritmi che dato un grafo planare ci dicono se questo è 3-colorabile ma esistono invece degli algoritmi che ci dicono se un grafo è 2-colorabile.

Infatti un grafo è 2-colorabile se e solo se non contiene cicli di lunghezza dispari, infatti lungo il ciclo i colori devono alternarsi e arriveremo alla fine con gli ultimi due colori che si toccano.

Spiegazione algoritmo: Questo prova che un grafo senza cicli dispari può essere sempre 2-colorato:

Coloriamo il nodo 0 con il colore 0
Effettuiamo una visita in profondità a partire dal nodo 0 e ciascun nodo che incontriamo assegnamo uno dei due colori 0 o 1 in modo tale che questo sia diverso dal colore del nodo che ci ha portato a quello che stiamo colorando in quel momento.

Siano $x$ e $y$ due nodi adiacenti possono verificarsi due casi:

L’arco $(x, y)$ viene attraversato nella visita e quindi i nodi hanno colori distinti
L’arco $(x, y)$ non viene attraversato nella visita, allora sia $x$ il nodo visitato per primo esiste un cammino che ci porta da $x$ a $y$ che forma un ciclo con l’arco $(x, y)$ , questo ciclo è di lunghezza pari per ipotesi (abbiamo un grafo senza cicli dispari) quindi il cammino ha lunghezza dispari e questo significa che i colori su questo cammino si alterneranno.

Algoritmo per bicolorare grafi connessi senza cicli dispari:

def Colora(G):
 
	def DFSr(x, G, Colore, c):
		Colore[x] = c
		for y in G[x]:
			if Colore[y] == -1:
				DFSr(y, G, Colore, 1-c)
 
	Colore = [-1] * len(G)
	DFSr(0, G, Colore, 0)
	return Colore

Quindi inizializza una lista dei nodi con tutti valori -1 per indicare che non sono ancora colorati. Entra nel nodo 0 e lo colora con il colore 0 poi passa ai suoi adiacenti e li colora con 1, continua iterando in questo modo invertendo sempre il colore ad ogni nodo che attraversa.

Da notare che se il grafo contiene cicli dispari allora colorerà in modo errato. Ma questo si può perfezionare, infatti vediamo un algoritmo che in quel caso restituisce una lista vuota.

def Colora1(G):
 
	def DFSr(x, G, Colore, c):
		Colore[x] = c
		for y in G[x]:
			if Colore[y] == -1:
				if not DFSr(y, G, Colore, 1-c):
					return False
			elif Colore[y] == Colore[x]:
					return False
		return True
 
	Colore = [-1] * len(G)
	if DFSr(0, G, Colore, 0):
		return Colore
	return []

Quindi se non entriamo nei controlli aggiuntivi di adiacenza fra i colori che ci fanno ritornare False completeremo la costruzione della lista Colore altrimenti ne restituiremo una vuota.

La complessità è quella di una visita quindi $O (n + m)$ ma siccome abbiamo un grafo connesso e quindi $m \geq n - 1$ possiamo dire $O (m)$ .

Componente Connessa

Una componente connessa di un grafo è un sottografo composto da un insieme di nodi connessi con dei cammini. Un grafo si dice connesso se ha una sola componente connessa.

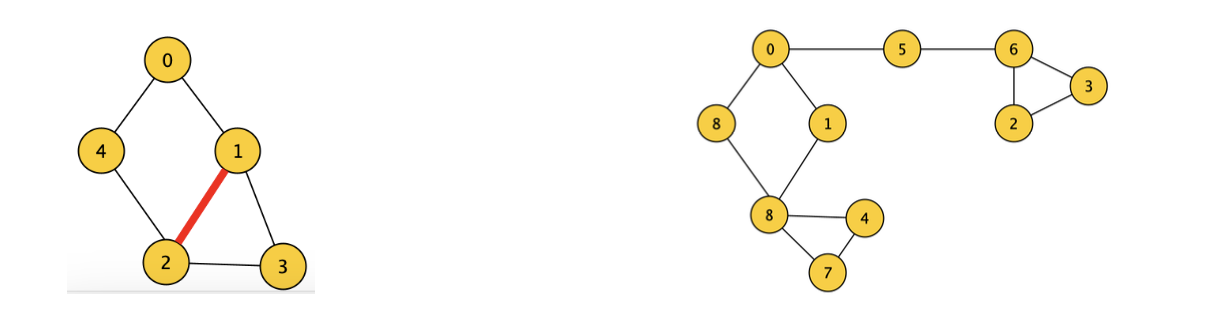
Esempio di grafo con più componenti connesse:

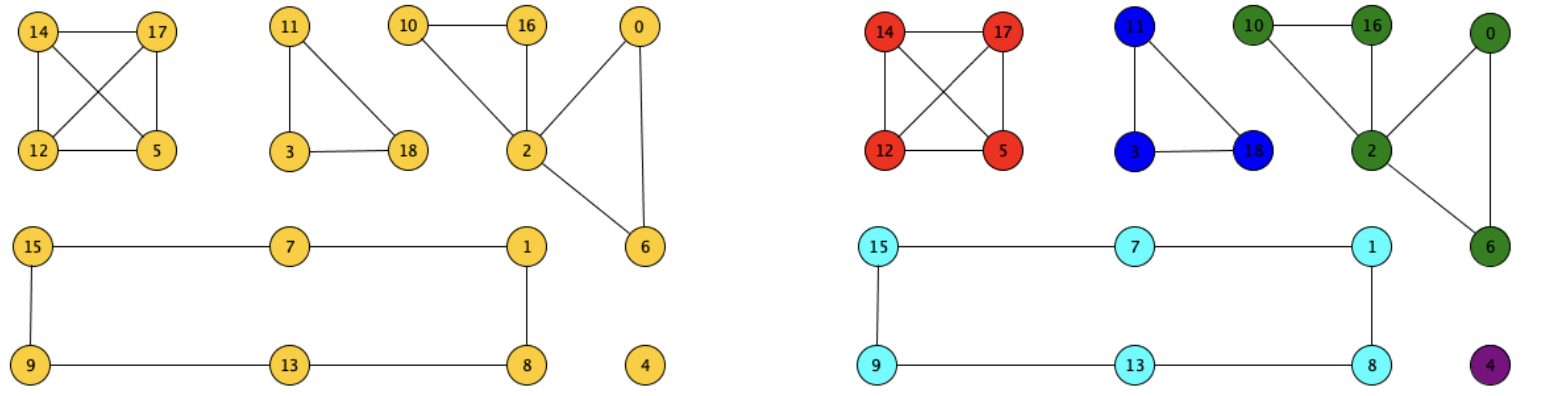
È possibile calcolare il vettore $C$ delle componenti connesse di un grafo, vale a dire un vettore che tanti elementi quanti i nodi del grafo e tale che se due nodi $x, y$ appartengono alla stessa componente allora $C [x] = C [y]$ , quindi se prendiamo come esempio il grafo sopra otteniamo:

$C = [2, 1, 2, 3, 4, 5, 2, 1, 1, 1, 2, 3, 5, 1, 5, 1, 2, 5, 3]$ (se non ho sbagliato qualche numero 🤡)

Nel vettore troveremo in totale $N$ valori in base a quante $N$ visite abbiamo fatto.

È possibile progettare un algoritmo che ci fa costruire questo vettore:

def Componenti(G):
 
	def DFSr(x, G, C, c):
		C[x] = c
		for y in G[x]:
			if C[y] == 0:
				DFSr(y, G, C, c)
 
	C = [0] * len(G)
	c = 0
	for x in range(len(G)):
		if C[x] == 0:
			c += 1
			DFSr(x, G, C, c)
	return C

Questo algoritmo scorre tutti i nodi nella liste di adiacenza, inizia con un valore $c = 1$ per il primo nodo e tutti quelli collegati a lui prenderanno il valore 1, quando non ci sarà più nessun nodo collegato a lui che ha valore 0 allora si passa al successivo nodo di un’altra componente (se esiste) aumentando il valore di $c$ di 1.

Componente Fortemente Connessa

Le componenti fortemente connesse, invece, le troviamo nei grafi diretti, queste sono dei sottografi composti da un insiemi di nodi connessi fra loro tramite dei cammini.

Anche in questo caso un grafo si dice fortemente connesso se ha una sola componente fortemente connessa.

Vogliamo trovare la componente fortemente connessa a partire da un nodo, in questo caso però l’algoritmo visto precedentemente non funziona questo perché se abbiamo un cammino da $x$ a $y$ non è detto che esista anche un cammino che da $y$ ci porta a $x$ .

Progettiamo l’algoritmo:

Calcolare l’insieme $A$ dei nodi di $G$ raggiungibili da $u$
Calcolare l’insieme $B$ dei nodi di $G$ che portano a $u$
Restituire l’intersezione di questi due insiemi

Per il passo 1 utilizziamo una semplice visita DFS quindi $O (n + m)$
Per il passo 2 ci serve il concetto di grafo trasposto
Il passo 3 costa $O (n)$

Grafo Trasposto

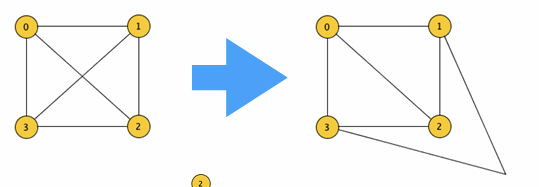
Dato un grafo diretto $G$ il grafo trasposto di $G$ denotato con $G^{T}$ ha gli stessi nodi di $G$ ma archi con direzione opposta, esempio:

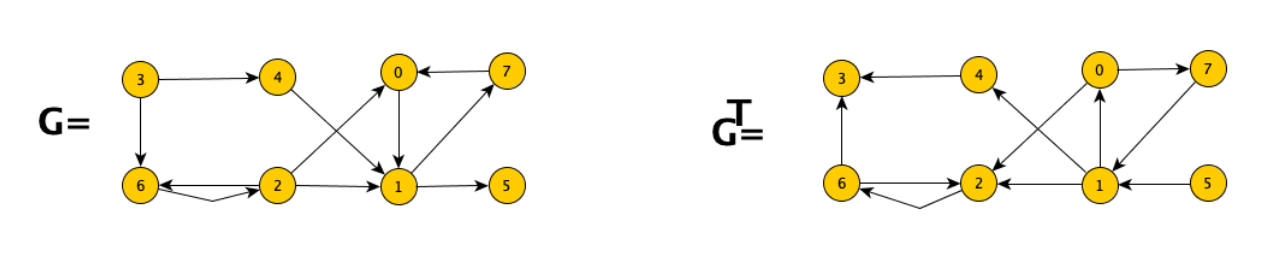
Quindi i nodi che in $G$ ci portano ad $u$ , in $G^{T}$ diventano i nodi che sono raggiungibili da $u$ .

Costruire questo grafo costa $O (n + m)$ .

In totale quindi abbiamo:

Passo 1 che costa $O (n + m)$ - Calcolare insieme $A$
Passo 2 che costa $O (n + m)$ - Calcolare grafo trasposto
Passo 3 che costa $O (n + m)$ - Calcolare insieme $B$ con una ricerca nel grafo trasposto
Passo 4, intersezione che costa $O (n)$

In totale $O (n + m)$

Vediamo un possibile algoritmo per costruire il vettore delle componenti fortemente connesse:

def ComponenteFC(x, G):
	visitati1 = DFS(x ,G)
	G1 = Trasposto(G)
	visitati2 = DFS(x, G1)
	componente = []
	for i in range(len(G)):
		if visitati1[i] == visitati2[i] == 1:
			componente.append(i)
	return componente
 
def Trasposto(G):
	GT = [[] for _ in G]
	for i in range(len(G)):
		for v in G[i]:
			GT[v].append(i)
	return GT

Se vogliamo ottenere il vettore delle componenti fortemente connesse possiamo usare l’algoritmo ComponenteFC come subroutine e ottenere:

def compFC(G):
	FC = [0] * len(G)
	c = 0
	for i in range(len(G)):
		if FC[i] == 0:
			E = ComponenteFC(i, G)
			c += 1
			for x in E:
				FC[x] = c
	return FC

Questo algoritmo ha complessità:

$Θ (n)$ per il for
$O (n + m)$ costo della funzione ComponenteFC

Quindi in totale $Θ (n) \cdot O (n + m) = O (n^{2} + nm) = O (n^{3})$ dato che al caso peggiore $O (m) = n^{2}$

Per verificare questo costo del caso peggiore possiamo pensare al grafo diretto $G$ avente un arco da $u$ a $v$ per ogni coppia di nodi $u, v$ tali che $u \leq v$

Questo grafo ha $n^{2}$ archi e $n$ componenti fortemente connesse ovvero una per ogni nodo, infatti:

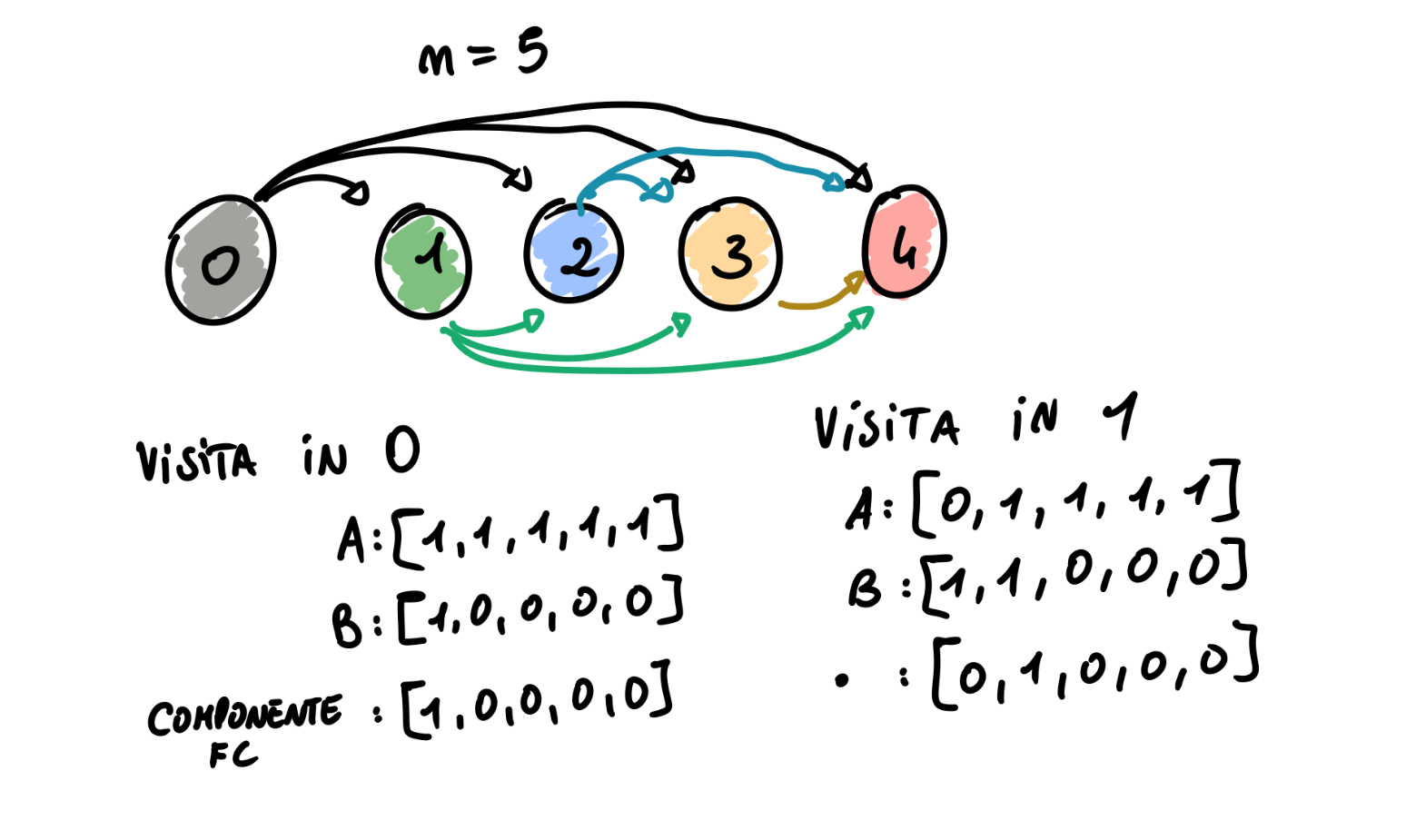
Ogni nodo equivale ad una componente connessa.

Ordinamento Topologico

Stesso concetto di Ordinamento Topologico

Spesso un grafo diretto cattura relazioni di propedeuticità fra i nodi, ovvero se ad esempio abbiamo un arco che va dal nodo $a$ al nodo $b$ allora $a$ è propedeutico a $b$ ovvero va svolto prima di $b$ .

In un grafo è possibile rispettare tutte le propedeuticità se riusciamo ad ordinare i nodi del grafo in modo che gli archi vadano tutti da sinistra verso destra, questo è detto ordinamento topologico.

Un grafo può avere da $0$ a $n!$ ordinamenti topologici

Esempio

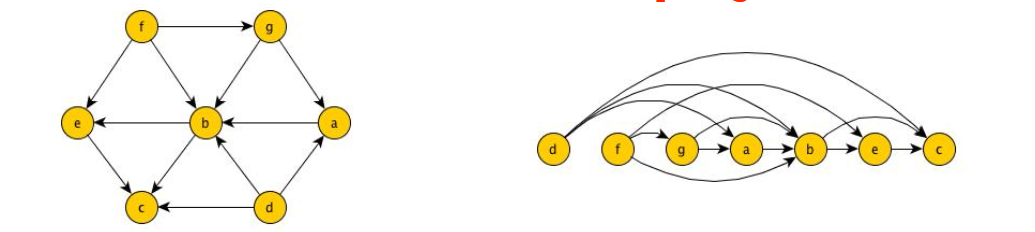
Tentare tutte le combinazioni di un grafo e vedere se sono un ordinamento topologico costa troppo, ovvero $Ω (n!)$ . Possiamo però fare delle osservazioni.

Affinché $G$ possa avere un ordinamento topologico è necessario che sia un DAG ovvero un Grafo Diretto Aciclico. Infatti se abbiamo un ciclo è impossibile avere tutte le frecce in una sola direzione, una andrà sicuramente nella direzione opposta.

Possiamo dimostrare che questa condizione, ovvero essere DAG è anche sufficiente per far si che esista un ordinamento topologico.

Un DAG ha sempre un nodo sorgente ovvero un nodo in cui non entrano archi, possiamo sfruttare questo per costruire l’ordinamento:

Iniziamo da una sorgente
Cancelliamo questa sorgente dal grafo e gli archi che partono da lui ottenendo così un nuovo DAG
Iteriamo in questo modo finché non abbiamo ordinato tutti i nodi

Un possibile algoritmo è il seguente:

def sortTop(G):
 
    n = len(G)
    gradoEnt = [0] * n 
    for i in range(n): 
        for j in G[i]:
            gradoEnt[j] += 1 # posso fare len(G[i]) senza for ?? 
    sorgenti = [ i for i in range(len(G)) if gradoEnt[i] == 0 ]
    ST = []
    
    while sorgenti:
        u=sorgenti.pop()
        ST.append(u)
        for v in G[u]:
            gradoEnt[v] -= 1
            if gradoEnt[v] == 0:
                sorgenti.append(v)
                
    if len(ST)==len(G): return ST
    return []

Se esiste un ordinamento questo viene restituito altrimenti viene restituita una lista vuota.

Spiegazione

Con il primo for creiamo un array che per ogni nodo ha assegnato un valore uguale a quanti archi entranti ha quel nodo. Questo ci costa $O (m)$ , insieme all’inizializzazione del vettore che ha costo $Θ (n)$ abbiamo un costo totale di $O (m + n)$
Creiamo l’array sorgenti prendendo quei nodi che hanno valore 0 nell’array precedente ovvero che non hanno archi entranti. Costo di $O (n)$
Con il while andiamo a creare l’ordinamento vero e proprio, finché ci sono delle sorgenti ne togliamo una e la inseriamo nell’ordinamento, a questo punto riduciamo di uno il grado di tutti i nodi collegati a questa sorgente e controlliamo se ci sono nuove sorgenti da aggiungere. Nel caso peggiore controlliamo tutto il grafo e quindi abbiamo un costo di $O (m)$
Infine controlliamo se l’ordinamento comprende tutti i nodi, se si ne abbiamo trovato uno altrimenti restituiamo una lista vuota.

Analizzando meglio i costi abbiamo:

Inizializzazione vettore dei gradi ovvero la creazione vera e propria e l’assegnamento dei valori - $O (n + m)$
Creazione vettore delle sorgenti - $O (n)$
Il ciclo while itera $O (n)$ volte ma il for al suo interno, nel caso peggiore, scorre tutto il grafo come detto prima, quindi $O (m)$
Costo totale di $O (n + m)$

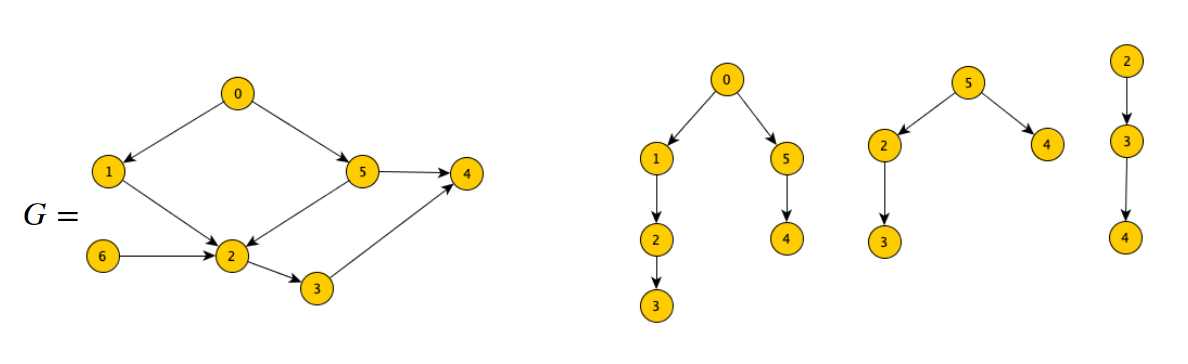
Possiamo usare un algoritmo alternativo che si basa sulla DFS, questa DFS però inserirà i nodi in una lista soltanto quando la visita su questi sarà terminata, l’algoritmo restituisce il reverse della lista. Questa DFS va effettuata su tutti i nodi a partire dal nodo 0.

Esempio

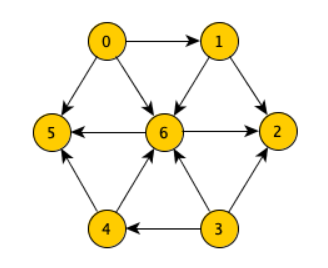
In questo caso se effettuiamo una visita sul nodo 0 otteniamo:

$[2, 5, 6, 1, 0, 4, 3]$ Perché siamo partiti dal nodo 0 e una volta terminato abbiamo continuato ad effettuare visite sui nodi rimanente ovvero 3 e 4. Ovviamente non viene restituita quella lista ma il suo inverso, quindi $[3, 4, 0, 1, 6, 5, 2]$ .

Perché funziona? - Siano $x$ e $y$ due nodi in $G$ con un arco che va da $x$ a $y$ dimostriamo i possibili casi:

Se l’arco viene attraversato durante la visita allora $y$ finirà nella lista prima di $x$ e quindi facendo il reverse otteniamo un giusto ordinamento
Se l’arco non viene attraversato allora significa che durante la visita di $x$ il nodo $y$ è già stato visitato e la sua visita è anche già terminata dato che da $y$ non può esserci un cammino che ci porta ad $x$ altrimenti non avremmo un DAG. Anche in questo caso quindi $y$ finisce nella lista prima di $x$ .

Implementiamo l’algoritmo:

def sortTop1(G):
 
	def DFSr(u, G, visitati, lista):
		visitati[u] = 1
		for v in G[u]:
			if visitati[v] == 0:
				DFSr(v, G, visitati, lista)
		lista.append(u)
 
	visitati = [0] * len(G)
	lista = []
	for u in range(len(G)):
		if visitati[u] == 0:
			DFSr(u, G, visitati, lista)
	lista.reverse()
	return lista

Che ha una complessità di $O (n + m) + O (n) = O (n + m)$

Grafo Parzialmente Orientato

Un grafo $G$ si dice parzialmente orientato se contiene sia archi orientati che archi non orientati

Cicli

Dato un grafo $G$ diretto o non diretto ed un suo nodo $u$ vogliamo sapere se da $u$ è possibile raggiungere un ciclo in $G$ .

Esempio

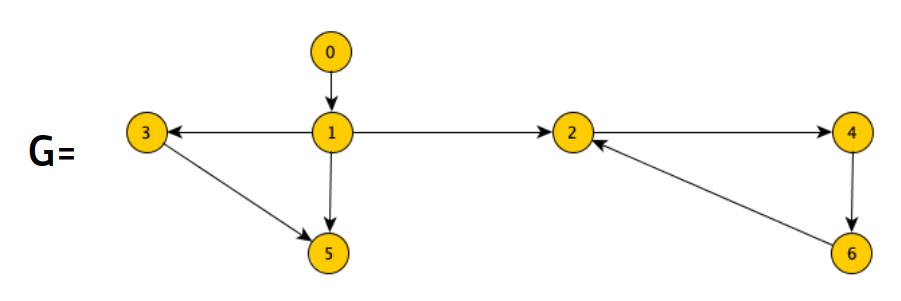
Da questo grafo se partiamo dal nodo 1 possiamo raggiungere un ciclo ad esempio 2,4,6. Mentre se partiamo dal nodo 3 non è possibile raggiungere un ciclo dato che possiamo arrivare soltanto al nodo 5.

Una prima idea è quella di visitare il grafo e se durante la visita incontriamo un nodo già visto allora la interrompiamo e restituiamo True altrimenti se la visita viene portata a termina restituiamo False. Ma questa idea è sbagliata nel caso di grafi non diretti infatti se $x, y$ sono due nodi collegati allora appariranno ciascuno nella lista di adiacenza dell’altro e questo viene interpretato come un ciclo di lunghezza 2 facendo terminare il nostro algoritmo sempre con True.

Per risolvere questo problema devo distinguere per ciascun nodo $y$ che incontro, il nodo $x$ che mi ha portato a visitarlo, quindi:

def ciclo(u, G):
	visitati = [0] * len(G)
	return DFSr(u, u, G, visitati)
 
def DFSr(u, padre, G, visitati):
	visitati[u] = 1
	for v in G[u]:
		if visitati[v] == 1:
			if v != padre:
				return True
		else:
			if DFSr(v, u, G, visitati):
				return True
	return False

Che ha una complessità di $O (n)$ perché se il grafo non contiene cicli allora ha al più $n - 1$ archi e quindi $O (n + m) = O (n)$ . Se invece contiene cicli ne scopriamo uno dopo aver considerato al più $n$ e l’algoritmo termina.

Anche nel caso di grafi diretti l’algoritmo non è corretto perché incontrare un nodo già visitato in un grafo diretto non significa necessariamente che ci sia un ciclo, quindi la procedura potrebbe terminare con True anche in assenza di cicli

Durante la visita DFS posso incontrare nodi già visitati in tre modi diversi:

archi in avanti ovvero le frecce che da un antenato puntano ad un discendente
archi all’indietro ovvero le frecce che da un discendente vanno ad un antenato
archi di attraversamento ovvero quelle frecce che ci portano da un sottoalbero ad un altro

Esempi

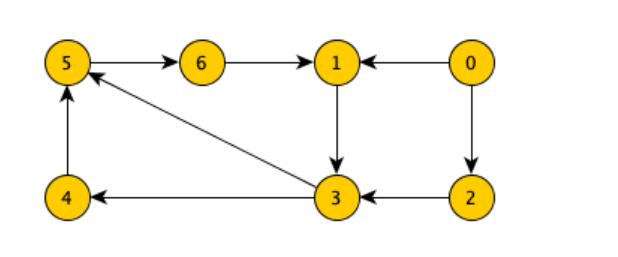
Che effettuando una visita DFS a partire da 0 otteniamo:

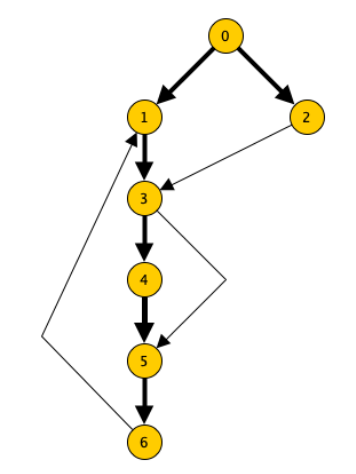
In questa ricerca finiamo in un nodo già visitato in 3 casi:

3 → 5 questo è un arco in avanti dato che 3 è antenato di 5
6 → 1 arco indietro perché 1 e antenato di 6
2 → 3 è di attraversamento dato che ci porta in un altro sottoalbero (o comunque non è ne avanti ne indietro)

Soltanto la presenza di archi all’indietro testimonia la presenza di un ciclo. Dobbiamo quindi distinguere la scoperta di nodi già visitati grazie ad un arco all’indietro rispetto agli altri tipi di archi.

Possiamo individuarli notando che soltanto nel caso di archi all’indietro andiamo a visitare un nodo già visitato ma che non ha ancora finito la sua ricorsione, ad esempio nel grafo sopra abbiamo 6 che ci porta ad 1, un nodo già visitato e 1 non ha ancora finito la sua ricorsione.

Progettiamo un algoritmo per il vettore V dei visitati:

In V un nodo vale 0 se il nodo non è stato ancora visitato
In V un nodo vale 1 se il nodo è stato visitato ma la ricorsione su quel nodo non è ancora finita
In V un nodo vale 2 se il nodo è stato visitato e ha terminato la sua ricorsione

In questo modo se troviamo un arco diretto verso un nodo che ha valore 1 abbiamo trovato un ciclo.

def DFSr(u, G, visitati):
	visitati[u] = 1
	for v in G[u]:
		if visitati[v] == 1:
			return True
		if visitati[v] == 0:
			if DFSr(v, G, visitati):
				return True
	visitati[u] = 2
	return False
 
def cicloD(u, G):
	visitati = [0] * len(G)
	return DFSr(u, G, visitati)

Questo algoritmo ha complessità $O (n + m)$ e restituisce True se è presente un ciclo, False altrimenti.

Se vogliamo sapere se c’è un ciclo o no in un grafo diretto o non diretto possiamo modificare la procedura in questo modo:

def cicloD(G):
	visitati = [0] * len(G)
	for u in range(len(G)):
		if visitati[u] == 0:
			if DFSr(u, G, visitati):
				return True
	return False

Che si basa sempre su impostare i valori nel vettore a 0,1,2 come stabilito prima.

Ponti

La connessione in un grafo può essere persa con la perdita di un arco, se un arco viene eliminato e la sua eliminazione porta alla disconnessione del grafo allora l’arco prende il nome di ponte.

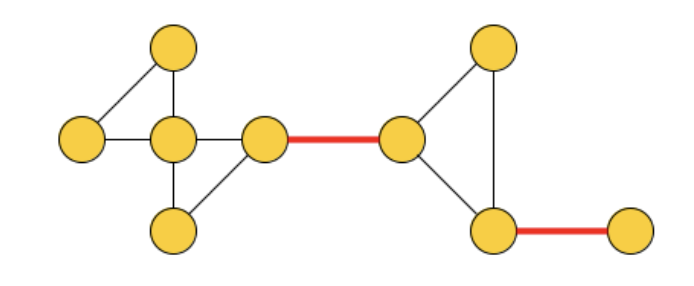
È importante quindi trovare i ponti dato che rappresentano delle criticità del grafo.

Come determiniamo l’insieme dei ponti in un grafo?

Iniziamo facendo due osservazioni:

Se come grafo abbiamo un ciclo allora non abbiamo ponti
Se come grafo abbiamo un albero allora qualsiasi nodo sarà un ponte

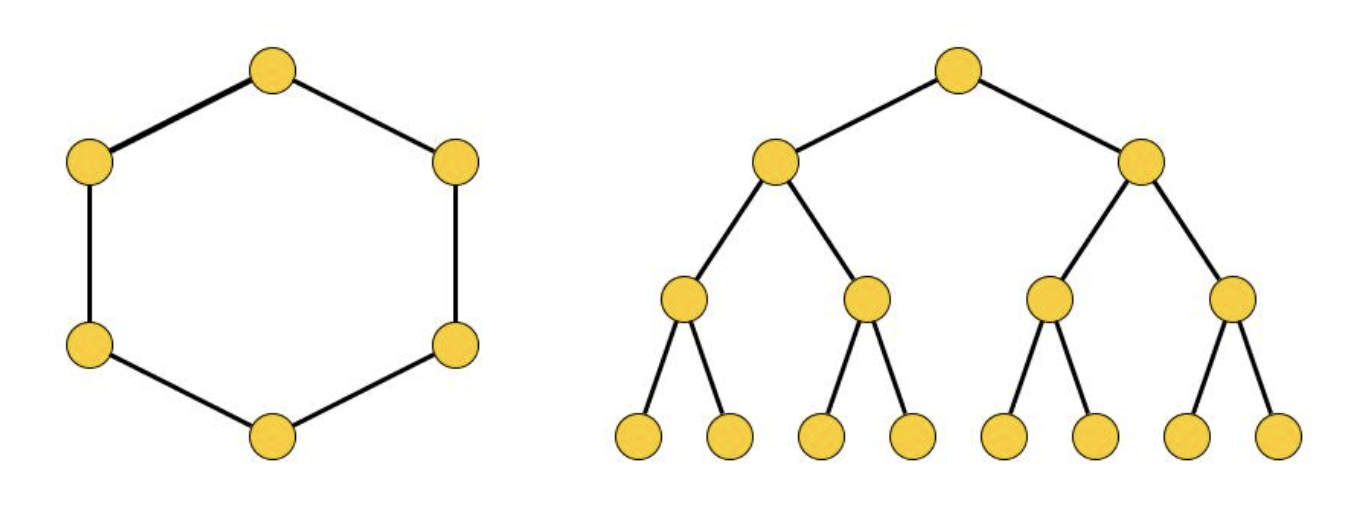
La prima soluzione potrebbe essere una ricerca esaustiva quindi per ogni arco provare ad eliminarlo e vedere se il grafo ottenuto è connesso o no ma la complessità di questo algoritmo risulterebbe $O (n^{4})$ .

Modificando però una DFS possiamo raggiungere una complessità di $O (m)$ .

I ponti vanno ricercati unicamente tra gli $n - 1$ archi dell’albero DFS, infatti se un arco non è presente nell’albero DFS significa che se lo elimino allora gli archi dell’albero DFS continuano ad essere connessi.

Ma come riconosciamo un ponte?

Se prendiamo ${u, v}$ un arco dell’albero DFS con $u$ padre e $v$ figlio, l’arco è un ponte se e solo se non ci sono altri archi tra i nodi del sottoalbero radicato in $v$ e il nodo $u$ o antenati di $u$ .

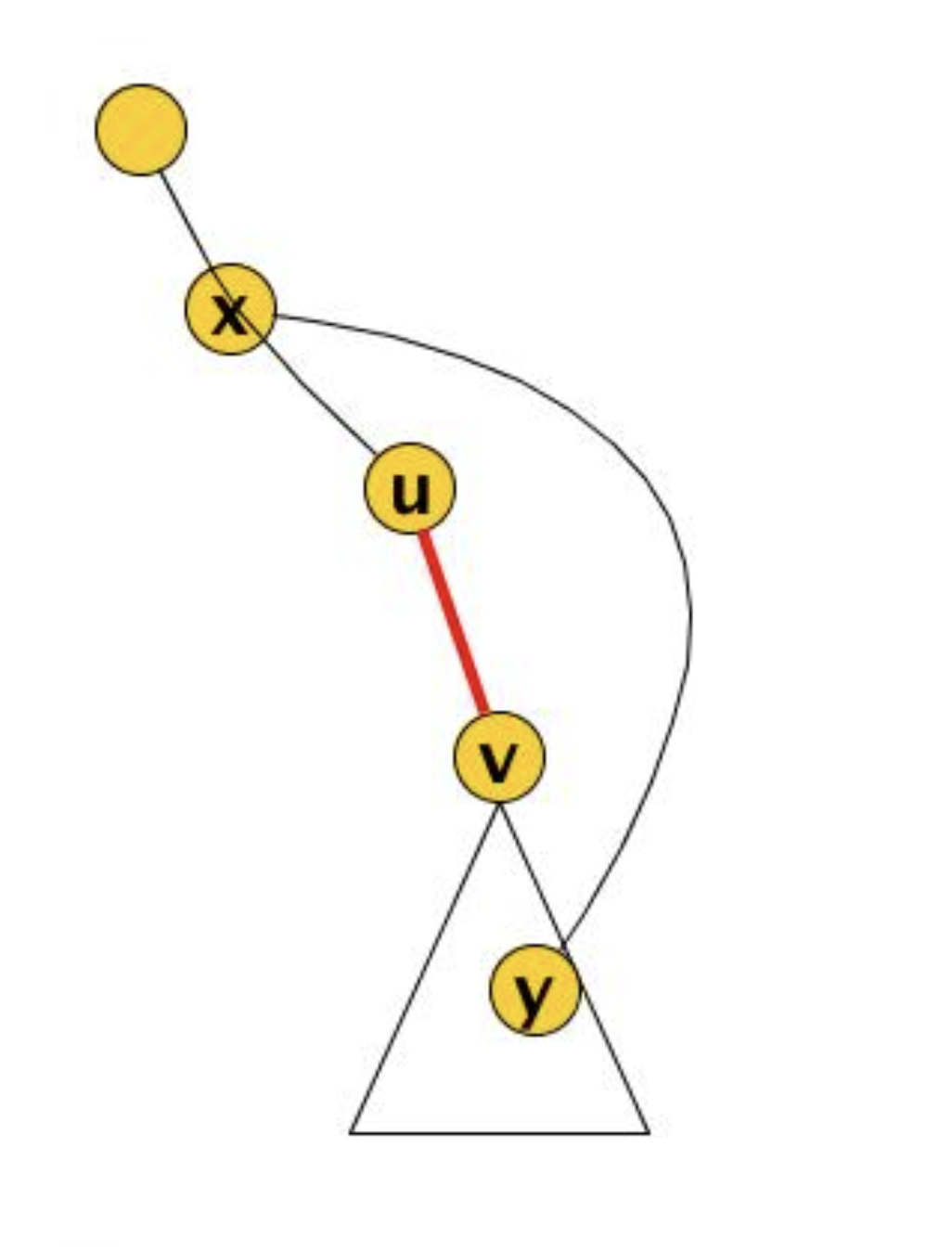
Infatti cancellare l’arco $u - v$ in questo grafo non lo disconnette, abbiamo l’arco $x - y$ che ci “protegge”, dove $x$ è discendente di $v$ e $x$ è antenato di $u$ . Se non fosse esistito questo arco allora l’eliminazione dell’arco $u - v$ avrebbe portato alla disconnessione del sottoalbero radicato in $v$ dato che tutti gli archi del sottoalbero sarebbero nati e terminati nel sottoalbero.

Per costruire un algoritmo possiamo notare che quando attraversiamo $u - v$ per raggiungere $v$ , il nodo $u$ non può sapere se ci saranno archi che portano a suoi antenati ma può scoprirlo successivamente se $v$ una volta terminata la sua ricerca gli restituisce le giuste informazioni.

Quindi, per ogni arco padre - figlio $(u, v)$ presente nell’albero DFS il nodo $u$ è in grado di scoprire se l’arco $(u, v)$ è ponte o meno usando questa strategia:

Ogni nodo $v$
- Calcola la sua altezza nell’albero
- Calcola e restituisce al padre l’altezza minima che si può raggiungere con archi che partono dai nodi del suo sottoalbero diversi dall’arco $(u, v)$

A questo punto il padre $u$ confronta l’altezza ricevuta dal figlio con la sua altezza, se l’arco è un ponte deve accadere che l’altezza del padre deve essere minore di quella ricevuta dal figlio che significa appunto che dal figlio non possiamo raggiungere un nodo precedente al padre nell’albero DFS.

Esempi

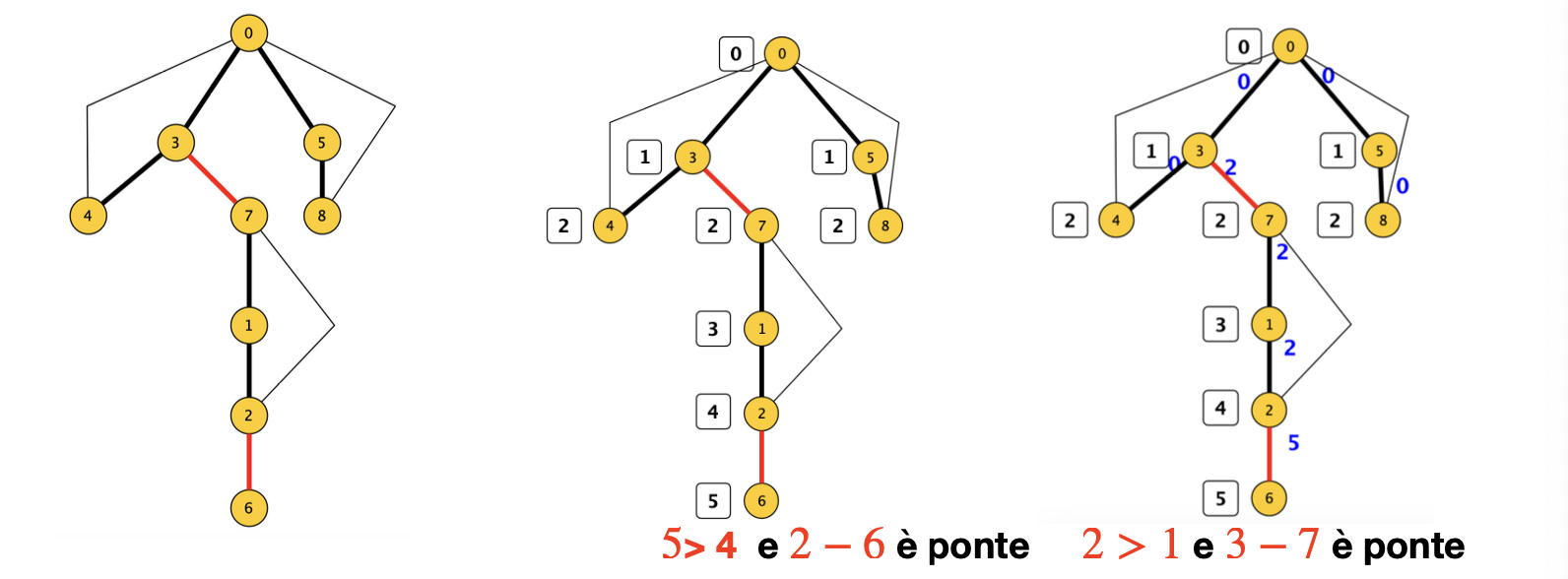
Ricordiamo di non dover considerare l’arco stesso per il calcolo dell’altezza minima da restituire.

Possibile Implementazione:

def trova_ponti(G):
    """ Trova tutti i ponti in un grafo connesso non orientato G.
    G è rappresentato come una lista di adiacenza.
    Restituisce una lista di coppie (u, v) che sono ponti.
    """
 
    ####
 
    def dfs(x, padre, altezza, ponti):
        # Assegna l'altezza al nodo corrente
        if padre == -1:
            altezza[x]=0
        else:
            altezza[x] = altezza[padre] + 1
        # Minima altezza raggiungibile dal sottoalbero di x
        min_raggiungibile = altezza[x]
        for y in G[x]:
            if altezza[y] == -1:
                # il nodo y non è stato ancora visitato
                b = dfs(y, x, altezza, ponti)
                if b > altezza[x]:
                    # l'altezza di x è minore di quella ritornata da y,
                    # quindi (x, y) è un ponte
                    ponti.append((x, y))
                min_raggiungibile = min(min_raggiungibile, b)
            elif y != padre:
                # y già visitato e (x,y) è un arco all'indietro
                min_raggiungibile = min(min_raggiungibile, altezza[y])
        return min_raggiungibile
 
    # Array per memorizzare l'altezza dei nodi nella DFS
    altezza = [-1] * len(G)
    ponti = []
    # Inizia la DFS dal nodo 0
    dfs(0, -1, altezza, ponti)
    return ponti

Come detto prima abbiamo il costo di una ricerca e quindi $O (n + m)$

Punto di Articolazione

Un punto di articolazione è un vertice la cui rimozione è in grado di sconnettere il grafo

Grafo Cactus

Un grafo cactus è un grafo connesso non orientato in cui ogni arco appartiene al massimo ad un ciclo, ad esempio:

Il grafo a sinistra non è un cactus dato che l’arco $1 - 2$ appartiene a due cicli. Il grafo a destra invece è un cactus dato che non ci sono archi in comune fra cicli.

La Visita in Ampiezza BFS

Dati due nodi $a$ e $b$ di un grafo $G$ definiamo distanza minima in $G$ di $a$ da $b$ il numero minimo di archi che bisogna attraversare per raggiungere $b$ a partire da $a$ , per convenzione poniamo la distanza a $+ \infty$ se $b$ non è raggiungibile.

Adesso dato un grafo $G$ ed un suo nodo $x$ vogliamo conoscere le distanze di tutti i nodi di $G$ da $x$ , vogliamo quindi calcolare il vettore delle distanze $D$ dove in $D [y]$ troviamo la distanza di $y$ da $x$ .

Con la visita in ampiezza esploriamo i nodi del grafo partendo da quelli a distanza 1 dalla sorgenti poi a quelli a distanza 2 e così via. In questo modo generiamo un albero chiamato albero BFS.

Per fare questa visita manteniamo in una coda i nodi visitati i cui adiacenti non sono ancora stati esplorati, ad ogni passo preleviamo dalla coda ed esaminiamo i suoi adiacenti, se scopriamo un nuovo nodo lo visitiamo e lo aggiungiamo alla coda.

Vediamo l’implementazione:

def BFS(x, G):
	visitati = [0] * len(G)
	visitati[x] = 1
	coda = [x]
	while coda:
		u = coda.pop(0)
		for y in G[u]:
			if visitati[y] == 0:
				visitati[y] = 1
				coda.append(y)
	return visitati

A fine algoritmo avremo che visitati[u] contiene 1 soltanto se da $x$ possiamo raggiungere $u$ .

Per quanto riguarda la complessità abbiamo che un nodo finisce nella coda al più una volta quindi il while viene eseguito $O (n)$ volte.

Le liste di adiacenza dei nodi verranno scorse al più una volta quindi il costo totale dei for sarà $O (m)$

In totale quindi se le operazioni sulla coda hanno costo 1 abbiamo $O (n + m)$ però abbiamo la coda tramite una lista dove inseriamo in coda e cancelliamo in testa, quindi:

Inserimento costa 1
Estrazione costa in base a quanti elementi ci sono nella coda che possono essere anche $O (n)$

Come costo totale otteniamo quindi $O (n^{2})$

Possiamo notare questo costo un esempio:

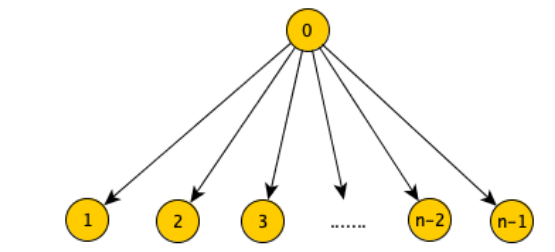
In questo caso, partiamo da 0 ed inseriamo tutti i nodi nella coda, ad ogni for ne estraiamo uno e alla prima iterazione paghiamo $n - 1$ , alla seconda $n - 2$ e così via.

Possiamo fare delle modifiche e ottenere una ricerca con costo $O (n + m)$ .

È possibile farlo se nella coda invece di eliminare gli elementi usiamo un puntatore che incrementiamo di volta in volta:

def BFS(x, G):
	visitati = [0] * len(G)
	visitati[x] = 1
	coda = [x]
	i = 0
	while len(coda) > i:
		u = coda[i]
		i += 1
		for y in G[u]:
			if visitati[y] == 0:
				visitati[y] = 1
				coda.append(y)
	return visitati

In Python è possibile farlo anche tramite la struttura deque.

Adesso modifichiamo questa ricerca per fare in modo che restituisca il vettore dei padri

def BFSpadri(x, G):
	P = [-1] * len(G)
	P[x] = x
	coda = [x]
	i = 0
	while len(coda) > i:
		u = coda[i]
		i += 1
		for y in G[u]:
			if P[y] == -1:
				P[y] = u
				coda.append(y)
	return P

Proprietà

La distanza minima di un vertice $x$ da $s$ nel grafo $G$ equivale alla profondità di $x$ nell’albero BFS. È grazie a questa proprietà che l’albero BFS è anche detto albero dei cammini minimi

Modifichiamo ulteriormente l’algoritmo per fare in modo che restituisca il vettore delle distanze $D$ :

def BFSdistanza(x, G):
	D = [-1] * len(G)
	D[x] = 0
	coda = [x]
	i = 0
	while len(coda) > i:
		u = coda[i]
		i += 1
		for y in G[u]:
			if D[y] == -1:
				D[y] = D[u] + 1
				coda.append(y)
	return D

Se in un nodo abbiamo come valore $- 1$ allora significa che non abbiamo raggiunto quel nodo.

👨🏻‍💻 Alem's Notes

Grafi

Grafi tramite Matrici Binarie

Trovare un Pozzo

Grafi tramite Liste di Adiacenza

In generale chi e quando scegliere?

Visite nei Grafi

Visita tramite Matrice di Adiacenza

Visita tramite Liste di Adiacenza

Colorazione di Grafi

Componente Connessa

Componente Fortemente Connessa

Grafo Trasposto

Ordinamento Topologico

Cicli

Ponti

La Visita in Ampiezza BFS

Table of Contents

Backlinks