Le strutture dati servono ad organizzare ed accedere ai dati in modo organizzato, queste sono composte da:

Un modo di organizzare i dati
Degli operatori che permettono la manipolazione della struttura

Inoltre possono essere:

omogenee o disomogenee rispetto ai dati contenuti, quindi se contengono o no dati dello stesso tipo
Statiche o dinamiche a seconda che possano o meno cambiare la loro dimensione

Struttura Statica

Una struttura dati statica è una struttura in cui la dimensione è fissa e deve essere specificata al momento della creazione, queste spesso sono più efficienti in termini di spazio e accesso.

Struttura Dinamica

Una struttura dinamica invece ha una dimensione che può variare durante l’esecuzione del programma, sono quindi utili quando la dimensione della struttura è incerta.

Cosa scegliere quindi?

Ovviamente dipende dalle nostre esigenze e dalle operazioni previste sulla struttura, le strutture dinamiche offrono una maggiore flessibilità ma possono richiedere più memoria e potrebbero avere prestazioni peggiori mentre una struttura statica è meno flessibile ma più efficiente se conosciamo la lunghezza necessaria.

Gli elementi di una struttura dinamica sono chiamati record e possono contenere più di un dato elementare, per questo è molto comune che questi abbiano:

Chiave: utilizzata per distinguere un elemento da un altro
Dati Satellite: Ulteriori dati relativi all’elemento ma non utilizzati nelle operazioni di manipolazione perché non ci permettono di distinguere gli elementi fra loro.

In alcuni casi però la chiave coincide con l’elemento stesso e non contiene altri dati.

Operazioni di Interrogazione

Queste non modificano l’insieme ma ci restituiscono determinati valori:

Search(S,x): Recupera l’elemento con chiave x se è presente in S
Min(S): Restituisce il minimo valore presente in S
Max(S): Restituisce il massimo valore presente in S

Operazioni di Manipolazione

Queste invece modificano il nostro insieme:

Insert(S,x): Inserisce l’elemento x in S
Delete(S,x): Elimina da S l’elemento x

Vettore

In questa struttura il numero degli elementi è fissato, quindi è un insieme statico, gli elementi sono posti in memoria in successione e organizzata tramite indici, quindi l’accesso ad un elemento è diretto. Vediamo i costi delle operazioni viste prima svolte su un vettore ordinato o non:

Liste Semplici con Puntatori

In questa struttura gli elementi sono collegati fra loro tramite dei puntatori, è possibile accedere alla lista da una delle due estremità e poi scorrerla tramite questi. Infatti ogni elemento contiene un puntatore al successivo e quindi possiamo effettuare soltanto un accesso sequenziale agli elementi, non diretto.

Quindi a differenza dei vettori il costo di accesso ad un elemento è direttamente proporzionale alla sua posizione e quindi nel caso peggiore dell’ultimo elemento presente è $θ (n)$

Quindi nello specifico, ogni elemento di lista è un record a due campi:

una chiave che contiene l’informazione vera e propria
un campo next che contiene il puntatore alla locazione di memoria dell’elemento successivo, nel caso dell’ultimo elemento la lista contiene un apposito valore None

Posizione in memoria dei record

A differenza dei vettori quindi, dove gli elementi si trovano in successione nella memoria, nelle liste puntate gli elementi possono trovarsi anche in locazioni molto distanti fra loro.

In Python possiamo creare una nuova classe Nodo per aiutarci a organizzare una lista puntata:

class Nodo:
	def __init__(self, key = None, next = None):
		self.key = key
		self.next = next

Possiamo quindi generare dei nodi e concatenarli fra loro:

lista = Nodo(4)
lista.next = Nodo(9)
lista.next.next = Nodo(7)
# [4,9,7]
# Se cambiamo l'accesso al primo elemento:
lista = lista.next
# [9,7]

Dobbiamo prestare attenzione ai puntatori che indicano a locazioni di memoria, infatti se un dato non è puntato da nessuno questo verrà restituito al sistema e lo perderemo, se vogliamo quindi spostarci di indice nella lista ma non perdere il suo inizio, conviene creare una nuova variabile che punti a quel dato.

Creazione di una Lista Puntata

Creiamo una funzione che dato in input un Array A crea la corrispondente lista puntata, termina restituendo l’inizio della lista

def Crea(A):
	if A == []:
		return None
	p = Nodo(A[0])
	q = p # Puntatore per non perdere l'inizio
	for i in range(1, len(A)):
		q.next(A[i])
		q = q.next
	return p

Il costo computazionale è pari a $θ (n)$

Stampa di una Lista Puntata

Funzione che prende in input il puntatore p che punta alla testa della lista e stampa i contenuti di ciascun nodo

def Stampa(p):
	while p:
		print(p.key)
		p = p.next

Il costo computazionale è pari a $θ (n)$

Ricerca nelle Liste Puntate

La funzione dato in input un puntatore alla testa della lista e un valore x da cercare restituisce il puntatore al primo nodo della lista che contiene x altrimenti None

def Ricerca(p, x):
	q = p
	while q != None and q.key != x:
		q = q.next
	return q

Il costo computazionale è pari a $O (n)$

Inserimento nelle Liste Puntate

La funzione, dato il puntatore alla testa e il valore x da inserire, inserisce l’elemento alla testa e restituisce il nuovo puntatore

def Inserisci(p, x):
	q = Nodo(x, p)
	return q

Il costo computazionale è pari a $θ (1)$

Inserimento dopo alcuni valori

Possiamo effettuare l’inserimento, ad esempio, dopo un certo valore y

def inserisci1(p, x, y):
	while p != None and p.key != y:
		p = p.next
	if p != None:
		p.next = Nodo(x, p.next)

Il costo computazionale è pari a $O (n)$

Eliminazione nelle Liste Puntate

La funzione dato il puntatore alla testa un valore x cancella dalla lista la prima occorrenza e restituisce il nuovo puntatore.

def Cancella(p, x):
	if p != None:
		if p.key == x:
			p = p.next
		else:
			q = p
			while q.next != None and q.next.key != x:
				q = q.next
			if q.next != None:
				q.next = q.next.next
	return p

Il costo computazionale è pari a $O (n)$

Ricordiamo che per cancellare un nodo è sufficiente renderlo inaccessibile ad esempio impostandolo a None ma non devono esserci nemmeno altri puntatori che lo referenziano, altrimenti il sistema non lo cancellerà dalla memoria.

Liste Doppiamente Puntate

Possiamo riorganizzare la struttura in modo che da ogni suo elemento si possa accedere si all’elemento successivo che al precedente.

class NodoD:
	def __init__(self, key = None, prev = None, next = None):
		self.key = key
		self.prev = prec
		self.next = next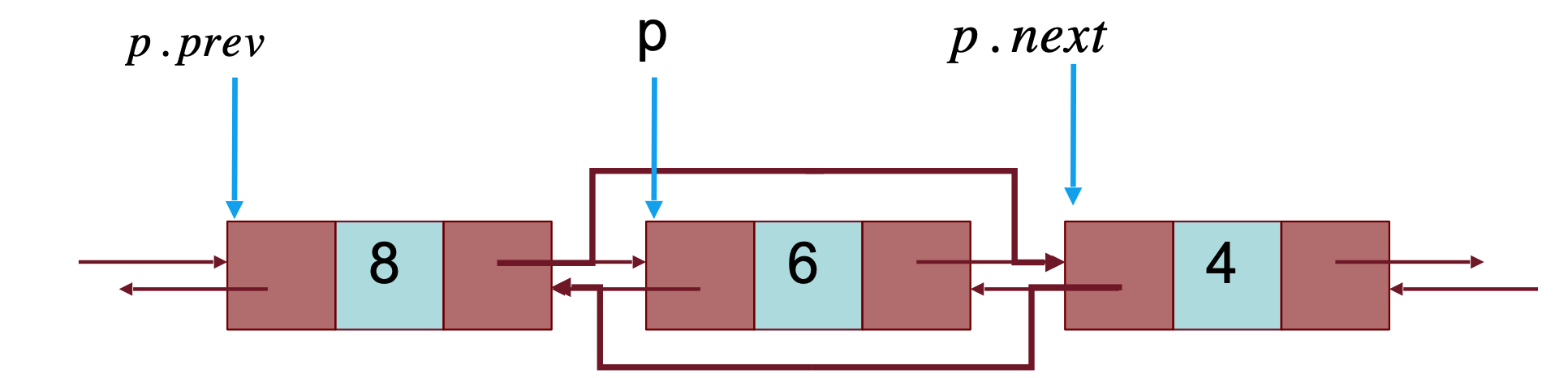

Creazione

def creaDoppia(A):
	if A == []:
		return None
	p = Nodo(A[0])
	q = p
	for i in range(1, len(A)):
		q.next = NodoD(A[i], q)
		q = q.next
	return p

Il costo computazionale è pari a $O (n)$

Per cancellare un elemento dalla memoria dobbiamo quindi, togliere entrambi i riferimenti

p.prev.next = p.next
p.next.prev = p.prev

Pila

La pila è una struttura dati con un comportamento LIFO (Last In First Out) quindi l’ultimo elemento ad entrare è il primo ad uscire. Un esempio è lo stack utilizzato per le chiamate di sistema.

Su una pila sono definite le operazioni di Push (Inserimento) e Pop (Estrazione), la particolarità della pila deriva dal fatto che push e pop lavorano alla stessa estremità attraverso un puntatore.

Vediamo un’implementazione attraverso le liste

def push(Pila, x):
	Pila.append(x)
 
def pop(Pila):
	if Pila = []:
		return None
	return Pila.pop()

Quindi possiamo notare che entrambe le operazioni hanno costo computazionale pari a $θ (1)$

Implementazione con Liste Puntate - Push

La funzione Push riceve il puntatore alla cima della lista ed il valore x da inserire, lo inserisce in un nodo in cima alla lista puntata e restituisce il nuovo puntatore

def push(top, x):
	return Nodo(x, top)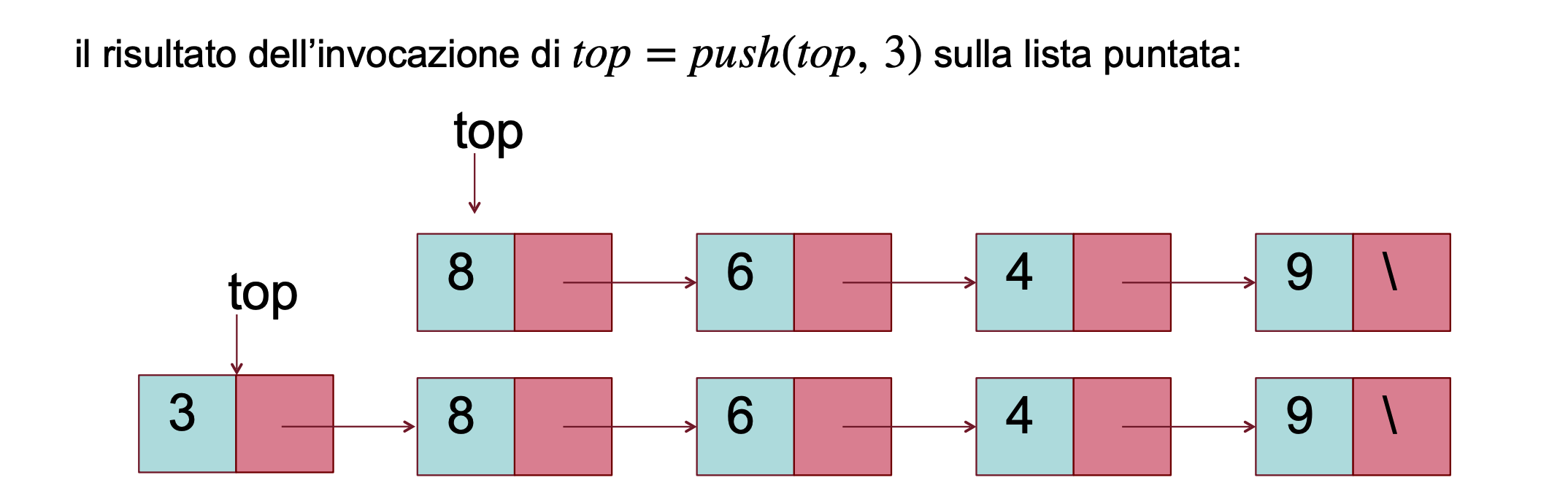

Implementazione con Liste Puntate - Estrazione

La funzione Pop prende il puntatore alla cima della pila e restituisce il valore del nodo in cima alla pila insieme alla nuova cima.

def pop(top):
	if top == None:
		return None, None
	return top.key, top.next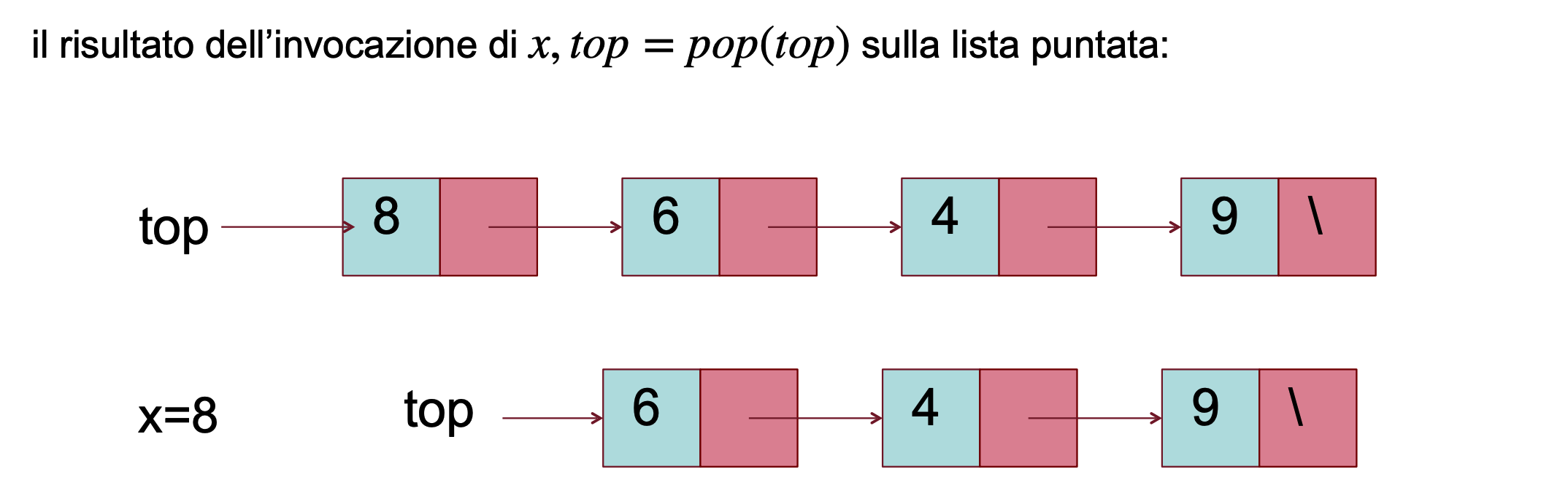

Coda

La coda è una struttura dati con funzionamento FIFO (First In First Out) quindi il primo elemento ad entrare è il primo ad uscire.

Le operazione di inserimento e estrazione vengono chiamate rispettivamente Enqueue e Dequeue e quindi la particolarità della coda è che la Enqueue opera sulla coda tail della coda e la Dequeue sulla testa head.

Implementazione attraverso le liste

def inserisci(Coda, x):
	Coda.append(x)
 
def estrai(Coda):
	if Coda = []:
		return None
	return Coda.pop(0)

Notiamo che per l’inserimento abbiamo un costo pari a $θ (1)$ mentre per l’estrazione $θ (n)$ dato che dobbiamo far slittare tutti gli elementi rimanenti

Implementazione con Liste Puntate - Enqueue

La funzione Enqueue prende in input i puntatori di testa e coda ed il valore da inserire, restituisce i nuovi puntatori

def enqueue(testa, coda, x):
	p = Nodo(x)
	if coda == None:
		return p, p
	coda.next = p
	return testa, p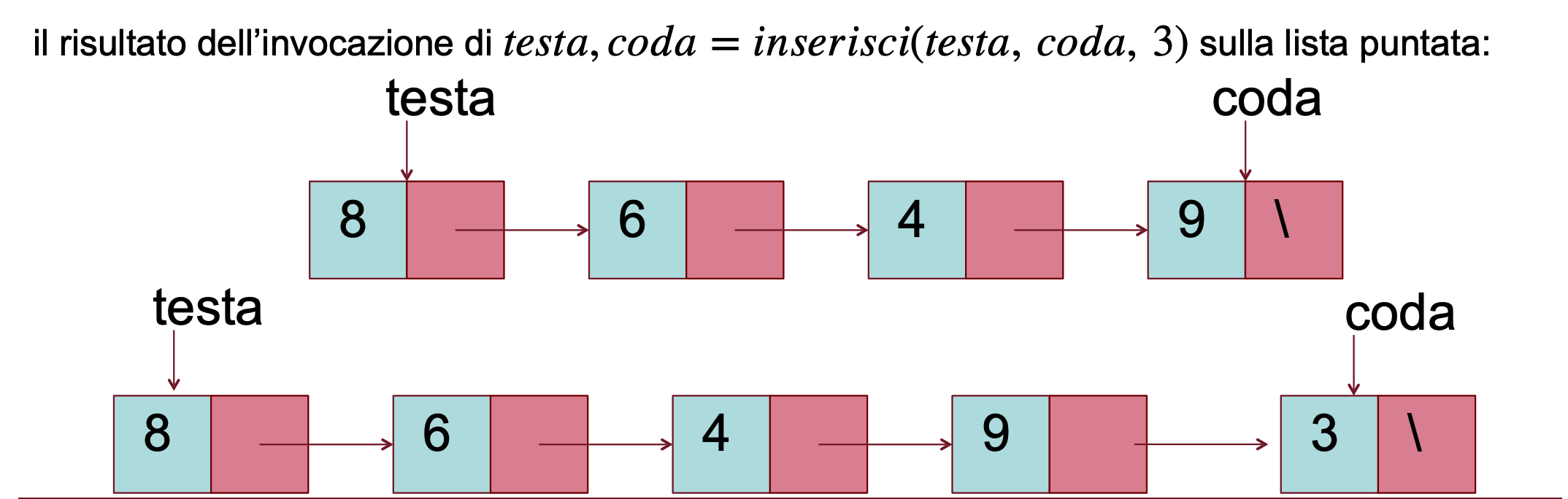

Implementazione con Liste Puntate - Dequeue

La funzione dequeue prende in input i puntatori di testa e coda, estrae il valore dalla testa e restituisce valore e nuovi puntatori

def dequeue(testa, coda):
	if testa == None:
		return None, None, None
	if testa == coda:
		return testa.key, None, None
	return testa.key, testa.next, coda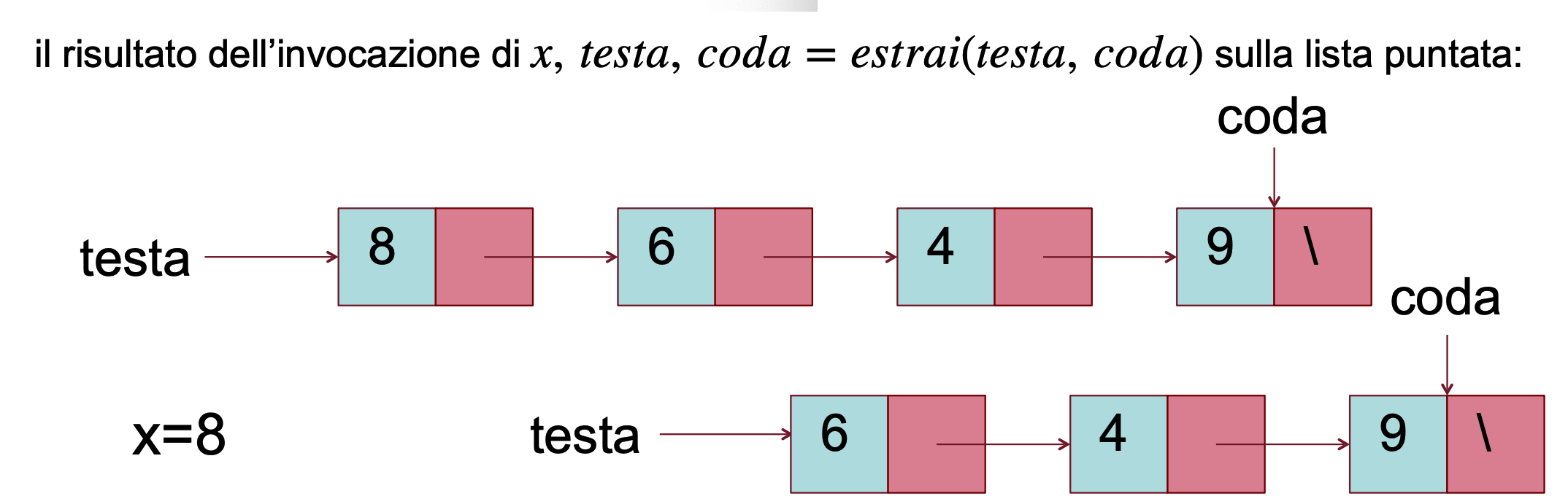

Code con priorità

La coda con priorità è una variante della coda, ha le stesse caratteristiche di inserimento ed estrazione ma la posizione di ogni elemento non dipende dal momento in cui è stato inserito ma dal valore di una determinata grandezza detta priorità

Alberi

L’albero è una struttura dati, esistono diversi tipi di alberi.

Alberi Radicati

In un albero radicato i nodi sono organizzati in livelli numerati in ordine crescente partendo dalla radice che è il livello 0. L’altezza è il cammino più lungo che possiamo fare dalla radice a una foglia dell’albero, quindi un albero di altezza $h$ contiene $h + 1$ livelli perché numerati da $0$ a $h$ .

Definizioni

Dato un nodo $v$ , esclusa la radice, il primo nodo che incontriamo andando verso la radice si chiama padre di $v$ .
Nodi che hanno lo stesso padre si dicono fratelli
La radice non ha padre
Ogni nodo sul cammino da $v$ alla radice viene detto antenato di $v$
Tutti i nodi che ammettono $v$ come padre sono detti figli di $v$
I nodi che non hanno figli sono detti foglie
Tutti i nodi che ammettono $v$ come antenato sono detti discendenti di $v$

Esempio Grafico

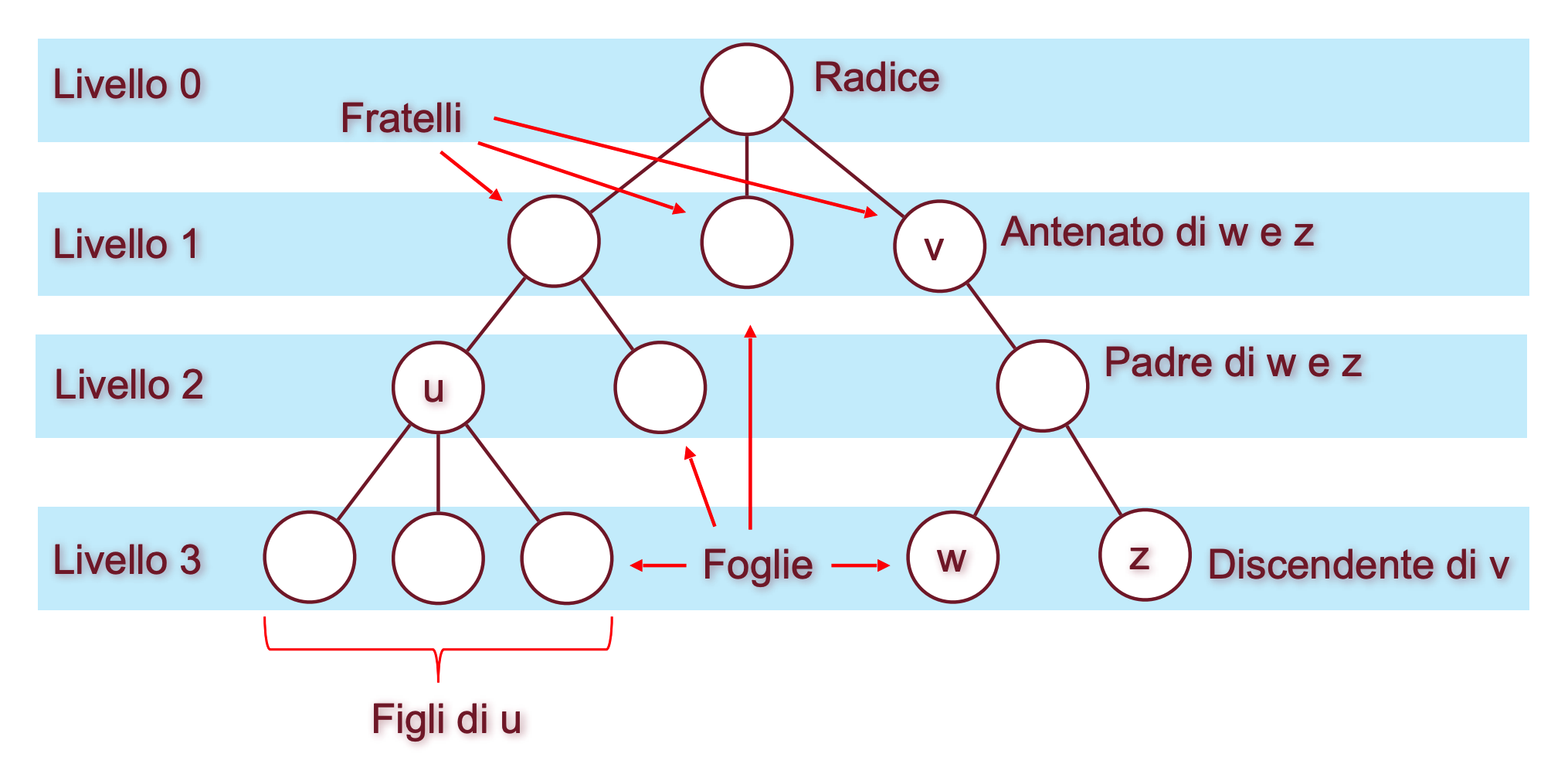
Albero Radicato Ordinato

Un albero radicato si dice ordinato quando ai figli è stato attribuito un ordine, quindi possiamo identificare un primo, secondo, terzo, k-esimo figlio.

Una sottoclasse degli alberi radicati infatti sono gli alberi binari dove ogni nodo ha al più due figli e siccome sono ordinati possiamo identificare figlio sinistro e figlio destro.

Alberi Binari

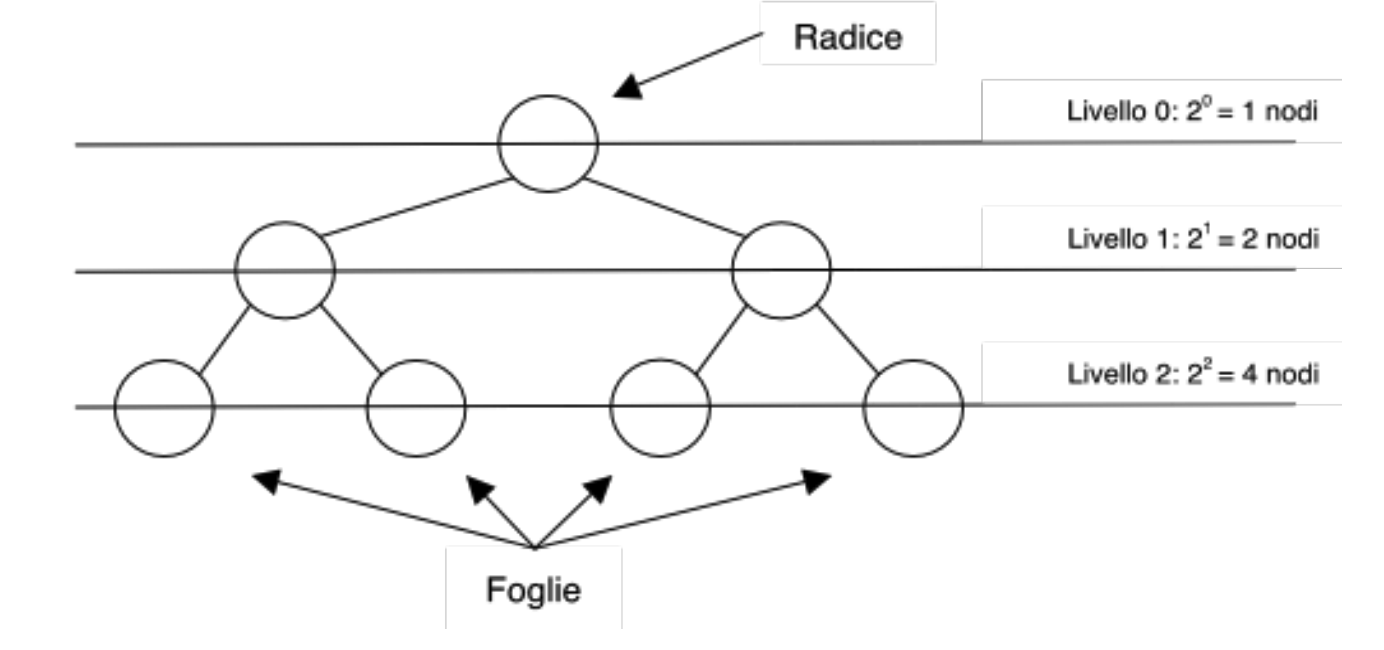
Un albero binario dove ogni livello contiene il numero massimo di nodi si dice completo, se invece tutti i livelli contengono il numero massimo di nodi eccetto l’ultimo, l’albero è detto quasi completo.

Quindi in un albero binario completo abbiamo che:

Il numero delle foglie è $2^{h}$
Il numero dei nodi interni è $i = 0 \sum h - 1 2^{i} = 2^{h} - 1$
Il numero totale dei nodi è $2^{h + 1} - 1$

Esempio con h = 2

Quindi in un albero binario completo possiamo calcolare l’altezza $h$ :

Il numero dei nodi è $n = 2^{h + 1} - 1 \to n + 1 = 2^{h + 1}$
Quindi $lo g_{2} (n + 1) = h + 1$
$h = lo g_{2} (n + 1) - 1 = lo g_{2} \frac{n + 1}{2}$

Quindi per un albero binario completo otteniamo che $h = θ (lo g n)$ mentre per un albero binario generico $h = Ω (lo g n)$

Rappresentazione di un Albero Binario in Memoria

Esistono 3 diversi metodi per rappresentare un albero binario nella memoria

Memorizzazione tramite Record e Puntatori

In questo metodo ogni nodo è costituito da un record che contiene

key: il valore del nodo
left: il puntatore al figlio sinistro o None se non presente
right: il puntatore al figlio destro o None se non presente Accediamo all’albero tramite il nodo della radice

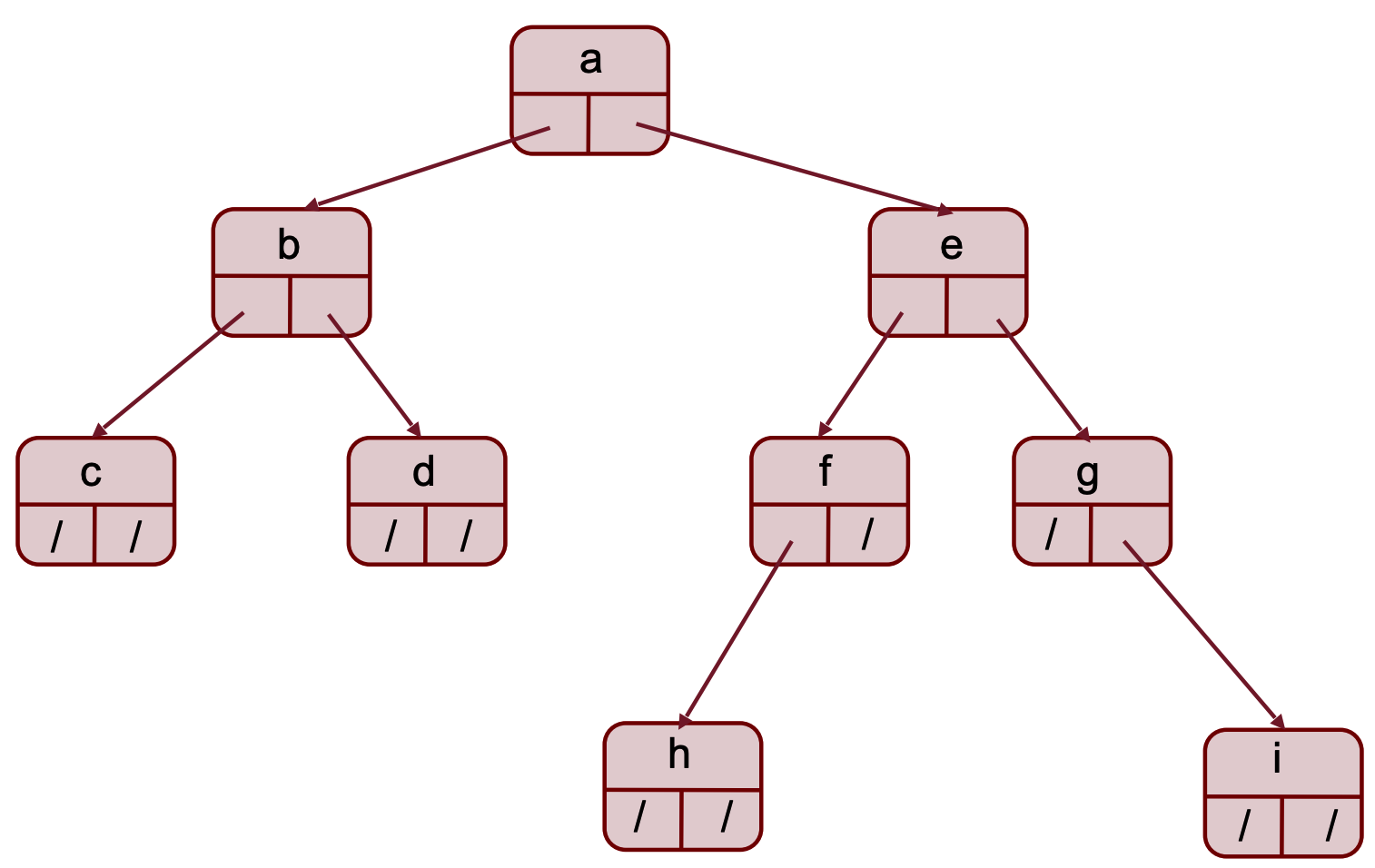
Rappresentazione Posizionale

È lo stesso metodo usato per rappresentare la heap come una lista, quindi la radice occupa la posizione 0 ed i figli sinistro e destro del nodo in posizione $i$ si trovano rispettivamente nelle posizioni $2 i + 1, 2 i + 2$ . Lo svantaggio di questa rappresentazione è che in ogni caso avremo bisogno di un vettore in grado di contenere un albero completo di altezza $h$ e se l’albero non è molto denso di elementi si verifica uno spreco di spazio

Esempio Grafico

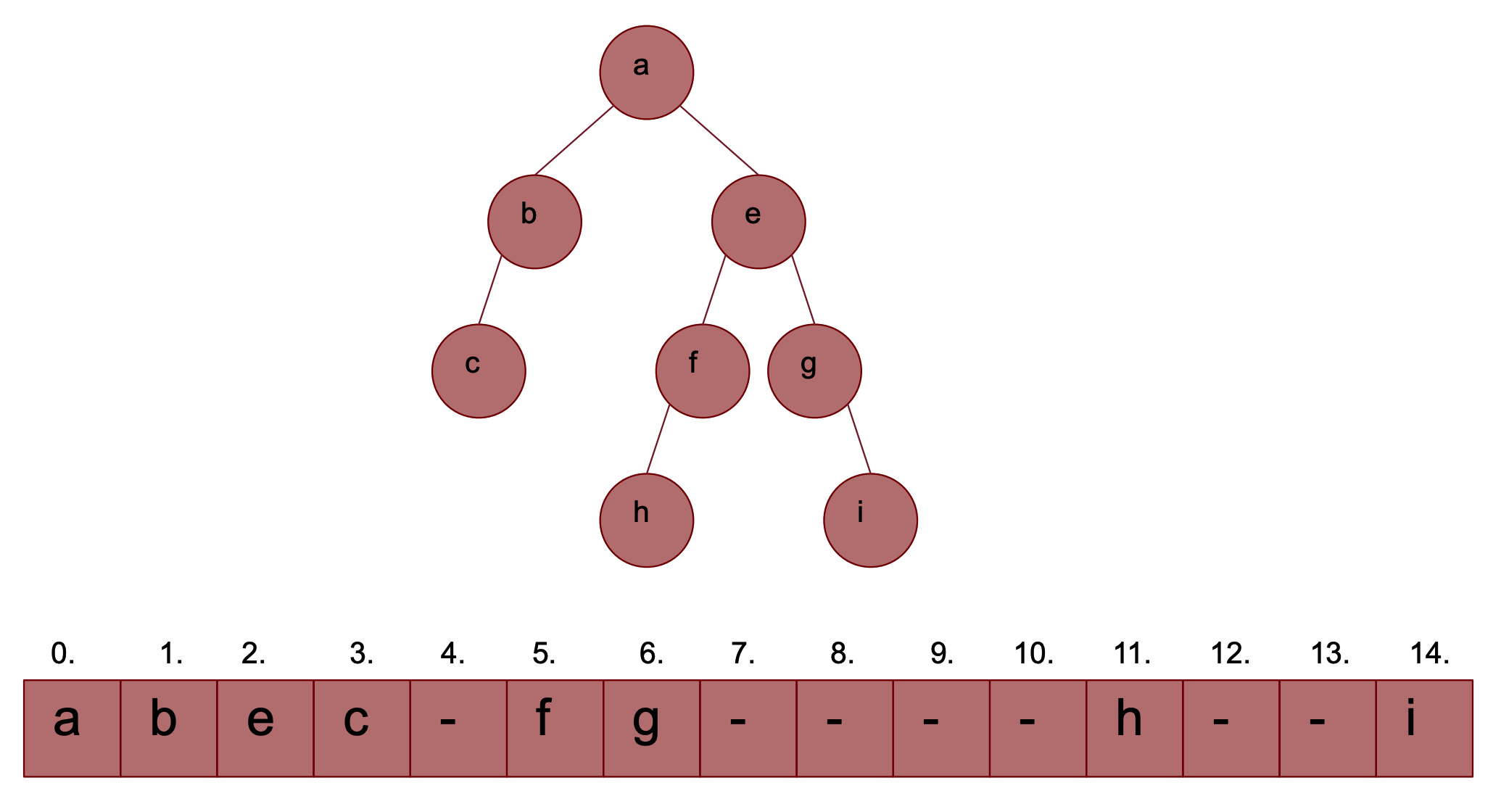
Vettore dei Padri

È costituito da un vettore P dove l’elemento $P [i]$ contiene l’indice del padre del nodo $i$ nell’albero. Questo metodo funziona anche con alberi non necessariamente binari.

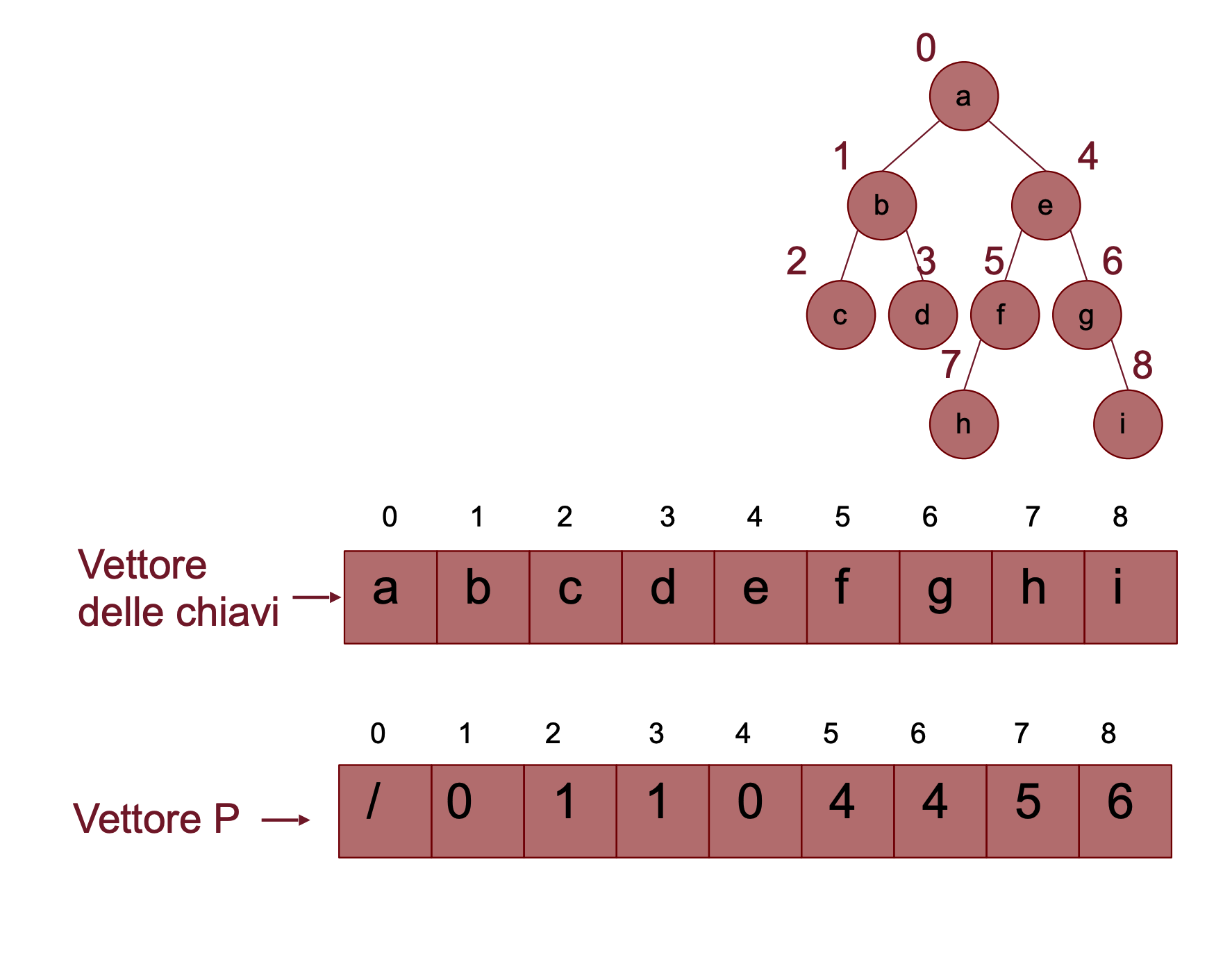
Trovare il padre di un nodo

Struttura a puntatori: Non possiamo farlo dato che accediamo all’albero dalla radice e poi non possiamo scorrere l’albero come una lista dato che non sappiamo se andare a destra o sinistra.
Rappresentazione Posizionale: Si utilizza la formula $⌊ \frac{i - 1}{2} ⌋$ per il padre del nodo $i$
Vettore dei Padri: L’indice del padre si trova nel vettore $P$ nell’elemento $P [i]$

Determinare se il nodo ha 0, 1 o 2 figli

Struttura a puntatori: Dobbiamo controllare i campi left e right del nodo
Rappresentazione Posizionale: Controlliamo gli elementi di indice $2 i + 1$ e $2 i + 2$
Vettore dei Padri: Scorriamo il vettore P e contiamo le occorrenze dell’elemento $i$ che è l’indice del nodo che vogliamo controllare

Determinare la distanza di un nodo dalla radice

Struttura a Puntatori: Non possiamo, dobbiamo capire come navigare l’albero prima, quindi se andare a destra o sinistra.
Rappresentazione Posizionale: Usiamo la formula $⌊ lo g_{2} i ⌋$ che è il livello del nodo $i$ equivalente quindi alla sua distanza.
Vettore dei Padri: A partire ad $i$ risaliamo di padre in padre passando quindi per $P [i], P [P [i]], P [P [P [i]]]$ fino ad arrivare alla radice

Visite ad Alberi

Una delle operazioni più basilari che possiamo effettuare su un albero è la visita di tutti i suoi nodi per effettuare operazioni su di essi, notiamo che un albero possiamo visitarlo in più modi in base all’ordine in cui entriamo in ogni nodo:

Visita in preordine (preorder): Il nodo è visitato prima di proseguire la visita nei suoi sottoalberi
Visita inordine (inorder): Il nodo è visitato dopo la visita del sottoalbero sinistro e prima di quella del sottoalbero destro
Visita postordine (postorder): Il nodo è visitato dopo entrambe le visite dei sottoalberi

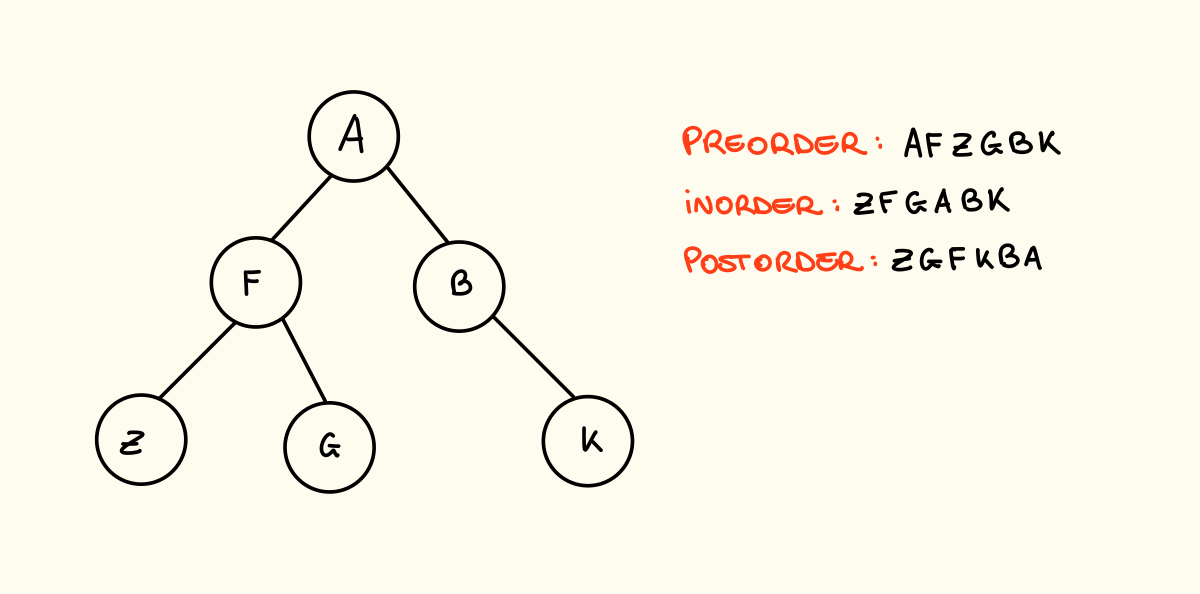
Sotto il punto di vista del codice, possiamo considerare un albero memorizzato con record e puntatori ed effettuare i 3 tipi di visite in questo modo:

def VisitaPreordine(p):
	if p != None:
		# Operazioni sul nodo
		VisitaPreordine(p.left)
		VisitaPreordine(p.right)
 
def InOrdine(p):
	if p != None:
		VisitaInOrdine(p.left)
		#Operazioni sul nodo
		VisitaPreordine(p.right)
 
def VisitaPostOrdine(p):
	if p != None:
		VisitaPostOrdine(p.left)
		VisitaPostOrdine(p.right)
		# Operazioni sul nodo

Il costo computazionale ovviamente è uguale per tutti i tipi di visita e varia solamente in base alla struttura utilizzata per memorizzare l’albero.

Detto $k$ il numero di nodi del sottoalbero sinistro della radice con $0 \leq k \leq n - 1$ , abbiamo la seguente equazione di ricorrenza:

T (n) = T (k) + T (n - 1 - k) + θ (1) T (0) = θ (1)

Quindi $T (k)$ indica le visite al sottoalbero sinistro esclusa la radice, $T (n - 1 - k)$ indica la visite al sottoalbero destro esclusa la radice e $θ (1)$ è la visita alla radice.

Abbiamo diverse soluzioni in base alla composizione dell’albero

Albero Completo

In questo caso abbiamo che $k = \frac{n}{2}$ e quindi l’equazione diventa

T (n) = 2 T (\frac{n}{2}) + θ (1)

Questa è facilmente risolvibile con il Master Theorem perché ricadiamo nel secondo caso e abbiamo un costo computazionale di $θ (n)$

Albero Massimamente Sbilanciato

Questo si verifica quando il sotto albero sinistro è completamente vuoto quindi $k = 0$ oppure quando è vuoto quello destro e quindi $n - 1 - k = 0$ in questi casi otteniamo:

T (n) = T (n - 1) + θ (1)

Che è risolvibile con il metodo iterativo ottenendo il costo computazionale di $θ (n)$

Costo Generale

Questi due esempi ci fanno capire che la composizione dell’albero in realtà non conta nulla nel costo della visita, questa sarà sempre $θ (n)$ , Dimostrabile con Sostituzione.

Ognuna delle 3 visite ci può tornare utile in determinati contesti, un esempio molto semplice è quando dobbiamo stabilire se una determinata chiave è presente nell’albero o no, in questo caso è utile una visita in preordine che ci permette di controllare il nodo prima ancora di andare a controllare inutilmente eventuali sottoalberi.

Visita per Livelli

Nessuna delle visite che abbiamo visto ci permette di accedere ai nodi livello per livello, per fare questo tipo di visita infatti abbiamo bisogno di una coda d’appoggio nella quale inseriamo i nodi per poi estrarli durante la visita.

Pseudocodice per la stampa dei valori con visita per livelli

def VisitaPerLivelli(r):
	if r == None:
		return
	testa, coda = inserisciCoda(None, None, r)
	while testa != None:
		p, testa, coda = estraiCoda(testa, coda)
		print(p.key)
		if p.left:
			testa, coda = inserisciCoda(testa, coda, p.left)
		if p.right:
			testa, coda = inserisciCoda(testa, coda, p.right)

Le funzioni di inserimento e estrazione dalla coda prendono in input i puntatori a testa, coda e nel caso dell’inserimento anche il valore da aggiungere. L’inserimento restituisce i nuovi puntatori testa e coda mentre l’estrazione restituisce anche il valore estratto. Codice

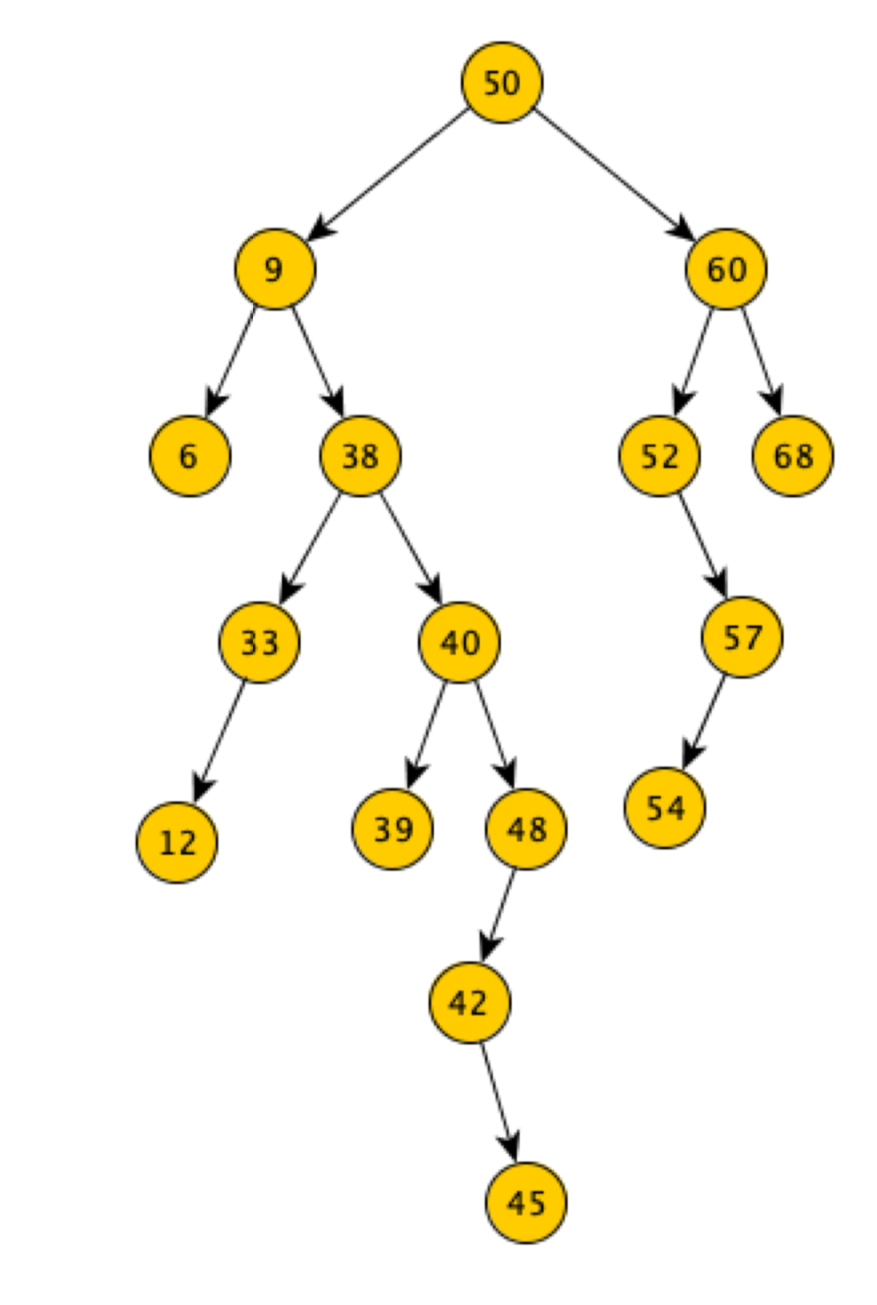
Alberi Binari di Ricerca

Un albero binario di ricerca è un albero dove vengono mantenute le seguenti proprietà:

Ogni nodo contiene una chiave
Il valore della chiave contenuta in ogni nodo è maggiore della chiave contenuta in ciascun nodo del suo sottoalbero sinistro
Il valore della chiave contenuta in ogni nodo è minore della chiave contenuta in ciascun nodo del suo sottoalbero destro

Esempio

Questo tipo di alberi permette le operazioni che abbiamo già visto quindi:

Search(T, k): Restituisce un puntatore all’elemento con chiave di valore $k$ in $T$ se presente
Minimum(T) / Maximum(T): Restituisce un puntatore all’elemento di valore minimo / massimo nell’albero $T$
Insert(T, x): Inserisce un elemento di valore $x$ in $T$
Delete(T,x): Elimina da $T$ il nodo con l’elemento $x$ se presente

Un albero di questo tipo può essere utilizzato come coda di priorità, infatti il minimo è sempre nel nodo più a sinistra mentre il massimo in quello più a destra. È importante ricordare che l’elemento più a sinitra o più a destra non è necessariamente una foglia, può anche essere il nodo più a sinistra che non ha figli sinistri o il nodo più a destra che non ha figli destri.

Stampare tutte le chiavi in ordine crescente Per fare questo ci basta visitare l’albero con una visita inorder

Con questo tipo di alberi possiamo anche costruire degli algoritmi di ordinamento:

Inseriamo le $n$ chiavi da ordinare nell’albero
Visitiamo inorder l’albero appena costruito

Il costo computazionale è $T (cos t r u z i o n e) + T (v i s i t a) = T (C os t r u z i o n e) + θ (n)$ , il costo della costruzione lo determineremo più avanti

D’ora in avanti assumiamo che l’ABR sia memorizzato tramite record e puntatori e che abbia in più anche un puntatore al padre.

Implementiamo quindi una funzione generaABR(A) che dato un array di interi A generi un albero di ricerca

def generaABR(A):
	lista = sorted(A, reverse=True)
	return generaABR1(len(A), lista)
 
def generaABR1(n, lista):
	if n == 0:
		return None
	p = NodoABR()
	s = random.randint(0, n-1) # Numero di figli del sottoalbero sx
	p.left = generaABR1(s, lista) # Genera sottoalbero sx
	p.key = lista.pop() # Assegna chiave al nodo
	p.right = generaABR1(n-1-s, lista) # Genera sottoalbero dx
	if p.left:
		p.left.parent = p
	if p.right:
		p.right.parent = p
	return p

Con gli ultimi if facciamo in modo di linkare anche le foglie ai nodi precedenti.

Ricerca

È molto simile alla ricerca binaria, la funzione riceve il puntatore alla radice e la chiave da ricercare ed esegue una discesa guidata.

def ricercaABR(p, x):
	if p == None or p.key == x:
		return p
	if x < p.key:
		return ricercaABR(p.left, x)
	else:
		return ricercaABR(p.right, x)

Complessità di $θ (h)$ dove $h$ è l’altezza dell’albero

In questo tipo di alberi non possiamo garantire un costo logaritmico come gli alberi binari completi dato che non possiamo garantire il bilanciamento dell’albero

Inserimento

Eseguiamo una discesa guidata come nella ricerca, quando arriviamo a punto in cui decidiamo di scendere in un puntatore vuoto allora in quella posizione aggiungiamo il nodo contente il nuovo valore. Notare che il padre di tale nuovo nodo potrebbe essere una foglia o più in generale è un nodo a cui manca il figlio corrispondente alla direzione che si dovrebbe prendere per proseguire, gli elementi vanno quindi agganciati tra padre e figlio

def InserisciABR(p, x):
	z = NodoABR(x)
	if p == None:
		return z
	q = p
	while True:
	# Scendo fino alla prima posizione None
		if q.key > x and q.left != None:
			q = q.left
		elif q.key < x and q.right != None:
			q = q.right
		else:
			break
	if q.key == x:
	# Elemento già presente
		return p
	# Collego il nodo z al nodo q
	z.parent = q # Imposto il padre di z
	# Imposto se z è figlio sinistro o destro di q
	if q.key > x:
		q.left = z
	else:
		q.right = z
	return p

Il ciclo viene eseguito al massimo $h$ volte quindi $T (n) = O (h)$

Minimo e Massimo

Il minimo si trova al nodo più a sinistra mentre il massimo nel nodo più a destra, quindi scendiamo dalla radice fino a quando non troviamo un nodo che non ha figlio sinistro / destro. $T (n) = O (h)$

Cancellazione

Per eliminare un nodo distinguiamo 3 casi in funzione del numero di figli che ha il nodo da cancellare.

Caso 1: Se il nodo è una foglia la si elimina ponendo a None il nodo .left o .right del padre
Caso 2: Se il nodo ha un solo figlio lo si “cortocircuita”, si collegano fra loro suo padre e il suo unico figlio indipendentemente chi sia destro o sinistro.
Caso 3: Se il nodo ha 2 figli si sostituisce il suo valore sostituendolo con quello del figlio sinistro e si scende a cancellare il figlio di sinistra, dopo un certo numero di passi arriveremo al caso 1 o 2.

def cancellaABR(p, x):
	# Casi in cui p va eliminato
	# In questo caso significa che l'albero ha un solo nodo e corrisponde al valore che vogliamo cancellare
	if p == None or (p.key == x and p.left == p.right == None):
		return None
 
	# Se p vale x e non abbiamo figlio sinistro bypassiamo con il destro
	if p.key == x and p.left == None:
		p = p.right
		p.parent = None
		return p
 
# Se p vale x e non abbiamo figlio destro bypassiamo con il sinistro
	if p.key == x and p.right == None:
		p = p.left 
		p.parent = None
		return p
 
# Finiti Casi base
 
# Salviamo il puntatore iniziale e scendiamo nell'albero fino ad incontrare q.key == x
	q = p 
	while q != None and q.key != x:
		if x < q.key:
			q = q.left
		else:
			q = q.right
 
# Usciti dal ciclo
# Se q punta a None non abbiamo trovato x quindi terminiamo il programma
	if q == None:
		return p
 
# Altrimenti q si trova sul nodo con valore x
# Finchè q ha due figli facciamo risalire il contenuto del figlio di sinistra e scendiamo con il puntatore fino ad arrivare ad un nodo con al più un figlio che verrà cancellato (da Caso 3 passiamo a caso 2 o 1)
	while q.left != None and q.right != None:
		q.key = q.left.key
		q = q.left
		
	s = None
	# Dobbiamo modificare il padre di q (nodo da cancellare), se q non ha figli il padre non deve puntare a nulla (s rimane None) altrimenti il padre deve puntare a S che a sua volta punterà ai figli di q.
# In questi due if facciamo puntare S al figlio destro o sinistro di q o a None se non esistono e aggiorniamo anche S facendogli avere come padre q.parent
	if q.left != None:
		s = q.left
		s.parent = q.parent
	if q.right != None:
		s = q.right
		s.parent = q.parent
	# Con questi ultimi if modifichiamo il padre di q e lo facciamo puntare a S
	if q.parent.left == q:
		q.parent.left = s
	else:
		q.parent.right = s
	return p

Dizionari

I dizionari ci permettono di gestire un insieme dinamico di dati, non ha quindi una dimensione fissa, possiamo realizzare su di essi le 3 operazioni di:

insert
search
delete

Fra le strutture dati che conosciamo quelle che supportano queste tre operazioni sono vettori, liste concatenate e alberi. Ogni struttura ha tempi diversi per eseguire queste operazioni ma quando si deve realizzare un dizionari si ricorre a una tabella hash, queste infatti implementano le 3 operazioni con complessità media costante $θ (1)$ . Vediamo 2 diversi tipi di tabelle: a hash chiuso e ad hash aperto.

Dobbiamo gestire un insieme dinamico i cui elementi hanno chiavi distinte intere $\in U = {0, 1, \dots, m - 1}$ detto insieme universo. La prima idea è quella di creare un vettore in modo tale da avere ogni chiave ad un indice ed eseguire quindi le 3 operazioni in tempo costante ad accesso diretto all’indice. Potrebbero però verificarsi diversi problemi:

L’insieme $U$ potrebbe essere molto grande da non permettere l’allocazione in memoria di un vettore abbastanza capiente da contenerlo.
Le chiavi realmente utilizzate potrebbero essere molte poche e quindi sprecheremo molto spazio con posizioni dell’array lasciate vuote.

Esempio:

Il codice fiscale è composto da 8 lettere e 7 cifre, consideriamo un alfabeto di 26 lettere e le combinazioni possibili di codici sono:

U = 2 6^{8} \cdot 1 0^{7}

Il numero di cittadini però è inferiore a $6 \cdot 1 0^{7}$ , è quindi presente una grande differenza tra le chiavi possibili e le chiavi realmente utilizzate.

Indirizzamento Diretto

L’indirizzamento diretto con un array è quindi efficiente quando l’universo delle chiavi è piccolo e molto vicino al numero degli elementi.

Possiamo misurare il grado di riempimento di una tabella con il fattore di carico:

a = \frac{n}{m}

Dove $m$ è la dimensione della tabella e $n$ sono le chiavi effettivamente utilizzate, esempio dobbiamo memorizzare 100 studenti tramite la loro matricola (6 cifre):

a = \frac{100}{1 0 ^{6}} = 0.0001

Più il numero è piccolo più spazio stiamo sprecando.

Con le tabelle hash abbiamo un buon compromesso tra memoria utilizzata e tempi computazionali:

Memoria richiesta: $θ (n)$
Tempo di ricerca: $θ (1)$ nel caso medio ma non nel caso pessimo

Tabelle Hash

Dobbiamo innanzitutto dimensionare la tabella in base al numero di elementi attesi che indicheremo con $m$ e poi utilizzare una funzione detta di hash per indicizzarli. Una funzione hash è una funzione che data una chiave $x$ restituisce la posizione nella tabella in cui l’elemento con chiave $x$ viene memorizzato. La dimensione della tabella spesso non coincide con la dimensione dell’universo e molto spesso è anche più piccola di quest’ultimo.

Quindi data la chiave di un elemento tramite la funzione di hash otteniamo la sua posizione nella tabella, in questo modo:

Riduciamo lo spazio necessario per memorizzare la tabella Ma allo stesso tempo:
Perdiamo la corrispondenza tra chiavi e posizioni in tabella
Possono verificarsi delle collisioni.

Una collisione accade quando due elementi con chiave diversa restituiscono lo stesso valore dalla funzione di hash. Il verificarsi di collisioni è inevitabile quando l’insieme dei valori possibili delle chiavi degli elementi che dobbiamo inserire è molto grande e invece il numero degli indici disponibili nella mappa è molto piccolo rispetto ad esso. Comunque una collisione può verificarsi anche nel caso opposto quindi dove le chiavi possibili sono minori del numero degli elementi nella mappa.

Le collisioni vanno quindi evitate il più possibile e se capitano vanno risolte.

L’obiettivo della funzione hash quindi, oltre a restituirci l’indice in tabella data una chiave, è anche quello di distribuire uniformemente i dati in modo casuale all’interno di un range ed evitare le collisioni il più possibile.

Esempio:

Abbiamo una tabella di dimensione $m$ dove vogliamo inserire delle stringhe, una possibile funzione hash per le stringhe è la seguente:

def hash(s, size):
	h = 0
	for c in s:
		h += ord(c)
	return h % size

Quindi sommiamo il valore ASCII di tutti i caratteri e poi prendiamo il resto dalla divisione con la grandezza della tabella per assicurarci di rimanere all’interno del range.

Collisioni: È possibile che due stringhe diverse producano lo stesso valore ASCII e quindi lo stesso hashcode. Distribuzione: Il valore ASCII non è buon metodo per distribuire uniformemente i dati dato che combinazioni di caratteri potrebbero avere valori molto simili oppure molto diversi. Efficienza: Calcolare la somma dei valori ASCII di tutti i caratteri per stringhe molto lunghe può costare molto tempo, una funzione di hash deve calcolare il valore in modo rapido indipendentemente dalla lunghezza della stringa.

Uniformità semplice della funzione hash

La situazione ideale è quella dove ciascuna posizione della tabella è scelta con la stessa probabilità. In ogni caso però, anche con un’ottima funzione di hash, le collisioni possono verificarsi.

Per risolvere le collisioni esistono due metodi: Indirizzamento Chiuso (liste di trabocco) e Indirizzamento Aperto.

Liste di Trabocco

Questo metodo prevede di far corrispondere ad ogni indice della tabella invece dell’elemento una Lista linkata detta lista di trabocco, in questo modo ogni elemento che deve essere inserito in quell’indice viene inserito nella lista.

Inserimento: Se inseriamo gli elementi in cima alla lista abbiamo un costo di inserimento pari a $θ (1)$ . Ricerca: Dopo aver eseguito l’accesso all’indice della mappa dobbiamo cercare l’elemento all’interno della lista quindi abbiamo un costo $O (l u n g h ezz a l i s t a)$ . Nel caso peggiore ovvero quando tutti gli elementi della mappa sono nella stessa lista $O (n)$ ma nel caso medio ovvero quando gli elementi sono distribuiti equamente $O (1 + \frac{n}{m})$ .

Queste liste bilanciano sia lo spazio che il tempo necessario, infatti:

Se $m = 1$ quindi la tabella ha una sola posizione e quindi una sola lista, la tabella è a tutti gli effetti una lista linkata e quindi abbiamo tempo e spazio $O (n)$ .
Se $m = U$ e abbiamo un hash perfetto, su ogni riga abbiamo un solo elemento quindi abbiamo un tempo di $O (1)$ ma spazio $O (U)$ .
Se $1 \leq m \leq U$ e la funzione di hash gode dell’uniformità semplice distribuendo quindi gli elementi in modo equo allora abbiamo un costo di tempo $O (1 + \frac{n}{m})$ e spazio $O (m + n)$ .

Indirizzamento Aperto

Con questo metodo inseriamo direttamente tutti gli elementi nella tabella senza usare altre strutture dati di supporto, questa tecnica è applicabile però soltanto nel caso in cui abbiamo la dimensione della mappa più grande delle possibili chiavi da inserire, quindi $n \leq m$ e abbiamo anche un fattore di carico $\leq 1$ .

Ad esempio, vogliamo inserire una chiave $k$ ma la sua posizione data dalla funzione hash è già occupata, con l’indirizzamento aperto andiamo ad occupare un’altra posizione anche se quest’ultima spetta ad un’altra chiave.

In questo modo utilizziamo meno memoria dato che non abbiamo bisogno di puntatori a liste.

Per realizzare questo metodo dobbiamo modificare la nostra funzione di hash, questa infatti deve dipendere sia dalla chiave ma anche dal numero di collisioni già trovate. Quindi se una volta calcolato un hash finiamo in una posizione occupata riutilizziamo l’hash con il numero di collisioni incrementato e cerchiamo un’altra posizione.

Otteniamo una sequenza di ricerca del tipo:

H (k, 0); H (k, 1); \dots; H (k, m - 1)

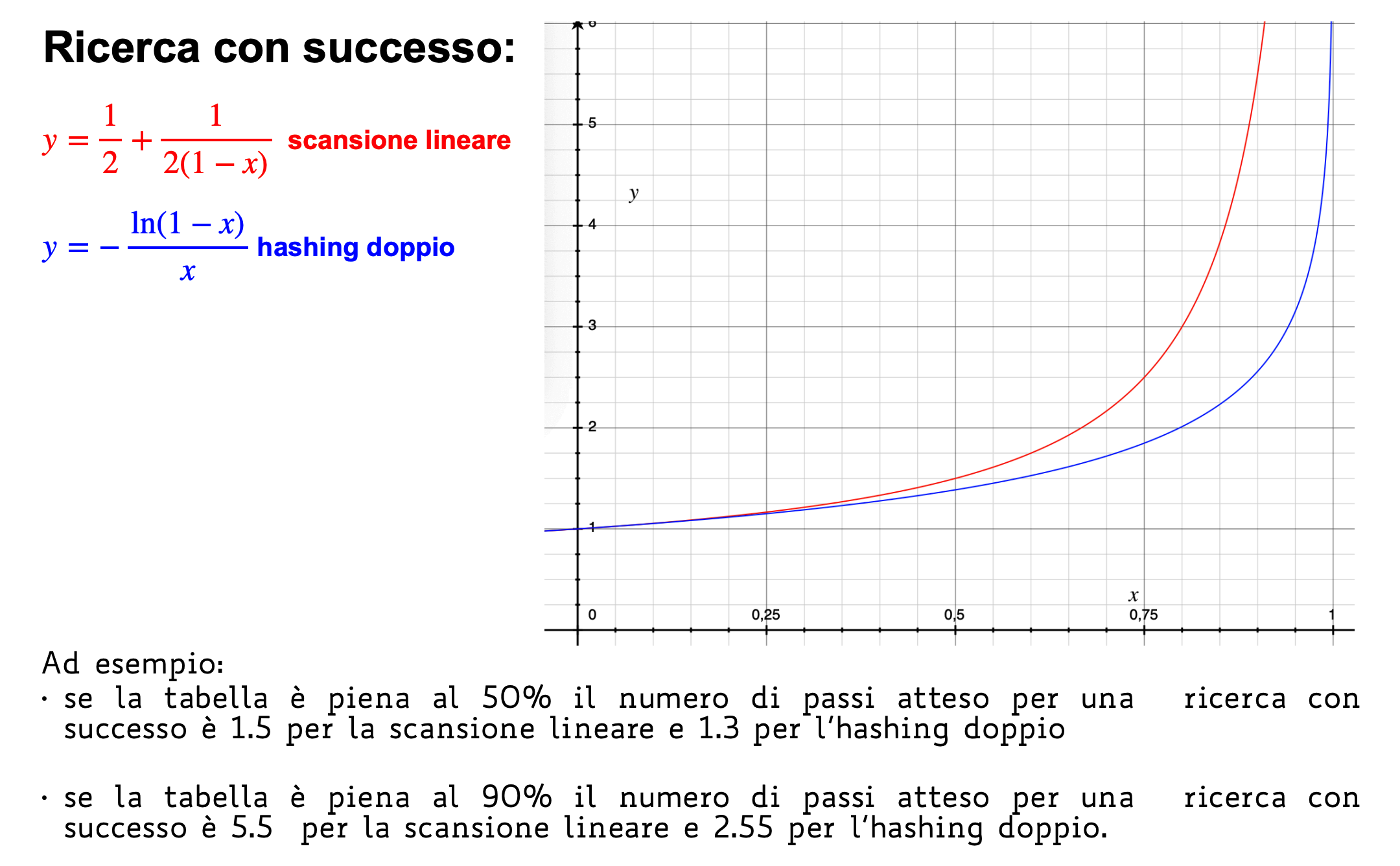
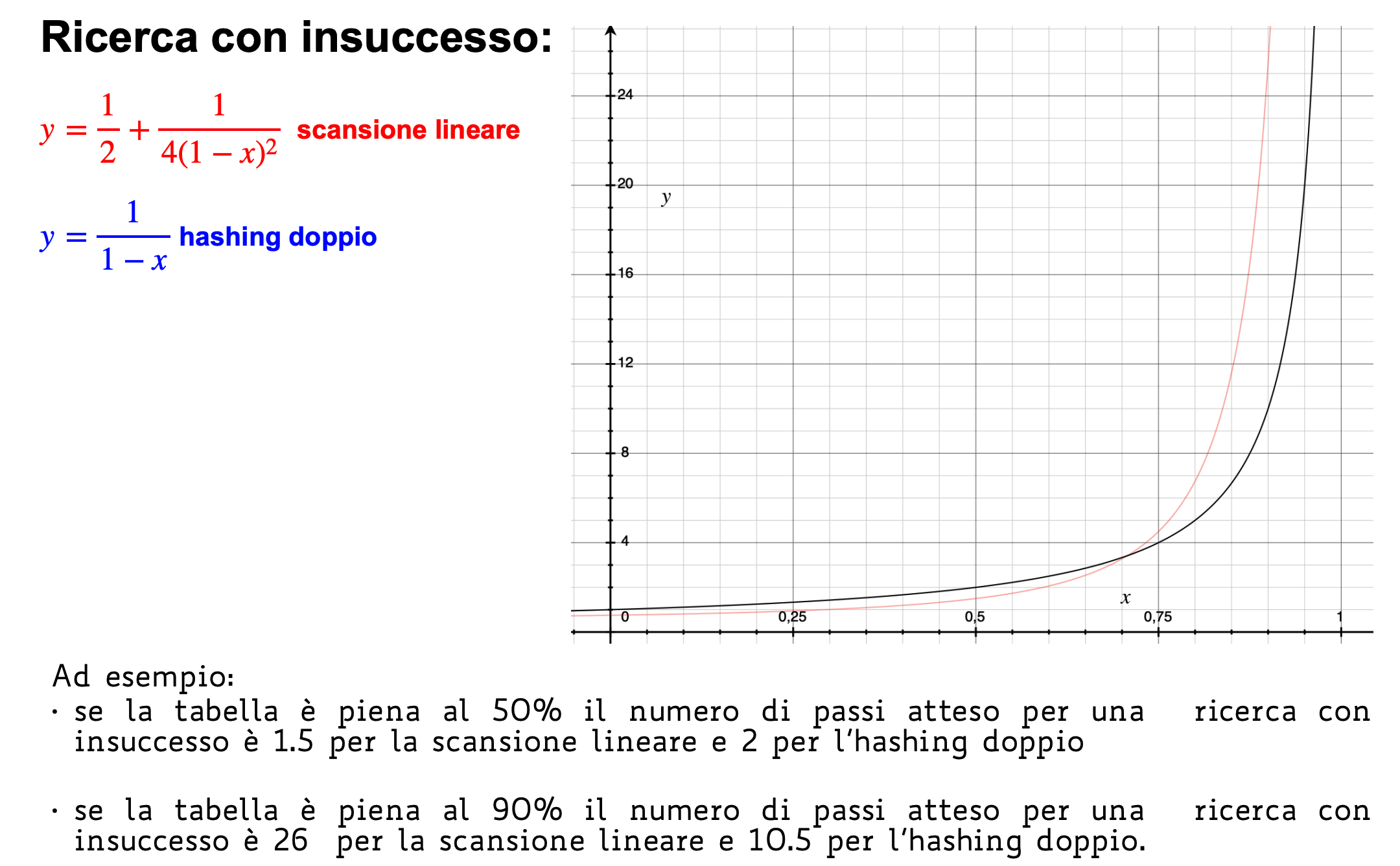
Inserimento: Per effettuare questa scansione esistono diverse tecniche:

Nota: i è il numero di collisioni e quindi va da 0 a m-1.

Ispezione Lineare: Quando si incontra una collisione si utilizza l’indice successivo a quello che collide fino a trovare una posizione libera $H (k, i) = (h (k) + i) % m$
Doppio Hashing: Si utilizzano due funzioni hash $H (k, i) = (h_{1} (k) + i \cdot h_{2} (k)) % m$

Per assicurarci che la sequenza contenga tutti gli indici è necessario che $m$ e $h_{2} (k)$ siano primi tra loro, possiamo ad esempio scegliere:
- $m$ primo
- $h_{1} (k) = k % m$
- $h_{2} (k) = (k % (m - 1)) + 1$

Ricerca: Per la ricerca non cambia nulla, infatti ci basta scandire la tabella allo stesso modo dell’inserimento e se troviamo una chiave la restituiamo altrimenti se finiamo in una cella vuota la chiave non è presente.

Cancellazione: Per la cancellazione la prima idea è quella di impostare a None l’elemento ma questo comporterebbe problemi per la ricerca, infatti durante la scansione potremmo finire in una cella None e interrompere la ricerca prima del dovuto. Possiamo invece marcare le celle cancellate con un valore canc, l’inserimento le considererà come celle vuote mentre la ricerca come celle che hanno un valore e quindi proseguirà a cercare la chiave.

Tempi:

👨🏻‍💻 Alem's Notes

Strutture Dati

Operazioni di Interrogazione

Operazioni di Manipolazione

Vettore

Liste Semplici con Puntatori

Creazione di una Lista Puntata

Stampa di una Lista Puntata

Ricerca nelle Liste Puntate

Inserimento nelle Liste Puntate

Inserimento dopo alcuni valori

Eliminazione nelle Liste Puntate

Liste Doppiamente Puntate

Creazione

Pila

Implementazione con Liste Puntate - Push

Implementazione con Liste Puntate - Estrazione

Coda

Implementazione con Liste Puntate - Enqueue

Implementazione con Liste Puntate - Dequeue

Code con priorità

Alberi

Alberi Radicati

Alberi Binari

Rappresentazione di un Albero Binario in Memoria

Memorizzazione tramite Record e Puntatori

Rappresentazione Posizionale

Vettore dei Padri

Trovare il padre di un nodo

Determinare se il nodo ha 0, 1 o 2 figli

Determinare la distanza di un nodo dalla radice

Visite ad Alberi

Albero Completo

Albero Massimamente Sbilanciato

Costo Generale

Visita per Livelli

Alberi Binari di Ricerca

Ricerca

Inserimento

Minimo e Massimo

Cancellazione

Dizionari

Tabelle Hash

Liste di Trabocco

Indirizzamento Aperto

Table of Contents

Backlinks