Serie Numeriche

Introduciamo il concetto di serie considerando una successione di numeri Reali.

$$a_1,a_2,a_3,...,a_n$$

Calcolare la somma di tutti questi numeri equivale a calcolare la serie

$$a_1+a_2+...+a_n=\sum _{n=1}^{+\infty }{a}_n$$

Dove $a_n$ è detto termine generale della serie. Questa scrittura nei termini generali delle somme non ha molto senso perché non stiamo sommando un numero finito di numeri, ma consideriamo invece questa scrittura:

$$\begin{array}{rl}& s_1=a_1\\ & s_2=a_1+a_2\\ & s_3=a_1+a_2+a_3\\ & s_n=a_1+a_2+a_3+...+a_n\end{array}$$

Quindi se noi volessimo sapere la somma di tutti gli $n$ termini ci basta calcolare:

$$s=\underset{n\to +\infty }{\lim }{s}_n$$

E a seconda del risultato si possono verificare 3 casi:

• $l\in \mathbb{R}$: Si dice che la serie converge
• $\pm \infty$: Si dice che la serie diverge
• Se il limite non esiste la serie si dice indeterminata

Un esempio di serie indeterminata è la seguente:

$$\sum _{n=0}^{+\infty }(-1{)}^n=+1-1+1-1+1+...$$

Infatti la serie non si stabilizzerà mai.

Serie Geometriche

Consideriamo di avere un numero $q\in \mathbb{R}$, si definisce serie geometrica la seguente serie:

$$\sum _{n=0}^{+\infty }{q}^n$$

Quindi una serie si dice geometrica quando alla base abbiamo una quantità indipendente da n

Perché si dice geometrica?

Perché tutti i termini della serie costituiscono una progressione geometrica ovvero quando il rapporto tra un termine e il suo precedente è costante. Esempio con q = 2: $1+2+4+8+16+32$ Il rapporto è sempre uguale a 2 tranne per il primo termine che ovviamente non può essere confrontato con altro

Secondo la teoria delle progressioni se $q\ne 1$ la somma dei primi n numeri equivale a:

$$S_n=\frac{1-q^n}{1-q}\underset{n\to +\infty }{\lim }{S}_n=S$$

Grazie a questa formula possiamo studiare dei casi:

• $|q|<1$: In questo caso il termine $q^n$ tenderà a 0 e quindi la serie converge al valore $\frac{1}{1-q}$
• $q=1$: È banale notare che stiamo sommando infinite volte 1 quindi la serie diverge
• $q>1$: Anche in questo caso notiamo che andremo a sommare numeri sempre più grandi quindi la serie diverge
• $q<-1$: La serie oscilla verso numeri sempre più grandi ma sia positivi che negativi, ad esempio se prendiamo $q=-2$ otteniamo: $1-2+4-8+16-32+64-...$

Attenzione agli indici

La formula per calcolare il valore della somma vale quando contiamo tutti i termini quindi partendo da $n=0$, nel caso in cui partissimo da un indice diverso dobbiamo togliere i primi termini aggiuntivi. Esempio: $\sum _{n=2}^{+\infty }(\frac{1}{2}{)}^{n+2}=\frac{1}{4}\sum _{n=2}^{+\infty }(\frac{1}{2}{)}^n=\frac{1}{4}[\frac{1}{1-1/2}-1-1/2]=\frac{1}{8}$

Criterio del rapporto

Consideriamo di avere una serie a infiniti termini positivi, se:

$$\exists h\in \mathbb{R}0<h<1\text{ tale che }\frac{a_{n+1}}{a_n}\le h$$

Qualsiasi sia $n$ o anche da un certo $n$ in poi, se esiste possiamo dire che la serie converge, se invece il rapporto è maggiore o uguale a 1 la serie diverge

Per svolgere gli esercizi però è utile considerare casi diversi:

$$\begin{array}{rl}& \underset{n\to +\infty }{\lim }\frac{a_{n+1}}{a_n}=l\\ & \\ & l<1\text{: La serie converge}\\ & l>1\text{: La serie diverge}\\ & l=1\text{: Dobbiamo utilizzare un altro metodo}\end{array}$$

Esempi:

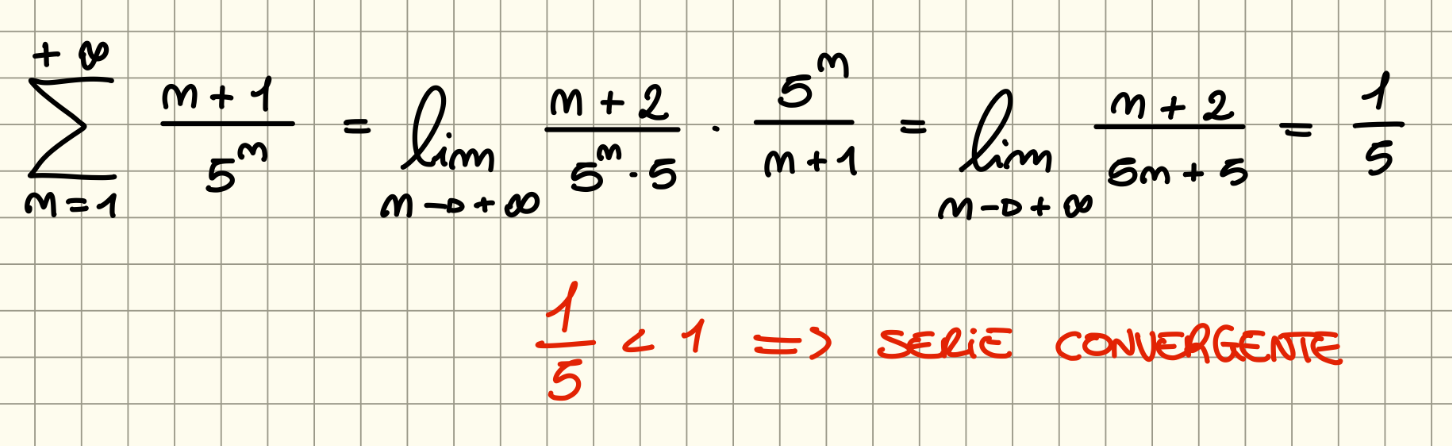
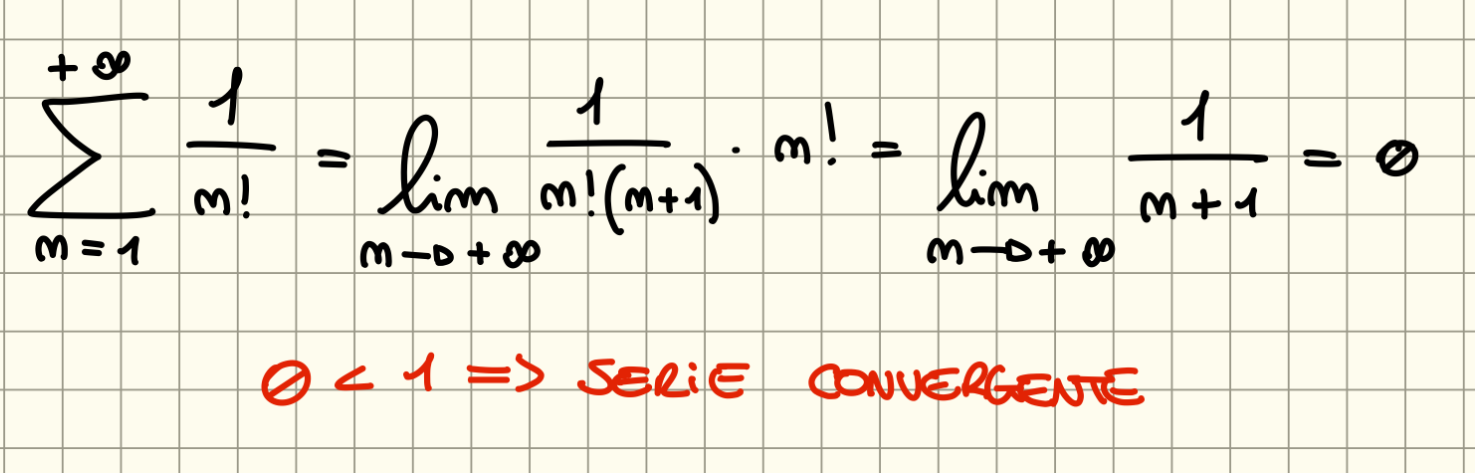
Criterio della Radice

Consideriamo sempre una serie a infiniti termini positivi, il criterio della radice è molto simile a quello del rapporto visto precedentemente, infatti abbiamo li stessi 3 casi ma con un procedimento diverso:

$$\begin{array}{rl}& {\sqrt[n]{a}}_n=l\\ & \\ & l<1\text{: La serie converge}\\ & l>1\text{: La serie diverge}\\ & l=1\text{: Dobbiamo utilizzare un altro metodo}\end{array}$$

Esempi:

Serie Armonica

La serie armonica è una serie dove il termine generale è $\frac{1}{n}$ quindi la serie è uguale a:

$$\sum _{n=1}^{+\infty }\frac{1}{n}$$

Utilizzando metodi di confronto non riusciremo a dimostrare che questa serie diverge, come facciamo quindi? La serie armonica equivale quindi a:

$$\begin{array}{r}1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+...\end{array}$$

Per dimostrare che converge possiamo fare dei piccoli raggruppamenti e notiamo che andremo a sommare sempre $\frac{1}{2}$ :

$$\begin{array}{r}1+\frac{1}{2}+(\frac{1}{3}+\frac{1}{4})+(\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8})+(\frac{1}{9}+...+\frac{1}{16})\end{array}$$

Teorema generale di Convergenza

Se una serie converge allora la successione è infinitesima, ma se una successione è infinitesima non è detto che la serie converga. Esempio la serie armonica

Serie Armonica Generalizzata

Il termine generale delle serie armoniche è $\frac{1}{n^k}$ con $k\in \mathbb{R}$ quindi la serie è:

$$\sum _{n=1}^{+\infty }\frac{1}{n^k}$$

Se:

• $k>1$: La serie converge
• $k\le 1$: La serie diverge

Criterio del Confronto

Consideriamo di avere due serie a termini positivi

$$\begin{array}{rl}& \sum _{n=1}^{+\infty }{a}_n=a_1+a_2+...+a_n\\ & \sum _{n=1}^{+\infty }{b}_n=b_1+b_2+...+b_n\end{array}$$

Adesso supponiamo che ogni termine della prima serie sia $a_n\le b_n$, in questo caso si dice che la serie $a_n$ è la minorante di $b_n$ oppure che quest’ultima è la maggiorante di $a_n$

Adesso si possono verificare più casi:

• Se $\sum _{n=1}^{+\infty }{b}_n$ converge allora anche $\sum _{n=1}^{+\infty }{a}_n$ converge
• Se $\sum _{n=1}^{+\infty }{a}_n$ diverge allora anche $\sum _{n=1}^{+\infty }{b}_n$ diverge

Tutti gli altri casi non ci danno informazioni utili

Esempio

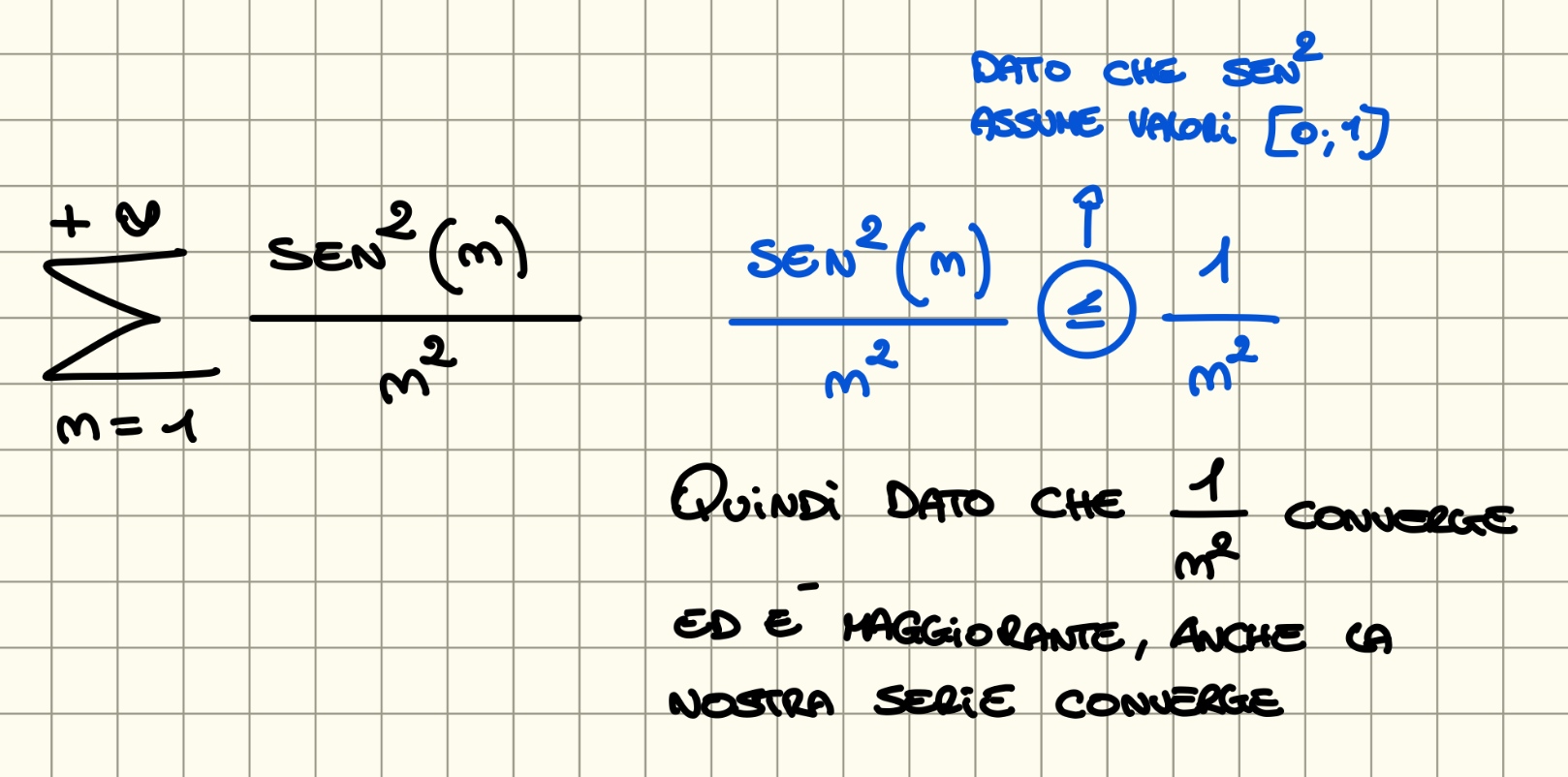
Criterio del Confronto Asintotico

Consideriamo di avere due serie a termini positivi

$$\begin{array}{rl}& \sum _{n=1}^{+\infty }{a}_n;\sum _{n=1}^{+\infty }{b}_n\\ & \text{Consideriamo adesso il limite}\\ & \underset{n\to +\infty }{\lim }\frac{a_n}{b_n}=l\ne 0\\ & \text{Allora le due serie si comportano allo stesso modo}\end{array}$$

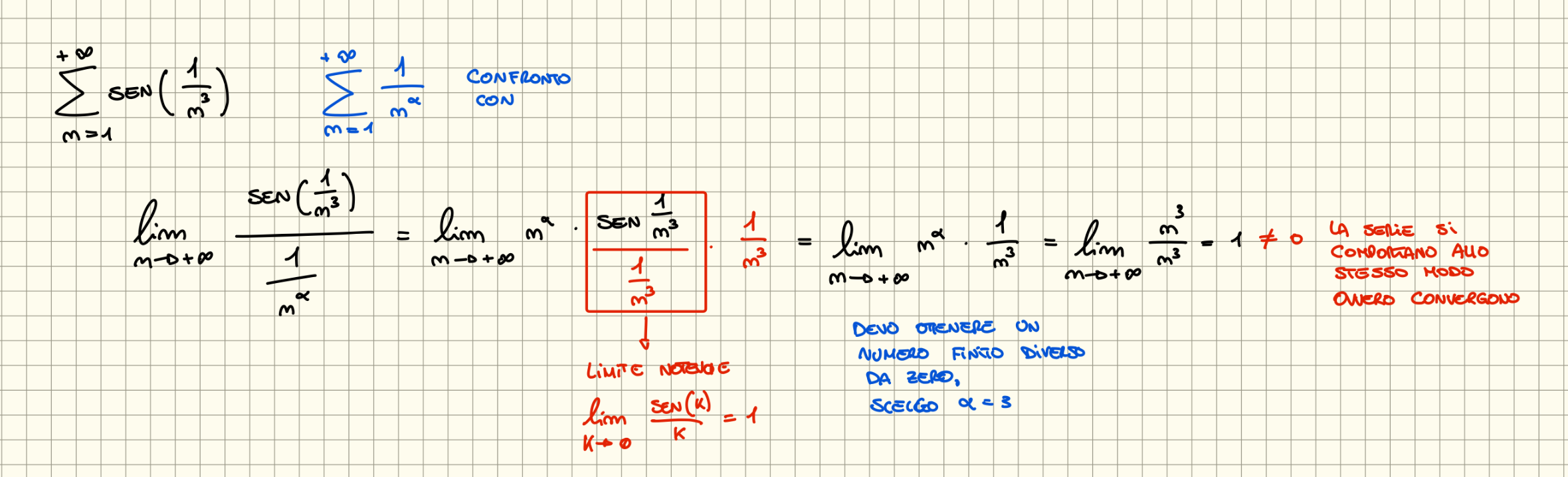
Criterio del Confronto Asintotico

Consideriamo la serie $\sum _{n=1}^{\infty }{a}_n$ e il limite $\underset{n\to +\infty }{\lim }{n}^{\alpha }{a}_n=l$

• Se con $a>1$ abbiamo $l\in \mathbb{R}$ allora la serie converge
• Se con $0<a\le 1$ e $l\ne 0$ oppure $l=+\infty$ allora la serie diverge

Siano $a_n,b_n\ge 0\forall n$, se $\underset{n\to +\infty }{\lim }\frac{a_n}{b_n}=l\in (0,+\infty )$ allora $\sum _{n=1}^{+\infty }{a}_n$ converge allora $\sum _{n=1}^{+\infty }{b}_n$ converge

Più nello specifico si comportano allo stesso modo, quindi se una converge o diverge allora anche l’altra. Quindi analizzando anche altri case, in fine otteniamo:

• Se $\underset{n\to +\infty }{\lim }\frac{a_n}{b_n}=l\in (0,+\infty )$ allora $\sum _{n=1}^{+\infty }{a}_n=\sum _{n=1}^{+\infty }{b}_n$
• Se $\underset{n\to +\infty }{\lim }\frac{a_n}{b_n}=0$ e se $\sum _{n=1}^{+\infty }{b}_n$ converge allora anche $\sum _{n=1}^{+\infty }{a}_n$ converge
• Se $\underset{n\to +\infty }{\lim }\frac{a_n}{b_n}=+\infty$ e se $\sum _{n=1}^{+\infty }{b}_n$ diverge allora anche $\sum _{n=1}^{+\infty }{a}_n$ diverge

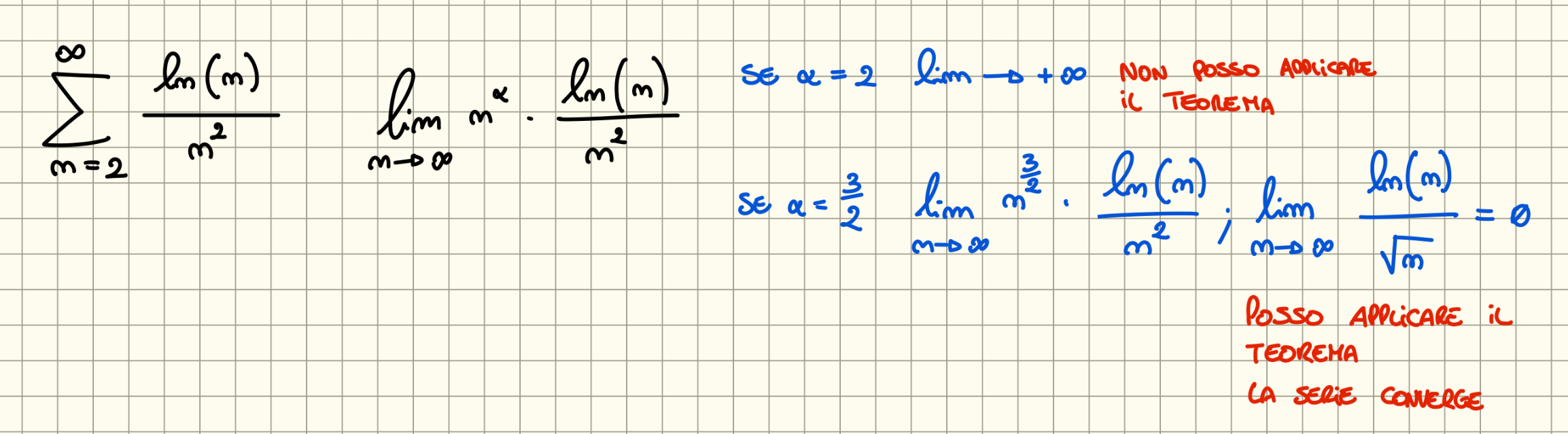
Serie a Termini Alterni

Una serie a termini alterni si comporta nel modo tipo $a_1-a_2+a_3-...+a_n$ ad esempio la serie:

$$\sum _{n=1}^{\infty }(-1{)}^{n+1}\cdot \frac{1}{n}=1-\frac{1}{2}+\frac{1}{3}-...$$

Per studiare questo tipo di serie si utilizza il Criterio di Leibniz

Criterio di Leibniz

La serie $\sum _{n=0}^{\infty }(-1{)}^n\cdot a_n$ converge se:

• $\underset{n\to \infty }{\lim }{a}_n=0$
• La successione dei valori assoluti $|a_1|,|a_2|,|a_n|$ deve essere decrescente e non obbligatoriamente dal primo termine

Convergenza Assoluta

Una serie a segno qualunque si dice che converge assolutamente quando la serie formata dai valori assoluti dei termini è convergente

Se una serie è assolutamente convergente allora la serie converge anche semplicemente, ma NON VALE IL CONTRARIO.

Serie Telescopiche

Prendiamo ad esempio la serie:

$$\sum _{n=1}^{+\infty }\frac{1}{n(n+1)}$$

Che può essere riscritta come:

$$\sum _{n=1}^{+\infty }\frac{1}{n}-\frac{1}{n+1}$$

Quindi otteniamo una somma come questa:

$$S_n=(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})+(\frac{1}{3}-\frac{1}{4})+...+(\frac{1}{n-1}-\frac{1}{n})+(\frac{1}{n}-\frac{1}{n+1})$$

Notiamo che ogni termine della successione si semplifica con il successivo lasciando soltanto primo ed ultimo termine quindi:

$$S_n=1-\frac{1}{n+1}$$

E calcolando il limite di $S_n$ per $n\to +\infty$ otteniamo $1$ e otteniamo quindi che

$$\sum _{n=1}^{+\infty }\frac{1}{n(n+1)}\text{ converge e la somma}$$

In Generale Una serie telescopia si calcola con la seguente forumula: $\sum _{n=1}^{+\infty }{b}_n-b_{n+1}=b_1-\underset{n\to +\infty }{\lim }{b}_{n+1}$

Serie Esponenziale

${\sum }_{k=0}^{+\infty }\frac{1}{k!}$

Posso utilizzare il criterio del rapporto e ottenere:

$$\begin{array}{r}\underset{k\to +\infty }{\lim }\frac{1}{(k+1)!}\cdot k!\to \frac{1}{k+1}=0\text{ Quindi la serie converge dato che }0<1\end{array}$$

Non lo dimostreremo ma nello specifico la serie $\sum _{k=0}^{+\infty }\frac{1}{k!}$ converge a $e$. Anche mettendo un numero al numeratore otterremo una serie convergente

$$\begin{array}{rl}& \sum _{k=0}^{+\infty }\frac{A^k}{k!}\\ & \underset{k\to +\infty }{\lim }\frac{A^{k+1}}{(k+1)!}\cdot \frac{k!}{A^k}\to \frac{A}{k+1}=0\text{ Quindi dato che 0 < 1 la serie converge}\end{array}$$

Formula Generale

${\sum }_{k=0}^{+\infty }\frac{A^k}{k!}=e^A$

Importante: Funziona anche con $A<0$ infatti con $\frac{|A^k|}{k!}$ possiamo utilizzare il criterio di Leibniz

Formula di Taylor

Grazie alla formula di Taylor possiamo approssimare delle funzioni tramite una funzione polinomiale più semplice.

Consideriamo una funzione definita in un intervallo $I$, $f(x):I$ e un punto $a\in I$, fissiamo ora un numero naturale $n\in \mathbb{N}$. Supponiamo adesso che la funzione sia derivabile $n-1$ volte in tutti i punti dell’intervallo e deve esistere almeno la derivate di ordine $n$ nel punto $a$.

Vogliamo determinare un polinomio $P_n$ di grado $n$ che calcolato nel punto $a$ sia uguale alla funzione calcolata nel punto $a$ e che la derivata prima del polinomio calcolata nel punto $a$ sia uguale alla derivata della funzione calcolata nel punto $a$. Così via per tutte le derivate, quindi:

$$P^{(n)}(a)=f^{(n)}(a)$$

Quindi il polinomio, in un intorno del punto $a$ approssimerà abbastanza bene la funzione

Il polinomio deve essere del tipo:

$$P_n(x)=c_0+c_1(x-a)+c_2(x-a{)}^2+...+c_n(x-a{)}^n$$

Calcoliamo ora le derivate:

$$\begin{array}{rl}& P^{\prime }(x)=c_1+2c_2(x-a)+...+c_n(x-a{)}^{n-1}\\ & P^{\prime \prime }(x)=2c_2+...+n(n-1)c_n(x-a{)}^{n-2}\\ & P^n(x)=n(n-1)(n-2)...1=n!\end{array}$$

Adesso se sostituiamo al posto di $x$ $a$ otteniamo che nelle parentesi abbiamo $0$

Quindi $P_n(a)=c_0=f(a)$, nel caso della derivata prima rimane soltanto $c_1$, $f^{\prime }(a)=c_1$ e così andando avanti $f^{\prime \prime }(a)=2c_2$, $f^{\prime \prime \prime }(a)=3\cdot 2\cdot c_3$.

Otteniamo quindi che:

$$\begin{array}{rl}& c_0=f(a)\\ & c_1=f^{\prime }(a)\\ & c_2=\frac{f^{\prime \prime }(a)}{2!}\\ & c_3=\frac{f^{\prime \prime \prime }(a)}{3!}\end{array}$$

Quindi come formula generale abbiamo:

$$P_n(x)=f(a)+\frac{f^{\prime }(a)}{1!}(x-a)+\frac{f^{\prime \prime }(a)}{2!}(x-a{)}^2+\frac{f^{\prime \prime \prime }(a)}{3!}(x-a{)}^3+\frac{f^{(n)}(a)}{n!}(x-a{)}^n$$

Esempio con funzione esponenziale $f(x)=e^{x}x=0$ approssimando fino al terzo grado

Quindi le derivate di 1,2 e 3 ordine sono la funzione stessa quindi otteniamo:

$$P_{n=3}=1+x+\frac{1}{2!}{x}^2+\frac{1}{3!}{x}^3$$

Sommatoria per Taylor

$\sum _{k=0}^n\frac{f^{(k)}(a)}{k!}(x-a{)}^k$

Calcolo delle derivate e principio di Sostituzione

Anche nelle serie di Taylor vale il principio di sostituzione quindi se ad esempio volessimo calcolare la serie di Taylor di $f(x)=e^{x^2}$ ci basterebbe porre $y=x^2$ e trasformare quindi la funzione in $f(x)=e^y$:

$$e^{x^2}=e^y=\sum _{k=0}^{\infty }\frac{y^k}{k!}=\sum _{k=0}^{\infty }\frac{(x^2{)}^k}{k!}=\sum _{k=0}^{\infty }\frac{x^{2k}}{k!}$$

Inoltre dato che il Polinomio di Taylor viene calcolato utilizzando le derivate della funzione è possibile calcolare il valore della derivata k-esima nel punto $x_0=0$ semplicemente calcolando il prodotto tra il termine $a_k$ della serie e $k!$

$$f^{(k)}=a_k\cdot k!$$

Esempio Consideriamo la funzione $f(x)=x^3\cdot sin(x^3)$, applichiamo per prima cosa il principio di sostituzione

$$\begin{array}{r}{x}^3\cdot sin(x^3)=y\cdot sin(y)=y\cdot \sum _{k=0}^{\infty }\frac{(-1{)}^k{y}^{2k+1}}{(2k+1)!}=\sum _{k=0}^{\infty }\frac{(-1{)}^k{y}^{2k+2}}{(2k+1)!}=\sum _{k=0}^{\infty }\frac{(-1{)}^k(x^3{)}^{2k+2}}{(2k+1)!}\\ =\sum _{k=0}^{\infty }\frac{(-1{)}^k{x}^{6k+6}}{(2k+1)!}\end{array}$$

Che una volta estesa è uguale a:

$$\frac{x^6}{1!}-\frac{x^{12}}{3!}+\frac{x^{18}}{5!}-\frac{x^{24}}{7!}+...=a_6{x}^6-a_{12}{x}^{12}+a_{18}{x}^{18}-a_{24}{x}^{24}+...$$

Quindi possiamo facilmente calcolare il valore delle derivate k-esime di $f(x)$:

• Valore di $f^{\prime \prime }(0)=a_2\cdot 2!=0$ Dato che il termine di grado 2 non esiste nella serie.
• Valore di $f^{(6)}(0)=a_6\cdot 6!=\frac{1}{1!}\cdot 6!=6!$
• Valore di $f^{(24)}(0)=a_{24}\cdot 24!=-\frac{1}{7!}\cdot 24!=-\frac{24!}{7!}$

Resto di Lagrange

Il polinomio di Taylor abbiamo detto che approssima la funzione, ma se aggiungiamo un termine complementare possiamo ottenere la funzione stessa, ovvero se abbiamo il polinomio di quinto grado dovremo aggiungere tutti i termini rimanenti dal sesto in poi.

$$f(x)=\sum _{k=0}^n\frac{f^{(k)}(a)}{k!}(x-a{)}^k+R_{n^x}$$

Iniziamo a definire questo resto che ci serve come complemento. Consideriamo di avere una funzione dipendente da una variabile $x$ definita in un intervallo $I$ e un punto $a$: $f(x):Ia$ e assumiamo che la funzione sia continua e derivabile $n$ volte in questo intervallo.

Adesso fissiamo un altro punto $x\in I$ e facciamo in modo che la derivata di ordine $n+1$ esista nei punti dell’intervallo $(a,x)$. Quindi:

$$\exists c\in (a,x)|f(x)=\sum _{k=0}^n\frac{f^{(k)}}{k!}(x-a{)}^k+\frac{f^{(n+1)}(c)}{(n+1)!}(x-a{)}^{n+1}$$

Non sappiamo chi sarà questo punto $c$ ma sappiamo solo che dipende dal punto iniziale $a$ e dall’ordine di derivazione, ma adesso mettiamoci nel caso $n=0$ e notiamo che:

$$\begin{array}{rl}& f(x)=f(a)+f^{\prime }(c)(x-a)\\ & f^{\prime }(c)=\frac{f(x)-f(a)}{x-a}\end{array}$$

Che non è altro che il Teorema di Lagrange

Serie di Potenze

Le serie di potenze hanno un insieme di convergenza ben definito e una struttura come questa:

$$\sum _{n=0}^{+\infty }{a}_n(x-x_0{)}^n=a_0+a_1(x-x_0)+a_2(x-x_0{)}^2+...+a_n(x-x_0{)}^n$$

Dove $x_0$ corrisponde al centro della serie. Il loro insieme di convergenza può essere chiuso o aperto anche solo in un estremo, può anche essere soltanto un punto o tutto $\mathbb{R}$.

Consideriamo ad esempio

$$\sum _{n=0}^{\infty }n!x^n$$

Ad esempio in $x=0$ la serie converge appunto a $0$ dato che stiamo moltiplicando ogni termine per $0$, ma se prendiamo qualsiasi altro $x$ la serie non converge più.

Altro esempio

$$\sum _{n=0}^{\infty }\frac{1}{n!}{x}^n$$

Questa serie invece converge qualsiasi sia il suo centro $x$.

Questi sono casi particolari, spesso troveremo serie di potenze dove l’insieme di convergenza è un intervallo

Insieme di Convergenza

Preso il centro della serie $x_0$ e presi due punti $x_0-R,x_0+R$ che definiranno l’intervallo prende il nome di raggio di convergenza il valore R($x_0+R-x_0$). L’intervallo può essere quindi di questo tipo:

• $(x_0-R,x_0+R)$
• $[x_0-R,x_0+R]$
• $(x_0-R,x_0+R]$
• $[x_0-R,x_0+R)$ Due serie possono avere lo stesso raggio di convergenza ma non per questo avranno lo stesso insieme di convergenza

Notiamo quindi che le serie di potenze convergono sempre nel loro centro

Come troviamo il Raggio di Convergenza? Utilizziamo la stessa relazione del criterio del rapporto

$$\underset{n\to +\infty }{\lim }|\frac{a_{n+1}}{a_n}|$$

A seconda del risultato abbiamo diversi casi:

• $l\ne 0\to R=\frac{1}{l}$
• $0\to R=+\infty$ La serie converge in qualsiasi intervallo
• $+\infty \to R=0$ Otteniamo quindi la convergenza in un solo punto (il centro)

Possiamo utilizzare anche un altro metodo ovvero il criterio della radice, utilizzando le stesse casistiche elencate sopra

Nel caso in cui $R=\frac{1}{l}$ abbiamo che nei punti interni all’intervallo $(x_0-R,x_0+R)$ abbiamo convergenza assoluta mentre nei punti esterni abbiamo divergenza $(-\infty ,x_0-R)(x_0+R,+\infty )$, ma cosa succede negli estremi? Può succedere qualsiasi cosa, quindi convergenza assoluta, convergenza oppure divergenza.

Quindi con una serie di potenze dobbiamo calcolare il suo raggio di convergenza per stabilire una prima parte dell’intervallo e poi, se necessario, studiare singolarmente gli estremi.

Funzioni Analitiche

Consideriamo di avere una serie di potenze:

$$\sum _{n=0}^{\infty }{a}_n(x-x_0{)}^n$$

Come sappiamo una serie di potenze ha un insieme di convergenza, comprende sempre il centro e di solito è un intervallo di valori. In questo caso abbiamo come centro $x_0$

In questo intervallo di convergenza diciamo che la nostra serie converge ad una funzione $f(x)$.

Adesso consideriamo il problema inverso

Abbiamo una funzione $f(x):I(x_0)$ definita in un intervallo di $x_0$ e ci chiediamo se è possibile scrivere questa funzione come serie di potenze.

Abbiamo una condizione da rispettare affinché si verifichi questa cosa:

• La funzione, in ogni punto dell’intervallo deve essere derivabile infinite volte

In questo modo posso scrivere lo sviluppo di Taylor della funzione e notare che rispetta la forma delle serie di potenze

$$f(x_0)+\frac{f^{\prime }(x_0)}{1!}(x-x_o)+\frac{f^{\prime \prime }(x_0)}{2!}(x-x_0{)}^2+\dots +\frac{f^{(n)}(x_0)}{n!}(x-x_0{)}^n$$

Dobbiamo porci delle domande però:

• Questa serie di potenze converge sempre nell’intorno I?
• E se converge, la somma di questa serie è uguale a $f(x)$?

Non accade sempre, esiste quindi una condizione da soddisfare?

Si, tutte le derivate devono essere limitate.

Condizioni per rappresentare una funzione come serie di potenze

Data $f(x):I(x_0)$ derivabile infinite volte nell’intervallo, deve $\exists M>0\text{ tale che }|f^{(n)}(x)|\le M$, con queste condizioni $\sum _{n=0}^{\infty }{a}_n(x-x_0{)}^n=f(x)$ Quindi una funzione si dice analitica quando è scrivibile come serie di potenze e quando quest’ultima è uguale alla funzione stessa

Esempi Consideriamo la funzione $f(x)=sen(x)$, esiste una serie di potenze centrata in 0, $x=0$, tale che la somma della serie di potenze, in un determinato intervallo, è uguale a $sen(x)$. Come sappiamo la funzione seno è derivabile infinite volte in ogni punto e le sue derivate sono sempre limitate dato che alterniamo seni e coseni, quindi questa funzione è sicuramente scrivibile come serie di potenze.

$$sen(x)=\sum _{n=0}^{\infty }\frac{(-1{)}^n}{(2n+1)!}{x}^{2n+1}$$

---

$$e^x=\sum _{n=0}^{\infty }\frac{x^n}{n!}=1+\frac{1}{1!}x+\frac{1}{2!}{x}^2+\dots +\frac{1}{n!}{x}^n$$

---

Serie Notevoli

$$\begin{array}{rl}& sin(x)=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\dots =\sum _{n=0}^{\infty }\frac{(-1{)}^n}{(2n+1)!}{x}^{2n+1}\\ & \\ & cos(x)=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\dots =\sum _{n=0}^{\infty }\frac{(-1{)}^n}{(2n)!}{x}^{2n}\\ & \\ & e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\dots =\sum _{n=0}^{\infty }\frac{x^n}{n!}\\ & \\ & \ln (1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+\dots =\sum _{n=1}^{\infty }(-1{)}^{n+1}\frac{x^n}{n}|x|<1\\ & \\ & \frac{1}{1-x}=1+x+x^2+x^3+x^4+\dots =\sum _{n=0}^{\infty }{x}^n|x|<1\\ & \\ & \frac{1}{1+x^2}=1-x^2+x^4-x^6+\dots =\sum _{n=0}^{\infty }(-1{)}^n{x}^{2}n|x|<1\end{array}$$

Limiti Notevoli

$$\begin{array}{rl}& \underset{n\to \infty }{\lim }{\left(1+\frac{A}{n}\right)}^n=e^A\\ & \\ & \underset{n\to 0}{\lim }(e^n-1)=0e^n-1\approx n\\ & \\ & \underset{n\to 0}{\lim }\ln (1+n)=0\ln (1+n)\approx n\\ & \\ & \underset{n\to 0}{\lim }\sin (n)=0\sin (n)\approx n\\ & \\ & \underset{n\to 0}{\lim }\tan (n)=0\tan (n)\approx n\\ & \\ & \underset{n\to 0}{\lim }\arcsin (n)=0\arcsin (n)\approx n\\ & \\ & \underset{n\to 0}{\lim }\arctan (x)=0\arctan (n)\approx n\\ & \\ & \underset{n\to 0}{\lim }1-\cos (n)=0\frac{1-\cos (n)}{n^2}=\frac{1}{2};1-\cos (n)\approx \frac{n^2}{2}\end{array}$$