Derivate

Sia $f:[a,b]\to \mathbb{R},x_0\in (a,b)$ Se $\exists {\lim }_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}=L\in \mathbb{R}$ Allora $f$ si dice derivabile in $x_0$ e $L=f^{\prime }(x_0)$ si chiama derivata prima di $f(x)$ in $x_0$

Formule

• $[x^n{]}^{\prime }=n{x}^{n-1}\forall xn\in \mathbb{N}$
• $[e^{f(x)}{]}^{\prime }=e^{f(x)}\ast f^{\prime }(x)\forall x$
• $[log(x){]}^{\prime }=\frac{1}{x}x>0$
• $[sen(x){]}^{\prime }=cos(x)\forall x$
• $[cos(x){]}^{\prime }=-sen(x)\forall x$
• $[tg(x){]}^{\prime }=\frac{1}{co{s}^2(x)}\forall x\ne \frac{\pi }{2}+k\pi$
• $[x^{\alpha }{]}^{\prime }=\alpha x^{\alpha -1}x>0\alpha \in \mathbb{R}$
• $[arctg(x){]}^{\prime }=\frac{1}{x^2+1}\forall x$
• $[arcsen(x){]}^{\prime }=\frac{1}{\sqrt{1-x^2}}|x|<1$
• $[arccos(x){]}^{\prime }=-\frac{1}{\sqrt{1-x^2}}|x|<1$

Derivate composte

• $[f(x)\pm g(x){]}^{\prime }=f^{\prime }(x)\pm g^{\prime }(x)$
• $[f(x)\ast g(x){]}^{\prime }=f^{\prime }(x)g(x)+f(x)g^{\prime }(x)$
• $[\frac{f(x)}{g(x)}{]}^{\prime }=\frac{f^{\prime }(x)g(x)-f(x)g^{\prime }(x)}{[g(x){]}^2}$

Quindi se una funzione è derivabile in punto significa che in quello stesso punto è anche continua, ma è vero anche il viceversa? Prendiamo come esempio la funzione $f(x)=|x|$ Calcoliamo il rapporto incrementale in $x=0$ Possiamo notare lo stesso risultato anche con la funzione $f(x)=\sqrt[3]{x}$

Utilizzi delle derivate

• Con le derivate si studia la monotonia di una funzione
• Con le derivate si trovano massimi e minimi
• Con le derivate si approsimano le funzioni con polinomi

Teorema di Lagrange

Sia $f:[a,b]\to \mathbb{R}$ continua in $[a,b]$ e derivabile in $(a,b)$ allora esiste $c\in (a,b)$: $f^{\prime }(c)=\frac{f(b)-f(a)}{b-a}$ Il teorema ci dice quindi che sotto le ipotesi di continuità e derivabilità, esiste almeno un punto $c$ interno all’intervallo tale che la derivate prima valutata in tale punto valga quanto il rapporto tra la differenza delle ordinate e la differenza delle ascisse agli estremi dell’intervallo.

Funzione crescente e decrescente

$f(x)\text{e’ crescente se}\frac{f(x)-f(y)}{x-y}\ge 0$ $f(x)\text{e’ decrescente se}\frac{f(x)-f(y)}{x-y}\le 0$ Entrambe: $\forall x\ne y\in [a,b]$

Quindi:

Esercizio

Quindi: $f(x)$ cresce su $(-\infty ,1]$ $f(x)$ decresce su $[1,2]$ $f(x)$ cresce su $[2,+\infty )$

Punti di massimo e minimo

Sia $f:[a,b]\to \mathbb{R}$, e sia $x_0\in (a,b)$

$x_0$ si dice di massimo relativo per $f(x)$ se $\exists \delta \ge 0:f(x_0)\ge f(x)\forall x\in [x_0-\delta ,x_0+\delta ]$

$x_0$ si dice di minimo relativo per $f(x)$ se $\exists \delta \ge 0:f(x_0)\le f(x)\forall x\in [x_0-\delta ,x_0+\delta ]$

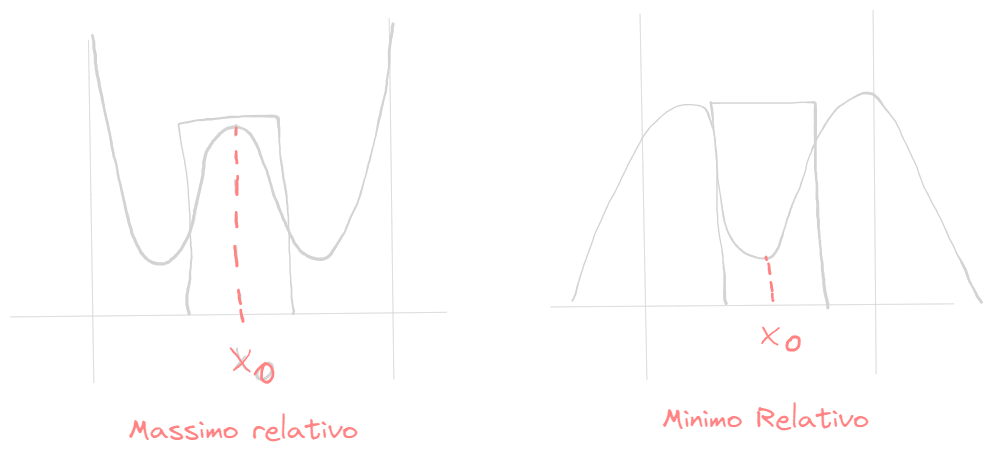
Trovare massimi e minimi

Nella funzione usata precedentemente come esercizio avevamo i punti 1,2 per sapere se sono massimi o minimi ci basta vedere se la derivata in quel punto vale 0

Se $x_0$ e’ un massimo/minimo relativo allora $f^{\prime }(x_0)=0$

Trovare massimi e minimi assoluti

Data una funzione $f:[a,b]\to \mathbb{R}$ per trovare massimi e minimi assoluti dobbiamo considerare tre insiemi:

• $A=\{a,b\}$
• $B=\{x\in (a,b):f^{\prime }(x)=0\}$
• $C=\{x\in (a,b):\text{non esiste}{f}^{\prime }(x)\}$

Calcoliamo $f(x)$ in ogni punto di questi insiemi e il maggiore sarà il massimo assoluto mentre il minore il minimo assoluto Esempio:

Esercizio

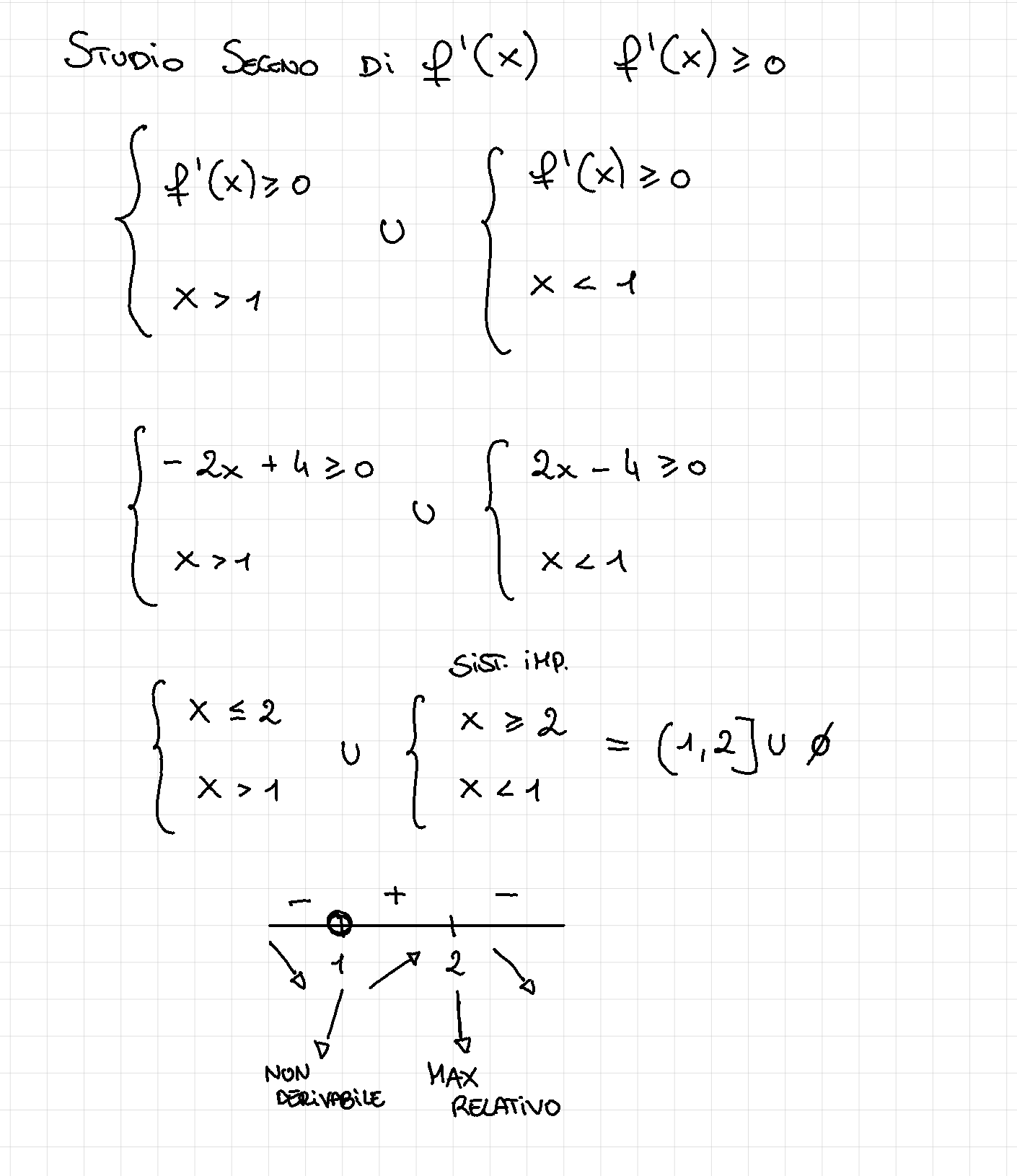
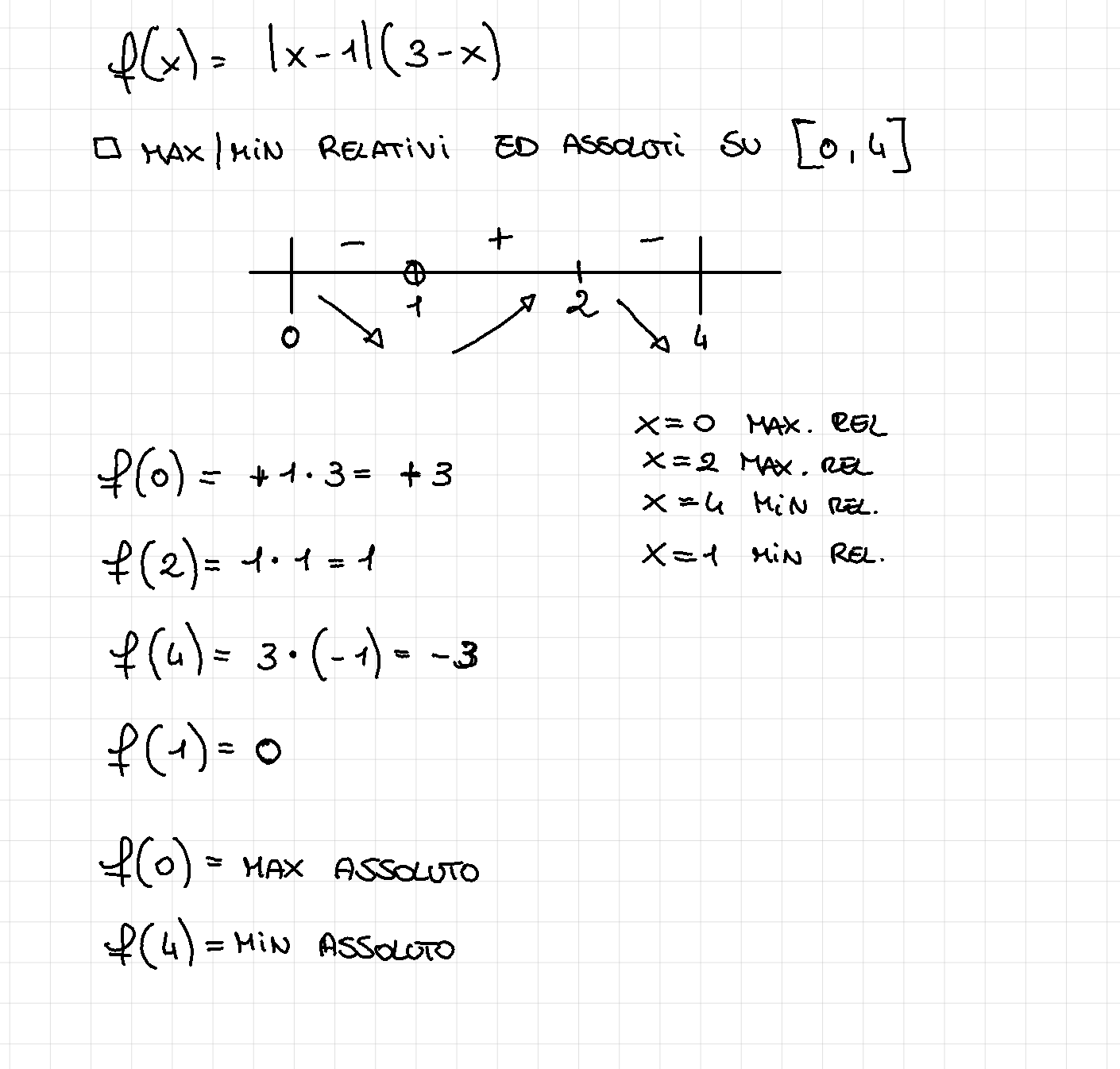
Problemi di ottimizzazione: