Integrali

Gli integrali ci tornano utili al calcolo delle aree dei trapezoidi.

Supponiamo ci venga assegnata una certa funzione $f(x)$ e un intervallo $[a,b]$ sull’asse delle $x$. Possiamo considerare integrale della funzioen $f(x)$ nell’intevallo $[a,b]$ l’area di piano:

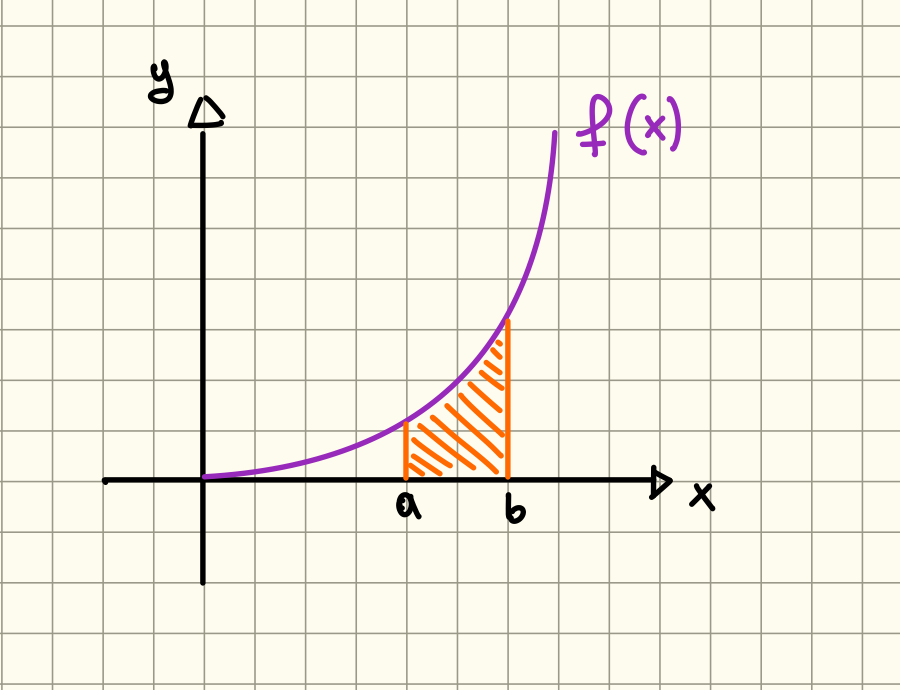
Definizione non formale

${\int }_a^{b}f(x)dx=$ Area con segno della regione di piano compresa tra il grafico di $f(x)$, l’asse delle $x$ e le rette verticali $x=a,x=b$. La definiamo area con segno perché se il grafico fosse sotto l’asse delle $x$ l’area, o meglio l’integrale, sarebbe negativo.

Notazioni

L’intervallo $[a,b]$ prende il nome di intervallo (zona) di integrazione mentre la funzione $f(x)$ si chiama funzione integranda, il dx ci indica che stiamo integrando rispetto alla variabile x.

Vediamo ora come definirlo in modo più preciso.

Prendiamo una funzione costante $k$ al posto di $f(x)$:

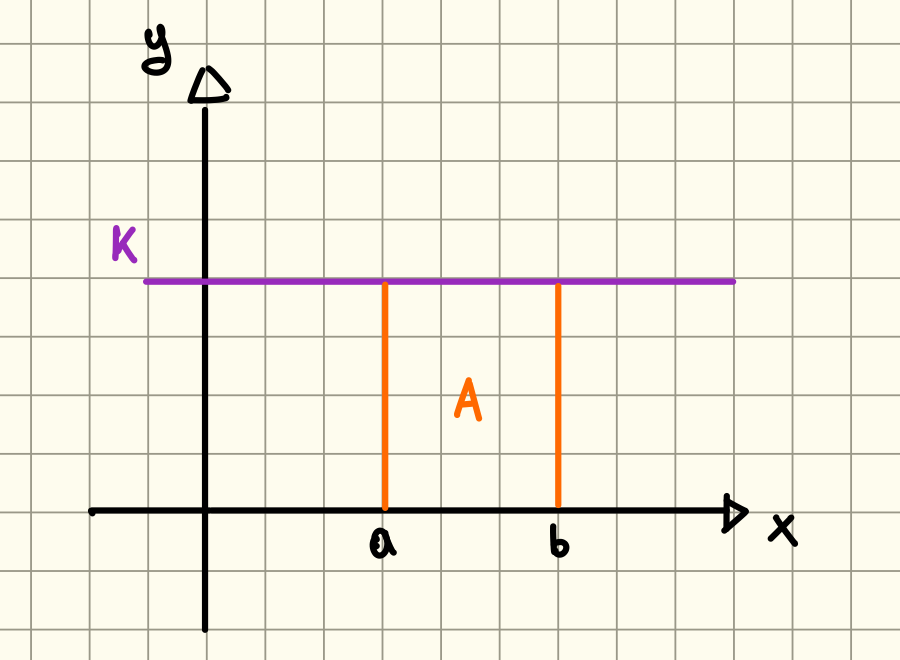
Sia $f(x)=k\forall x\in [a,b]$, con $k$ costante reale allora l’integrale di $f$ sull’intervallo $[a,b]$ è:

$${\int }_a^{b}f(x)dx=(b-a)\cdot k=\text{ area (con segno) del rettangolo}$$

Dove $(b-a)$ indica la base e $k$ l’altezza (con segno).

Definire l’integrale diventa leggermente più complesso con le funzioni definite a tratti, ad esempio:

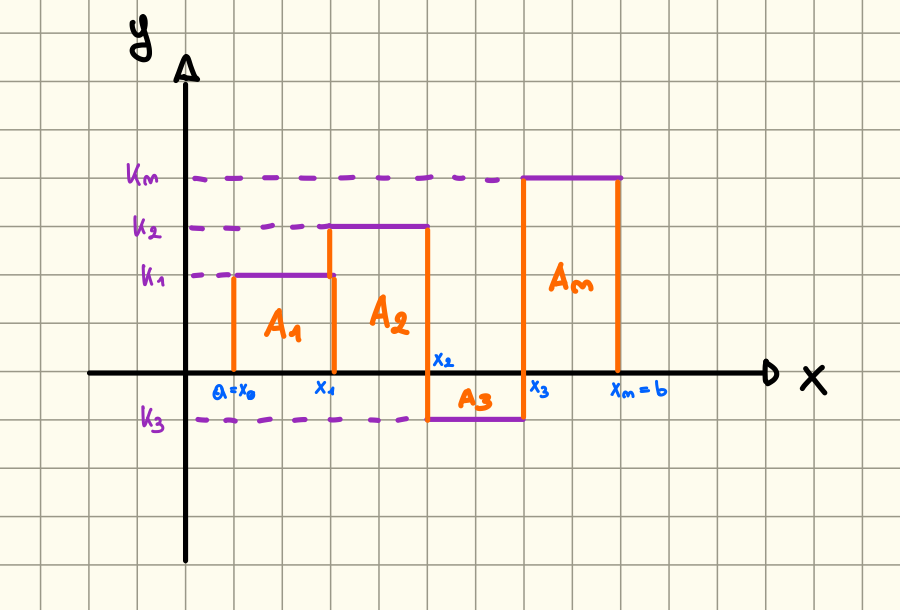
In questo caso l’integrale viene definito come la somma algebrica delle aree (con segno) dei rettangoli.

Quindi: Sia $f(x)$ una funzione a scala ovvero che assume il valore $k_i$ nell’i-esimo intervallo avente $x_{i-1}$ ed $x_i$ come estremi allora l’integrale di $f$ sull’intervallo $[a,b]$ è:

$${\int }_a^{b}f(x)dx=\sum _{i=1}^n(x_i-x_{i-1})\cdot k_i=\text{somma algebrica delle aree dei rettangoli}$$

---

Vediamo adesso cosa succede con una funzione non costante, quindi un’area simile a questa:

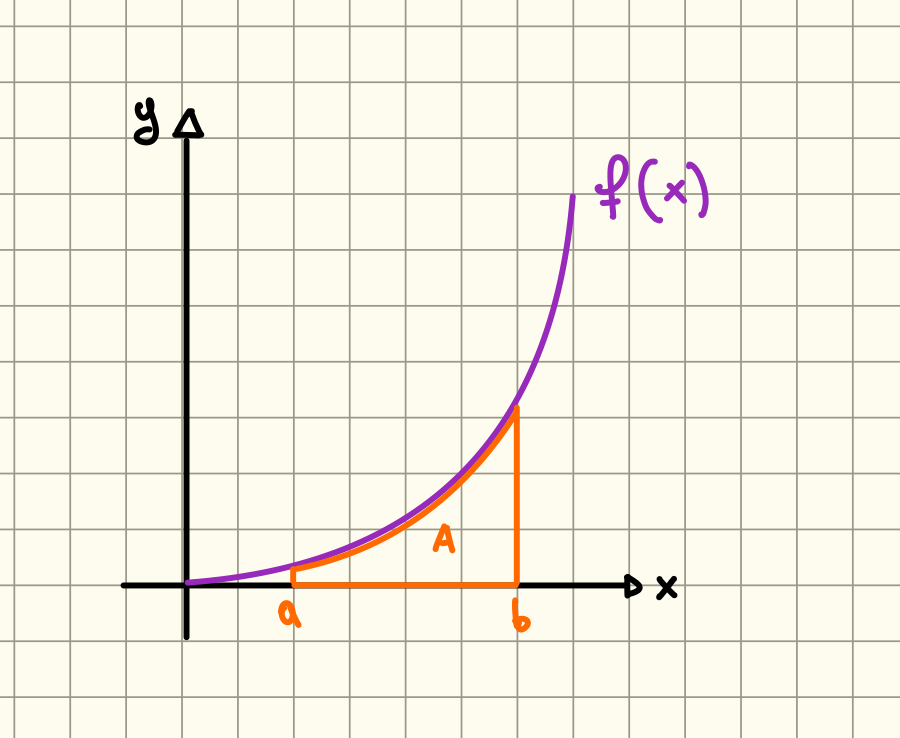
L’idea è quella di considerare delle funzioni a scala che siano sempre maggiori o uguali della nostra funzione $f(x)$:

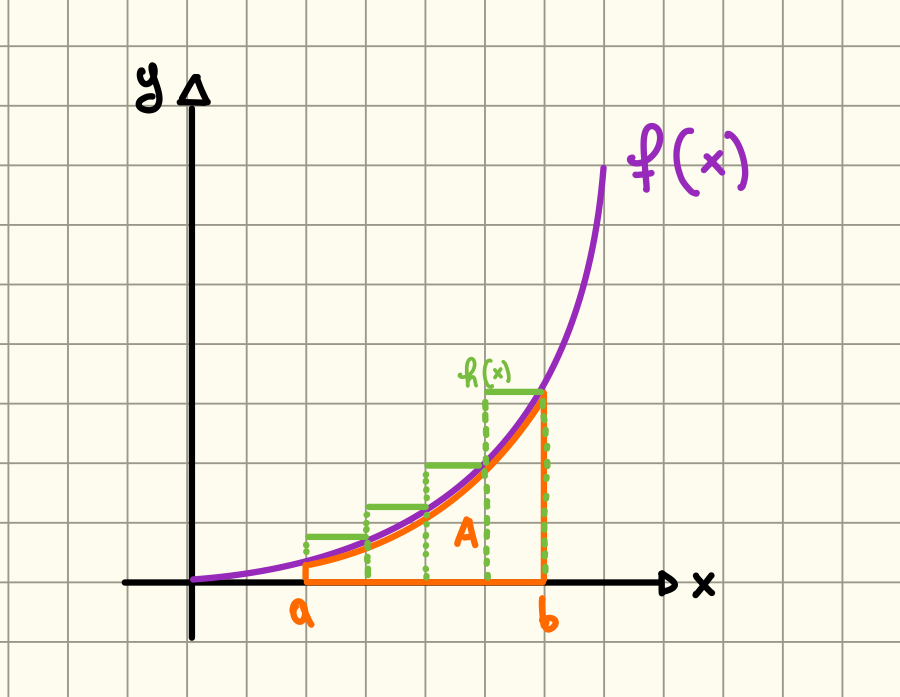
In questo modo possiamo approssimare l’integrale della funzione $f(x)$ con l’integrale della funzione scalare $h(x)$ che sappiamo come calcolare.

Quindi:

$$A\le {\int }_a^{b}h(x)dx$$

Ovviamente di funzioni scalari maggiori o uguali della nostra $f(x)$ ne esistono infinite e molte di queste approssimano meglio il valore dell’integrale, infatti ci basta prendere rettangoli più piccoli in modo da ridurre l’errore dell’approssimazione.

Quindi se consideriamo l’insieme degli integrali di queste funzioni, l’estremo inferiore di questo insieme coincide con l’area che vogliamo calcolare

$$A\le \inf \left\{{\int }_a^{b}h(x)dx:h(x)\text{ a scala e }h(x)\ge f(x)\forall x\in [a,b]\right\}$$

Possiamo anche considerare delle funzioni $g(x)$ che invece approssimano la funzione $f(x)$ ma per difetto e ragionare allo stesso modo:

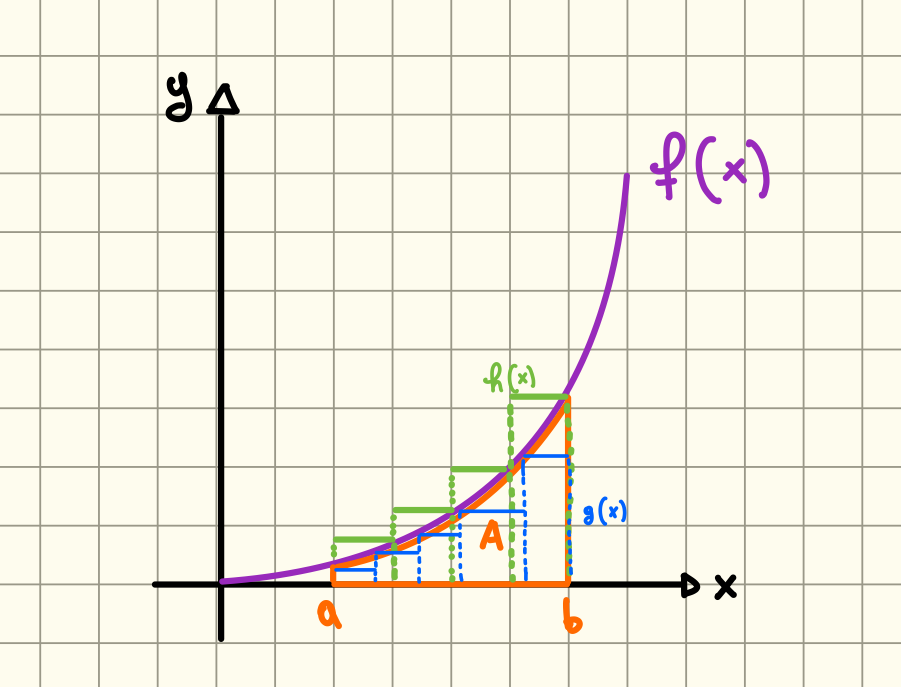
Quindi in questo caso consideriamo l’estremo superiore dell’insieme degli integrali di queste funzioni e possiamo quindi dire che la nostra area A è compresa tra i due estremi:

$$\sup \left\{{\int }_a^{b}g(x)dx:\begin{array}{rl}& g(x)\text{ a scala e}\\ & g(x)\le f(x)\forall x\in [a,b]\end{array}\right\}$$ $$\inf \left\{{\int }_a^{b}h(x)dx:\begin{array}{rl}& h(x)\text{ a scala e }\\ & h(x)\ge f(x)\forall x\in [a,b]\end{array}\right\}$$ $$\sup (\cdots )\le A\le \inf (\cdots )$$

Se questi due valori coincidono, si dice che $f$ è Riemann Integrabile sull’intervallo $[a,b]$ ed il valore comune è ${\int }_a^{b}f(x)dx$

Come si calcolano gli Integrali

Per calcolare ${\int }_a^{b}f(x)dx$ dobbiamo:

• Trovare una funzione che nell’intervallo $[a,b]$ abbiamo $f(x)$ come derivata, questa prende il nome di primitiva di $f$
• Calcoliamo questa funzione negli estremi della zona di integrazione
• Calcoliamo la differenza $F(b)-F(a)$

Esempio

$${\int }_0^{5}3x^{2}dx$$

Come primitiva possiamo prendere $x^3$, quindi:

$$\begin{array}{rl}& F(b)=5^3=125\\ & F(a)=0^3=0\\ & \\ & {\int }_0^{5}3x^{2}dx=[x^3{]}_0^5=125-0=125\end{array}$$

Primitive Elementari e Proprietà degli Integrali

Prima di calcolare le primitive di una funzione dobbiamo chiederci se questa ammette primitive nell’intervallo di integrazione.

Funzione che ammette primitive

Ogni funzione $f:[a,b]\to \mathbb{R}$ continua ammette delle primitive. La primitiva di una funzione non è mai unica infatti se $F(x)$ è una primitiva lo è anche $F(x)+c$ con $c\in \mathbb{R}$ costante

Per indicare una generica primitiva di $f(x)$ si può anche utilizzare la notazione:

$$\int f(x)dx$$

Detto anche integrale indefinito di $f(x)$

Primitive Elementari

$f(x)$	$F(x)$
$\cos (x)$	$\sin (x)$
$\sin (x)$	$-\cos (x)$
$e^x$	$e^x$
$a^x$	$\frac{a^x}{\ln (a)}$
$x^n$	$\frac{x^{n+1}}{n+1}\forall n\ne -1$
$\frac{1}{x}$	$\ln (\Vert x\Vert )$
$\frac{1}{1+x^2}$	$\arctan (x)$

Proprietà dell’integrale

Linearità

$${\int }_a^{b}f(x)\pm g(x)dx={\int }_a^{b}f(x)dx\pm {\int }_a^{b}g(x)dx$$

Additività

$\forall a\le c\le b$

$${\int }_a^{b}f(x)dx={\int }_a^{c}f(x)dx+{\int }_c^{b}f(x)dx$$

Disuguaglianza Triangolare

$$\left|{\int }_a^{b}f(x)dx\right|\le {\int }_a^b\left|f(x)\right|dx$$

Costante Moltiplicativa

$$\int kf(x)dx=k\int f(x)dx$$

Esempio

$$\begin{array}{rl}\int (3x+\cos (x))dx& =\int 3xdx+\int \cos (x)dx\\ & =3\int xdx+\int \cos (x)dx=3\frac{x^2}{2}+\sin (x)+c\end{array}$$

NOTA

Queste proprietà possono essere utilizzate allo stesso modo sia per integrali definiti che non definiti.

Integrali di Derivate di Funzioni Composte

Ricordiamo la regola di derivazione delle funzioni composte:

$${\left[F(g(x))\right]}^{\prime }=f(g(x))\cdot g^{\prime }(x)$$

Dove $F$ indica una primitiva di $f$, se quindi integriamo il risultato dovremmo ottenere la funzione iniziale:

$$\int f(g(x))\cdot g^{\prime }(x)dx=F(g(x))+c$$

Con questa formula possiamo risolvere molti integrali, esempio:

$$\int 3x^2\sin (x^3)dx=-\cos (x^3)+c$$

Infatti abbiamo che:

$$g^{\prime }(x)=3x^2\text{ mentre }f(g(x))=\sin (x^3)$$

Esempio 2:

$$\int e^{\sin (x)}\cos (x)dx=e^{\sin (x)}+c$$

Esempio 3:

$$\int x(x^2-1{)}^{2014}dx$$

In questo caso abbiamo:

$$f(g(x))=(x^2-1{)}^{2014}\text{ mentre }{g}^{\prime }(x)=2x$$

Notiamo quindi che all’interno dell’integrale non appare la derivate prima di $g(x)$, possiamo però farla comparire aggiustando l’integrale con delle costanti moltiplicative:

$$\int x(x^2-1{)}^{2014}dx=\frac{1}{2}\int 2x(x^2-1{)}^{2014}=\frac{1}{2}\cdot \frac{(x^2-1{)}^{2015}}{2015}+c=\frac{(x^2-1{)}^{2015}}{4030}+c$$

Possiamo quindi generalizzare la tabella delle primitive:

Primitive Elementari	Primitive Elementari Generalizzate
$\int \cos (x)dx=\sin (x)+c$	$\int f^{\prime }(x)\cos [f(x)]dx=\sin [f(x)]+c$
$\int \sin (x)dx=-\cos (x)+c$	$\int f^{\prime }(x)\sin [f(x)]dx=-\cos [f(x)]+c$
$\int e^{x}dx=e^x+c$	$\int f^{\prime }(x)e^{f(x)}dx=e^{f(x)}+c$
$\int x^{n}dx=\frac{x^{n+1}}{n+1}+c(n\ne -1)$	$\int f^{\prime }(x)[f(x){]}^{n}dx=\frac{[f(x){]}^{n+1}}{n+1}+c$
$\int \frac{1}{x}dx=\ln (\Vert x\Vert )+c$	$\int \frac{f^{\prime }(x)}{f(x)}dx=\ln (\Vert f(x)\Vert )+c$
$\int a^{x}dx=\frac{a^x}{\ln (a)}+c$	$\int f^{\prime }(x)a^{f(x)}=\frac{a^{f(x)}}{\ln (a)}+c$

• Derivate e Integrali Fondamentali

Esempio 4:

$$\int \frac{\cos x}{\sin x}dx=\ln |\sin x|+c$$

È importante ricordare che non tutti gli integrali sono facilmente riconducibili a primitive elementari ma ci sarà bisogno di utilizzare altre tecniche di integrazione.

Integrazione per Parti

L’integrazione per parti ci consente di integrare le funzioni che si presentano nel seguente modo:

$$\int f(x)g^{\prime }(x)dx=f(x)g(x)-\int f^{\prime }(x)g(x)dx$$

Ovviamente questa formula non risolve immediatamente l’integrale ma ci aiuta nel caso in cui il secondo integrale trovato sia più semplice da risolvere

Esempio 1

$$\begin{array}{rl}& \int x\cos (x)dx\\ & \\ & \text{Possiamo scegliere }f(x)=x,g^{\prime }(x)=\cos (x)\\ & \\ & =x\sin (x)-\int 1\cdot (\sin (x))dx=x\sin (x)+\cos (x)+c\end{array}$$

Esempio 2

$$\begin{array}{rl}& \int x{e}^{x}dx\\ & \\ & \text{Possiamo scegliere come }f(x)=x,g^{\prime }(x)=e^x\\ & \\ & =x{e}^x-\int e^x=x{e}^x-e^x+c\end{array}$$

Esempio 3

$$\begin{array}{rl}& \int x^2{e}^{x}dx\\ & \\ & \text{Possiamo scegliere }f(x)=x^2,g^{\prime }(x)=e^x\\ & \\ & =x^2{e}^x-\int 2x{e}^x=x^2{e}^x-2\int x{e}^x\\ & \\ & \text{Questo secondo integrale possiamo risolverlo nuovamente per parti}\\ & \text{eˋ infatti l’esempio precedente}\\ & \\ & =x^2{e}^x-2(x{e}^x-e^x)+c\end{array}$$

Tutti gli integrali visti in questi esempi che sono del tipo:

$$\int x^{\alpha }{e}^{x}dx;\int x^{\alpha }\cos (x)dx;\int x^{\alpha }\sin (x)dx$$

Si risolvono come abbiamo visto prima applicando più volte l’integrazione per parti. Vediamo ora una nuova tipologia con i polinomi

Esempio 4

$$\begin{array}{rl}& \int (x^4+3x^2-6)e^{x}dx\\ & \\ & \text{Possiamo spezzare l’integrale in piuˋ integrali}\\ & \\ & \int x^4{e}^{x}dx+\int 3x^2{e}^{x}dx+\int -6e^{x}dx=\\ & \\ & =\int x^4{e}^{x}dx+3\int x^2{e}^{x}dx-6\int e^{x}dx\end{array}$$

I primi due integrali possiamo risolverli per parti come abbiamo fatto prima mentre l’ultimo è immediato. Quindi sappiamo risolvere tutti gli integrali del tipo:

$$\int p(x)e^{x}dx;\int p(x)\cos (x)dx;\int p(x)\sin (x)dx$$

Esempio 5

$$\begin{array}{rl}& \int x\log (x)dx\\ & \\ & \text{In questo caso ci conviene scegliere }{g}^{\prime }(x)=x,f(x)=\ln (x)\\ & \\ & =\frac{x^2}{2}\cdot \ln (x)-\int \frac{1}{x}\cdot \frac{x^2}{2}dx=\\ & \frac{x^2}{2}\cdot \ln (x)-\int \frac{x}{2}dx=\frac{x^2}{2}\cdot \ln (x)-\frac{1}{2}\cdot \frac{x^2}{2}=\frac{x^2}{2}\cdot \ln (x)-\frac{x^2}{4}+c\end{array}$$

Integrazione per Parti: Fattore differenziale 1 e Integrali Ciclici

Iniziamo vedendo il “trucco” della moltiplicazione per 1 con un esempio:

Esempio 1

$$\begin{array}{rl}& \int \ln (x)dx=\int 1\cdot \ln (x)dx\\ & \\ & \text{Possiamo scegliere }f(x)=\ln (x);g^{\prime }(x)=1\\ & \\ & =\ln (x)\cdot x-\int \frac{1}{x}\cdot xdx=\ln (x)\cdot x-x+c\end{array}$$

Esempio 2

$$\begin{array}{rl}& \int \arctan (x)dx=\int \arctan (x)\cdot 1dx\\ & \\ & \text{Scegliamo come }f(x)=\arctan (x);g^{\prime }(x)=1\\ & \\ & \arctan (x)\cdot x-\int \frac{x}{1+x^2}\cdot dx\\ & \\ & \text{Possiamo rendere il secondo integrale immendiato con una costante}\\ & \\ & =\arctan (x)\cdot x-\frac{1}{2}\int \frac{2x}{1+x^2}dx=\arctan (x)\cdot x-\frac{1}{2}\cdot \ln (|1+x^2|)+c\end{array}$$

Vediamo un esempio più particolare:

Esempio 3

$$\int xdx$$

Che è risolvibile immediatamente, ma cosa succede se lo risolviamo con l’integrazione per parti?

$$\int xdx=\int 1\cdot xdx=x^2-\int xdx$$

Notiamo che ritorniamo alla situazione iniziale e che l’integrale è uguale a qualcosa meno se stesso. Quindi se portiamo il risultato a sinistra dell’uguale otteniamo:

$$2\int xdx=x^2;\int xdx=\frac{x^2}{2}+c$$

Questo tipo di integrali che riappaiono con un - davanti nella loro scomposizione per parti prendono il nome di integrali ciclici. In questi casi prendiamo questo integrale, lo portiamo a sinistra nella catena delle uguaglianze svolgendo la somma e risolviamo.

Esempio 4

$$\begin{array}{rl}& \int {\cos }^2(x)dx=\int \cos (x)\cdot \cos (x)dx\\ & \\ & \text{Impostiamo }f(x)=\cos (x);g^{\prime }(x)=\cos (x)\\ & \\ & \cos (x)\cdot \sin (x)-\int -{\sin }^2(x)=\cos (x)\cdot \sin (x)+\int {\sin }^2(x)\\ & \\ & =\cos (x)\cdot \sin (x)+\int 1-{\cos }^2(x)dx=\cos (x)\cdot \sin (x)+x-\int {\cos }^2(x)dx\\ & \\ & \text{Quindi portandolo a sinistra}\\ & \\ & 2\int {\cos }^2(x)dx=\sin (x)\cdot \cos (x)+x=\frac{\sin (x)\cdot \cos (x)+x}{2}+c\end{array}$$

Integrazione per Sostituzione

La formula che si usa per l’integrazione tramite sostituzione è la seguente:

$${\int }_a^{b}f(g(x))g^{\prime }(x)dx={\int }_{g(a)}^{g(b)}f(y)dy$$

Esempio

$$\begin{array}{rl}& \int \sin (e^x)e^{x}dx\\ & \\ & \text{Effettuiamo queste sostituzione }y=e^x;dy=e^{x}dx\\ & \text{Nella sostituzione di dy dobbiamo scrivere la derivate * dx}\\ & \\ & =\int \sin (y)dy=-\cos (y)+c=-\cos (e^x)+c\end{array}$$

Quindi la regola per effettuare la sostituzione è:

$$y=g(x)dy=g^{\prime }(x)dx$$

E nel caso di integrali definiti al posto degli estremi avremo:

$$a=g(a)b=g(b)$$

Esempio 2

$$\begin{array}{rl}& \int \cos (x)\cdot \sin (\sin (x))dx\\ & \\ & y=\sin (x)dy=\cos (x)dx\\ & \\ & \int \sin (y)dy=-\cos (y)+c=-\cos (\sin (x))+c\end{array}$$

Esempio 3

$$\begin{array}{rl}& {\int }_0^{\sqrt{\pi }}x\cos (x^2)dx\\ & \\ & y=x^{2}dy=2xdx0\to 0^2=0\sqrt{\pi }\to (\sqrt{\pi }{)}^2=\pi \\ & \\ & {\int }_0^{\pi }\cos (y)\frac{dy}{2}=\frac{1}{2}{\int }_0^{\pi }\cos (y)dy=\frac{1}{2}[\sin (y){]}_0^{\pi }\\ & \\ & =\frac{1}{2}(\sin (\pi )-\sin (0))=0\end{array}$$

Integrazione di Funzioni Razionali

Si tratta di integrare funzioni del tipo

$$f(x)=\frac{P(x)}{Q(x)}\text{ con P(x) e Q(x) polinomi e }Q(x)\ne 0$$

Caso Semplice Nel caso in cui $P(x)$ è la derivata di $Q(x)$ possiamo risolvere immediatamente l’integrale:

$$\int \frac{f^{\prime }(x)}{f(x)}dx=\ln |f(x)|+c$$

Esempio 1

$$\int \frac{2x}{x^2+5}dx=\ln |x^2+5|+c$$

Esempio 2

$$\int \frac{x^3}{x^4+1}dx=\frac{1}{4}\int \frac{4x^3}{x^4+1}=\frac{1}{4}\cdot \ln |x^4+1|+c$$

Caso 2 In questo caso abbiamo al numeratore una costante e al denominatore un polinomio di primo grado. Utilizziamo un metodo risolutivo simile al precedente

Esempio 3

$$\int \frac{3}{2x-1}dx=\frac{3}{2}\int \frac{2}{2x-1}=\frac{3}{2}\cdot \ln |2x-1|+c$$

Caso 3 Funzioni razionali avente come numeratore una costante e come denominatore un quadrato Ricordiamo innanzitutto che:

$$\frac{1}{[f(x){]}^2}=[f(x){]}^{-2}\text{ e che }\int f^{\prime }(x)[f(x){]}^{n}dx=\frac{[f(x){]}^{n+1}}{n+1}$$

Esempio 4

$$\int \frac{5}{(2x-1{)}^2}dx=5\int (2x-1{)}^{-2}dx=\frac{5}{2}\int 2(2x-1{)}^{-2}dx=\frac{5}{2}\cdot \frac{(2x-1{)}^{-1}}{-1}+c$$

In generale Per prima cosa dobbiamo trovarci in una situazione dove al denominatore abbiamo un polinomio di grado maggiore del polinomio al numeratore, a questo punto possiamo individuare 3 casi:

• A

$$\int \frac{N(x)}{D(x)}dx\text{con }deg(N)=0,deg(D)=1$$

Qui abbiamo la funzione integranda con primitiva logaritmica

• B

$$\int \frac{A}{B{x}^2+Cx+D}dx$$

Oppure

$$\int \frac{Ax+E}{B{x}^2+Cx+D}dx$$

In entrambi i casi con $C^2-4BD<0$, ovvero il discriminante $\Delta <0$ associato al polinomio $D(x)$ al denominatore. Vedremo successivamente come risolverli

• C

Qui sono compresi tutti gli altri casi dove il grado del polinomio al numeratore è inferiore al grado del polinomio al denominatore, in questi casi si procede con il metodo di integrazione dei fratti semplici

Il metodo consiste nel riscrivere la funzione integranda come somma di funzioni razionali fratte i cui integrali sono noti, esiste un teorema sulla fattorizzazione dei polinomi che ci garantisce questi casi:

Esempio

$$\int \frac{1}{x^3-x^2}dx$$

CASO B Ritorniamo al calcolo di integrali con denominatore a delta negativo, per risolvere questi integrali dobbiamo distinguere due casi che si differenziano grazie al grado del polinomio al numeratore, utilizzeremo infatti due metodi diversi nei casi in cui il numeratore sia di grado 0 o di grado 1.

Caso 1, numeratore costante

Questo tipo di integrali si riconducono sempre ad un arcotangente. Per calcolare l’integrale dobbiamo scrivere il denominatore come somma tra una costante ed un quadrato perfetto in modo da ricondurci alla derivata di un arcotangente. Un metodo affidabile è quello di raccogliere a fattor comune il coefficiente $a$ del termine $a{x}^2$ per poi aggiungere e sottrarre $\frac{b^2}{4a^2}$

Esempio

Per questo tipo di integrali esiste una formula risolutiva che è la seguente:

$$\int \frac{k}{a{x}^2+bx+c}dx=\frac{2k\cdot \arctan (\frac{2ax+b}{\sqrt{-}\Delta })}{\sqrt{-}\Delta }+c_1,c_1\in \mathbb{R}$$

Esempio di prima con formula risolutiva:

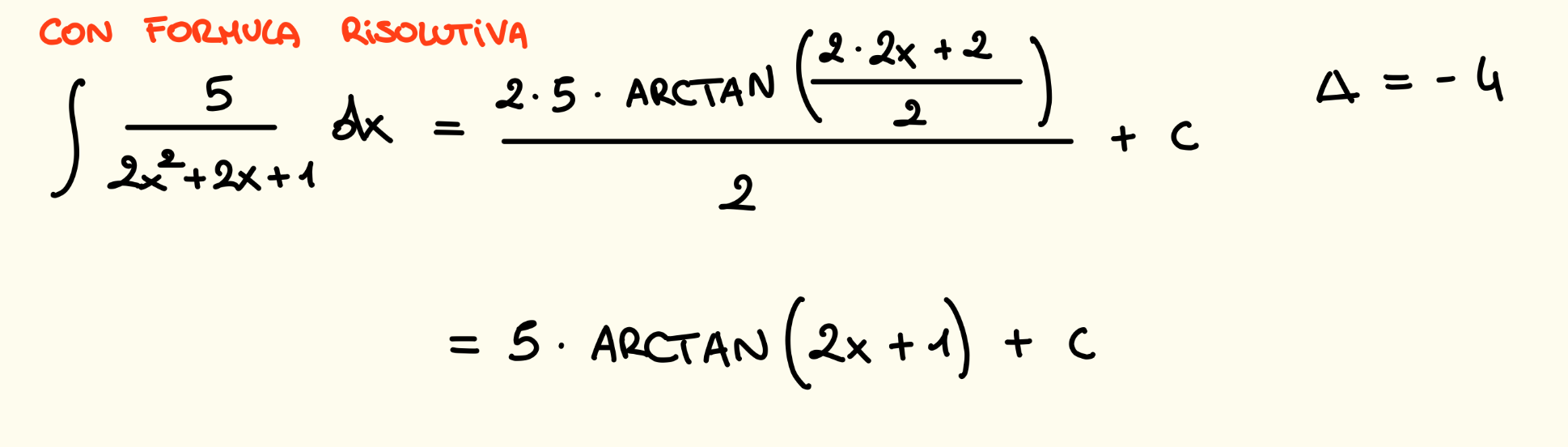
Caso 2 In questo caso abbiamo al numeratore un polinomio di primo grado. Questi integrali si riconducono sempre alla somma tra un logaritmo ed un arcotangente, dovremmo fare in modo di ottenere al numeratore la derivata prima del denominatore per poi spezzare l’integrale nella somma dei due integrali notevoli.

Quindi il primo sarà nella forma:

$$\int \frac{f^{\prime }(x)}{f(x)}dx=\log |f(x)|+c$$

Mentre il secondo:

$$\int \frac{k}{a{x}^2+bx+c}dx$$

Che sappiamo già come risolvere

Esempio

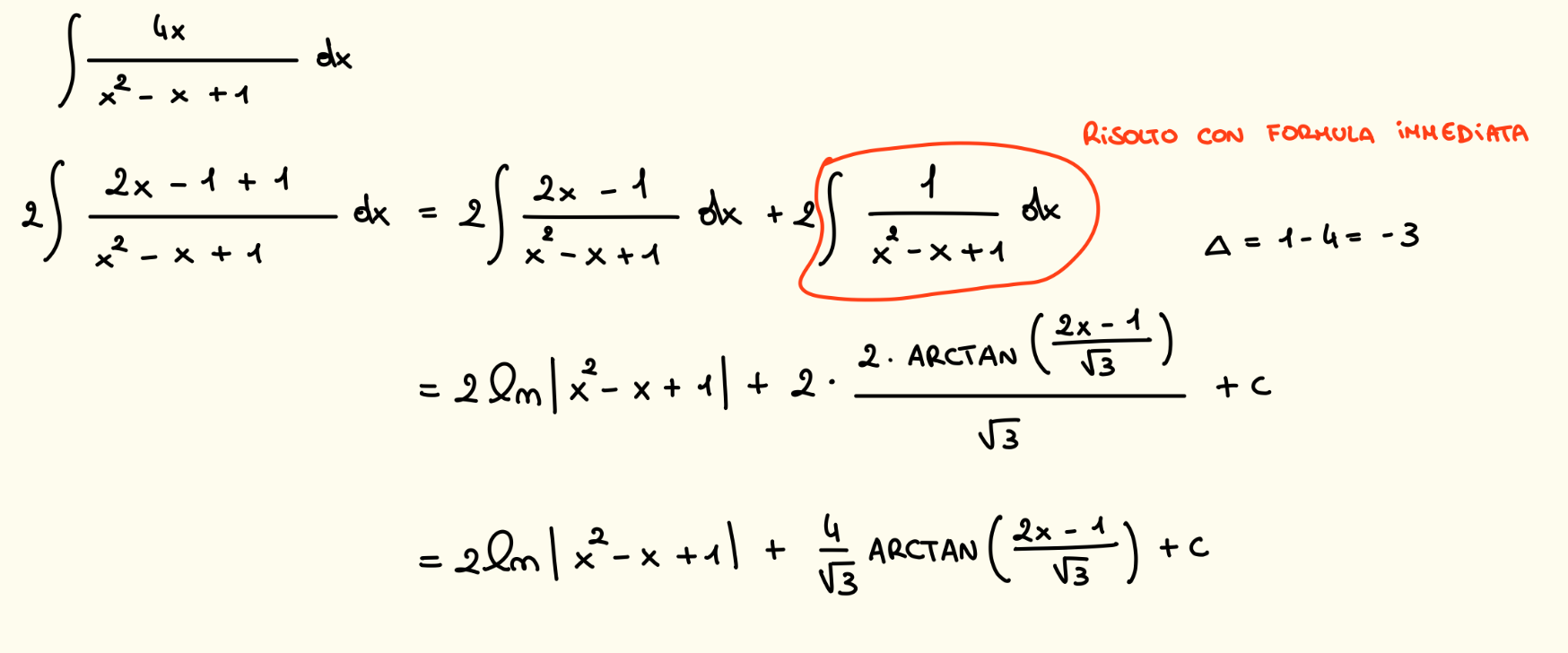
Integrali Impropri

Fino ad adesso abbiamo visto gli integrali di Riemann del tipo $f\in C^0([a,b])$

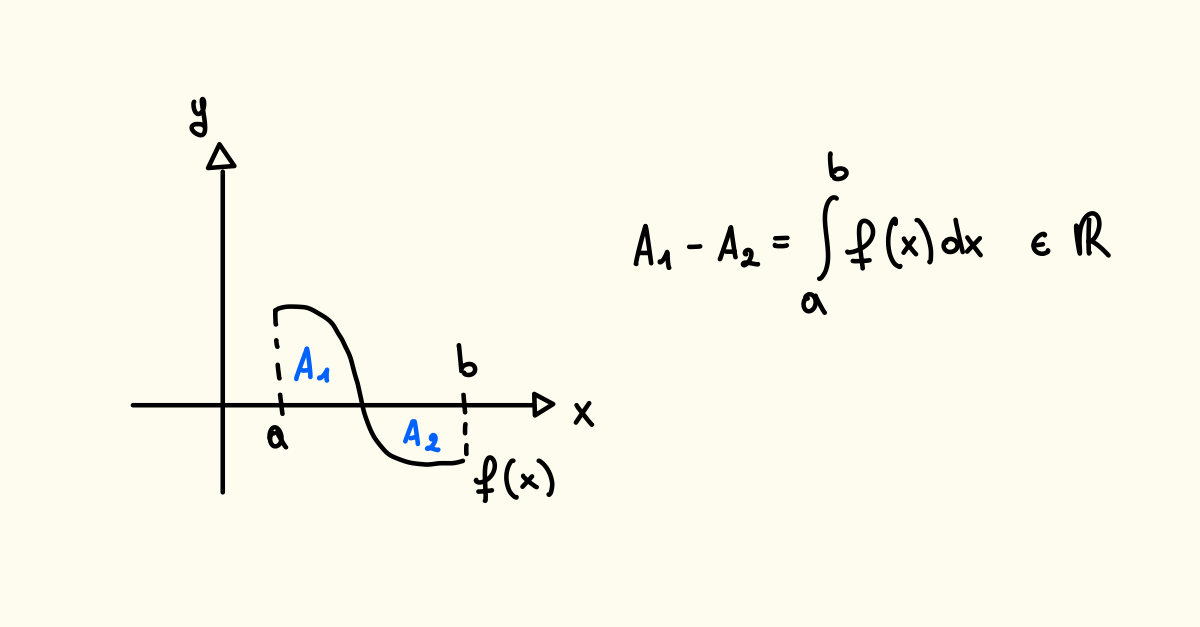
Ma cosa succede in questo caso?

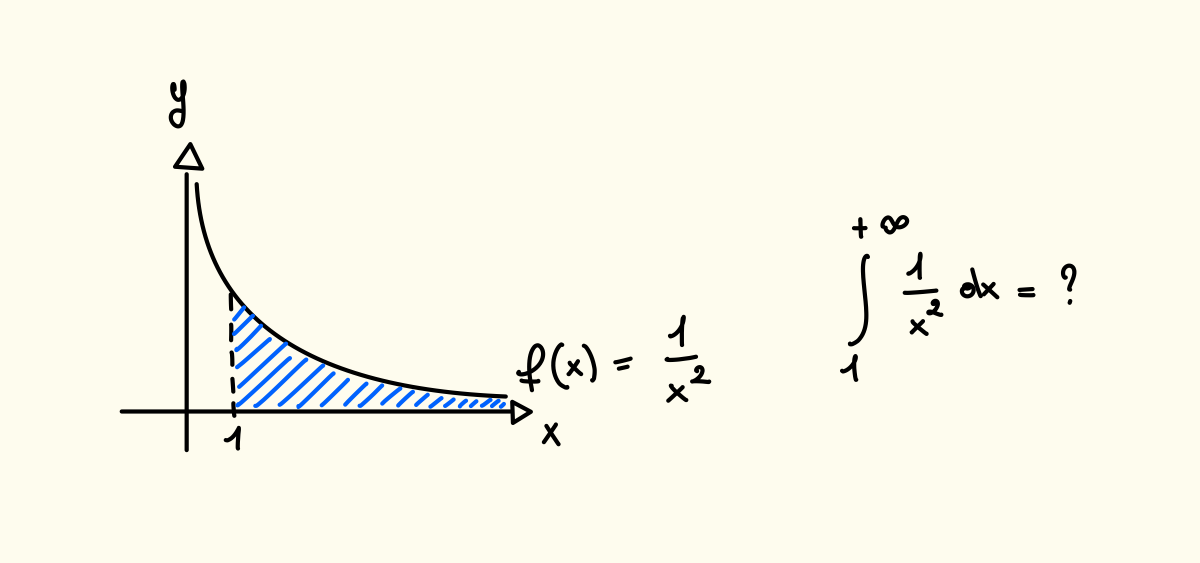
In questo caso l’integrale si definisce nel seguente modo:

Data $f\in C^0([a,b])$

$${\int }_a^{+\infty }f(x)dx=\underset{b\to +\infty }{\lim }{\int }_a^{b}f(x)dx$$

Se esiste il limite, questo è chiamato Integrale Improprio

Quindi:

$${\int }_a^{+\infty }f(x)dx=\underset{b\to +\infty }{\lim }(F(b)-F(a))$$

Esempi:

$$\begin{array}{rl}& {\int }_1^{+\infty }\frac{1}{x^2}dx=\underset{b\to +\infty }{\lim }{\int }_1^b\frac{1}{x^2}dx=\underset{b\to +\infty }{\lim }{\left[-\frac{1}{x}\right]}_1^b=\underset{b\to +\infty }{\lim }-\frac{1}{b}+1=1\\ & \\ & \text{—}\\ & \\ & {\int }_1^{+\infty }\frac{1}{x}dx=\underset{b\to +\infty }{\lim }[\ln |x|{]}_1^b=\underset{b\to +\infty }{\lim }\ln |b|-\ln |1|=+\infty \end{array}$$

Possiamo fare le seguenti osservazioni

$${\int }_1^b\frac{1}{x^{\alpha }}dx<+\infty <=>\alpha >1$$ $${\int }_1^b\frac{1}{x^{\alpha }}dx=+\infty <=>\alpha \le 1$$

Infatti possiamo notare un’analogia con la serie armonica generalizzata.

Esiste anche un altro tipo di integrali impropri, ovvero quando accade una situazione simile:

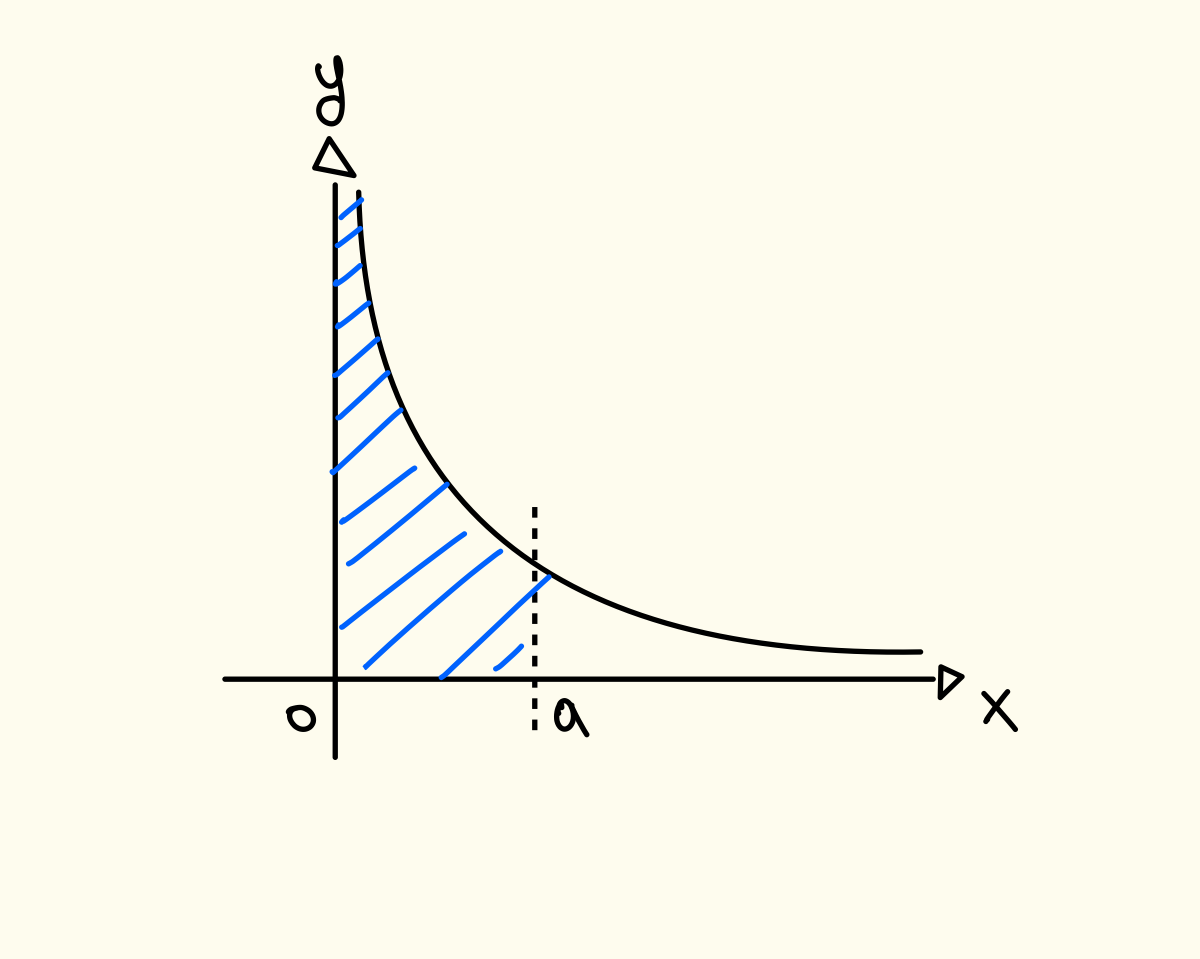
Anche in questo caso il metodo risolutivo è molto semplice ci basta infatti calcolare il limite per $a\to 0$ invece che per $b\to +\infty$.

Esempio

$${\int }_0^2\frac{1}{x}dx=\underset{a\to 0}{\lim }{\int }_a^2\frac{1}{x}dx=\underset{a\to 0}{\lim }[\ln |x|{]}_a^2=\underset{a\to 0}{\lim }(\ln |2|-\ln |a|)=+\infty$$

Non tutti gli integrali impropri sono ben definiti

Infatti in alcuni casi possiamo ottenere dei risultati non stabili ma che dipendono a quando ci fermiamo nell’integrazione, non lavorando quindi con un integrale improprio. Possiamo prendere come esempio

$${\int }_0^{+\infty }\cos (x)dx$$

Calcolandolo infatti andremo ad ottenere $\underset{b\to +\infty }{\lim }\sin (b)$ che non è ben definito

Caso Particolare

$${\int }_{-1}^1\frac{1}{x}dx$$

Anche in questo caso svolgendo i calcoli otteniamo un integrale non ben definito, osserviamo infatti anche il grafico:

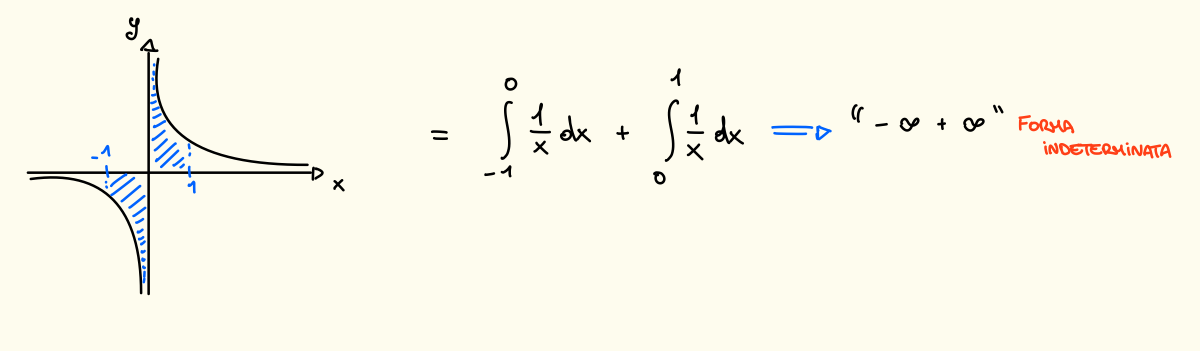
Possiamo però provare a formalizzare questa forma indeterminata dato che la funzione si comporta allo stesso modo, per fare questo possiamo ad esempio togliere alcuni valori dall’intervallo di integrazione:

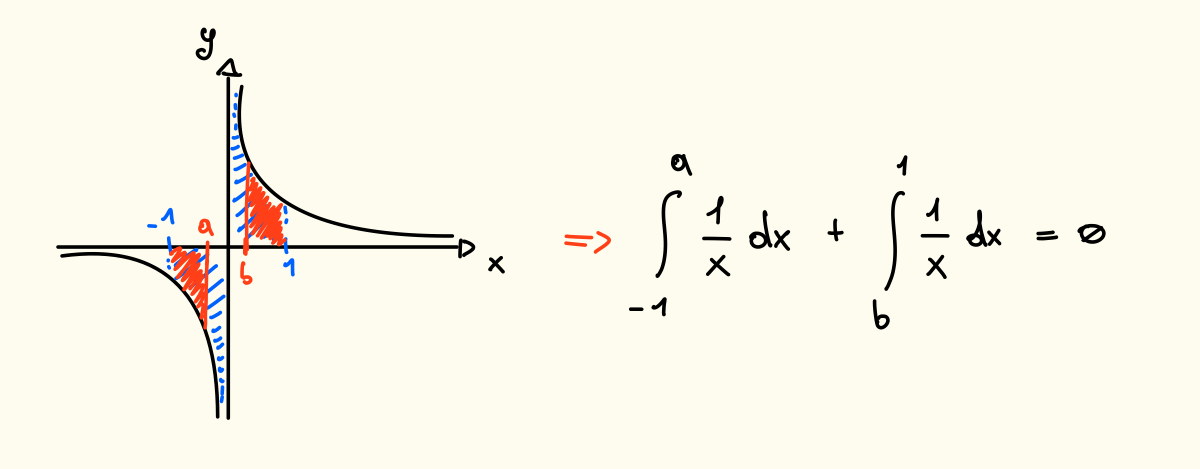
Questo integrale prende il nome di Valore Principale

Osservazione:

Devo sempre fare attenzione a prendere un intervallo simmetrico altrimenti potrei ottenere qualsiasi risultato, infatti:

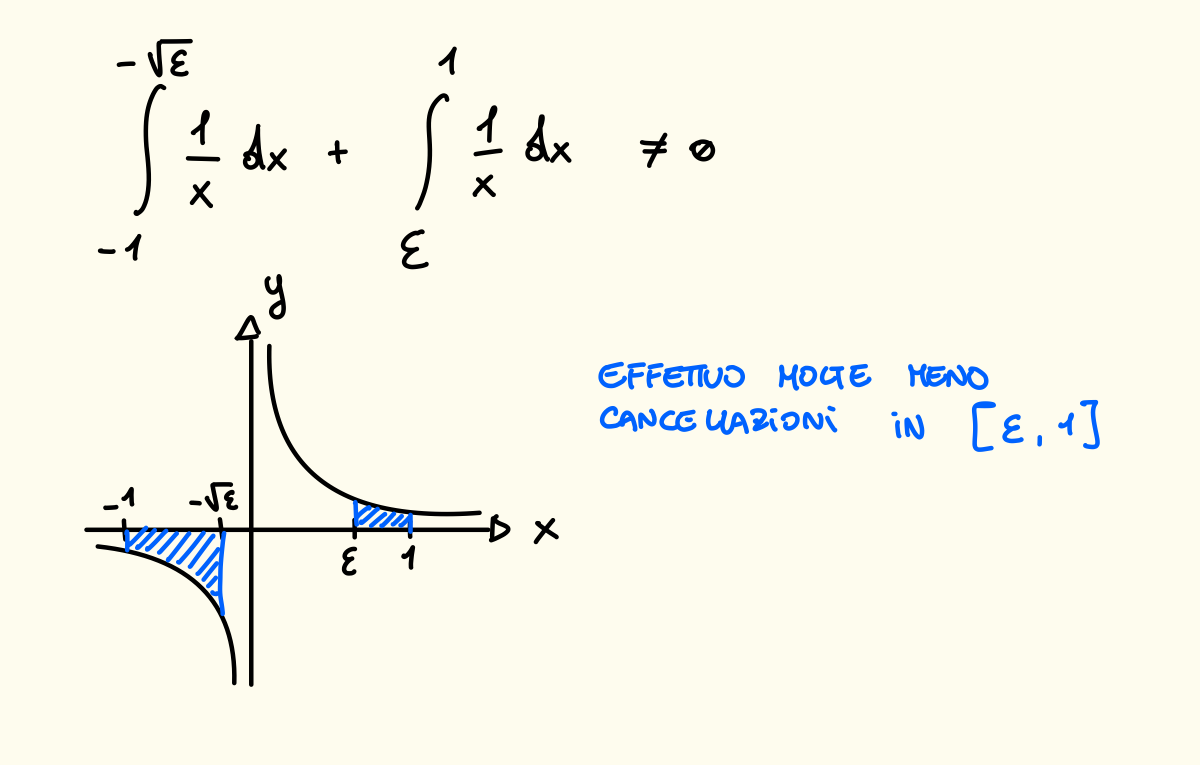
Riassunto Generale per gli Esercizi

• Derivate e Integrali Fondamentali

Per calcolare gli integrali cerchiamo una primitiva della funzione integranda, per gli integrali indefiniti aggiungiamo la costante $c$ per indicare tutta la famiglia delle primitive per gli integrali definiti la calcoliamo negli estremi $a,b$ nel modo: $F(a)-F(b)$ dove $F$ è la primitiva della funzione integranda.

Proprietà degli integrali

Linearità

$${\int }_a^{b}f(x)\pm g(x)dx={\int }_a^{b}f(x)dx\pm {\int }_a^{b}g(x)dx$$

Additività

$\forall a\le c\le b$

$${\int }_a^{b}f(x)dx={\int }_a^{c}f(x)dx+{\int }_c^{b}f(x)dx$$

Disuguaglianza Triangolare

$$\left|{\int }_a^{b}f(x)dx\right|\le {\int }_a^b\left|f(x)\right|dx$$

Costante Moltiplicativa

$$\int kf(x)dx=k\int f(x)dx$$

Integrali di Derivate di Funzioni Composte

Dato un integrale nella forma seguente possiamo risolverlo nel modo immediato:

$$\int f(g(x))\cdot g^{\prime }(x)dx=F(g(x))+c$$

Formule presenti sempre nella tabella.

Integrazione per Parti

Ricordare la formula:

$$\int f(x)g^{\prime }(x)dx=f(x)g(x)-\int f^{\prime }(x)g(x)dx$$

In alcuni casi è utile “aggiungere” 1 come fattore moltiplicativo per utilizzare l’integrazione parti. Può capitare che integrando per parti ritorniamo all’integrali di partenza con segno - davanti, in questo caso ci troviamo a risolvere un integrale ciclico, ci basta portarlo a sinistra dell’equazione e risolverlo.

Integrazione per Sostituzione

Utilizziamo la seguente formula:

$${\int }_a^{b}f(g(x))g^{\prime }(x)dx={\int }_{g(a)}^{g(b)}f(y)dy$$

Esempio

$$\begin{array}{rl}& \\ & \int \sin (e^{x)}{e}^{x}dx\\ & \text{Sostituzione: }y=e^x;dy=e^{x}dx\\ & \int \sin (y)dy=-\cos (y)+c=-\cos (e^x)+c\end{array}$$

Integrazione di Funzioni Razionali

Si tratta di integrare funzioni del tipo:

$$f(x)=\frac{P(x)}{Q(x)}\text{ con P(x) e Q(x) polinomi e Q(x)}\ne 0$$

• Nel caso in cui $P(x)$ sia la derivata di $Q(x)$ possiamo utilizzare la formula immediata:

$$\int \frac{f^{\prime }(x)}{f(x)}dx=\ln |f(x)|+c$$

• Casi nelle forme:

$$\int \frac{A}{B{x}^2+Cx+D}dx$$ $$\int \frac{Ax+E}{B{x}^2+Cx+D}dx$$

In entrambi questi casi deve verificarsi $\Delta <0$ del polinomio al denominatore.

Caso Numeratore Costante Nel primo caso dove abbiamo una costante al numeratore la soluzione si riconduce ad un arcotangente, dobbiamo riscrivere il denominatore come somma tra una costante ed un quadrato perfetto in modo da ricondurci alla derivata di un arcotangente. Per fare questo possiamo raccogliere a fattor comune il coeffieciente $a$ per poi aggiungere e sottrarre $\frac{b^2}{4a^2}$.

Oppure possiamo utilizzare la formula immediata:

$$\int \frac{k}{a{x}^2+bx+c}dx=\frac{2k\cdot \arctan (\frac{2ax+b}{\sqrt{-\Delta }})}{\sqrt{-\Delta }}+c_1$$

Caso Numeratore di Primo Grado In questo caso ci riconduciamo alla somma tra un logaritmo ed un arcotangente, dobbiamo ottenere al numeratore la derivata prima del denominatore per poi spezzare l’integrale nella somma dei due integrali notevoli.

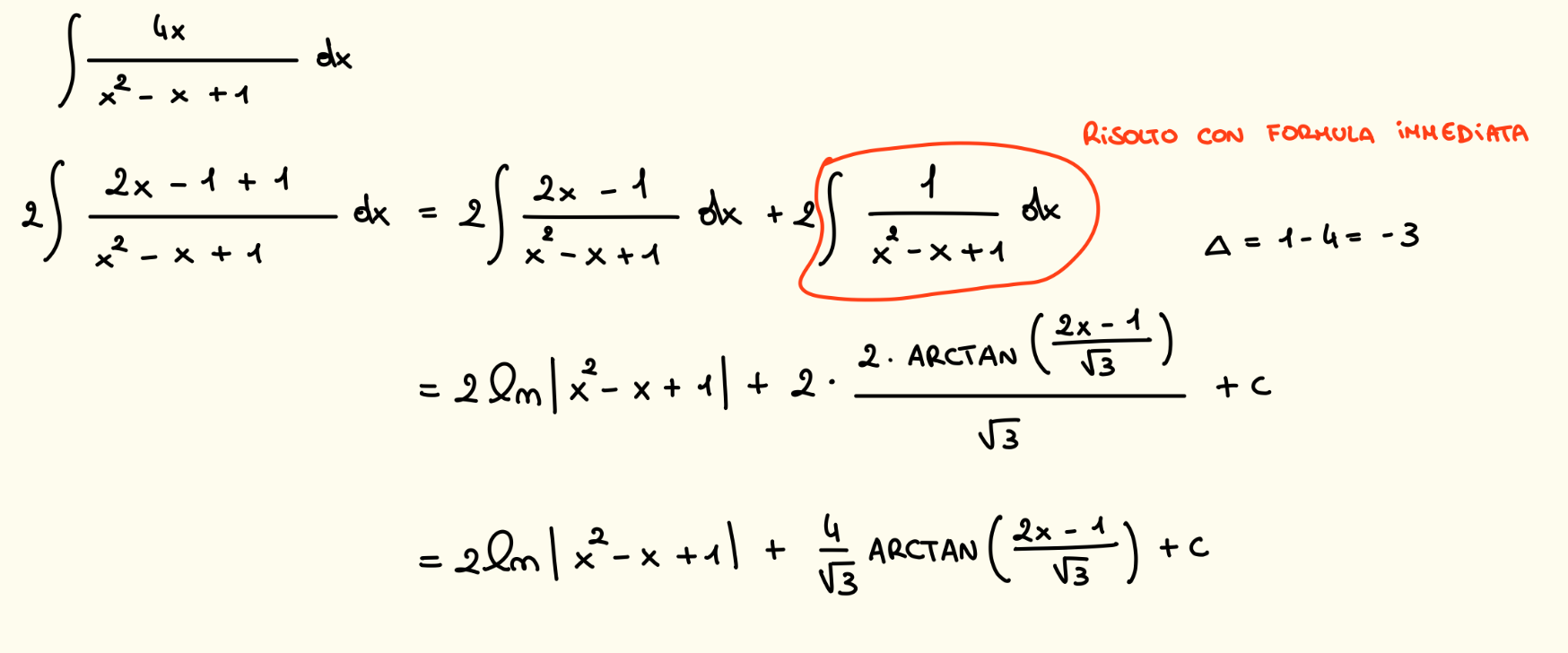
• In tutti gli altri casi dove il denominatore ha il grado maggiore del numeratore si procede con il metodo di integrazione dei fratti semplici, dobbiamo riscrivere la funzione integranda come somma di funzioni razionali di cui conosciamo gli integrali.

  Formule di scomposizione:

  

  Esempio:

  

Integrali Impropri

Sono integrali del tipo:

$${\int }_1^{+\infty }\frac{1}{x^2}dx$$

Quindi dove la funzione non è ben definita nell’intervallo.

Dobbiamo impostare il limite:

$$=\underset{b\to +\infty }{\lim }{\int }_1^b\frac{1}{x^2}dx=\underset{b\to +\infty }{\lim }{\left[-\frac{1}{x}\right]}_1^b=\underset{b\to +\infty }{\lim }\left(-\frac{1}{b}+1\right)=1$$

Osservazioni:

$${\int }_1^b\frac{1}{x^{\alpha }}dx<+\infty <=>\alpha >1$$ $${\int }_1^b\frac{1}{x^{\alpha }}dx=+\infty <=>\alpha \le 1$$

Si può verificare anche il caso:

$${\int }_0^2\frac{1}{x}dx$$

Anche in questo caso la funzione non è ben definita a 0 ma tende a $+\infty$. La risolviamo impostando il limite che tende a 0:

$${\int }_0^2\frac{1}{x}dx=\underset{a\to 0}{\lim }{\int }_a^2\frac{1}{x}dx=\underset{a\to 0}{\lim }[\ln |x|{]}_a^2=\underset{a\to 0}{\lim }(\ln |2|-\ln |a|)=+\infty$$

Non tutti gli integrali impropri sono ben definiti: Ad esempio il coseno da $0$ a $+\infty$ non si stabilizzerà mai come valore, possiamo anche provare algebricamente ma dovremmo calcolare il $\underset{b\to +\infty }{\lim }\sin (b)$ che appunto non è ben definito.

Caso Particolare:

$${\int }_{-1}^1\frac{1}{x}dx$$

In questo caso la funzione non è ben definita in 0 ma abbiamo un intervallo simmetrico rispetto all’origine e anche se calcolando gli integrali otteniamo una forma indeterminata $-\infty +\infty$ possiamo “formalizzarla” a 0 dato che le aree sono identiche.