Costo di un Algoritmo

Calcoleremo il costo degli algoritmi utilizzando il criterio della misura di costo uniforme. Il costo computazionale lo possiamo vedere come una funzione monotona non decrescente che rappresenta il tempo di esecuzione in base alla dimensione dell’input. Come prima cosa dobbiamo quindi definire la dimensione del nostro input che può essere il numero di elementi di una lista da ordinare, i nodi di un albero o il numero di elementi da cercare.

Il costo computazionale è ritenuto valido solo asintoticamente, ovvero attraverso la notazione asintotica.

Pseudocodice

Per valutare il costo computazionale non si scrive il codice in un linguaggio specifico ma lo pseudocodice ovvero un linguaggio di programmazione informale:

• si usano i costrutti di base come for, while, if
• si può usare la nostra lingua naturale per specificare passaggi
• si possono omettere molti dettagli al fine di rappresentare soltanto la soluzione vera e propria

Regole per valutare la complessità di un algoritmo

• Le istruzioni elementari hanno costo $\theta (1)$ (aritmetiche, lettura, assegnazione, if, stampa)
• Le istruzioni iterative hanno un costo pari alla somma dei costi massimi di ciascuna delle iterazioni, da notare che viene valutata anche la condizione (es. while) e che questa viene valutata una volta in più rispetto al numero delle iterazioni, ovvero quando l’iterazione termina.

Dipendenza del costo dall’input

Un algoritmo potrebbe avere tempi di esecuzione diversi a seconda dell’input, in questo caso dobbiamo individuare prima di tutto i casi migliore e peggiore, capire quindi quale input è più vantaggioso e quale no. É molto importante, a prescindere dall’input, trovare il tempo di esecuzione del caso peggiore in termini di $\theta$ o se non possibile arrotondarlo a $\text{ohm}$ oppure $O$.

Esempio: Troviamo il massimo in una lista di n valori

m = A[0] #Costo 1
for i in range(A): #Costo Θ(lunghezzaA)
	if i > m: #Costo 1
		m = i #Costo 1
print("Il valore massimo è: " + m) #Costo 1

$T(n)=\theta (1)+n[\theta (1)+\theta (1)]+\theta (1)=\theta (n)$

All’interno dell’iterazione le operazione hanno tutte lo stesso costo quindi possiamo svolgere il prodotto

In realtà la complessità sarebbe $lunghezza-1$ ma le costanti non le consideriamo nel calcolo dei limiti asintotici.

Variazione dei tempi di esecuzione di un algoritmo in funzione del suo costo computazionale

Ipotizziamo di avere a disposizione una macchina in grado di svolgere un’operazione in un nanosecondo ($10^9$ operazioni al secondo) e supponiamo che la dimensione del problema sia $n=10^6$:

• Tempo di computazione $O(n)$ 1 millesimo di secondo
• Tempo di computazione $O(nlogn)$ 20 millesimi di secondo
• Tempo di computazione $O(n^2)$ 1000 secondi = 16 minuti

E se il costo cresce esponenzialmente $O(2^n)$? Anche se abbassassimo $n=100$ con la stessa macchina vista prima avremo un costo pari a $\frac{2^{100}}{10^9}=\frac{2^{{10}^{10}}}{10^{3^3}}=\frac{1024^{10}}{1000^3}=\frac{1000^{10}}{1000^3}=10^{21}\text{ secondi}$ ovvero circa $10^{10}$ secoli.

Un algoritmo con una complessità esponenziale non serve a molto

Anche con un avanzamento tecnologico un algoritmo del genere non è molto conveniente, ad esempio prendendo una macchina estremamente veloce in grado di risolvere un problema simile con $n=1000$ e prendendone un’altra 1000 volte più veloce, nello stesso periodo T riusciremo a risolvere soltanto un problema con $n=1010$, non abbiamo quindi fatto grandi progressi.

Algoritmi Ricorsivi

Una funzione si dice ricorsiva quando chiama se stessa.

• Deve avere un caso base
• E un meccanismo di calcolo ricorsivo, ovvero come posso calcolare il valore successivo conoscendo quello che ho

In ambito informatico di solito con la ricorsione risolviamo tanti piccoli sottoproblemi e combinando le soluzioni otteniamo la soluzione al problema originale.

Le chiamate a sottoproblemi devono sempre convergere ad un caso base per permettere la terminazione del programma

Ogni funzione, ricorsiva o non, richiede una certa quantità di memoria per:

• Caricare il codice
• Passare i parametri
• Memorizzare il valore delle variabili

In generale le funzioni ricorsive hanno maggiori esigenze in termini di memoria delle funzioni non ricorsive

Qualsiasi problema risolvibile con un algoritmo ricorsivo può essere risolto anche con un algoritmo iterativo Quando conviene quindi utilizzare un algoritmo ricorsivo?

• Quando permette di scrivere una soluzione in modo più chiaro e simile alla natura del problema
• Non conviene quando esiste una soluzione iterativa semplice e chiara
• Non conviene utilizzare la ricorsione quando è importante avere una buona efficienza

Abbiamo un costo elevato di spazio perchè ogni volta che andiamo in ricorsione creiamo una copia della lista con un elemento in meno, possiamo ottimizzare il codice passando un indice invece che delle copie della lista:

Costo di fibonacci iterativo e ricorsivo

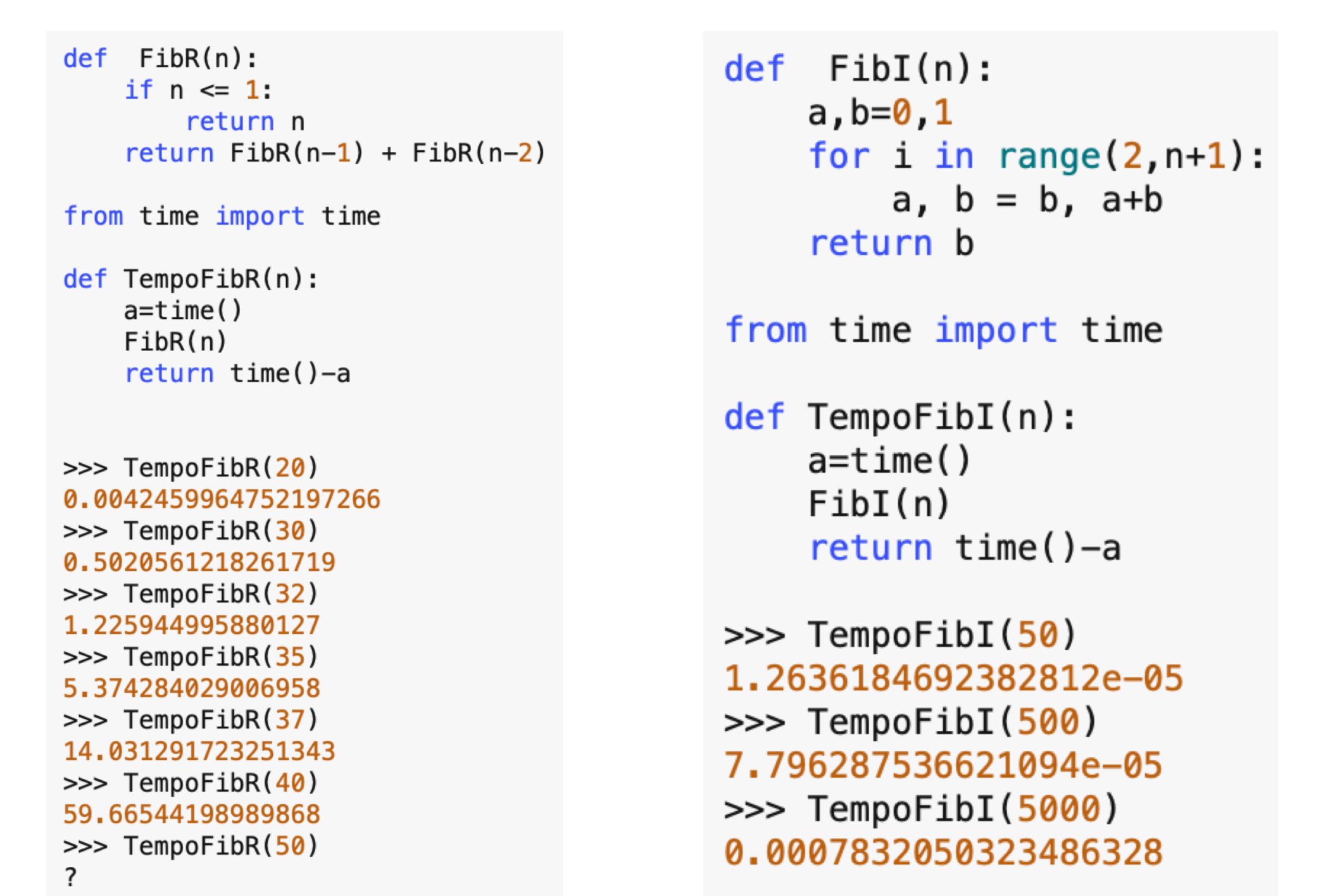
Il calcolo di Fibonacci ricorsivo ha costo in memoria molto elevato e vedremo più avanti un costo in tempo di $\theta (n^2)$ mentre la sua versione iterativi ha spazio $\theta (1)$ e in tempo $\theta (n)$ Questo perchè nella versione ricorsiva eseguiamo tantissimi calcoli che abbiamo già svolto precedentemente

Equazione di ricorrenza

Calcolare la complessità di un algoritmo ricorsivo è più complesso ad uno iterativo infatti questo da luogo ad una funzione di costo anch’essa ricorsiva. Trovarla è abbastanza semplice ma questa va riformulata in modo da non renderla ricorsiva altrimenti ci sarà impossibile quantificare il costo asintotico. Per riformulare la funzione di costo si imposta una equazione di ricorrenza costituita dalla formulazione ricorsiva e dal caso base.

L’equazione deve essere sempre costituita dalla somma di almeno due addendi, uno contiene la parte ricorsiva mentre l’altro il costo di tutto quello che avviene al di fuori della chiamata ricorsiva. DEVE ESSERE SEMPRE PRESENTE UN CASO BASE

Per risolvere le equazioni di ricorrenza abbiamo a disposizione 4 metodi:

• metodo iterativo
• metodo dell’albero
• metodo di sostituzione
• metodo principale

Metodo Iterativo

In questo metodo sviluppiamo l’equazione in modo da esprimerla come somma di termini dipendenti da $n$ e dal caso base. Contro: Maggiore quantità di calcoli algebrici rispetto agli altri metodi.

Esempi:

Calcolo di Fibonacci

Non siamo quindi riusciti a trovare la crescita asintotica precisa ma abbiamo comunque potuto approssimarla e notare che il calcolo di un numero di Fibonacci in modo ricorsivo ha costo esponenziale.

Metodo dell’albero

In questo metodo rappresentiamo graficamente lo sviluppo ricorsivo e vediamo il costo passo per passo.

Esempio: $T(n)=2T(\frac{n}{2})+\theta (n)$ e come caso base $T(1)=\theta (1)$

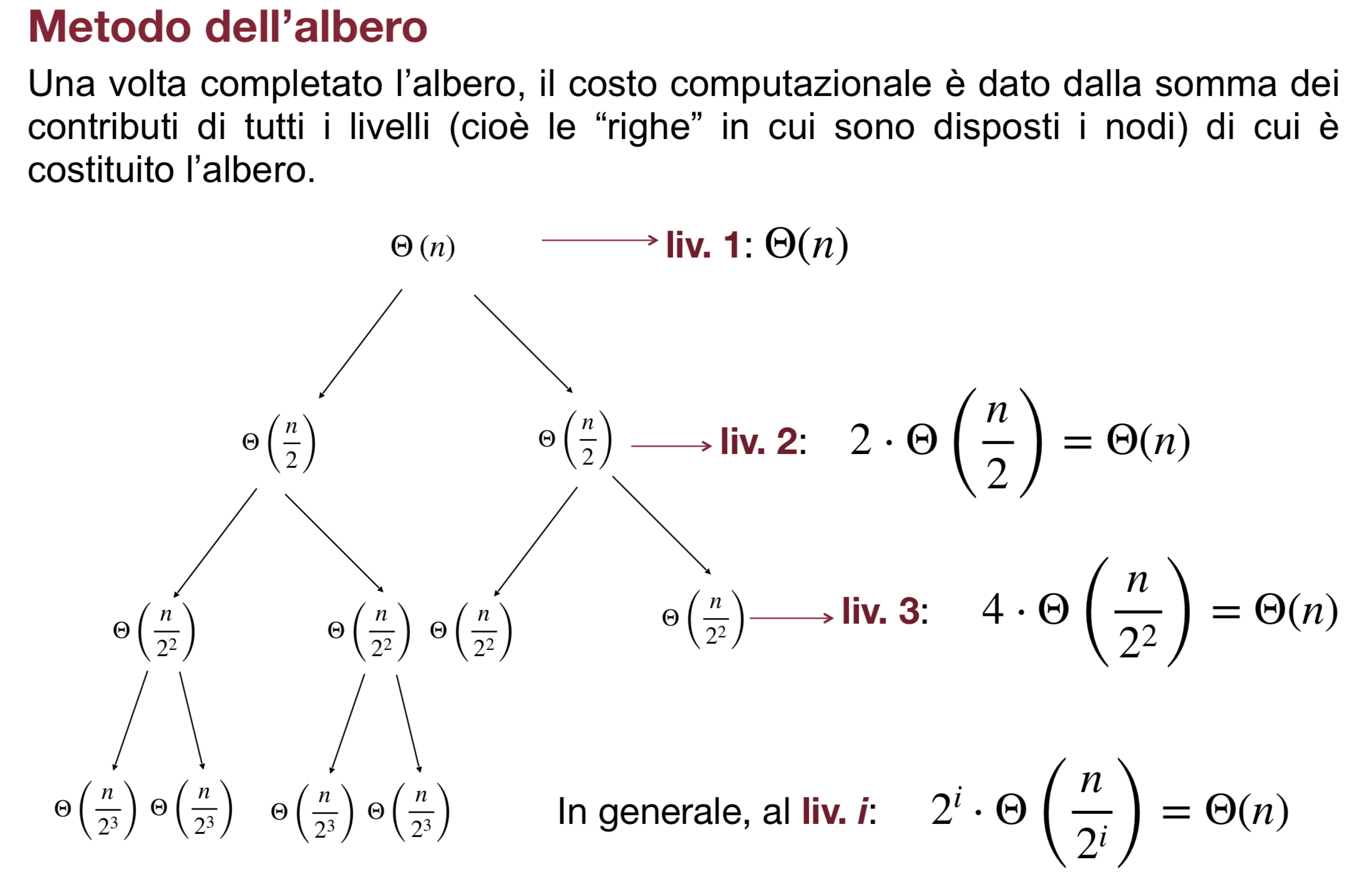
Quindi ogni nodo ha costo $\theta (n)$ e sommando tutti i valori che sono equivalenti a $logn$ otteniamo $\sum _{i=0}^{logn}\theta (n)=\theta (n)\sum _{i=0}^{logn}1=\theta (n)\ast logn=\theta (nlogn)$

Master Theorem

Questo metodo è molto meccanico ma non sempre applicabile, infatti possiamo utilizzarlo solo quando nella funzione di ricorrenza andiamo in ricorsione su un $n/x$.

Più nello specifico definiamo questa forma:

$T(n)=a\cdot T(\frac{n}{b})+f(n)$

• Se $f(n)$ = $O(n^{lo{g}_{b}a-ϵ})$ per qualche costante $ϵ>0$ allora $T(n)=\theta (n^{lo{b}_{b}a})$
• Se $f(n)=\theta (n^{lo{g}_{b}a})$ allora $T(n)=\theta (n^{lo{g}_{b}a}\cdot logn)$
• Se $f(n)=\text{ohm}(n^{lo{g}_{b}a+ϵ})$ per qualche costante $ϵ>0$ e se $a\cdot f(\frac{n}{b})\le c\cdot f(n)$ per qualche costante $c<1$ e per $n$ sufficientemente grande allora $T(n)=\theta (f(n))$.

Metodo di sostituzione

Con questo metodo non andiamo a trovare una soluzione ma ne dovremmo ipotizzare una e dimostrare che questa sia vera.

Esempio:

$$\begin{array}{rl}& T(n)=T(n-1)+\theta (1)\\ & T(1)=\theta (1)\end{array}$$

Per utilizzare questo metodo è necessario eliminare la notazione asintotica dall’equazione di ricorrenza, ottenendo quindi:

$$\begin{array}{rl}& T(n)=T(n-1)+b\\ & T(1)=a\end{array}$$

Per due costanti $a$ e $b$ fissate.

Ipotizziamo la soluzione $T(n)=O(n)$, ossia $T(n)\le c\cdot n$ dove $c$ è una costante che dobbiamo ancora determinare.

Caso Base: $T(1)=a\le c$ che sarà vera per $c\ge a$

Induzione Sostituendo nella formulazione ricorsiva otteniamo

$$T(n)\le c(n-1)+b=c\cdot n-c+b\le c\cdot n$$

Ottenendo quindi che la disequazione è vera quando $c\ge b$

Abbiamo quindi dimostrato che $T(n)$ è effettivamente un $O(n)$ poiché è possibile trovare un valore $c$ per il quale si ha $T(n)\le c\cdot n$ infatti basta prendere $c=max\{a,b\}$.

---

Troviamo adesso la notazione asintotica omega

Adesso dobbiamo ipotizzare una funzione che viene dominata da $T(n)$ quindi troviamo una costante $c$ tale che $T(n)\ge c\cdot n$

Come fatto prima sostituiamo nel caso base

$T(1)=a\ge c$ che viene soddisfatta quando $c\le a$

Sostituiamo nell’equazione di ricorrenza usando l’ipotesi induttiva

$$T(n)\ge c\cdot (n-1)+b=c\cdot n-c+b\ge c\cdot n$$

Che risulta vera nel caso in cui scegliamo $c\le b$

Abbiamo quindi dimostrato che $T(n)$ è un $\text{ohm}(n)$ dato che possiamo trovare un valore $c$ tale che $T(n)\ge c\cdot n$ ovvero basta prendere $c=min\{a,b\}$

---

Esempio più complesso

Sommatorie Notevoli