Automi

Forse provo a fare un PDF: automi.pdf

Introduzione alla Terminologia

Alcune definizioni:

• Alfabeto - Insieme finito di simboli, ad es $\Sigma =\{0,1,x,y,z\}$
• Stringa - Una sequenza di simboli che appartengono ad un alfabeto

Ad esempio dati $w_1,\dots ,w_n\in \Sigma$ abbiamo $w=w_1,\dots ,w_n$ come stringa dell’alfabeto.

• Linguaggio - Dato un alfabeto $\Sigma$ definiamo ${\Sigma }^{\ast }$ come linguaggio di $\Sigma$, ovvero l’insieme delle stringhe di quell’alfabeto.
• Lunghezza di una stringa - Data una stringa $w\in {\Sigma }^{\ast }$ definiamo $|w|$ come sua lunghezza ovvero quanti simboli contiene..
• Concatenazione - Data la stringa $x=x_1,\dots ,x_n\in {\Sigma }^{\ast }$ e la stringa $y=y_1,\dots ,y_m\in {\Sigma }^{\ast }$ definiamo come concatenazione di $x$ con $y$ la seguente stringa: $x_1,\dots x_n{y}_1,\dots ,y_m$
• Stringa vuota - Indichiamo con $ϵ$ la stringa vuota ovvero tale che:
  • $|ϵ|=0$
  • $\forall w\in {\Sigma }^{\ast }w\cdot ϵ=w$
  • ${\Sigma }^{\ast }\ne \varnothing \to w\in {\Sigma }^{\ast }$
• Conteggio - Data una stringa $w\in {\Sigma }^{\ast }$ e un simbolo $a\in \Sigma$ definiamo il conteggio di $a$ in $w$ come $|w{|}_a$ ovvero il numero di volte che compare il simbolo $a$ in $w$
• Stringa Rovesciata - Data una stringa $w=a_1\dots a_n\in {\Sigma }^{\ast }$, dove $a_1,\dots ,a_n\in \Sigma$, definiamo la stringa rovesciata con $w^R=a_n\dots a_1$
• Potenza - Data la stringa $w\in {\Sigma }^{\ast }$ e dato $n\in \mathbb{N}$ definiamo come potenza:

$$w^n=\{\begin{array}{l}ϵ\text{se }n=0\\ w{w}^{n-1}\text{se }n>0\end{array}$$

DFA

Il modello di computazione che useremo all’inizio è un automa a stati finiti, questo ha una memoria limitata e una gestione dell’input ma garantisce un’estrema semplicità.

Esempio - Un sensore per una porta automatica, questo ha solo 2 stati ovvero aperto e chiuso e a seconda dell’input del sensore cambia stato, se c’è qualcuno si apre altrimenti si chiude.

Definizione - DFA - Deterministic Finete Automaton

Un DFA è una tupla $(Q,\Sigma ,\delta ,q_0,F)$ dove:

• $Q$ è l’insieme finito degli stati
• $\Sigma$ è l’insieme finito dei simboli in input
• $\delta :Q\times \Sigma \to Q$ ovvero la funzione di transizione degli stati
• $q_0\in Q$ è lo stato iniziale
• $F\subseteq Q$ E’ l’insieme degli stati di accettazione dell’automa, ovvero gli stati dove l’automa si trova dopo aver letto una determinata stringa e consente la terminazione.

Se $M$ è un DFA allora l’insieme delle stringhe riconosciute da esso si denota con $L(M)$, in generale è il linguaggio conosciuto da $M$. Può anche accadere che $L(M)=\varnothing$.

Esempio - Il DFA precedente del sensore della porta avrà un linguaggio $w$ dove $w$ contiene almeno i 3 simboli:

• $N$ - nessuno si trova nei due lati della porta
• $A$ - qualcuno si trova nel lato anteriore
• $P$ - qualcuno si trova nel lato posteriore

Esercizio - Definire il linguaggio del seguente automa:

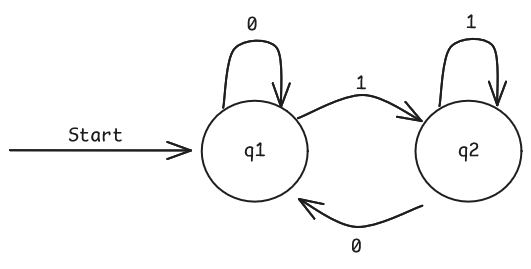
Per definire precisamente un linguaggio introduciamo la funzione di transizione estesa:

$${\delta }^{\ast }=Q\times {\Sigma }^{\ast }\to Q$$

Questa è definita in modo ricorsivo da:

$$\{\begin{array}{l}{\delta }^{\ast }(q,ϵ)=\delta (q,ϵ)=q\\ {\delta }^{\ast }(q,aw)={\delta }^{\ast }(\delta (q,a),w)\text{ con }w\in {\Sigma }^{\ast }\text{, e}\in \Sigma \end{array}$$

Configurazione

Sia $D:=(Q,\Sigma ,\delta ,q_0,F)$ un DFA definiamo la coppia $(q,w)\in Q\times {\Sigma }^{\ast }$ come configurazione di D.

Dato $x\in {\Sigma }^{\ast }$, la configurazione iniziale è $(q_0,x)$.

Passo di Computazione

Parte da una configurazione ad un’altra rispettando la funzione di transizione $\delta$. Il passaggio avviene rispettando la relazione binaria:

$$(p,ax){⊢}_M(q,x)\iff \delta (p,a)=q$$

Dove $p,q\in Q,a\in \Sigma ,x\in {\Sigma }^{\ast }$

Quindi una transizione avviene soltanto se la funzione di transizione la permette.

Possiamo estendere questa relazione binaria con il simbolo ${⊢}_M^{\ast }$ considerando anche la chiusura riflessiva e transitiva quindi:

• $(q,x){⊢}_M^{\ast }(q,x)$
• $(q,aby){⊢}_M(p,by)$ e $(p,by){⊢}_M(r,y)\Rightarrow (q,aby){⊢}_M^{\ast }(r,y)$ Dove:
• $q,p,r\in Q,a,b\in \Sigma ,y\in {\Sigma }^{\ast }$

Linguaggio Accettato

Diciamo che $x\in {\Sigma }^{\ast }$ è accettato da $M=(Q,\Sigma ,\delta ,q_0,f)$ se ${\delta }^{\ast }(q_0,x)\in f$ oppure $(q_0,x){⊢}_M^{\ast }(q,ϵ)$ con $q\in f$

In altre parole quindi: $L(M)=\{x\in {\Sigma }^{\ast }:{\delta }^{\ast }(q_0,x)\in f\}$ ovvero le parole del linguaggio devono permetterci di arrivare ad uno stato di terminazione.

Linguaggi Regolari

Definizione

$$REG=\{L\subseteq {\Sigma }^{\ast }:\exists \text{ DFA M t.c. }L(M)=L\}$$

Ovvero è l’insieme dei linguaggi accettati da almeno un DFA

Uno dei nostri obiettivi, ad esempio, sarà quello di progettare dei DFA per dei linguaggi forniti.

Esempio - Abbiamo il linguaggio $L=\{x\in \{0,1{\}}^{\ast }\text{ t.c }x=1y,y\in \{0,1{\}}^{\ast }\}$

Un possibile DFA potrebbe essere:

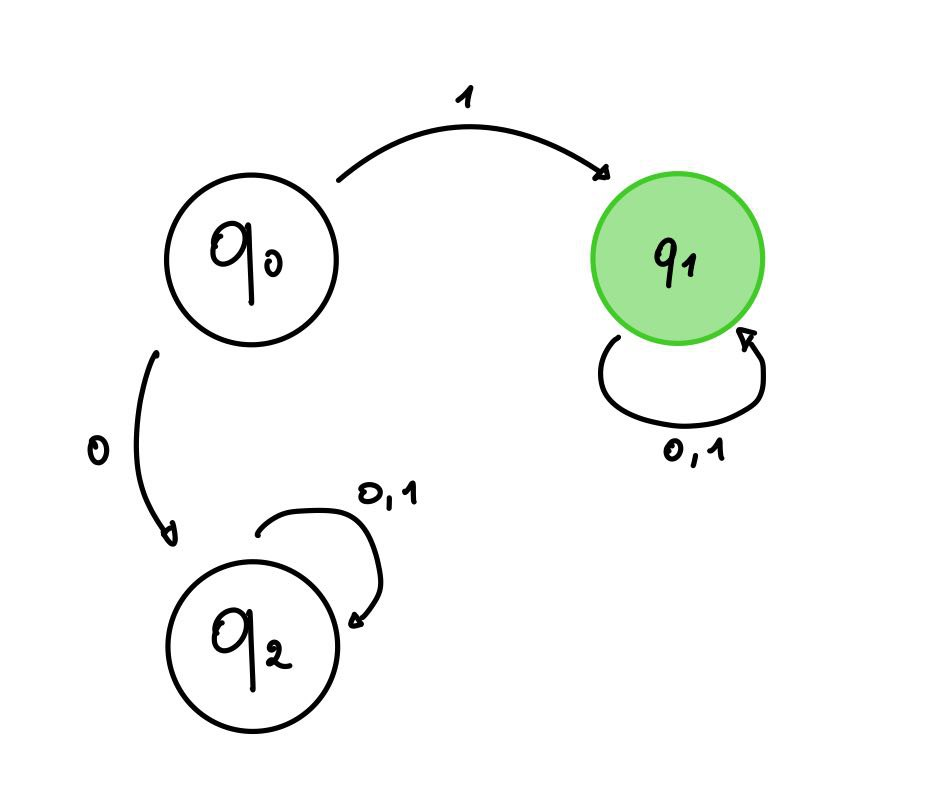
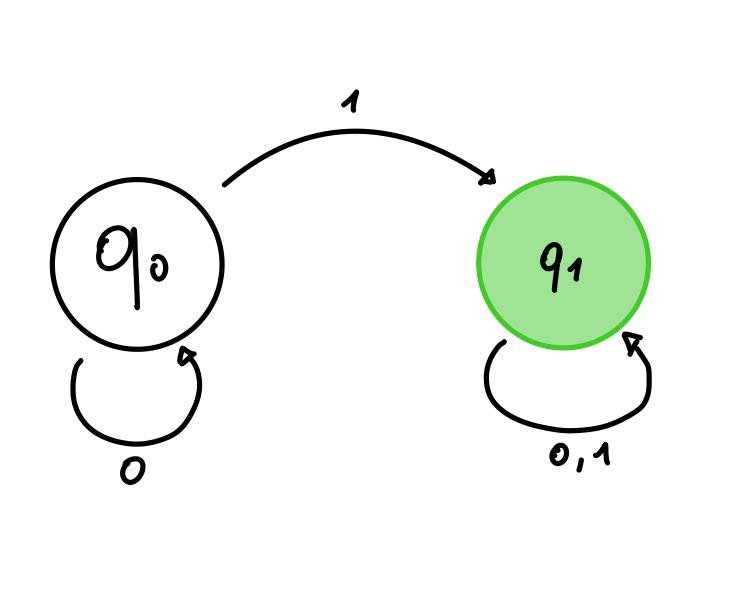
Notiamo quindi che questo accetta soltanto le stringhe che iniziano con il carattere ‘1’, infatti se riceve ‘1’ entra nello stato $q_1$ e non esce più, mentre se riceve ‘0’ entra nello stato $q_2$ senza più uscire.

Attenzione

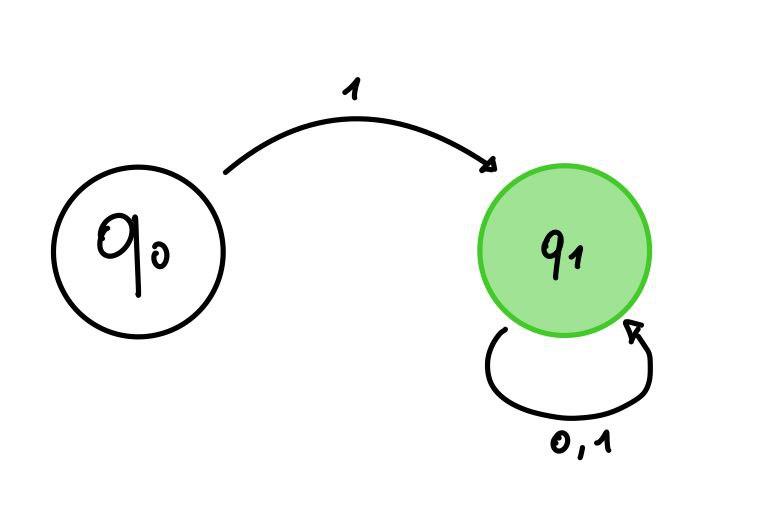
Lo stato $q_2$ dal quale non usciamo più, anche chiamato stato pozzo, è necessario infatti non possiamo toglierlo e inserire soltanto la transizione che da $q_0$ ricevendo ‘0’ rimaniamo in $q_0$ come in questo caso:

Progettando l’automa in questo modo infatti accetterà anche le stringhe che iniziano con ‘0’.

Una notazione che si usa se vogliamo non disegnare lo stato pozzo $q_2$ è quella di non indicare semplicemente la transizione, quindi:

Adesso dobbiamo dimostrare che questo DFA accetta il linguaggio, quindi più formalmente:

$$\text{DFA accetta }x\iff x\in L$$

Iniziamo osservando che se ci troviamo in $q_1$ rimarremo sempre in $q_1$ e stessa cosa anche per $q_2$, formalmente:

$$\begin{array}{r}{\delta }^{\ast }(q_1,u)=q_1\forall u\in \{0,1{\}}^{\ast }\\ {\delta }^{\ast }(q_2,u)=q_2\forall u\in \{0,1{\}}^{\ast }\end{array}$$

Tenendo in mente questo ragionamento iniziamo la dimostrazione per induzione.

• Case Base

$$\begin{array}{rl}& \text{Abbiamo }|x|=0\text{ quindi }x=ϵ\\ & \\ & {\delta }^{\ast }(q_0,ϵ)=\delta (q_0,ϵ)=q_0\notin f\end{array}$$

Quindi con una stringa vuota rimaniamo sempre in $q_0$ che non è uno stato di accettazione del DFA.

• Passo Induttivo

In questo caso abbiamo quindi $|w|\le n$ con $n>0$, e quindi la funzione di transizione estesa avrà questi risultati possibili:

$${\delta }^{\ast }(q_0,w)=\{\begin{array}{l}{q}_0\text{ se }w=ϵ\\ q_1\text{ se }w\text{ inizia con 1}\\ q_2\text{ se }w\text{ inizia con 0}\end{array}$$

Adesso prendiamo una stringa $|x|=n+1$ e la pensiamo costruita come $x=au$ con $a\in \{0,1\}$ e $u\in \{0,1{\}}^{\ast }$, la funzione di transizione ci restituirà:

$${\delta }^{\ast }(q_0,x)={\delta }^{\ast }(q_0,au)={\delta }^{\ast }(\underset{\text{solo 2 soluzioni}}{\underbrace{\delta (q_0,a)}},u)$$

Le due soluzioni di quel passaggio sono:

• $\delta (q_0,a)=q_1$ se $a=1$
• $\delta (q_0,a)=q_2$ se $a=0$

Ma poi, ricordando cosa abbiamo detto all’inizio, sappiamo che sia che ci troviamo in $q_1$ o $q_2$ rimarremo sempre li, indipendentemente da come è fatta la stringa $u$.

Operazioni sui Linguaggi

Unione

$$L_1\cup L_2=\{x\in {\Sigma }^{\ast }:x\in L_1\vee x\in L_2\}$$

Intersezione

$$L_1\cap L_2=\{x\in {\Sigma }^{\ast }:x\in L_1\wedge x\in L_2\}$$

Complemento

$$\overline{L}=\{x\in {\Sigma }^{\ast }:x\notin L\}$$

Concatenazione

$$L_1\circ L_2=\{xy:x\in L_1\wedge y\in L_2\}$$

Da notare che non è commutativo, quindi:

$$L_1\circ L_2\ne L_2\circ L_1$$

Potenza

Possiamo definirla ricorsivamente:

$$\{\begin{array}{l}{L}^0=ϵ\\ L^{n+1}=L^n\circ L\end{array}$$

Operatore “star” *

$$L^{\ast }=\bigcup _{n\ge 0}{L}^n=\{ϵ\}\cup L^1\cup L^2\cup \dots$$

---

Adesso vogliamo studiare le proprietà di chiusura dei linguaggi naturali.

Ad esempio - Se $L_1,L_2\in REG$ possiamo dire che anche $L_1\cup L_2\in REG$? E la loro intersezione? E il complemento? ecc…

Dimostriamo tutti questi casi.

• Teorema - Chiusura per unione

Una prima idea è che:

$$L_1,L_2\in REG\Rightarrow \exists M_1,M_2\in DFA\text{ t.c. }L(M_1)=L_1,L(M_2)=L_2$$

Dobbiamo quindi definire un altro DFA $M$ t.c. $L(M)=L_1\cup L_2$. Ma dato una $x$ candidata non possiamo provare a vedere prima se $M_1(x)$ la accetta e poi controllare se la accetta $M_2(x)$ perché altrimenti l’automa $M$ perderebbe i suoi stati.

Il controllo va fatto in parallelo su entrambi e una volta controllato ogni carattere di $x$ aggiorniamo lo stato di $M$ di conseguenza.