Programmazione Dinamica

Abbiamo visto che la tecnica Divide et Impera segue 3 passi:

Dividi il problema in sottoproblemi più semplici
Risolvi ricorsivamente i sottoproblemi
Combina le soluzioni dei sottoproblemi per formare la soluzione del problema originale

In alcuni casi può capitare che le soluzioni ai sottoproblemi siano uguali, in questi casi gli algoritmi basati su divide et impera svolgono del lavoro inutile.

Si può osservare questo fenomeno molto facilmente nel calcolo dei numeri di fibonacci tramite algoritmo ricorsivo.

def Fib(n):
	if n <= 1: return 1
	return Fib(n-1) + Fib(n-2)

Ad esempio per calcolare $f ib (5)$ ci servirà calcolarlo anche di:

4 - che ci porterà a calcolare 3 e 2, e poi 1 e 0
3 - che ci porta di nuovo a calcolare 2, 1 e 0

Si vede meglio graficamente qui:

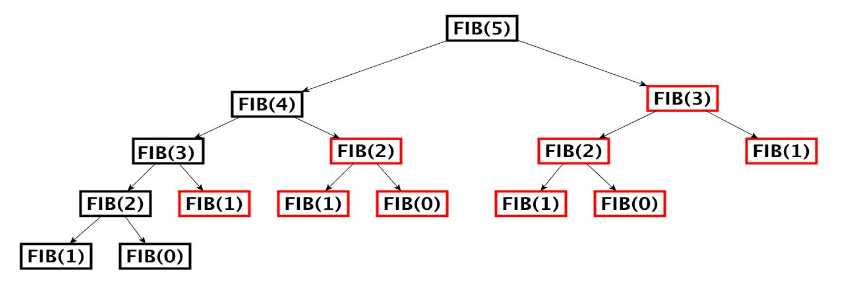
Una soluzione molto semplice è quella di salvare i valori già calcolati, questa tecnica prende il nome di memoizzazione. (non manca nessuna r :P).

Possiamo quindi memorizzare i valori e passare anche ad una versione iterativa:

def Fib2(n):
	F = [-1] * (n + 1)
	F[0] = F[1] = 1
	for i in range(2, n + 1):
		F[i] = F[i - 2] + F[i - 1]
	return F[n]

In questo modo otteniamo sempre un costo di tempo e spario pari a $Θ (n)$ ma un algoritmo iterativo che non occupa spazio sullo stack con altre chiamate.

Notiamo che possiamo eliminare la complessità di spazio memorizzando non tutta la lista ma soltanto gli ultimi due valori:

def Fib3(n):
	if n <= 1:
		return n
	a = b = 1
	for i in range(2, n + 1):
		a, b = b, a + b
	return b

Quindi:

Abbiamo provato una soluzione ricorsiva non efficiente perché c’era overlapping di sottoproblemi
Usando la memoizzazione ovvero salvando i risultati ottenuti in tabelle abbiamo risolto il problema del ricalcolo di sottoproblemi già esaminati
Siamo passati ad un algoritmo iterativo più efficiente e abbiamo migliorato anche il consumo di spazio mantenendo in memoria soltanto la parte di tabella che ci serviva per il seguito.

Da notare che nella versione ricorsiva si usa un approccio top-down infatti si parte dal problema principale e si scompone in problemi più piccoli fino ad arrivare a casi risolvibili.

Nell’algoritmo iterativo si usa un approccio bottom-up infatti si parte subito dai problemi più piccoli e si arriva pian piano a quelli più grandi

Esempio

Abbiamo $n$ file di varie dimensioni ciascuna inferiore a $C$ ed un disco di capacità $C$ .

Bisogna trovare il sottoinsieme di file che può essere memorizzato sul disco e che massimizza lo spazio occupato.

Progettare un algoritmo che, dati $C$ e la lista $A$ dove $A [i]$ è la dimensione del file i risolva il problema.

Ad esempio per $C = 100$ e $A = [82, 15, 40, 95, 31, 50, 40, 28]$ la risposta deve essere $2, 4, 7$ che occupa spazio $40 + 31 + 28 = 99$ .

Per questo problema non si conoscono algoritmi efficienti ma esistono algoritmi d’approssimazione efficiente con rapporti d’approssimazione costanti.

Iniziamo a fare delle osservazioni per costruire un algoritmo basato sul divide et impera:

Se la lista dei file risulta vuota o la capacità $C$ vale 0 allora la soluzione ottima vale 0
In caso contrario l’ultimo file della lista può appartenere o meno alla soluzione ottima
- Se l’ultimo file non appartiene alla soluzione allora i rimanenti $n - 1$ file devono essere una soluzione ottima per $(A [: - 1], C)$
- Se l’ultimo file appartiene alla soluzione allora i rimanenti $n - 1$ file devono essere una soluzione ottima per $(A [: - 1], C - A [n - 1])$
Possiamo ricondurci quindi al calcolo di due sottoproblemi di dimensione inferiore dato che non è presente l’ultimo file. Una volta risolti questi due sottoproblemi otteniamo i valori $v 1, v 2$ che ci fanno ottenere la soluzione del problema originale tramite: $ma x (v 1, v 2 + A [- 1])$

Possibile implementazione:

def es(A, i, C):
	if i == 0 or C == 0:
		return 0
	lascio = es(A, i - 1, C)
	if A[i - 1] > C:
		return lascio
	prendo = A[i - 1] + es(A, i - 1, C - A[i - 1])
	return max(lascio, prendo)

Questa ha una complessità di:

Ω (2^{\frac{n}{2}})

Anche qui il motivo di questi costi elevati è dato dall’overlapping dei sottoproblemi:

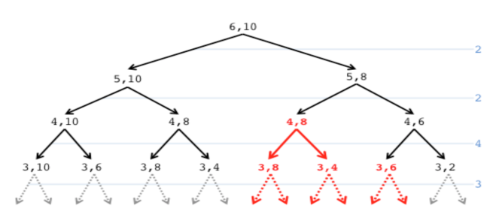
Ogni nodo è rappresentato dalla coppia (numero di file nell’istanza, capacità del disco). In rosso sono indicati i sottoproblemi che avevamo già calcolato in passato.

Più il problema iniziale è grande e più avremo overlapping.

Per evitare lavoro inutile ricorriamo alla memoizzazione utilizzando una tabella in cui salviamo i risultati calcolati e poterli riutilizzare più avanti.

Costruiamo una tabella $T$ di dimensioni $n \times (C + 1)$ e nella cella $T [i] [j]$ memorizzeremo il valore ottenuto dalla soluzione del sottoproblema in cui si hanno i soli primi $i$ file e la dimensione del disco è $j$ .

def es(A, C):
	T = [[-1] * (C + 1) for i in range(len(A) + 1)]
	return mem_es(A, len(A), C, T)
 
def mem_es(A, i, c, T):
	if T[i][c] == -1:
		if i == 0 or c == 0:
			T[i][c] = 0
		else:
			lascio = mem_es(A, i-1, c, T)
			T[i][c] = lascio
			if A[i-1] <= c:
				prendo = A[i-1] + mem_es(A, i-1, c-A[i-1], T)
				T[i][c] = max(lascio, prendo)
	return T[i][c]

La complessità di questa versione è dato da $O (n C)$ , abbiamo ottenuto un miglioramento? Si e no.

Se $C$ è molto grande alla la versione memoizzata è peggio di quella non ma se $C$ rimane piccolo allora questa versione è molto più efficiente.

Adesso eliminiamo la ricorsione nella versione memoizzata andando a modificare il calcolo della tabella.

Definiamo la tabella $T$ di dimensioni $(n + 1) \times (C + 1)$ dove:

$T [i, c]$ è lo spazio massimo con i primi $i$ file su un disco di capacità $c$ con $0 \leq i \leq n$ e $0 \leq c \leq C$
Troveremo quindi la soluzione al nostro problema nella cella $T [n] [C]$

Implementiamo un algoritmo che calcola la tabella:

def esI(A, C):
	n = len(A)
	T = [[0] * (C+1) for i in range(n+1)]
	for i in range(1, n+1):
		for c in range(C+1):
			if c < A[i-1]:
				T[i][c] = T[i-1][c]
			else:
				T[i][c] = max(T[i-1][c], A[i-1] + T[i-1][c-A[i-1]])
	return T[n][C]

In conclusione:

La programmazione dinamica può essere vista come il divide et impera, ovvero una tecnica che spezza il problema più grande in sottoproblemi ma grazie alla memoizzazione non ricalcola più volte lo stesso sottoproblema
Questi problemi possono essere risolti o con un approccio top down tipico degli algoritmi ricorsivi oppure bottom up, tipico invece di quelli iterativi.

Inoltre la tabella che riporta le soluzioni di tutti i sottoproblemi può essere usata anche per ripercorrere all’indietro le decisioni prese e ricavare la soluzione ottima.

Esempio

Abbiamo la tabella relativa a $C = 10, A = [1, 5, 3, 4, 2, 2]$

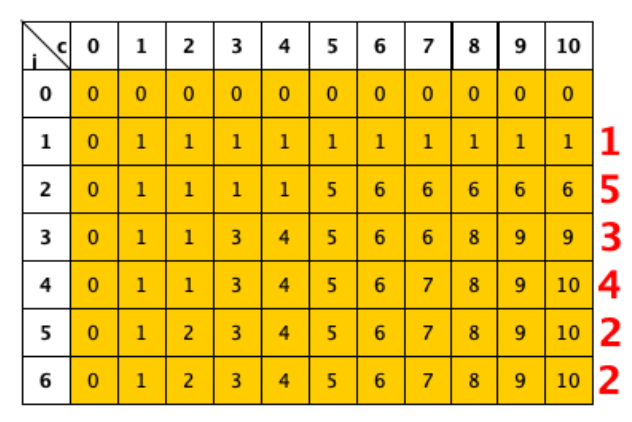
Adesso partendo da $T [n, C]$ tracciamo una freccia dagli elementi $T [k, c]$ verso gli elementi che ci hanno permesso di calcolare $T [k, c]$ e ci sono due opzioni:

$T [k - 1, c]$ e in questo caso abbiamo una freccia verticale e significa che il k-esimo file non è stato scelto
$T [k - 1, c - A [k]]$ e in questo caso abbiamo una freccia obliqua e significa che il file è stato scelto nella soluzione ottimale

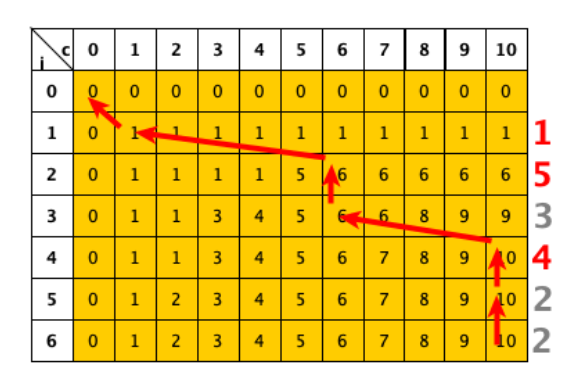
In questo caso quindi i file nella soluzione sono quelli di dimensione 1,5 e 4.

Implementazione:

def esI(A, C):
	n = len(A)
	T = [[0] * (C+1) for i in range(n+1)]
	for i in range(1, n+1):
		for c in range(C+1):
			if c < A[i-1]:
				T[i][c] = T[i-1][c]
			else:
					T[i][c] = max(T[i-1][c], A[i-1] + T[i-1][c-A[i-1]])
	valore = T[n][C]
	sol = []
	i = n
	while i > 0:
		if T[i][valore] != T[i-1][valore]:
			sol.append(i-1)
			valore -= A[i-1]
		i -= 1
	return T[n][C], sol

👨🏻‍💻 Alem's Notes

Programmazione Dinamica

Backlinks