Problemi di Ottimizzazione e Algoritmi di Ottimizzazione

In un problema di ottimizzazione abbiamo varie soluzione, ciascuna associata ad un valore che potrebbe essere ad esempio un costo o un beneficio.

A seconda del tipo di problema quindi potremmo voler massimizzare questo valore oppure minimizzarlo.

Il nostro obiettivo è quindi quello di scegliere la migliore soluzione fra quelle ammissibili ovvero quelle che soddisfano tutti i criteri del problema.

Esempio

Quando cerchiamo il percorso con costo minimo da a a b abbiamo come soluzioni ammissibili tutti i percorsi da a a b ma fra questi scegliamo soltanto quello con costo minimo ovvero la soluzione ottima.

---

Nella maggior parte dei casi, trovare una soluzione ottimale ad un problema di ottimizzazione richiede costo esponenziale rispetto alla dimensione del problema. In questo caso si parla di problema NP-Difficile.

Algoritmi di Approssimazione

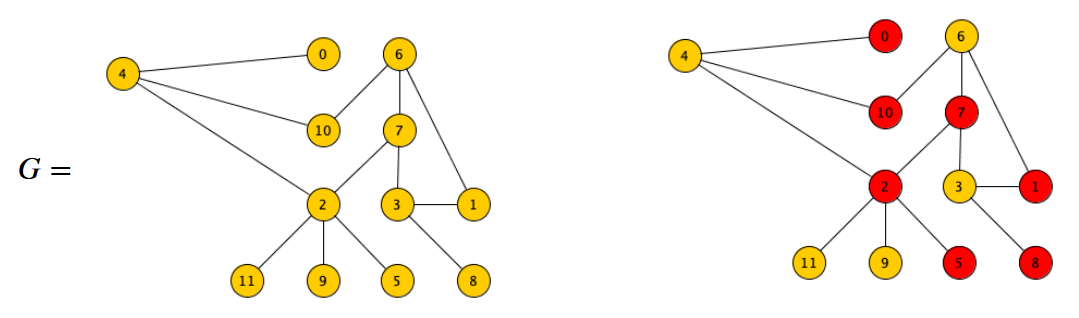
Prendiamo come esempio il problema di trovare una copertura tramite nodi di un grafo.

Dato un grafo non diretto G, una sua copertura tramite nodi è un sottoinsieme S dei suoi nodi tale che tutti gli archi di G hanno almeno un estremo in S.

Quindi, ad esempio:

Vogliamo trovare però la copertura tramite nodi di minima cardinalità, ovvero:

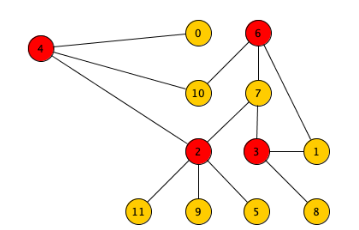
Una soluzione che utilizza la tecnica greedy potrebbe essere: Finché ci sono archi non coperti inserisci in S il nodo che copre il massimo numero di archi ancora da coprire.

Ma l’algoritmo non é corretto ad esempio in questo caso:

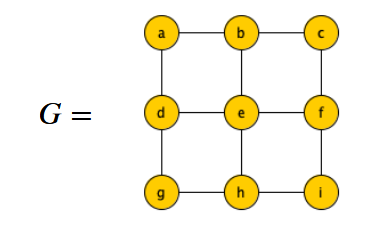
Infatti prenderebbe come primo nodo e e poi sarebbe costretto a sceglierne altri 4 da quelli più esterni, in tutto quindi 5 nodi.

In realtà però la soluzione ottimale ha solo 4 nodi, ovvero:

---

Spesso, come detto prima, non si hanno soluzioni efficienti per questi problemi ma soltanto esponenziali e quindi in questi casi ci si accontenta anche di una soluzione ammissibile che si avvicina ad una ottima, più è vicina e meglio è.

Fra questi algoritmi che non trovano sempre la soluzione ottima ma una ammissibile vicina dobbiamo fare una distinzione in:

• Algoritmi di Approssimazione - Questi sono algoritmi per i quali è stato dimostrato che la soluzione fornita avrà un certo grado di approssimazione rispetto alla soluzione ottima
• Euristiche - Per questi algoritmi invece non si riesce a dimostrare un grado di approssimazione però osservando vari esperimenti si nota che generalmente si comportano bene. Di solito vengono visti come “l’ultima spiaggia” quando non si trovano altri algoritmi più efficienti.

Per ora approfondiamo gli algoritmi di approssimazione, iniziando con i problemi di minimizzazione

Problemi di Minimizzazione

In questi problemi quindi cerchiamo la soluzione che ha il valore associato minore, quella con costo minimo.

Come si calcola questo grado di approssimazione rispetto alla soluzione ottima? Il modo usuale per misurarlo è il rapporto al caso pessimo tra il costo della soluzione prodotta e il costo della soluzione ottima.

Si dice che l’algoritmo $A$ approssima il problema di minimizzazione entro un fattore di approssimazione $\rho$ se per ogni istanza $I$ del problema vale:

$$\frac{A(I)}{OTT(I)}\le \rho$$

Dove:

• $OTT$ indica il costo della soluzione ottima per l’istanza $I$.
• $A(I)$ indica il costo della soluzione prodotta dall’algoritmo che stiamo testando per l’istanza $I$.

Rapporto nei problemi di massimizzazione

Per i problemi di massimizzazione invece vale il rapporto inverso:

$$\frac{OTT(I)}{A(I)}$$

Siccome si tratta di un problema di minimizzazione avremo sempre che $A(I)\ge OTT(I)$ e quindi il rapporto sarà sempre un numero maggiore o uguale a 1, nello specifico:

• Se $A$ approssima con fattore 1 allora è corretto perché trova sempre la soluzione ottima
• Se $A$ approssima entro fattore 2 allora trova sempre una soluzione con al più il doppio del costo della ottima
• Quindi più il rapporto è vicino a 1, più l’algoritmo è buono.

Ad esempio l’algoritmo trovato prima per la copertura avrebbe come fattore di approssimazione $\frac{5}{4}>1$ ma in altri casi potrebbe anche essere peggiore o migliore.

Questo algoritmo greedy quindi non garantisce nessun fattore di approssimazione costante.

---

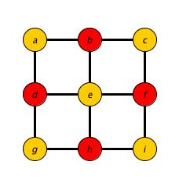
Dimostriamo che per ogni intero $l$ possiamo costruire un grafo $G_l$ su cui l’algoritmo greedy avrà rapporto di approssimazione $\Omega (\log l)$, il grafo $G_l$ è definito nel seguente modo:

• Diviso in $l$ livelli che vanno da 1 a $l$.
• Gli archi del grafo collegano nodi a livello $i>1$ con nodi a livello 1:
  • A livello $i$ sono presenti $\lfloor \frac{l}{i}\rfloor$ nodi e ciascuno di questi ha grado $i$. Ogni livello avrà in totale quindi $i\cdot \lfloor \frac{l}{i}\rfloor \le l$ archi che andranno a nodi distinti del livello 1.

Ad esempio, il grafo $G_5$ avrà la seguente struttura:

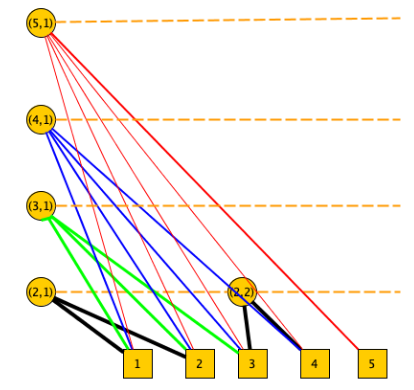
L’algoritmo in questo caso:

• Seleziona per primo il nodo a livello $l$ di grado $l$ dato che ha grado maggiore
• Poi seleziona uno dopo l’altro quelli di grado $l-1$
• …
• Continua fino a selezionare tutti i nodi di livello 2 di grado 2

Il costo della soluzione è:

$$\begin{array}{rl}c(SOL)& =\sum _{i=2}^l\lfloor \frac{l}{i}\rfloor \\ & \ge \sum _{i=2}^l\left(\frac{l}{i}-1\right)\\ & \ge l{\int }_2^{l+1}\frac{1}{x}dx-(l-1)\\ & =l\cdot {\log }_e(l+1)-l\cdot {\log }_{e}2-l+1\\ & \\ & \ge \Omega (l\cdot \log l)\end{array}$$

Da quanto ho capito si passa dalla sommatoria all’integrale per qualcosa di approssimazione 🤓

Notiamo che la soluzione ottima però è quella di selezionare i nodi a livello 1 dato che per costruzione tutti gli archi incidono su quei nodi, possiamo dire quindi che la soluzione ottima è quindi $O(l)$.

Con questi due dati otteniamo come rapporto:

$$\frac{\Omega (l\cdot \log l)}{O(l)}=\Omega (\log l)$$

---

L’aver dimostrato un fattore di approssimazione non costante per un algoritmo non significa che è uguale per tutti gli algoritmi rivolti a quel problema.

Consideriamo il seguente algoritmo greedy per trovare la copertura di nodi:

def copertura1(G):
	# Inizializza la lista degli archi E
	S = []
	while E != []:
		# Estrai da E un arco (x,y)
		if x not in S and y not in S:
			S.append(X)
			S.append(y)
	return S

Il rapporto d’approssimazione di questo algoritmo è 2.

Per questo problema non sono noti algoritmi d’approssimazione con rapporto inferiore a 2.

---

Dimostriamo il rapporto di approssimazione

Siano $e_1,e_2,\dots ,e_k$ gli archi di $G$ che vengono trovati non coperti durante l’esecuzione.

Per come funziona l’algoritmo, ovvero copre gli archi da entrambi gli estremi abbiamo che $A(I)=2k$. 2 nodi per ogni arco.

Questi archi saranno sicuramente disgiunti dato che per coprire un arco basta un solo nodo e se un arco non è coperto significa che nessuno dei due nodi è stato aggiunto.

Quindi per una soluzione ottimale ci serviranno sicuramente $k$ nodi e quindi $k\le OTT(I)$

Ricaviamo quindi che:

• $A(I)=2k\le 2\cdot OTT(I)$ da cui segue che $\frac{A(I)}{OTT(I)}\le 2$

---

Implementiamo l’algoritmo dove per rendere efficiente la ricerca di un nodo in S utilizziamo un vettore presi dove presi[i]=1 se il nodo $i$ è in S.

def copertura1(G):
	n = len(G)
	E = [(x,y) for x in range(n) for y in G[x] if x < y]
	presi = [0] * n
	Sol = []
	for a,b in E:
		if presi[a] == presi[b] == 0:
			Sol.append(a)
			Sol.append(b)
			presi[a] = presi[b] = 1
	return Sol

Che ha complessità di $O(n+m)$