Gli algoritmi Greedy

per presentare gli algoritmi greedy utilizziamo come esempio un problema più semplice chiamato selezione di attività

In questo problema abbiamo una lista di $n$ attività:

• Ogni attività è rappresentata da una coppia che indica il suo tempo di inizio e fine
• Due attività si dicono compatibili se la loro esecuzione non si sovrappone

Il nostro obiettivo è trovare un sottoinsieme di attività da eseguire che abbia la massima cardinalità.

Prendiamo il seguente insieme:

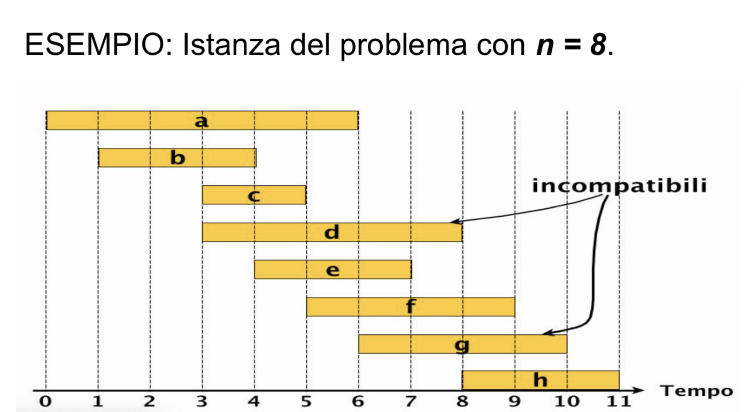
Qui possiamo vedere “a occhio” che l’insieme più grande è composto dalle 3 attività $b,e,h$.

Se volessimo usare un algoritmo greedy dovremmo trovare una regola che ci permetta di effettuare ogni volta la scelta giusta e non cambiare più questa scelta, alcune regole potrebbero essere:

• Prendere l’attività compatibile che inizia prima.
• Prendere l’attività compatibile che dura di meno.
• Prendere l’attività compatibile che ha meno conflitti con quelle ancora da prendere.

Spoiler Regole Giusta

La regola giusta da scegliere in questo caso è scegliere l’attività compatibile che finisce prima

Ci sarebbe la dimostrazione ma non credo la metto :P

• Implementazione:

def selezione_a(lista):
	lista.sort(key = lambda x: x[1])
	libero = 0
	sol = []
	for inizio, fine in lista:
		if libero < inizio:
			sol.append((inizio, fine))
			libero = fine
	return sol

Come complessità abbiamo:

• Ordinare la lista: $\Theta (n\log n)$
• Il for viene iterato $n$ volte e costa 1 quindi $\Theta (n)$
• In totale $\Theta (n\log n)$

---

Consideriamo il problema di assegnare le attività a delle aule e fare in modo di usare il minor numero di aule possibili, in un’aula ovviamente non possiamo eseguire più di una lezione contemporaneamente.

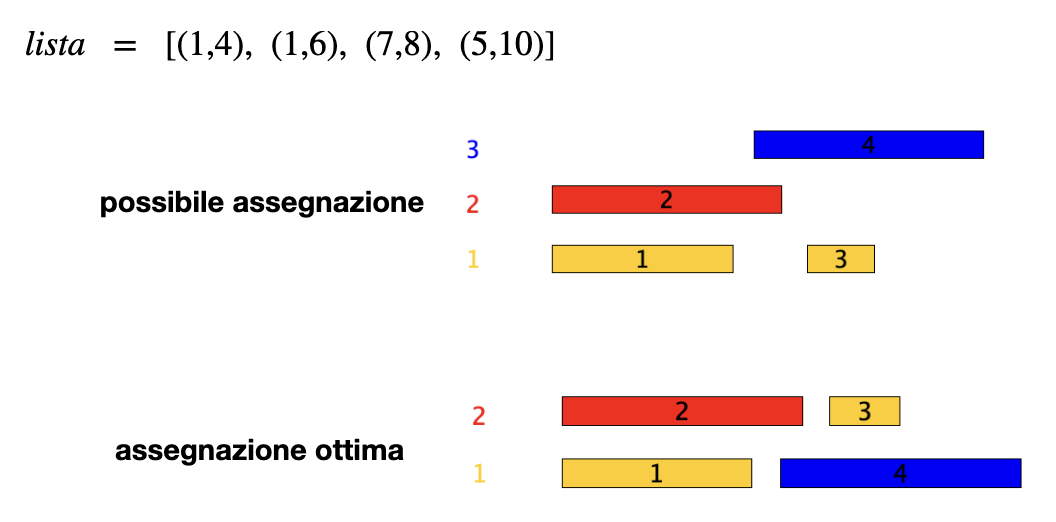
Un’idea per risolvere questo problema è:

• Inizializzare una lista di liste dove ogni lista corrisponde ad un’aula, iniziamo con una sola aula senza lezioni.
• Iteriamo finché la lista di attività non rimane vuota ed estraiamo da questa l’attività che inizia prima.
• Se nella soluzione c’è un’aula che può contenerla la assegnamo a quell’aula, altrimenti ne creiamo una nuova

Per contenere i costi utilizziamo una Heap:

def assegnazioneAule(lista):
	from heapq import heappop, heappush
	Sol = [[]]
	H = [(0,0)]
	lista.sort()
	for inizio, fine in lista:
		libera, aula = H[0]
		if libera < inizio:
			Sol[aula].append((inizio, fine))
			heappop(H)
			heappush(H, (fine, aula))
		else:
			Sol.append([(inizio, fine)])
			heappush(H, (fine, len(Sol)-1))
	return Sol

Come complessità abbiamo:

• Ordinare la lista: $\Theta (n\log n)$
• Eseguiamo il for $n$ volte e all’iterno del for al caso pessimo eseguiamo un’estrazione dall’heap e un inserimento nell’heap entrambe che costano $\Theta (\log n)$ quindi anche il for richiede $\Theta (n\log n)$
• In totale quindi $\Theta (n\log n)$