Backtracking

Raccolta di esercizi svolti con la tecnica backtracking, si basa sull’osservare l’albero che produciamo con il nostro algoritmo e “tagliare” i rami che non ci interessano per ridurre la complessità

Esercizio 1

Progettare un algoritmo che prende come parametro un intero $n$ e stampa tutte le stringhe binarie lunghe $n$.

Ad esempio per $n=3$ l’algoritmo deve stampare $2^3=8$ stringhe.

Notiamo che:

• Le stringhe da stampare sono $2^n$
• Per stampare una stringa lunga $n$ dobbiamo pagare $\Theta (n)$
• Quindi il meglio che possiamo ottenere da un algoritmo simile è $\Omega (2^n\cdot n)$

L’albero delle scelte possibili è il seguente:

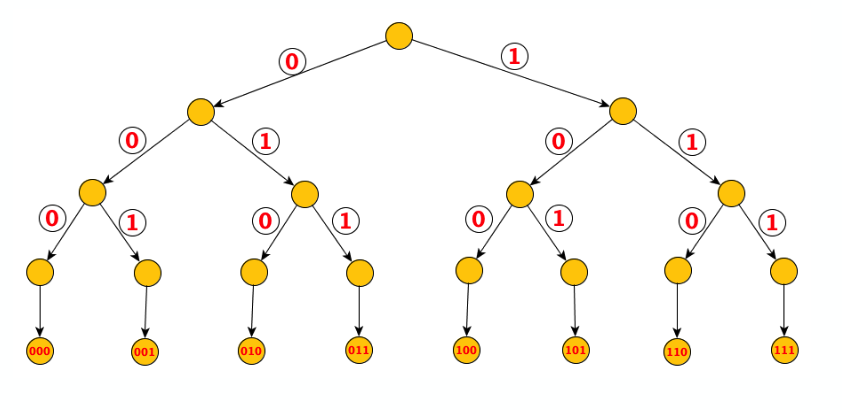
Scriviamo un algoritmo per risolvere il problema:

def bk(n, sol = None):
	if sol is None:
		sol = []
 
	if len(sol) == n:
		print(''.join(sol))
		return
 
	sol.append('0')
	bk(n, sol)
	sol.pop()
 
	sol.append('1')
	bk(n, sol)
	sol.pop()

Abbiamo ottenuto un algoritmo efficiente, infatti è uguale alla soglia minima descritta prima:

• L’albero ha $2^n-1$ nodi interni e $2^n$ foglie
• Ciascun nodo richiede $O(1)$
• Ciascuna foglia richiede $O(n)$ per essere stampata
• In totale abbiamo $O(2^n\cdot n)$

Esercizio 2

Progettare un algoritmo che prende come parametro due interi $n$ e $k$ con $0\le k\le n$ e stampa tutte le stringhe binarie lunghe $n$ che contengono al più $k$ 1.

Ad esempio per $n=4,k=2$ delle $2^4=16$ stringhe lunghe $n$ dobbiamo stampare soltanto le seguenti 11 strighe:

• 0000, 0001, 0010, 0100, 1000, 0011, 0101, 1001, 0110, 1010, 1100

Analizziamo l’albero delle scelte possibili e vediamo quali rami tagliare se $n=4$ e $k=1$:

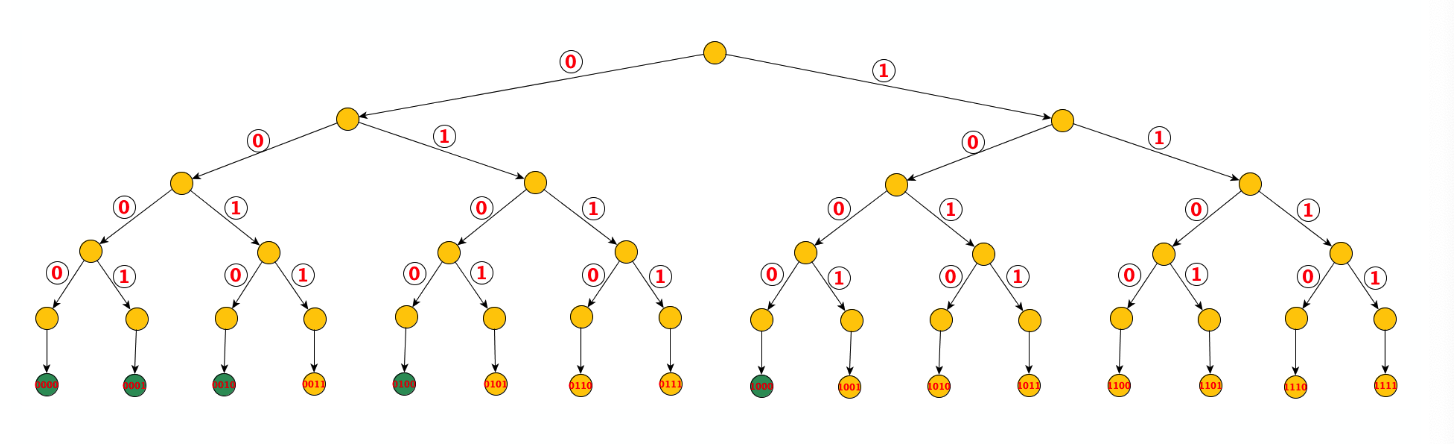
In verde sono indicate le foglie che vanno stampate

In generale possiamo non percorrere i seguenti percorsi:

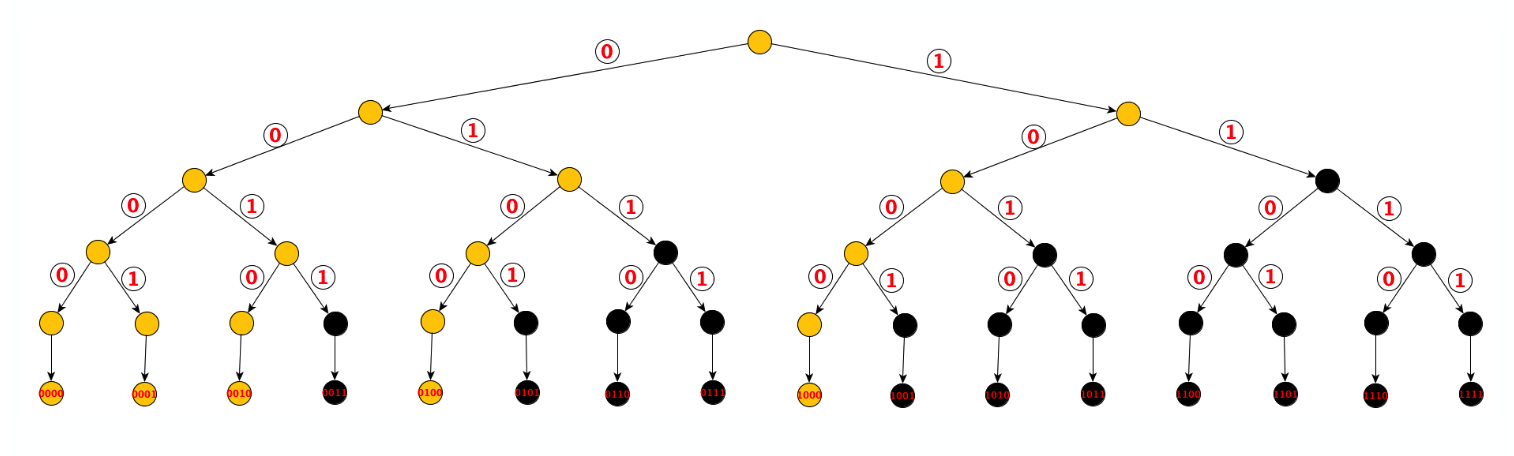
Analizziamo il tetto minimo per la complessità di un algoritmo che risolve il problema, in generale un buon algoritmo dovrebbe avere una complessità proporzionale al numero delle stringhe da stampare quindi $O(S(n,k)\cdot n)$, dove con $S(n,k)$ indichiamo il numero di stringhe da stampare.

Nel caso di $k=2$ si ha che:

$$S(n,k)=1+n+\left(\genfrac{}{}{0ex}{}{n}{2}\right)=\Theta (n^2)$$

• $\left(\genfrac{}{}{0ex}{}{n}{2}\right)$ indica le stringhe che hanno 2 uni al loro interno
• $n$ le stringhe che hanno un solo 1
• 1 è la stringa senza 1

Vediamo una soluzione che non fa uso del backtracking:

def bk1(n, k, sol = None):
	if sol is None:
		sol = []
 
	if len(sol) == n:
		if sol.count('1') <= k:
			print(''.join(sol))
		return
 
	sol.append('0')
	bk1(n, k, sol)
	sol.pop()
 
	sol.append('1')
	bk1(n, k, sol)
	sol.pop()

Questa soluzione ha una complessità di $\Theta (2^n\cdot n)$ perché non tagliamo i rami che non ci servono, esploriamo tutto l’albero e ad ogni foglia controlliamo se va bene stamparla oppure no.

Vediamo invece come evitare di controllare rami inutili alla soluzione, ovvero quelli che contengono più di $k$ 1:

def bk2(n, k, tot1 = 0, sol = None):
	if sol is None:
		sol = []
	
	if len(sol) == n:
		print(''.join(sol))
		return
		
	sol.append('0')
	bk2(n, k, tot1, sol)
	sol.pop()
 
	if tot1 < k:
		sol.append('1')
		bk2(n, k, tot1 + 1, sol)
		sol.pop()

In questo modo evitiamo di percorrere i rami inutili visti nell’immagine prima.

Attenzione

Ci serve una variabile per contare gli 1, non possiamo fare count('1') altrimenti ogni stringa avrebbe costo $O(n)$

Tempi delle due soluzioni a confronto con $n=24,k=2$:

Perché andiamo a risparmiare così tanto tempo?

Si consideri un algoritmo di enumerazione basato sul backtracking dove l’albero di ricorsione ha altezza $h$, il costo di una foglia è $g(n)$ e il costo di un nodo interno è di $O(f(n))$.

Se l’algoritmo gode della seguente proprietà:

• Un nodo viene generato solo se ha la possibilità di portare ad una foglia da stampare

Allora la complessità dell’algoritmo è proporzionale al numero di cose da stampare $S(n)$, più precisamente:

$$O(S(n)\cdot h\cdot f(n)+S(n)\cdot g(n))$$

• Il costo totale dei nodi foglia sarà $O(S(n)\cdot g(n))$ perché verranno generate soltanto le foglie da stampare
• I nodi interni dell’albero che verranno generati saranno $O(S(n)\cdot h)$ perché se un nodo esiste allora appartiene ad un percorso che porta ad una foglia, quindi abbiamo foglie $\times$ altezza

Esercizio 3

Progettare un algoritmo che, presi due interi $n$ e $k$ con $0\le k\le n$ stampi tutte le stringhe che contengono esattamente $k$ uni.

Ad esempio per $n=6,k=3$ delle $2^6=64$ stringhe lunghe $n$ bisogna stampare soltanto le seguenti 20:

def bk3(n, k, tot1 = 0, sol = None):  
    if sol is None:  
        sol = []  
  
    if len(sol) == n:  
        print(''.join(sol))  
        return  
  
    #remain = n - len(sol) - 1 caratteri che mi rimangono da aggiungere  
    if n - len(sol) - 1 + tot1 >= k:  
        sol.append('0')  
        bk3(n, k, tot1, sol)  
        sol.pop()  
  
    if tot1 < k:  
        sol.append('1')  
        bk3(n, k, tot1 + 1, sol)  
        sol.pop()

Esercizio 4 (settembre 2020)

Progettare un algoritmo che, dato un intero $n$, stampi tutte le stringhe sull’alfabeto dei 3 simboli $a,b,c$ in cui il numero delle $b$ supera quello di ciascuno degli altri due simboli.

Ad esempio per $n=2$ l’algoritmo deve stampare la sola stringa $bb$ mentre per $n=3$ le stringhe da stampare sono:

• $bbb,abb,bab,bba,cbb,bcb,bbc$

def bk4(n, na = 0, nc = 0, sol = None):  
    if sol is None:  
        sol = []  
  
    if len(sol) == n:  
        print(''.join(sol))  
        return  
  
    sol.append('b')  
    bk4(n, na, nc, sol)  
    sol.pop()  
  
    # Caratteri che mi mancano da aggiungere sono maggiori del numero della  
    # stringa con un carattere a aggiunto    
    if n - (na + nc + 1) > na + 1:  
        sol.append('a')  
        bk4(n, na + 1, nc, sol)  
        sol.pop()  
  
    # Caratteri che mi mancano da aggiungere sono maggiori del numero della  
    # stringa con un carattere c aggiunto    
    if n - (na + nc + 1) > nc + 1:  
        sol.append('c')  
        bk4(n, na, nc + 1, sol)  
        sol.pop()

Esercizio - Marzo 2023

Dati tre interi $n,k,T$ positivi con $T\le nk$ definiamo valida una sequenza di lunghezza $n$ con interi tra $0$ e $k$ la somma di cui elementi è $T$.

Ad esempio per $n=6,k=4,T=12$ allora la sequenza $132042$ è valida mentre $121213$ non è valida.

Progettare un algoritmo che dati gli interi $n,k,T$ stampi tutte le sequenze valide.

L’algoritmo deve avere complessità $O(n\cdot k\cdot S(n,k))$ dove $S(n,k)$ è il numero di sequenze valide esistente.

def bk(n, k, T, somma = 0, sol=[]):  
  
    if len(sol) == n:  
        print(''.join(sol))  
        return  
  
    for new_char in range(k + 1):  
        if new_char + somma + (n - len(sol)-1) * k >= T and somma + new_char <= T:  
            sol.append(str(new_char))  
            bk(n, k, T, somma + new_char, sol)  
            sol.pop()

• Con la prima condizione dell’if sto controllando se aggiungendo il nuovo elemento posso comunque raggiungere il valore T con i restanti elementi.
• La seconda mi permette di non superare T

Esercizio

Progettare un algoritmo che data una stringa X lunga $n$ sull’alfabeto ternario $\{0,1,2\}$ stampi tutte le stringhe che è possibile ottenere da X sostituendo il simbolo $\ast$ ad alcuni dei suoi caratteri in modo che i caratteri rimanenti risultino in ordine strettamente crescente.

Ad esempio:

• X = “021” allora dobbiamo stampare: ***, 0**, 02*, 0*1, *2*, **1
• X = “2110” allora stampiamo: ****, 2***, *1**, **1*, ***0

L’algoritmo deve avere una complessità di $O(nS(n))$ dove $S(n)$ è il numero di stringhe da stampare.

# Sol Professore
def esAstMonti(X, p = '*', sol = []):  
    if len(sol) == len(X):  
        print(''.join(sol))  
        return  
  
    sol.append('*')  
    esAstMonti(X, p, sol)  
    sol.pop()  
    i = len(sol)  
    if p == '*' or X[i] > p:  
        sol.append(X[i])  
        esAstMonti(X, X[i], sol)  
        sol.pop()
 
# Sol mia più brutta perchè non ho pensato al fatto che abbiamo solo 3 caratteri (in teoria funziona anche con numeri da 0 a 9 (?))
def esAst(seq, max='-1', sol=None):  
    if sol is None:  
        sol = []  
  
    if len(sol) == len(seq):  
        print(''.join(sol))  
        return  
  
    sol.append('*')  
    esAst(seq, max, sol)  
    sol.pop()  
  
    i = len(sol)  
  
    if max < seq[i]:  
        sol.append(seq[i])  
        esAst(seq, seq[i], sol)  
        sol.pop()

Esercizio Ottobre 2020

Progettare un algoritmo che, data una stringa X di lunghezza n, sull’alfabeto dei 3 simboli 0, 1 e 2, stampa tutte le stringhe di lunghezza n sullo stesso alfabeto che differiscono da X in ciascuna posizione. L’algoritmo proposto deve avere complessità $O(nD(n))$ dove $D(n)$ è il numero di stringhe da stampare.

Ad esempio se X=“020” l’algoritmo deve stampare le 8 stringhe: 101, 102, 111, 112, 201, 202, 211, 212

def esOtt2020(X, sol = []):  
    if len(sol) == len(X):  
        print(''.join(sol))  
        return  
  
    for char in ['0','1','2']:  
        if char != X[len(sol)]:  
            sol.append(char)  
            esOtt2020(X, sol)  
            sol.pop()

Esercizio Gennaio 2021

Progettare un algoritmo che, dato un intero n, stampa tutte le stringhe binarie lunghe $n$ in cui non appaiono mai 3 simboli uguali consecutivi. L’algoritmo proposto deve avere complessità $O(nD(n))$ dove $D(n)$ è il numero di stringhe da stampare. Ad esempio per $n=3$ l’algoritmo dve stampare, non necessariamente nello stesso ordine, le seguenti 6 stringhe: 001, 010, 011, 100, 101, 110

def esGenn2021(n, sol = []):  
    if len(sol) == n:  
        print(''.join(sol))  
        return  
  
    i = len(sol)  
    for char in ['0', '1']:  
        if i >= 2:  
            if sol[i-1] != char or sol[i-2] != char:  
                sol.append(char)  
                esGenn2021(n, sol)  
                sol.pop()  
        else:  
            sol.append(char)  
            esGenn2021(n, sol)  
            sol.pop()

Esercizio es

Progettare un algoritmo che, dato un intero $n$, stampa tutte le stringhe binarie lunghe $2n$ per le quali la somma dei primi $n$ bit è uguale alla somma degli ultimi $n$ bit.

Ad esempio per $n=2$, deve stampare:

• 0101, 0110, 1010, 1001, 0000, 1111

def esEsame(n, sum=0, sol = None):  
    if sol is None:  
        sol = []  
  
    if len(sol) == 2*n:  
        print(''.join(sol))  
        return  
  
    for char in [0,1]:  
        if len(sol) < n:  
            sol.append(str(char))  
            esEsame(n, sum + char, sol)  
            sol.pop()  
        else:  
            if sum - char <= 2*n - len(sol) - 1 and sum-char >= 0:  
                sol.append(str(char))  
                esEsame(n, sum - char, sol)  
                sol.pop()

Esercizio Gennaio 2023

Data una stringa binaria $s$, la differenza tra il numero di 1 e il numero di 0 nelle prime $i$ posizioni di $s$ è detto vantaggio alla posizione $i$ in $s$.

Ad esempio per $s=010010111000$ il vantaggio nelle dodici posizioni è rispettivamente: -1, 0, -1, -2, -1, -2, -1, 0, 1, 0, -1, -2

Dati due interi positivi $n$ ed $a$ con $a\ge 1$ definiamo con $S(n,a)$ l’insieme di stringhe binarie di lunghezza $n$ il cui vantaggio in ogni posizione cade nell’intervallo che va da $-a$ ad $a$.

Ad esempio con $S(5,2)=\{01010,01011,01100,01101,10010,10011,10100,10101\}$

L’algoritmo, dati $n$ ed $a$ deve stampare tutte le stringhe in $S(n,a)$.

def esGenn2023(n, a, diff = 0, sol = None):  
    if sol is None:  
        sol = []  
  
    if len(sol) == n:  
        print(''.join(sol))  
        return  
  
    for char in [0,1]:  
        d = -1 if char == 0 else 1  
        if -a < diff < a:  
            sol.append(str(char))  
            esGenn2023(n, a, diff + d, sol)  
            sol.pop()