Logica del Primo Ordine - FOL

Introduzione

Per logica intendiamo un linguaggio formale usato per rappresentare informazioni e derivare conseguenze.

Ogni logica è definita da una sintassi e una semantica

• Sintassi - È l’insieme delle sequenze finite di simboli ammesse dal linguaggio ovvero le formule, ogni simbolo usato nelle formule appartiene ad un insieme cioè l’alfabeto.
• Semantica - Definisce il significato di ogni formula della logica, ovvero la sua verità in diversi mondi possibili.

Esempio - Il linguaggio dell’aritmetica

Sintassi:

• $x+2\ge y$ è una formula ma $x2+y\ge$ non lo è

Semantica:

• $x+2\ge y$ è vero se il valore di $x+2$ non è minore del valore di $y$
• $x+2\ge y$ è vero in un mondo dove $x=7$ e $y=1$
• $x+2\ge y$ è falso in un mondo dove $x=0$ e $y=6$

Dato mondo $m$ e la formula $\rho :m\models \rho$ se $\rho$ è vera nel mondo $m$ si dice che $m$ è modello di $\rho$

Sintassi - in breve

La sintassi definisce la struttura delle formule, per definire la sintassi dobbiamo stabilire:

• Quali simboli appartengono all’alfabeto della logica
• Quali sequenze finite di simboli compongono il linguaggio (formule)

La sintassi definisce soltanto quali sono le formule ma non il loro significato.

Semantica - in breve

Definisci il significato delle formule ovvero la sua verità nei diversi mondi. In ogni mondo possibile una formula può essere vera o falsa.

Di solito si dà significato alle formule più semplici, quelle atomiche ovvero che non possono essere ridotte ulteriormente e poi usando le regole della logica si stabilisce un significato alla altre formule.

È quindi simile alla valutazione di un’espressione algebrica.

Sintassi

L’alfabeto della FOL è dato da:

• Un insieme $\mathcal{V}$ di variabili
• Un insieme $\mathcal{F}$ di simboli di funzione, a ciascuno di questi è associato un numero di argomenti detto arità
• Un insieme $\mathcal{P}$ di simboli di predicato, anche loro hanno associato un numero di argomenti detto arità
• Connettivi logici $\neg ,\vee ,\wedge ,\to ,\iff$
• Quantificatori $\forall ,\exists$ rispettivamente quantificatore universale e esistenziale
• Simboli speciali (, ) e ,

Omettiamo di inserire ogni volta il simbolo = nei predicati

• Quando ci riferiamo ad un simbolo di funzione $f$ o predicato $p$ di arità $k$ lo indichiamo con $f/k$ o $p/k$

• Se un simbolo di funzione ha arità zero viene detto simbolo di costante

• Se un simbolo di predicato ha arità zero viene detto lettera preposizionale

In generale possiamo intendere i simboli di funzione come degli “oggetti” del mondo (dominio) e i predicati come delle funzioni che ci restituiscono True o False

Nei seguenti esempi diamo significato ad alcuni predicati e funzioni ma vedremo meglio avanti cosa significa.

Esempi - simboli funzione

• zero/0 è un simbolo di costante che usiamo per indicare il numero naturale 0
• succ/1, vuole un argomento quindi ad esempio succ(X) indicherà il numero X + 1
• socrate/0 è un simbolo di costante, l’individuo “Socrate”
• padre/1 prende un argomento X e restituisce il suo padre. padre(X)

Esempi - simboli di predicato

• doppio/2, lo usiamo con doppio(X, Y) e ritorna true se il numero naturale Y è il doppio del numero naturale X
• somma/3. somma(X, Y, Z) e ritorna True se il numero naturale Z è la somma dei numeri naturale X e Y.
• uomo/1. uomo(X) ritorna True se l’individuo X è un uomo
• mortale/1. mortale(X) ritorna True se l’individuo X è mortale

Formule

Grazie all’alfabeto adesso siamo in grado di definire il linguaggio della FOL, ci servono due step:

• Definire un linguaggio intermedio chiamato linguaggio dei termini
• Definire il linguaggio delle formule ovvero quello della FOL utilizzando quello dei termini

Essenzialmente utilizziamo quello delle formule su una formula e se questa è complessa useremo quello dei termini sui suoi termini, in modo induttivo.

Termini

L’insieme dei termini è definito come segue:

• Ogni variabile in $\mathcal{V}$ è un termine
• Ogni simbolo di costante in $F$ è un termine
• Se $f\in \mathcal{F}$ è un simbolo di funzione di arità $n>0$ e $t_1,\dots ,t_n$ sono termini, allora anche $f(t_1,\dots ,t_n)$ è un termine

Esempio

Abbiamo $\mathcal{F}=\{\text{zero/0, succ/1, socrate/0, padre/1}\}$ e le variabili MiaVariabile, X. I seguenti simboli sono termini:

• zero
• MiaVariabile
• succ(zero)
• padre(padre(socrate))
• padre(succ(X))
• succ(succ(zero))

Formule

L’insieme delle formule è definito in modo induttivo usando quello dei termini:

• Se $p$ è un simbolo di predicato di arità $n$ e $t_1,\dots ,t_n$ sono termini allora $p(t_1,\dots ,t_n)$ è una formula, detta formula atomica
• Se $\varphi ,\sigma$ sono formule allora lo sono anche
  • $\neg \varphi ,\varphi \vee \sigma ,\varphi \wedge \sigma ,\varphi \to \sigma$…
• Se $\varphi$ è una formula e X una variabile allora sono formule anche:
  • $\forall X\varphi ,\exists X\varphi$

Per il predicato di uguaglianza non scriveremo $=(X,Y)$ ma $X=Y$

Esempi di formule

Siano:

• $\mathcal{F}=\{\text{zero/0, succ/1, socrate/0, padre/1}\}$
• $\mathcal{P}=\{\text{doppio/2, somma/3, uomo/1, mortale/1}\}$

Le seguenti sequenze di simboli sono formule:

• doppio(succ(succ(zero)), X)
• $\exists X$ doppio(succ(succ(zero)), X)
• somma(succ(zero), zero, succ(zero))

Mentre non sono formule:

• succ(zero)
• mortale(mortale(socrate))
• padre(mortale(X))
• $\exists X$ padre(X)

Semantica

Per costruire la semantica dobbiamo:

• Definire la nozione di intepretazione ovvero la valutazione delle formule atomiche
• Definire come viene valutata una formula, data una particolare interpretazione
• Stabilire il significato di ogni formula senza riferimento a particolari intepretazioni

Siccome nel nostro linguaggio abbiamo sia termini che formule distinguiamo la valutazione in livello dei termini e livello delle formule. Ci servono quindi due nozioni di valutazione:

• Valutazione dei termini
  • Valutazione dei termini atomici divisa in
    • Pre Interpretazione che usiamo per valutare i simboli di funzione
    • Assegnamento di variabili usata per valutare le variabili
  • Valutazione di Funzioni complesse, si usa in modo induttivo la valutazione dei termini
• Valutazione delle formule
  • Si valutano le formule atomiche tramite un’interpretazione
  • Si valutazione le formule complesse in modo induttivo usando la valutazione di quelle atomiche

Esempio

Siano:

• $\mathcal{F}=\{\text{socrate/0, padre/1}\}$
• $\mathcal{P}=\{\text{uomo/1, mortale/1}\}$

Vogliamo valutare la formula:

$$(\forall X\text{uomo(X)}\to \text{mortale(padre(X))})\wedge \text{uomo(socrate)}$$

Eseguiamo l’interpretazione in modo non formale tramite un esempio, dopo con la valutazione si rivedono queste cose ma in modo formale

Dobbiamo definire, per quanto riguarda i termini:

• Un insieme $\mathcal{D}$ di oggetti del mondo (dominio)
• Una corrispondenza dai simboli di funzione a funzioni su $\mathcal{D}$ di opportuna arità
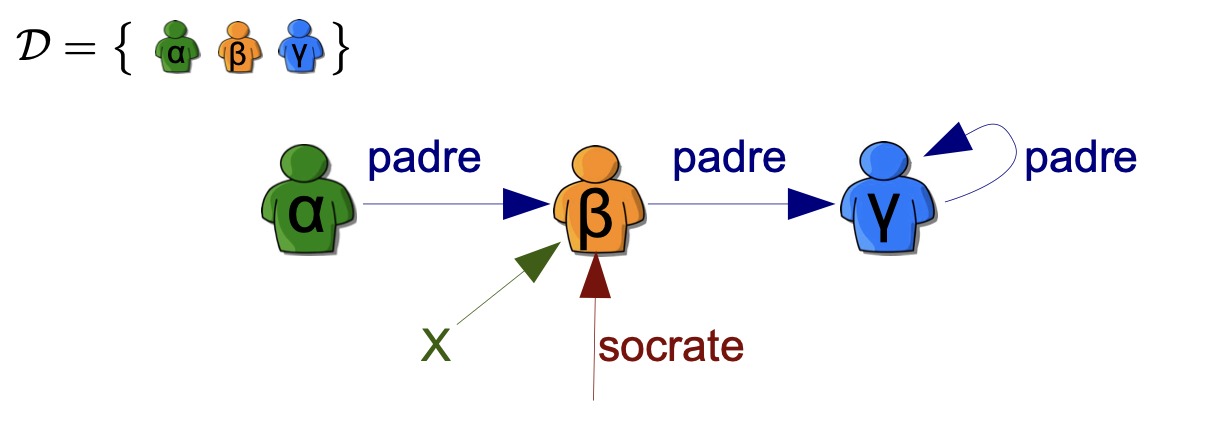
  • socrate/0 che è un simbolo di costante è una funzione $D^0\to D$ infatti non prende argomenti ($D^0$) e restituisce un elemento del dominio (socrate)
  • padre/1 che è un simbolo di funzione 1-aria è una funzione $D^1\to D$ dato che prende come argomento un elemento del dominio e restituisce sempre un elemento del dominio.
• Una corrispondenza dalle variabili a elementi di $\mathcal{D}$, associare quindi ad ogni variabile un elemento

Quindi una possibile interpretazione a livello dei termini è la seguente:

Per quanto riguarda il livello delle formule:

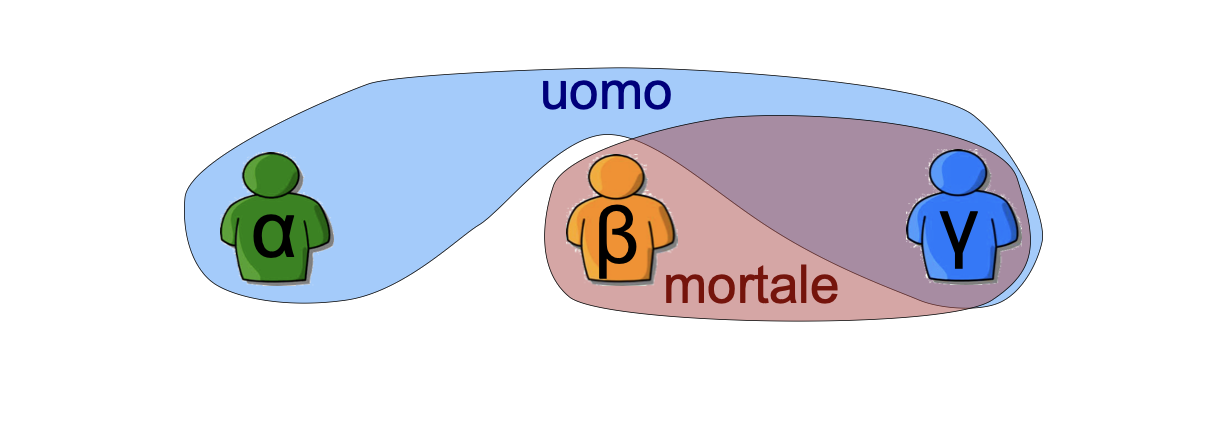
• Ci serve una corrispondenza dai simboli di predicato a relazioni su $\mathcal{D}$ di opportuna arità
  • uomo/1 è una relazione 1-aria su $\mathcal{D}$, è infatti un sottoinsieme del dominio che soddisfa determinate regole (in questo caso essere un uomo)

Una possibile interpretazione è la seguente:

Quindi riassumendo entrambi i livelli, otteniamo:

Adesso è possibili eseguire la valutazione

Valutazione dei Termini

Prima abbiamo detto che ci server la preinterpretazione per valutare i termini. Definiamola in modo formale e non con un esempio come prima.

Dobbiamo definire:

• Un insieme non vuoto $\mathcal{D}$ ovvero il dominio di interpretazione che può essere sia finito che non
• Una corrispondenza che associa ad ogni simbolo di funzione $f/n\in \mathcal{F}$ di arità $n\ge 0$ una funzione del tipo: $D^n\to D$ che denotiamo con preI(f). Se il simbolo di costante ha arità 0 allora la funzione associa al simbolo di costante un elemento di D

Diamo quindi una preinterpretazione preNAT per $\mathcal{F}$ come segue:

• Per dominio prendiamo l’insieme dei numeri interi non negativi
• $\text{preNAT(zero)}=0\in \mathcal{D}$
• $\text{preNAT(succ)}$ è la funzione $D\to D$ definita come:
  • preNAT(succ)(0)=1
  • preNAT(succ)(1)=2
  • …
  • preNAT associa quindi al simbolo unario succ/1 una funzione del tipo $D^1\to D$ e quindi per noi codifica la funzione “successore” sugli interi non negativi

Passiamo poi all’assegnamento delle variabili.

Sia $\mathcal{V}$ un insieme di variabili e sia preI una preinterpretazione con dominio $\mathcal{D}$, un assegmanto delle variabili $mathcalV$ per preI è una funzione $\mathcal{V}\to \mathcal{D}$ che associa ad ogni variabile un elemento del dominio di intepretazione di preI

Esempio

Sia $\mathcal{V}=\{X,Y,Z\}$, consideriamo la preinterpreazione preNAT in cui il dominio $\mathcal{D}$ è l’insieme degli interi non negativi, definiamo la funzione $W$ tale che:

• $W(X)=3$
• $W(Y)=6$
• $W(Z)=4$ Questa funzione è il nostro assegmanto delle variabili $\mathcal{V}$ per preNAT

---

Adesso che abbiamo definito la preintepreazione dei termini e l’assegnamento delle variabili, possiamo valutare i termini.

Definizione - Dati $\mathcal{V},\mathcal{F}$ e sia $\mathcal{T}$ l’insieme di tutti i termini che possono essere generati da $\mathcal{V}$ e $\mathcal{F}$ e dati una pre interpretazione preI sul dominio $\mathcal{D}$ e un assegnamento di variabili $S$ per preI, la funzione:

$${\text{pre-eval}}^{\text{preI, S}}:\mathcal{T}\to \mathcal{D}$$

è definita in modo induttivo seguendo la struttura dei termini:

• Se troviamo un termine atomico (caso base) abbiamo due opzioni:
  • Se $X$ è una variabile allora ${\text{pre-eval}}^{\text{preI, S}}(X)=S(X)$
  • Se $c$ è un simbolo di costante allora ${\text{pre-eval}}^{\text{preI, S}}(c)=\text{preI}(c)$
• Se troviamo un termine complesso allora siamo nel caso induttivo
  • Se $f$ è un simbolo di funzione di arità $n>0$ e $t_1,\dots ,t_n$ sono termini allora:

$${\text{pre-eval}}^{\text{preI, S}}(f(t_1,\dots ,t_n))=\text{preI}(f)({\text{pre-eval}}^{\text{preI,S}}(t_1),\dots ,{\text{pre-eval}}^{\text{preI,S}}(t_n))$$

Esempio

• $\mathcal{V}=\{X,Y,Z\}\mathcal{F}=\{\text{zero/0, succ/1}\}$
• Usiamo la preinterpretazione vista prima preNAT e l’assegnazione delle variabili $W$: $W(X)=3,W(Y)=6,W(Z)=4$

L’insieme $\mathcal{T}$ dei termini che possiamo generare è:

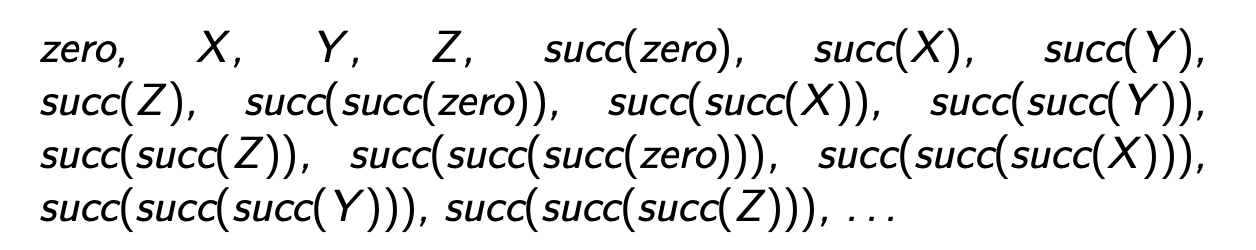
Valutazione la seguente formule:

$${\text{pre-eval}}^{\text{preNAT,W}}(succ(succ(X)))$$

Valutazione delle Formule

Per valutare le formule ci serve un’interpretazione I che è costituita da:

• Una preinterpretazione preI che a sua volta definisce un dominio $\mathcal{D}$ e una funzione su $\mathcal{D}$ per ogni simbolo di funzione
• Una funzione che associa ad ogni simbolo di predicato p/n una relazione $I(p)$ su ${\mathcal{D}}^n$:

$$I(p)\subseteq \underset{\text{n volte}}{\underbrace{\mathcal{D}\times \cdots \times \mathcal{D}}}$$

Quindi ad esempio questa funzione deve assegnare al simbolo di = la relazione $\{(d,d)|d\in \mathcal{D}\}\subseteq \mathcal{D}\times \mathcal{D}$, ovvero tutte le coppie di elementi del dominio uguali fra loro.

Esempio

Siano $\mathcal{F}=\{\text{zero/0, succ/1}\}\mathcal{P}=\{\text{doppio/2, somma/3}\}$, definiamo l’interpretazione NAT in questo modo:

• Utilizza la preinterpretazione preNAT vista prima per le funzioni
• NAT(doppio) = $\{(0,0),(1,2),(2,4),\dots \}=\{(x,y)|y=2x\}$
• NAT(somma) = $\{(0,0,0),(0,1,1),(1,0,1),(1,1,2),\dots \}=\{(x,y,z)|z=x+y\}$

---

Quindi avendo un’interpretazione e un assegnamento di variabili per la preinterpretazione possiamo definire la valutazione delle formule:

Definizione - Siano dati $\mathcal{V},\mathcal{F},\mathcal{P}$ e sia $\varphi$ l’insieme di tutte le formule che possono essere generate da $\mathcal{V},\mathcal{F},\mathcal{P}$.

Sia $I$ una interpretazione su $\mathcal{P}$ che include una preinterpretazione preI su $\mathcal{F}$.

Sia $S$ un assegnamento alle variabili $\mathcal{V}$ per preI.

Definiamo la funzione:

$${\text{eval}}^{I,S}:\varphi \to \{true,false\}$$

Nel seguente modo, sempre per induzione:

• Se troviamo una formula atomica siamo nel caso base
  • Se p/n è un simbolo di predicato e $t_1,\dots t_n$ sono termini allora

$${\text{eval}}^{I,S}(p(t_1,\dots ,t_n))=I(p)({\text{pre-eval}}^{\text{preI,S}}(t_1),\dots ,{\text{pre-eval}}^{\text{preI,S}}(t_n))$$

• Se troviamo una formula complessa allora siamo nel caso induttivo

È praticamente la logica proposizionale

Quando scriviamo S[X/d]indichiamo che “sovrascriviamo” l’assegnamento delle variabili S e all’interno di X inseriamo d

Esempio

Utilizzando sempre la preinterpretazione preNAT su:

• $\mathcal{F}=\{\text{zero/0,succ/1}\}$
• $\mathcal{P}=\{\text{doppio/2, somma/3}\}$

Utilizziamo l’assegnamento $W$ sulle variabili $V=\{X,Y,I,J,K\}$, definito come segue:

• $W(X)=3$
• $W(Y)=6$
• $W(I)=W(J)=W(K)=4$

Quanto vale la formula

$${\text{eval}}^{NAT,W}(\text{doppio(succ(succ(zero)),X)})$$

Altri Esempi

Quando troviamo dei quantificatori abbiamo delle situazioni simili

---

• Una formula $\varphi$ si dice soddisfacibile se esiste un’interpretazione $I$ e un assegnamento di variabili $S$ tale che ${\text{eval}}^{I,S}(\varphi )=\text{true}$
• Una formula $\varphi$ si dice insoddisfacibile se per ogni interpretazione $I$ e assegnamento di variabili $S$ si ha che ${\text{eval}}^{I,S}(\varphi )=\text{false}$
• Una formula $\varphi$ si dice valida se per ogni interpretazione $I$ e assegnamento di variabili $S$ si ha che ${\text{eval}}^{I,S}(\varphi )=\text{true}$

Nelle formule chiuse ovvero dove le variabili sono quantificate, l’assegnamento non gioca alcun ruolo, inoltre per queste formule chiuse abbiamo che:

• Un’interpretazione M per cui ${\text{eval}}^{M,S}(\varphi )=\text{true}$, per ogni assegnamento S si dice modello di $\varphi$.

---

Regole di Precedenza

Nella FOL usiamo le seguenti regole di precedenza:

1. $\neg$
2. $\wedge ,\vee$
3. $\forall ,\exists$
4. $\to$

Ambiguità dei quantificatori

La presenza di più quantificatori che quantificano variabili omonime può creare ambiguità, ad esempio:

$$\forall X\text{ uomo(X)}\wedge \exists X\text{ mortale(X)}\vee X=\text{padre(socrate)}$$

• A quale quantificatore fa riferimento la X in mortale(X)
• A quale quantificatore fa riferimento la X in X = padre(socrate)

Il nome di una variabile quantificata in realtà non gioca alcun ruolo, funzionano come i parametri dei linguaggi di programmazione, questo significa che la formula può essere riscritta evitando ambiguità ma stando comunque attenti alle intenzioni del progettista.

Ad esempio possiamo scrivere le seguenti formule, che sono comunque non equivalenti fra loro:

$$\begin{array}{r}\forall X\text{ uomo(X)}\wedge \exists Y\text{ mortale(X)}\vee Y=\text{padre(socrate)}\\ \forall X\text{ uomo(X)}\wedge \exists Y\text{ mortale(Y)}\vee Y=\text{padre(socrate)}\\ \forall X\text{ uomo(X)}\wedge \exists Y\text{ mortale(Y)}\vee X=\text{padre(socrate)}\\ \forall X\text{ uomo(X)}\wedge \exists Y\text{ mortale(X)}\vee X=\text{padre(socrate)}\end{array}$$

Oppure invece di riscriverla possiamo usare delle parentesi per cancellare le ambiguità:

$$(\forall X\text{ uomo(X)})\wedge (\exists X\text{ mortale(X)}\vee X=\text{padre(socrate)})$$