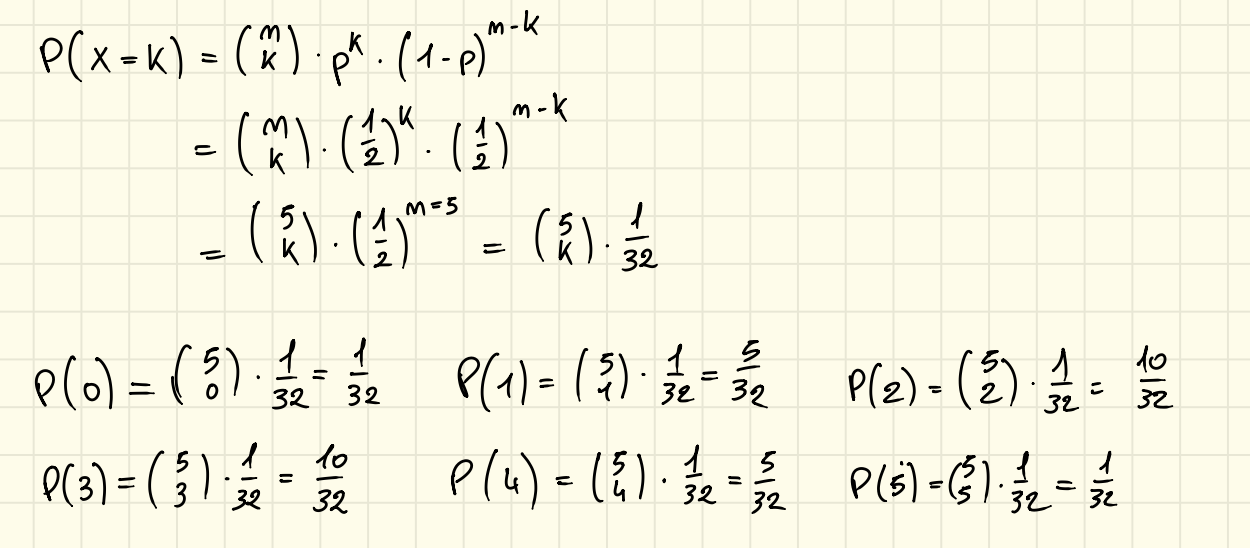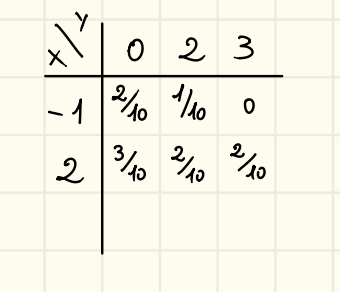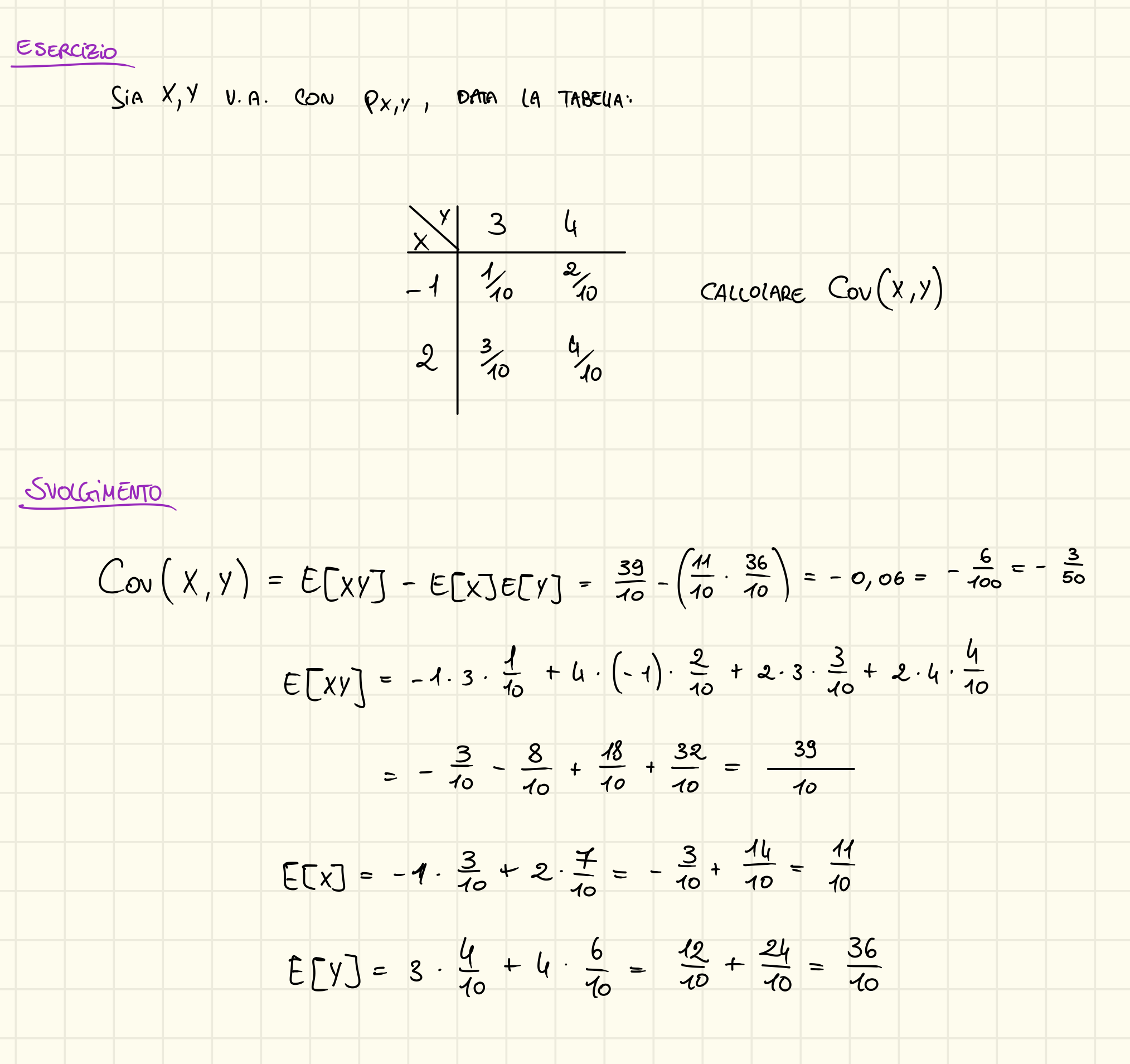Calcolo delle Probabilità

Combinatoria

Principio Fondamentale della Combinatoria

Supponiamo di avere 2 esperimenti, il primo ha n1 esiti possibili mentre il secondo, indipendentemente dall’esito del primo ha n2 esiti possibili. Allora il numero delle coppie $(a_1,a_2)$ possibili con $a_i$ esito dell’esperimento i-esimo è $n_1\cdot n_2$.

Esempio

Se lanciamo un dado 2 volte, la prima volta abbiamo 6 esiti possibili mentre al secondo lancio abbiamo comunque 6 esiti possibili, indipendentemente dal risultato del primo.

Quindi in totale $6\cdot 6=36$ esiti.

$$\#\{(a,b):a=\text{faccia al primo lancio},b=\text{faccia al secondo lancio}\}$$

Notazione #

Il simbolo # davanti ad un insieme indica la sua cardinalità

Esempio

Se abbiamo 140 studenti, in quanti modi possiamo scegliere un rappresentante e un suo vice? Per scegliere il rappresentante abbiamo 140 modi, per il suo vice abbiamo uno studente in meno quindi 139, in totale quindi $140\cdot 139$ esiti.

Principio Fondamentale della Combinatoria (Generale)

Supponiamo di avere R esperimenti. Il primo ha $n_1$ esiti possibili e qualunque sia il suo risultato il secondo avrà sempre $n_2$ esiti. Qualunque sia la realizzazione del secondo il terzo avrà sempre $n_3$ esiti possibili e così via. Allora il numero delle possibili stringhe $(a_1,a_2,\dots ,a_R)$ dove $a_i$ è l’esito dell’esperimento i-esimo è $n_1\cdot n_2\cdot ...\cdot n_R$.

Esempio

Abbiamo 120 ragazzi e 20 ragazze, dobbiamo scegliere un rappresentante e un suo vice in modo che siano di sesso diverso.

Nel primo caso abbiamo 140 esiti possibili, ma nel secondo dipende dall’esito del primo, infatti se abbiamo un rappresentante maschio otteniamo $140\cdot 20$ esiti, mentre se il rappresentante è femmina allora il secondo esperimento ha 120 esiti e quindi $140\cdot 120$.

È caduta l’ipotesi, possiamo però dividere il problema in più sottoproblemi.

Infatti la soluzione che cerchiamo è l’unione di due soluzioni:

$\{(a,b):\text{a rappresentante M., b vice F.}\}\cup \{(a,b):\text{a rappr. F., b vice M}\}$

Il primo ha $120\cdot 20$ esiti mentre il secondo $20\cdot 120$, quindi in totale abbiamo $120\cdot 20+20\cdot 120$ esiti.

Esempio

$\#\{\text{Strighe binarie di lunghezza 5}\}$.

Ad ogni “entrata” ovvero ad ogni carattere della stringa ho sempre 2 possibili input, quindi $2\cdot 2\cdot 2\cdot 2\cdot 2=2^5$.

Esempio

Ho un insieme A di n elementi distinti, quanti sono i suoi sottoinsiemi?

Possiamo utilizzare la stessa formula di prima, quindi $2^n$, questo perché è possibile applicare una bigezione (una funzione biettiva, ha lo stesso funzionamento di una mappa, è come convertire un elemento in un altro) per indicare ogni sottoinsieme con una stringa binaria.

$$\begin{array}{rl}& A=\{a_1,a_2,...,a_n\}\\ & B=\{a_1,a_2,a_4\},B\subset A\\ & \text{Indico B come una stringa, se l’elemento eˋ presente 1, 0 altrimenti}\\ & B=(1,1,0,1,...)\end{array}$$

Quindi la nostra bigezione funziona in modo che $a_i\in B\leftrightarrow x_i=1$.

Esempio

Dobbiamo ordinare:

• 4 libri di matematica
• 3 di chimica
• 2 romanzi

1. In quanti modi possiamo ordinarli sullo scaffale?

   Usando il principio fondamentale otteniamo $9!$ esiti possibili.

2. In quanti modi possiamo ordinarli sullo scaffale, mantenendo vicini quelli della stessa categoria?

   In questo caso non possiamo utilizzare subito il principio fondamentale, perché una volta messo un libro non conosciamo la sua tipologia e ad un certo punto non sapremo come continuare.

   Possiamo però dividere in più sottoproblemi questo caso, prima ordiniamo le categorie.

   Abbiamo 3 categorie, quindi per ordinarle $3!$ modi possibili, teniamo questo numero da parte.

   Poi per ogni categoria vediamo quanti modi abbiamo per ordinarla, quindi matematica $4!$, chimica $3!$ e i romanzi $2!$, mettendo tutto insieme otteniamo $3!\cdot 4!\cdot 3!\cdot 2!$ esiti possibili.

Definizione Permutazioni

Dati $n$ oggetti distinti, le loro permutazioni sono tutti i loro possibili ordinamenti (allineamenti), il numero di questi è $n!$.

Dimostrazione

Per ordinare gli $n$ oggetti scelgo il primo, per fare questo ho $n$ modi, per il secondo ho $n-1$ modi, per il terzo $n-2$ e così via fino a quando non arrivo all’ultimo oggetto che avrà un solo modo per essere ordinato.

$$n!:=\left\{\begin{array}{rl}& 1\text{ se }n=0\\ & 1\ast 2\ast 3\ast \cdots \ast n\text{ se }n=1,2,3,...\end{array}\right\}$$

Esempio

Anagrammi, anche senza senso, della parola “Mela”.

Come prima dobbiamo trovare le permutazioni di 4 elementi distinti, quindi $4!$.

Se dovessimo trovare gli anagrammi di “Emma”? In questo caso abbiamo due elementi uguali, come si procede?

Proviamo a diversificare le M e ottenere $M_1,M_2$, in questo modo otteniamo $4!$ anagrammi, ma se riportiamo le M come prima avremo delle ripetizioni, ad esempio $E{M}_1{M}_{2}A$ e $E{M}_2{M}_{1}A$.

Quindi avendo 2 elementi uguali, per ogni permutazione otteniamo una sua copia, quindi per toglierle tutte dobbiamo calcolare $\frac{4!}{2!}$ dove $4$ indica il numero di elementi e $2$ quello di elementi uguali.

Regola Generale per Permutazioni con elementi uguali

Dati $n$ elementi con $r$ elementi distinti:

• 1° elemento appare $n_1$ volte

• 2° elemento appare $n_2$ volte

• …

• R-esimo elemento appare $n_R$ volte

  $\#\text{permutazioni}\{\frac{n!}{n_1!,n_2!,...,n_R!}\}$

  Esempio con Emma $\frac{4!}{1!\ast 2!\ast 1!}$ Dato che E=1, M=2, A=1.

Esempio

Numero di possibili targhe alfanumeriche di lunghezza 5. Abbiamo 26 lettere e 10 cifre, quindi per ogni entrate 36 input possibili, dato che sono 5 otteniamo $36^5$.

$\#\{\text{Numero di targhe alfanumeriche con simboli distinti di lunghezza 5}\}$ = $36\ast 35\ast 34\ast 33\ast 32$, in questo caso abbiamo usato il principio fondamentale.

$\#\{\text{Targhe di lunghezza 5 con 3 lettere 2 cifre}\}$ Prima scegliamo come posizionare 3 lettere in 5 posti, questo è dato da $\frac{5!}{3!\cdot 2!}$, poi le lettere sono 26 quindi in 3 posizioni abbiamo $26^3$ esiti, mentre per le cifre $10^2$, mettendo tutto insieme otteniamo:

$$\frac{5!}{3!\cdot 2!}\cdot 26^3\cdot 10^2$$

Esempio

Nella finale di 100m, calcolare le possibili classifiche delle nazioni se non ci sono parimerito, con nazione A=3, B=2, C=1, D=2, E=1, F=1

Utilizziamo la formula per il numero di permutazioni con ripetizioni, quindi con 10 partecipanti abbiamo:

$$\frac{10!}{3!\cdot 2!\cdot 2!}$$

Esempio

Riprendiamo un esempio visto prima ma facciamo un’osservazione, scegliamo due rappresentanti in 140 studenti.

$$\#\{(a,b):a\ne b\text{ studenti}\}=140\cdot 139$$

Se utilizziamo le () significa che conta l’ordine, quindi ad esempio la coppia (“Lorenzo”, “Cristina”) è diversa da (“Cristina”, “Lorenzo”) ma noi sappiamo che in realtà sono uguali, quindi in questo caso non ci interessa l’ordine, in questo caso per togliere i doppioni ci basta dividere per due.

Generalizzazione Ho un insieme di $n$ elementi distinti, in quanti modi posso scegliere $k$ elementi distinti e non conta l’ordine?

$$\frac{n(n-1)(n-2)\cdots (n-k+1)}{k!}=\left(\genfrac{}{}{0ex}{}{n}{k}\right)$$

Se invece l’ordine conta utilizziamo il principio fondamentale e quindi non dobbiamo dividere per $k!$. Nella formula vista sopra abbiamo ottenuto il coefficiente binomiale.

Coefficiente Binomiale

Dati $0\le k\le n$ interi:

$$\left(\genfrac{}{}{0ex}{}{n}{n}\right)=\frac{n!}{k!\cdot (n-k)!}$$

Questo ha varie proprietà:

• Se $n=0$ allora anche $k=0$ e $\left(\genfrac{}{}{0ex}{}{0}{0}\right)=\frac{0!}{0!\ast 0!}=1$
• $\forall n$ se $k=0$ ottengo $\left(\genfrac{}{}{0ex}{}{n}{0}\right)=\frac{n!}{0!\ast (n-0)!}=1$
• $\left(\genfrac{}{}{0ex}{}{n}{k}\right)=\left(\genfrac{}{}{0ex}{}{n}{n-k}\right)$

Triangolo di Tartaglia per i Coefficienti Binomiali

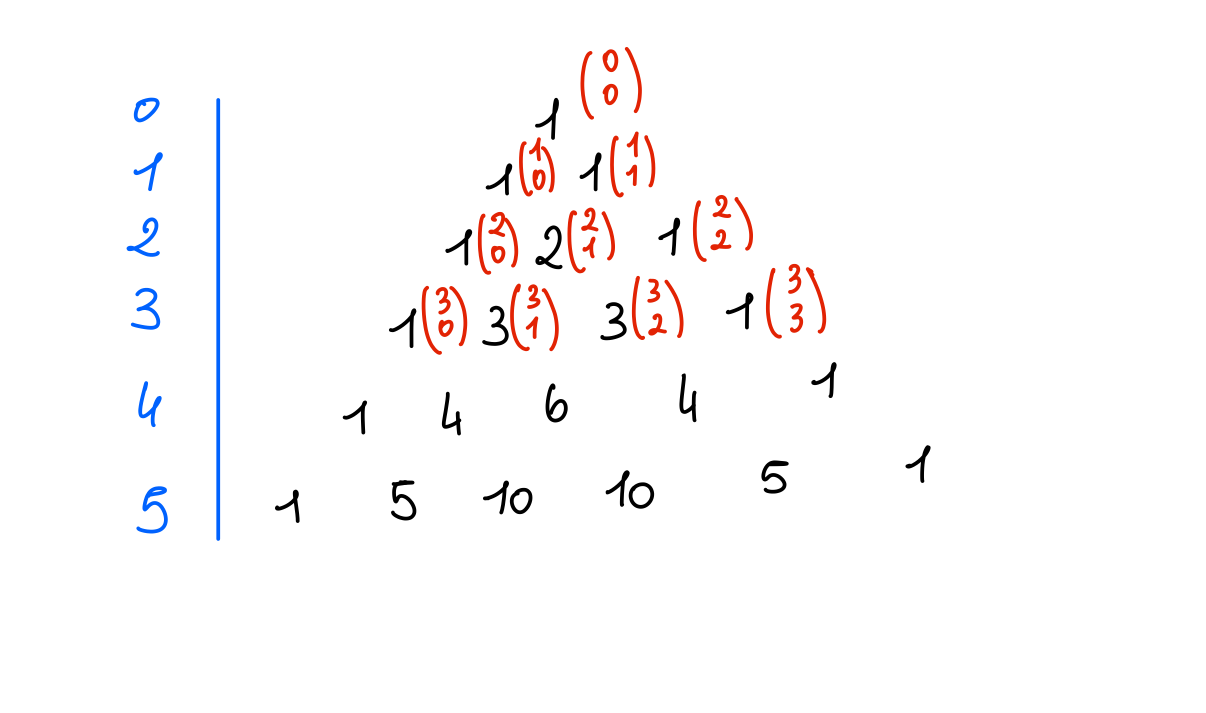
Esempio

Ho 10 studenti, in quanti modi ne posso scegliere 3 se conta l’ordine? E se non conta?

Se conta l’ordine facciamo $10\cdot 9\cdot 8$, se invece l’ordine non conta utilizziamo il C.B. quindi:

$$\left(\genfrac{}{}{0ex}{}{10}{3}\right)=\frac{10!}{3!\cdot 7!}$$

Esempio

Ho 10 informatici, 5 segretari e 20 operai, devo scegliere un gruppo di rappresentanti composto da 3 inf. 2 seg. e 6 op., in quanti modi posso farlo?

$$\frac{10!}{3!\cdot 7!}\cdot \frac{5!}{2!\cdot 3!}\cdot \frac{20!}{6!\cdot 14!}$$

Esempio

In un gruppo da 10 amici devo formare 2 squadre, devo assegnare 5 maglie rosse e 5 maglie blu, in quanti modi posso farlo?

$$\left(\genfrac{}{}{0ex}{}{10}{5}\right)=\frac{10!}{5!\cdot 5!}$$

Infatti le combinazione per assegnare una maglietta sono uguali per entrambe le squadre.

Esempio

Cambiando l’esempio di prima, se voglio formare due squadre scegliendo mano mano ogni membro, in quanti modi posso farlo?

$$\left(\genfrac{}{}{0ex}{}{10}{5}\right)\cdot \frac{1}{2}$$

Vediamo due esempi utili per capire come si svolge.

Esempio 1

Ho 6 studenti e devo dividerli in 2 gruppi, uno da 4 e uno da 2. In questo caso mi basta calcolare i modi di un gruppo, quindi:

$$\left(\genfrac{}{}{0ex}{}{6}{4}\right)oppure\left(\genfrac{}{}{0ex}{}{6}{2}\right)$$

Infatti una volta scelto un gruppo l’altro è già formato. La situazione cambia se i due gruppi hanno la stessa dimensione.

Esempio 2

Dividiamo in 2 gruppi da 3 persone. Se ne scelgo solo 3 per un gruppo, avrò delle ripetizioni, infatti se ad esempio ho come persone A,B,C,D,E,F e scelgo nel primo {A, B, C} nel secondo avrò {D, E, F} ma se come primo gruppo scelgo {D, E, F} come secondo ottengo {A, B, C}, ho ottenuto una ripetizione.

Per eliminarle:

$$\left(\genfrac{}{}{0ex}{}{6}{3}\right)\cdot \frac{1}{2}$$

Esempio

5 studenti vogliono organizzare una festa e si dividono i ruoli:

• C1) Pulire il locale - 2 persone
• C2) Comprare bibite - 2 persone
• C3) Pubblicizzare la festa - 1 persona

Per risolvere scelgo gli studenti per C1, dai rimanenti per C2 e dai rimanenti per C3:

$$\left(\genfrac{}{}{0ex}{}{5}{2}\right)\cdot \left(\genfrac{}{}{0ex}{}{3}{2}\right)\cdot \left(\genfrac{}{}{0ex}{}{1}{1}\right)$$

Osservazione

Svolgendo i calcoli dei coefficienti binomiali visti prima otteniamo:

$$\frac{5!}{2!\cdot 2!\cdot 1!}$$

Che è la stessa formula che utilizziamo per gli anagrammi, infatti possiamo assegnare ad ogni posizione uno studente e ad ogni studente il numero dell’incarico, in questo modo dobbiamo soltanto calcolare gli anagrammi della stringa “13221” (qualsiasi altra combinazione va bene).

Generalizzazione Se abbiamo $n$ oggetti distinti che vogliamo ripartire in $r$ scatole $s_1,s_2,...,s_r$ in modo che $\forall i$ che vanno da $1$ a $r$ nella scatola $s_i$ inserisco l’oggetto $n_i$ dove:

$$n_1+n_2+...+n_r=n$$

Quante sono le ripartizioni possibili?

$$\frac{n!}{n_1!\cdot n_2!\cdot ...\cdot n_r!}=:\left(\genfrac{}{}{0ex}{}{n}{n_1,n_2,...,n_r}\right)$$

E prende il nome di Coefficiente Multinomiale. Quindi se prendiamo l’esempio di prima rappresentando il gruppo che svolge $c_i$ otteniamo $n_1=2,n_2=2,n_3=1,R=3$.

Perché si calcola in questo modo? Applichiamo il principio fondamentale della combinatoria:

1. Scelgo $n_1$ oggetti distinti da mettere in $s_1$. Ho $\left(\genfrac{}{}{0ex}{}{n}{n_1}\right)$ modi

2. Ne scelgo $n_2$ da mettere in $s_2$ dai rimanenti. Ho $\left(\genfrac{}{}{0ex}{}{n-n_1}{n_2}\right)$ modi

3. Per $n_3$ ottengo $\left(\genfrac{}{}{0ex}{}{n-n_1-n_2}{n_3}\right)$ modi

Quindi le ripartizioni totali sono:

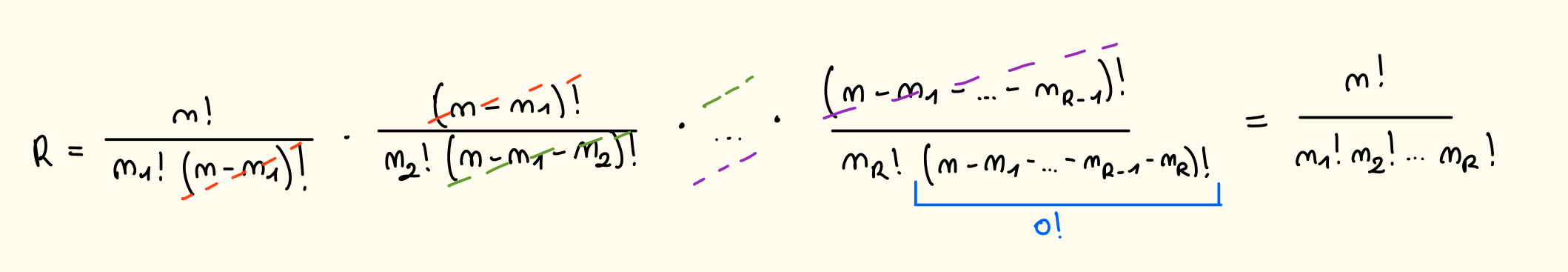
Probabilità

Consideriamo un esperimento (fenomeno con vari esiti) e chiamiamo spazio campionario (S) l’insieme dei possibili esiti dell’esperimento.

Esperimento 1

Lancio di un dado $S=\{1,2,3,4,5,6\}$.

Esperimento 2

Lancio 2 volte una moneta $S=\{(T,T),(T,C),(C,C),(C,T)\}$.

Un evento è descritto matematicamente da un sottoinsieme di $S$, più precisamente dall’insieme degli esiti che lo realizzano.

L’evento “esce un numero pari” è descritto da $\{2,4,6\}\subset S$.

La Famiglia degli eventi = Famiglia dei sottoinsiemi di S. (Questa identità solo se S è numerabile altrimenti vanno fatte delle precisioni, introdurre $\sigma -algebre$).

Proprietà

• Due eventi $E,F\subset S$ si dicono incompatibili se $E\cap F=\varnothing$.

• $S$ come evento è detto evento certo, nel caso del dado l’evento “esce un numero intero” è dato da $S$.

• Dato un evento $E$, l’evento complementare $E^c$ è dato da $E^c=S\backslash E$, ad esempio se l’evento è “esce un numero minore o uguale a 2” l’evento complementare è dato da $\{3,4,5,6\}$.

• Leggi di De Morgan $(A\cup B{)}^c=A^c\cap B^c$ $(A\cap B{)}^c=A^c\cup B^c$

• L’evento impossibile è descritto da $\varnothing$.

Spazio di Probabilità

Definizione Spazio di Probabilità

Uno spazio di probabilità è descritto dalla coppia $(S,P)$ dove S è lo spazio campionario dell’esperimento e P detta funzione di probabilità, è una funzione definita sulla famiglia degli eventi che soddisfa i seguenti assiomi:

1. $P(E)\in [0,1]\forall E$ evento cioè $\forall E\subset S$
2. $P(S)=1$
3. Data una successione $E_1,E_2...$ di eventi 2 a 2 disgiunti vale:

$$P(\bigcup _{i=1}^{\infty }{E}_i)=\sum _{i=1}^{\infty }P(E_i)$$

Questo quando $\forall i\ne j$ e $E_i\cap E_j=\varnothing$ Ovvero $\forall i\ne j$ abbiamo $E_i$ e $E_j$ incompatibili.

Terminologia: Dato $E$ evento, $P(E)$ si dice probabilità dell’evento E.

Proposizione 1

$$P(\varnothing )=0$$

La probabilità dell’evento impossibile è uguale a 0.

Dimostrazione - Utilizzando l’assioma 3

Prendiamo la successione $E_1,E_2,E_3,...$ dove $E_1=\varnothing ,E_2=\varnothing ,E_3=\varnothing ,...$, quindi abbiamo che $\forall i\ne j$ l’intersezione $E_i\cap E_j=\varnothing$.

Per l’assioma 3 $P(\bigcup _{i=1}^{\infty }{E}_i)=\sum _{i=1}^{\infty }P(E_i)$, quindi $P(\varnothing )=\sum _{i=1}^{\infty }P(\varnothing )$, per l’assioma 1 sappiamo che $P(\varnothing )\in [0,1]$.

Supponiamo che $P(\varnothing )\in (0,1]$ allora abbiamo che $\sum _{i=1}^{\infty }P(\varnothing )=+\infty$ e quindi $P(\varnothing )\ne \sum _{i=1}^{\infty }P(\varnothing )$, per esclusione quindi $P(\varnothing )=0$ altrimenti come appena visto otteniamo un valore infinito.

Proposizione 2

Prendiamo un esempio:

• Domani piove con una probabilità 0.3
• Domani c’è il sole con una probabilità 0.6
• Domani nevica con una probabilità 0.1 Qual è la probabilità che piova o che nevichi? 0.3 + 0.1 = 0.4

P soddisfa l’additività finita: Dati $n$ eventi a 2 a 2 incompatibili $E_1,E_2,...,E_n$ vale $P(\bigcup _{i=1}^n{E}_i)=\sum _{i=1}^{n}P(E_i)$

Dimostrazione

Consideriamo la successione $F_1:=E_1,F_2:=E_2,...,F_n:=E_n,F_{n+1}:=\varnothing ,F_{n+2}:=\varnothing$, ovvero hanno dei valori fino ad $n$ e poi sono $\varnothing$.

Dato che la successione è fatta da eventi 2 a 2 incompatibili posso applicare il 3 assioma e otteniamo:

$$P(\bigcup _{i=1}^{\infty }{F}_i)=\sum _{i=1}^{\infty }P(F_i)$$

Che è equivalente a:

$$P(\bigcup _{i=1}^{\infty }{E}_i)=P(E_1)+P(E_2)+...+P(E_n)+P(\varnothing )+...$$

Per la proposizione precedente sappiamo che $P(\varnothing )=0$ quindi tutti i $P(\varnothing )$ sono trascurabili lasciando soltanto:

$$P(\bigcup _{i=1}^n{E}_i)=P(E_1)+P(E_2)+...+P(E_n)$$

Proposizione 3

$$\forall E\subset S\text{ vale }P(E^c)=1-P(E)$$

Dimostrazione

$E$ e $E^c$ sono eventi incompatibili, quindi per l’additività finita abbiamo che $P(E\cup E^c)=P(E)+P(E^c)$ ma sappiamo che $E\cup E^c=S$ quindi possiamo dire che $P(E\cup E^c)=P(S)=1$.

Possiamo scrivere quindi:

$$P(E)+P(E^c)=1\to P(E^c)=1-P(E)$$

Proposizione 4 - Monotonia della Funzione di Probabilità

Dati $E$ e $F$ eventi con $E\subset F$ allora vale $P(E)\le P(F)$.

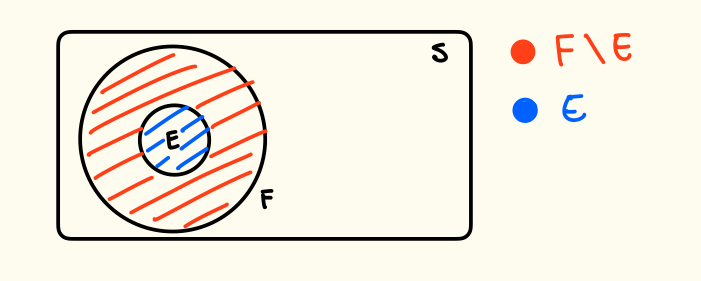
$F=E\cup (F\backslash E)$, quindi $E$ ed $F\backslash E$ sono disgiunti.

Quindi, $P(F)=P(E)+P(F\backslash E)$ dato che per l’assioma 1 $P(F\backslash E)\ge 0$ allora $P(E)+P(F\backslash E)\ge P(E)$.

Proposizione 5

$\forall E,F$ eventi, allora $P(E\cup F)=P(E)+P(F)-P(E\cap F)$, questa è la formula generale, non l’abbiamo usata prima perché nel caso in cui $E,F$ sono disgiunti allora $P(E\cap F)=0$.

Esempio Grafico

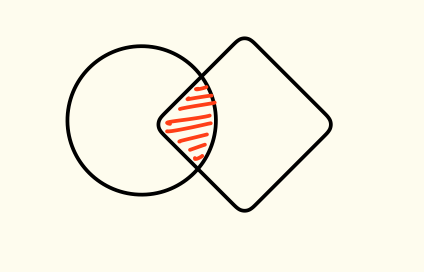
Anche se conosco l’area delle due figure, per conoscere l’area totale devo sottrarre l’area dell’intersezione fra le due.

Dimostrazione

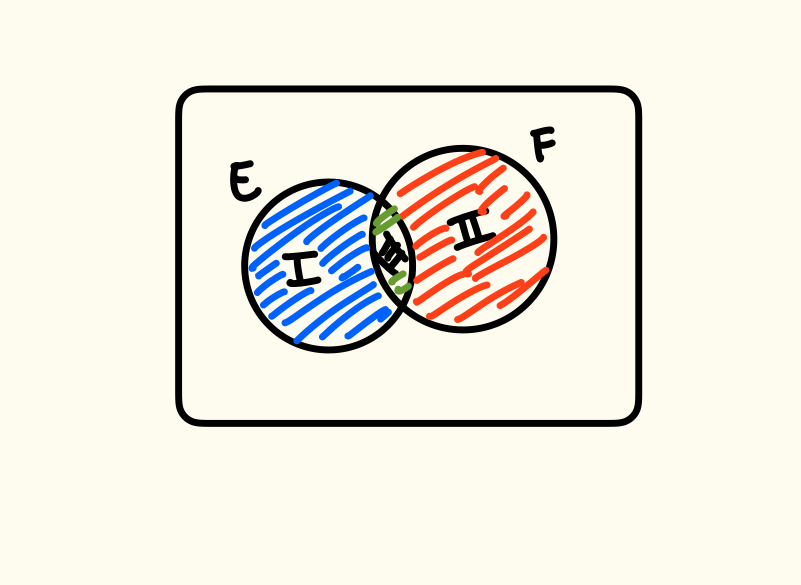
Abbiamo che $I=E\backslash F,II=F\backslash E,III=E\cap F$, gli eventi quindi sono 2 a 2 disgiunti (gli eventi 2 a 2 disgiunti sono le zone I, II e III non E ed F).

Otteniamo che:

• $P(E)=P(I\cup III)=P(I)+P(III)$
• $P(F)=P(II\cup III)=P(II)+P(III)$
• $P(E\cap F)=P(III)$

Sappiamo che:

• $P(E\cup F)=P(I\cup II\cup III)=P(I)+P(II)+P(III)$
• E secondo la proposizione: $P(E\cup F)=P(E)+P(F)-P(E\cap F)$, sostituendo i valori :

$$P(E\cup F)=P(I)+P(III)+P(II)+P(III)-P(III)=P(I)+P(II)+P(III)$$

Abbiamo ottenuto lo stesso risultato.

Esempio

Giulia porta ha 2 libri L1, L2, l’evento E corrisponde a “Le piace L1” mentre F a “Le piace L2”.

• $P(E)=0.5$
• $P(F)=0.4$
• $P(E\cap F)=0.3$ → “Le piacciono entrambi”

Quant’è la probabilità che non le piaccia alcun libro?

• Calcoliamo prima $E\cup F$ che equivale a “Le piace almeno un libro”: $P(E\cup F)=P(E)+P(F)+P(E\cap F)=0.5+0.4-0.3=0.6$
• L’evento complementare di “Le piace almeno un libro” è “Non le piace nessun libro” quindi il risultato finale è:

$$P((E\cup F{)}^c)=1-P(E\cup F)=1-0.6=0.4$$

Infatti:

Dato uno spazio campionario S e due eventi $E,F\subset S$ abbiamo che:

$$x\in E\cup F\iff x\in E\text{ o }x\in F\iff \text{ x realizza almeno uno dei due eventi}$$

Quindi $E\cup F$ significa che “Si verifica E oppure si verifica F” non c’è esclusività, invece $E\cap F$ significa che “Si verifica sia E che F”.

Esempio

Abbiamo un dato truccato dove:

• 1 esce con probabilità $\frac{1}{2}$
• Gli altri numeri con probabilità $\frac{1}{10}$

Quant’è la probabilità che esce un numero dispari? $E=\{1,3,5\}$.

Per additività finita:

$$\underset{\{1\}\cup \{3\}\cup \{5\}\text{ 2 a 2 incompatibili}}{\underbrace{P(E)}}=P(\{1\})+P(\{3\})+P(\{5\})=\frac{1}{2}+\frac{1}{10}+\frac{1}{10}=\frac{7}{10}$$

Esiti su spazi di probabilità con esiti equiparabili

Supponiamo che $|S|<\infty$ quindi abbiamo una situazione del tipo, $S=\{S_1,S_2,\dots ,S_n\}$ con $n$ esiti. Supponiamo che, ad esempio per simmetria, i vari esiti abbiano la stessa probabilità di realizzarsi, sono equiprobabili.

Come modelliamo questo esperimento con uno spazio di probabilità?

• Dato che gli esiti sono tra di loro paritari richiederanno che $P(\{1\})=P(\{2\})=\cdots =P(\{S_n\})=z$, questo valore lo chiameremo $z$.
• Inoltre abbiamo che $$1=P(S)=\underset{S=\{1\}\cup \cdots \cup \{S_n\}\text{ 2 a 2 incompatibili}}{\underbrace{P(\{1\}\cup \cdots \cup \{S_n\})}}=\sum _{i=1}^{n}P(\{S_i\})=n\cdot z$$

Questo perché abbiamo la somma di $n$ valori uguali che valgono tutti $z$.

In questo modo abbiamo provato che $1=n\cdot z$ e quindi $z=\frac{1}{n}$, e dato che sono equiprobabili sappiamo che $\forall i,1\le i\le n,P(\{S_i\})=\frac{1}{n}$.

Proposizione

Se $|S|=n$ e gli esiti sono equipossibili, allora $\forall E,P(E)=\frac{|E|}{|S|}=\frac{\text{\# esiti favorevoli a E}}{\text{\# esiti possibili}}$

Dimostrazione

Dato $E=\bigcup _{S\in E}\{S\}$ gli eventi $\{S\}$, con $S\in E$ sono 2 a 2 incompatibili. Possiamo applicare l’additività finita e ottenere:

$$P(E)=\sum _{S\in E}P(\{S\})=\sum _{S\in E}\frac{1}{n}=\frac{|E|}{n}=\frac{|E|}{|S|}$$

Esempio

Lancio 2 dadi, qual è la probabilità che la somma dei numeri usciti dia 6?

$$\begin{array}{rl}& S=\{(a,b):a,b\in \{1,2,\dots ,6\}\}\\ & a=\text{numero al 1° lancio}\\ & b=\text{numero al 2° lancio}\end{array}$$

Il dado è onesto e quindi tutti i numeri sono equipossibili, quindi:

$$P(E)=\frac{|E|}{|S|}\text{ dove }E\subset S$$ $$\begin{array}{rl}E=\text{"La somma da 6"}& =\{(a,b)\in S:a+b=6\}\\ & =\{(1,5),(2,4),(3,3),(4,2),(5,1)\}\\ & \\ & P(E)=\frac{|E|}{|S|}=\frac{5}{\underset{\text{esiti possbili 2 dadi}}{\underbrace{6\cdot 6}}}=\frac{5}{36}\end{array}$$

Ordine

Conviene non prendere i numeri dimenticando l’ordine, altrimenti gli esiti non sono equipossibili:

$$P(\text{"Sono usciti 2 e 3 in qualunque ordine"})=\frac{2}{36},\{(2,3),(3,2)\}$$ $$P(\text{"Uscito 1 e 1"})=P(\{(1,1)\})=\frac{1}{36}$$

Esempio

Ho un mazzo da 40 carte, estraggo 2 carte senza rimpiazzo, quant’è la probabilità che escano 2 carte di bastoni?

Il mazzo è composto da 4 semi e 10 carte per seme.

• $M$ = Mazzo
• $S=\{(a,b):a,b\in M,a\ne b\}$

Per simmetria ho esiti equiprobabili quindi vale $P(E)=\frac{|E|}{|S|}$.

In questo caso abbiamo che $E=\{(a,b)\in S:a,b\text{ sono di bastoni}\}$, $|S|=40\cdot 39$ che sono i modi possibili per estrarre due carte ed $|E|=10\cdot 9$ che sono i modi possibili per estrarre due carte dello stesso seme.

$$P(E)=\frac{|E|}{|S|}=\frac{10\cdot 9}{40\cdot 39}=\frac{1}{4}\cdot \frac{3}{13}=\frac{3}{52}$$

Approccio Alternativo

$S=\{\{a,b\}:a,b\in M,a\ne B\}$, adesso consideriamo di estrarre 2 carte nello stesso momento e quindi non sono più coppie ordinate, non conta l’ordine.

Gli esiti sono comunque equiprobabili ma adesso per selezionare due carte senza contare l’ordine in tutto il mazzo posso fare $\left(\genfrac{}{}{0ex}{}{40}{2}\right)$ mentre per due carte dello stesso seme $\left(\genfrac{}{}{0ex}{}{10}{2}\right)$ quindi:

$$P(E)=\frac{\left(\genfrac{}{}{0ex}{}{10}{2}\right)}{\left(\genfrac{}{}{0ex}{}{40}{2}\right)}=\frac{3}{52}$$

Esempio Libro

Ho un’urna con 6 palline bianche e 5 nere. Estraggo 3 palline a caso senza rimpiazzo, quant’è la probabilità che esca 1 bianca e 2 nere?

Non ci conviene registrare soltanto il colore delle palline, questo perché rompe la simmetria, ci conviene invece numerarle una per una in modo da distringuerle.

$Urna=U=\{B_1,B_2,B_3,B_4,B_5,B_6,N_1,N_2,N_3,N_4,N_5\}$ abbiamo quindi 11 palline distinguibili.

$S=\{A\subset U:|A|=3\}$, un esempio di esito è $\{B_2,B_4,N_3\}$.

Quindi adesso $S$ ha esiti equiprobabili per simmetria: $P(E)=\frac{|E|}{|S|}$ dove $|S|=\left(\genfrac{}{}{0ex}{}{11}{3}\right)$.

Quanto vale $|E|$? $E=\{A\subset U:|A|=3,\text{A ha una pallina bianca e 2 nere}\}$

$|E|=6\cdot \left(\genfrac{}{}{0ex}{}{5}{2}\right)$ dove $6$ sono i modi per estrarre una pallina bianca e $\left(\genfrac{}{}{0ex}{}{5}{2}\right)$ quelli per scegliere due palline nere senza considerare l’ordine. Quindi:

$$P(E)=\frac{6\cdot \left(\genfrac{}{}{0ex}{}{5}{2}\right)}{\left(\genfrac{}{}{0ex}{}{11}{3}\right)}=\frac{4}{11}$$

Esempio dei Compleanni

A quanto corrisponde la probabilità che due persone condividano lo stesso giorno di compleanno? Prendendo in considerazione soltanto anni da 365 giorni.

$S=\{(x_1,x_2):x_1,x_2\in \{1,2,\dots ,365\}\}$, $E=\{(x_1,x_2)\in S:x_1=x_2\}=\{(1,1),(2,2),\dots ,(365,365)\}$.

Allora $P(E)=\frac{365}{365^2}$ infatti ho una sola coppia fra le 365 di $E$ ed ho $365^2$ per scegliere i compleanni di due persone.

Se abbiamo 3 persone?

$S=\{(x_1,x_2,x_3):x_1,x_2,x_3\in \{1,2,\dots ,365\}\}$, $E=\{(x_1,x_2,x_3)\in S:\exists i\ne j\text{ con }1\le i,j\le 3,x_i=x_j\}$

Ma calcolare tutte le triplette con 3 valori uguali è molto complesso, è invece più semplice calcolare quelle con 3 valori distinti ovvero $E^c$ e poi per calcolare $P(E)$ svolgere $1-P(E^c)$.

$E^c=\{(x_1,x_2,x_3)\in S:x_1,x_2,x_3\text{ sono distinti}\}$, per il principio fondamentale della combinatoria $|E^c|=365\cdot 364\cdot 363$, mentre $|S|=365^3$ e quindi:

$$P(E)=1-\frac{365\cdot 364\cdot 363}{365^3}$$

In Generale per n persone:

$$P(E)=1-\frac{|E^c|}{|S|}=1-\frac{365\cdot 364\cdot \dots .\cdot (365-n+1)}{365^n}$$

Esercizio

Creare una commissione di 5 persone estratte da un gruppo composto da 6 uomini e 9 donne. Se scelgo le persone da bendato, quante sono le probabilità che la commissione sia formata da 3 uomini e 2 donne.

$S=\{A\subset G:|A|=5\}$ dove $G=$ gruppo delle 15 persone totali. Dobbiamo calcolare quindi $P(E)=\frac{|E|}{|S|}$ dove $E=\{A\subset G:|A|=5\wedge \text{A contiene 3U e 2D}\}$.

Come visto in esempi precedenti ci conviene numerare tutte le persone in modo da distinguerle in questo modo otteniamo che per scegliere 3 uomini da un gruppo di 6 posso calcolare $\left(\genfrac{}{}{0ex}{}{6}{3}\right)$ e per le donne $\left(\genfrac{}{}{0ex}{}{9}{2}\right)$ in totale per formare un gruppo da 5 = $\left(\genfrac{}{}{0ex}{}{6}{3}\right)\cdot \left(\genfrac{}{}{0ex}{}{9}{2}\right)$.

$|S|$ è più semplice dato che dobbiamo semplicemente scegliere 5 persone da un gruppo di 15 e quindi $\left(\genfrac{}{}{0ex}{}{15}{5}\right)$, la probabilità è data quindi da:

$$P(E)=\frac{|E|}{|S|}=\frac{\left(\genfrac{}{}{0ex}{}{6}{3}\right)\cdot \left(\genfrac{}{}{0ex}{}{5}{2}\right)}{\left(\genfrac{}{}{0ex}{}{15}{5}\right)}=\frac{240}{1001}$$

Proviamo a tenere conto dell’ordine di scelta:

Allora $S=\{(x_1,x_2,x_3,x_4,x_5):\forall i,x_i\in G,x_1,\dots ,x_5\text{ sono distinti}\}$.

$|S|=15\cdot 14\cdot 13\cdot 12\cdot 11$.

$E=\{(x_1,\dots ,x_5)\in S:\text{ci sono 3u e 2d}\}$.

In questo caso non posso procedere subito con il principio fondamentale dato che se appunto inizio a calcolare $15\cdot 14\cdot ?$ a questo punto non so cosa scegliere, perché dipende dagli esiti precedenti, se ho scelto 2 donne devo scegliere un uomo ma se ho scelto 2 uomini posso scegliere sia una donna che 1 uomo, o altri casi ancora.

Posso però stabilire in che posizione scelgo gli uomini e le donne ad esempio $(U_{\ast },D_{\ast },D_{\ast },U_{\ast },U_{\ast })$ in questo modo posso calcolare tutte le combinazioni di posizioni possibili con il coefficiente binomiale $\left(\genfrac{}{}{0ex}{}{5}{3}\right)=\left(\genfrac{}{}{0ex}{}{5}{2}\right)$ oppure calcolare le permutazioni della stringa e quindi $\frac{5!}{3!\cdot 2!}$, tutti e 3 i modi sono validi.

A questo punto scelgo gli uomini nella cinquina con il principio fondamentale e quindi $6\cdot 5\cdot 4$, e poi scelgo le donne $9\cdot 8$. Mettendo tutto insieme:

$$\frac{5!}{3!\cdot 2!}\cdot 6\cdot 5\cdot 4\cdot 9\cdot 8=\frac{240}{1001}$$

Considerando o meno l’ordine, il risultato NON cambia, avrò sempre le stesse probabilità

Principio di Inclusione / Esclusione

• Con 2 eventi: $P(A\cup B)=P(A)+P(B)-P(A\cap B)$
• Con 3 eventi: $P(A\cup B\cup C)=P(A)+P(B)+P(C)-P(A\cap B)-P(A\cap C)-P(B\cap C)+P(A\cap B\cap C)$
• Con $n$ eventi: (!!! NON FA PARTE DEL PROGRAMMA !!!)

$$P\left(\bigcup _{i=1}^n{E}_i\right)=\sum _{i=1}^{n}P(E_i)-\sum _{i\le i\le j\le n}P(E_i{E}_j)+\sum _{1\le i\le j\le k\le n}P(E_i\cap E_j\cap E_k)\dots (-1{)}^{n}P(E_1\cap E_2\cap E_n)$$

Probabilità Condizionata

Dati $E,F$ eventi con $P(F)>0$, la probabilità di $E$ condizionata a $F$ è definita come $P(E|F)=\frac{P(E\cap F)}{P(F)}$. Per $E,F$ eventi con $P(F)$ positiva.

Si svolge l’esperimento e so che “si verifica F”, questa informazione muta la mia speranza che si verifichi $E$ e la nuova probabilità di $E$ sapendo che si è verificato $F$ è data da $P(E|F)$.

Esempio

Lancio 1 dado.

$E=\text{Esce 1 o 2},P(E)=\frac{2}{6}=\frac{1}{3}$.

Immaginiamo di sapere che si è verificato l’evento $F$ dove $F=\text{Uscito un numero }\le 4$, se so che $F$ si realizza allora so che è uscito o 1 o 2 o 3 o 4. Ho 4 possibili esiti e c’è simmetria.

Quindi in questo modo se si verifica $F$ allora $P(E)=\frac{2}{4}=\frac{1}{2}$, ci aspettiamo quindi $P(E|F)=\frac{1}{2}$, calcoliamolo usando la definizione:

$$\begin{array}{rl}& P(E|F)=\frac{P(E\cap F)}{P(F)}=\frac{\frac{2}{6}}{\frac{4}{6}}=\frac{1}{2}\\ & \\ & S=\{1,2,\dots ,6\}\\ & F=\{1,2,3,4\}\end{array}$$

Proposizione

Se $S$ è finito e ha esiti equiprobabili allora $P(E|F)=\frac{|E\cap F|}{|F|}$ con $E,F$ eventi con $P(F)$ positiva.

Dimostrazione

$P(E|F)=\frac{P\cap F}{P(F)}$ e per ipotesi $P(F)>0$ quindi vale la definizione di $P(E|F)$

$$P(E|F)=\frac{P(E\cap F)}{P(F)}=\frac{\frac{|E\cap F|}{|S|}}{\frac{|F|}{|S|}}=\frac{|E\cap F|}{|F|}$$

Esercizio

Estraggo 3 carte da un mazzo da 40 senza rimpiazzo, sapendo che ho estratto solo carte di bastoni, qual è la probabilità di aver estratto un asso?

$$\begin{array}{rl}& E=\text{Estraggo un asso}\\ & F=\text{Le carte sono di bastoni}\\ & S=\{A\subset M:|A|=3\}\text{ dove M = mazzo, S ha esiti equiprobabili}\\ & \\ & \underset{\text{proposizione precedente}}{\underbrace{P(E|F)=\frac{|E\cap F|}{|F|}}}=\frac{\left(\genfrac{}{}{0ex}{}{9}{2}\right)}{\left(\genfrac{}{}{0ex}{}{10}{3}\right)}=\frac{3}{10}\\ & \\ & \left(\genfrac{}{}{0ex}{}{9}{2}\right)\text{ sono le terne non ordinate di bastoni dove non c’eˋ asso}\end{array}$$

Esempio

Ho un dado truccato dove 1 esce con probabilità $\frac{1}{2}$ mentre gli altri numeri $\frac{1}{10}$, qual è la probabilità che esca $1$ o $2$ sapendo che è uscito un numero $\le 4$.

$$\begin{array}{rl}& S=\{1,2,3,4,5,6\}\\ & E=\{1,2\}\\ & F=\{1,2,3,4\}\\ & \\ & P(E|F)=\frac{P(E\cap F)}{P(F)}=\dots \\ & \\ & E\cap F=\{1,2\},P(E\cap F)=P(\{1\})+P(\{2\})=\frac{1}{2}+\frac{1}{10}=\frac{3}{5}\\ & \\ & P(F)=P(\{1,2,3,4\})=\frac{1}{2}+\frac{3}{10}=\frac{4}{5}\\ & \\ & \cdots =\frac{\frac{3}{5}}{\frac{4}{5}}=\frac{3}{4}\end{array}$$

Regola del Prodotto

Se $P(F)>0,P(E|F)=\frac{P(E\cap F)}{P(F)}$ quindi $P(E\cap F)=P(F)\cdot P(E|F)$

Esempio

Abbiamo un’urna con 10 palline bianche e 4 palline nero, estraggo 2 palline senza rimpiazzo. Qual è la probabilità che siano entrambe bianche? Lo avevamo già risolto con la combinatoria, vediamo senza:

$$\begin{array}{rl}& F=\text{La prima pallina estratta eˋ bianca}\\ & E=\text{La seconda pallina estratta eˋ bianca}\\ & G=E\cap F,P(G)=P(E\cap F)=P(F)\cdot P(E|F)=\frac{10}{14}\cdot \frac{9}{13}\end{array}$$

Dimostrazione

Siano $E_1,\dots ,E_n$ eventi allora $P(E_1\cap \cdots \cap E_n)=P(E_1)\cdot P(E_2|E_1)\cdot P(E_3|E_1\cap E_2)\cdots \cdot P(E_n|E_1\cap \cdots \cap E_{n-1})$ supponendo che $P(E_1>0,P(E_1\cap E_2)>0,\dots ,P(E_1\cap \cdots \cap E_{n-1})>0)$.

Dimostrazione per n=2 già fatta, vediamo con n=3

$$\begin{array}{rl}& n=3\\ & \text{Dobbiamo provare che}\\ & P(E_1\cap E_2\cap E_3)=P(E_1)\cdot P(E_2|E_1)\cdot P(E_3|E_1\cap E_2)\\ & \\ & \text{Per definizione di prob cond.}\\ & \\ & P(E_1)\cdot P(E_2|E_1)\cdot P(E_3|E_1\cap E_2)=P(E_1)\cdot \frac{P(E_2\cap E_1)}{P(E_1)}\cdot \frac{P(E_3\cap E_1\cap E_2)}{P(E_1\cap E_2)}=\dots \\ & \\ & =P(E_1\cap E_2\cap E_3)\end{array}$$

Per $n$ generico è simile.

Esempio

Estraggo 3 carte senza rimpiazzo da un mazzo da 40, qual è la probabilità che la prima carta è di bastoni, la seconda di denari e la terza di bastoni.

$$\begin{array}{rl}& P(G)=?G=\text{1 carta bastoni, 2 denari, 3 bastoni}\\ & \\ & \text{1° Metodo combinatoria}\\ & S=\{(a,b,c):a,b,c\in M,distinti\}\\ & P(G)=\frac{|G|}{|S|}=\frac{10\cdot 10\cdot 9}{40\cdot 39\cdot 38}=\dots \\ & \\ & \text{2° Metodo prob. cond.}\\ & G=E_1\cap E_2\cap E_3\text{ dove}\\ & E_1=\text{prima carta B},E_2=\text{seconda carta D},E_3=\text{terza carta B}\\ & \\ & \text{Per regola prodototto}\\ & P(G)=P(E_1\cap E_2\cap E_3)=P(E_1)\cdot P(E_2|E_1)\cdot P(E_3|E_1\cap E_2)=\\ & =\frac{10}{40}\cdot \frac{10}{39}\cdot \frac{9}{38}=\dots \end{array}$$

Teorema di Bayes

$$P(A|B)\stackrel{\text{Definizione}}{=}\frac{P(A\cap B)}{P(B)}\stackrel{\text{Regola prodotto}}{=}\frac{P(A)\cdot P(B|A)}{P(B)}$$

Enunciato:

$$P(A|B)=\frac{P(A)\cdot P(B|A)}{P(B)}$$

---

Esempio

Ho un’urna con 10 palline di cui 1 d’oro, lancio 1 dado, se esce 1 estraggo 2 palline senza rimpiazzo altrimenti estraggo 1 sola pallina, con che probabilità estraggo la pallina d’oro?

Formula probabilità totale

Dati $E,F$ eventi allora $P(E)=P(F)\cdot P(E|F)\cdot P(F^C)\cdot P(E|F^C)$

Dimostrazione

$E=(E\cap F)\cup (E\cap F^C)$ quindi dato che sono incompatibili $P(E)=P(E\cap F)+P(E\cap F^C)\stackrel{\text{Regola Prodotto}}{=}P(F)\cdot P(E|F)+P(F^C)\cdot P(E|F^C)$.

Se so cosa da il dado allora posso calcolare la probabilità.

$F=\text{Il dado da 1}$, $E=\text{La pallina d’oro viene estratta}$

E quindi per la legge della probabilità totale:

$$\begin{array}{rl}& P(E)=P(F)\cdot P(E|F)\cdot P(F^C)\cdot P(E|F^C)=\dots \\ & \\ & \text{Calcoliamo i valori:}\\ & P(F)=\frac{1}{6}\\ & P(E|F)=\frac{P(E\cap F)}{P(F)}=\frac{9}{\left(\genfrac{}{}{0ex}{}{10}{2}\right)}=\frac{1}{5}\\ & P(F^C)=\frac{5}{6}\\ & P(E|F^C)=\frac{1}{10}\\ & \\ & \text{Quindi:}\\ & \cdots =\frac{1}{6}\cdot \frac{1}{5}+\frac{5}{6}\cdot \frac{1}{10}=\frac{7}{60}\end{array}$$

---

Adesso invece sappiamo che la pallina d’oro è stata estratta, qual è la probabilità che dal dado è uscito 1?

Noi sappiamo calcolare $P(E|F)$ e $P(E|F^C)$ ma adesso vogliamo ottenere $P(F|E)$.

Per il teorema di Bayes:

$$P(F|E)=\frac{P(F\cap E)}{P(E)}=\frac{P(F)\cdot P(E|F)}{P(E)}$$

Quindi:

$$P(F|E)=\frac{P(F)\cdot P(E|F)}{P(E)}=\frac{\frac{1}{6}\cdot \frac{1}{5}}{\frac{7}{60}}=\frac{2}{7}$$

---

Esempio Parte I

In un’agenzia di assicurazioni le persone vengono divise in due categorie: propense e non propense a fare incidenti.

Le persone propense hanno una probabilità di 0.4 di fare un incidente in un anno mentre le non propense 0.2.

Il 30% degli automobilisti è propensa agli incidenti.

Qual è la probabilità che un nuovo cliente abbia un incidente in quell’anno?

$$\begin{array}{rl}& A:=\text{Il nuovo cliente eˋ propenso agli incidenti}\\ & A_1:=\text{Il nuovo cliente ha un incidente in un anno}\\ & P(A_1)=?\\ & P(A_1|A)=0.4,P(A_1|A^C)=0.2,P(A)=0.3\\ & \\ & \text{Per la formula di probabilitaˋ totale:}\\ & P(A_1)=P(A)\cdot P(A_1|A)+P(A^C)\cdot P(A_1|A^C)=0.3\cdot 0.4+0.7\cdot 0.2=0.26=26\%\end{array}$$

Parte II

Sapendo che il cliente ha avuto un incidente in quell’anno, qual è la probabilità che sia propenso agli incidenti?

Quindi

$$P(A|A_1)=\frac{P(A\cap A_1)}{P(A_1)}=\frac{P(A)\cdot P(A_1|A)}{P(A_1)}=\frac{0.3\cdot 0.4}{0.26}=\frac{6}{13}$$

Legge probabilità totale generalizzata

Siano $F_1,\dots ,F_n$ eventi 2 a 2 disgiunti tali che $S=\bigcup _{i=1}^n{F}_i$ allora per ogni evento $E_i$ vale $P(E)=\sum _{i=1}^{n}P(F_i)\cdot P(E|F_i)$.

Esempio con $n=2$

$$P(E)=P(F_1)\cdot P(E|F_1)+P(F_2)\cdot P(E|F_2)$$

Esempio Test Malattia

Abbiamo un esame efficace al 95% quando la malattia è presente, 1% di falsi positivi e il 5x1000 della popolazione ha effettivamente la malattia.

$D=\text{La persona testata ha la malattia}$

$E=\text{Persona eˋ positiva all’esame}$

$$\begin{gathered} \begin{array}{rl}& P(E|D)=0.95\\ & P(E|D^C)=0.01\\ & P(D)=0.005\\ & \text{Qual eˋ la probabilitaˋ che una persona testata abbia la malattia?}\\ & P(D|E)=?\\ & P(D|E)=\frac{P(D\cap E)}{P(E)}=\frac{P(D)\cdot P(E|D)}{P(D) \\ cdotP(E|D)+P(D^C)\cdot P(E|D^C)}=\frac{0.005\cdot 0.95}{0.005\cdot 0.95+0.995\cdot 0.01}=0.323\\ & \text{Quindi se il test dice che siamo malati, lo siamo veramente in un caso su 3 circa.}\end{array} \end{gathered}$$

Il test è buono se $P(D|E)$ è vicina al 100% e anche se $P(D^C|E^C)$ è vicina al 100%.

Questo non è un buon test per la popolazione e la malattia presa in esame, infatti ci sono troppi pochi malati e se vengono effettuati tanti test con questa probabilità di falsi positivi avremo più test sbagliati che veri malati.

Infatti con 995 sani e 5 malati abbiamo molti falsi positivi.

Infatti:

$P(D|E)=\frac{P(D\cap E)}{P(E)}=\frac{\text{\#Persone malate con test positivo}}{\text{\#Persone con test positivo}}$ dove il numero di persone con test positivo (denominatore) è dato da $\text{\#Persone malate con test positivo + \#Persone sane con test positivo}$.

Prendiamo ad esempio 995.000 sani testati allora 9950 sani avranno un test positivo ovvero test sbagliati mentre i malati che sono 5000, solo il 95% ovvero 4750 avranno un test positivo e quindi corretto.

Notiamo quindi che i testi sbagliati 9950 sono molto maggiori rispetto ai test corretti 4750.

Questo test sarebbe più corretto se usato per una malattia con più infetti.

Rapporto a Favore

Definizione: Il rapporto a favore di un evento $A$ è dato da:

$$\frac{P(A)}{P(A^C)}=\frac{P(A)}{1-P(A)}$$

Esempio:

Abbiamo la partita di calcio Italia - Brasile. Se la vittoria dell’italia è data 1 a 5 intendiamo che il rapporto a favore dell’evento “l’italia vince” è $\frac{1}{5}$ e quindi $\frac{P(A)}{P(A^C)}=\frac{1}{5}$.

Data l’espressione possiamo calcolare A:

$$\begin{array}{rl}& P(A)=\frac{1}{5}\cdot (1-P(A))\\ & P(A)=\frac{1}{5}-\frac{P(A)}{5}\\ & \frac{6}{5}P(A)=\frac{1}{5}\\ & P(A)=\frac{1}{6};P(A^C)=\frac{5}{6}\end{array}$$

Esempio di Criminologia

Abbiamo $H$ ipotesi “Mario Rossi è l’assassino”, abbiamo una stima di $P(H)$, ad esempio per Sherlock Holmes $P(H)=0.8$.

Introduciamo una nuova prova $E$ e questa modifica la nostra stima in $P(H|E)$, avendo introdotto una nuova prova, come cambia il rapporto a favore? Questo è dato da:

$$\frac{P(H|E)}{P(H^C|E)}\text{ Mentre prima era }\frac{P(H)}{P(H^C)}$$

Inoltre per il teoria di Bayes sappiamo che:

$$P(H|E)=\frac{P(H)\cdot P(E|H)}{P(E)};P(H^C|E)=\frac{P(H^C)\cdot P(E|H^C)}{P(E)}$$

Quindi il nuovo rapporto è dato da:

$$\frac{P(H|E)}{P(H^C|E)}=\frac{\frac{P(H)\cdot P(E|H)}{P(E)}}{\frac{P(H^C)\cdot P(E|H^C)}{P(E)}}=\frac{P(H)}{P(H^C)}\cdot \frac{P(E|H)}{P(E|H^C)}$$

Quindi possiamo vederlo anche come:

$$\text{Vecchio rapporto }\cdot \frac{P(E|H)}{P(E|H^C)}$$

Il nostro rapporto a favore quindi aumenta se $P(E|H)>P(E|H^C)$ ovvero se il loro rapporto > 1. Aumenta se appunto l’ipotesi è vera piuttosto che quando è falsa.

Bayes Generalizzato

Avevamo visto la probabilità totale generalizzata, possiamo generalizzare anche il teorema di Bayes:

$$P(F_i|E)=\frac{P(F_i)\cdot P(E|F_i)}{\sum _{j=i}^{n}P(F_j)\cdot P(E|F_j)}$$

Esercizio

Un aereo è scomparso, si presume sia finito con uguale probabilità in una di 3 zone $Z_1,Z_2,Z_3$.

Abbiamo:

• $1-{\beta }_i$ = Probabilità di trovare l’aereo in $Z_i$ se è effettivamente in $Z_i$.
• Sapendo che le ricerche in $Z_1$ hanno dato esito negativo, qual è la probabilità che l’aereo sia in $Z_i$ con $i=1,2,3$?
• $R_i=\text{L’aereo eˋ in }{Z}_i$
• $E=\text{La ricerca in }{Z}_1\text{ ha dato esito negativo}$
• $P(R_1)=P(R_2)=P(R_3)=\frac{1}{3}$
• $P(R_i|E)=?$

$$\begin{array}{r}P(R_1|E)=\frac{P(E\cap R_1)}{P(E)}=\frac{P(R_1)\cdot P(E|R_1)}{P(E)}=\frac{P(R_1)\cdot P(E|R_1)}{\sum _{k=1}^{3}P(R_k)\cdot P(E|R_k)}=\frac{\frac{1}{3}\cdot {\beta }_1}{\frac{1}{3}{\beta }_1+\frac{1}{3}\cdot 1+\frac{1}{3}\cdot 1}=\frac{{\beta }_1}{{\beta }_1+2}\end{array}$$

Adesso prendiamo $j=2,3$

$$\begin{array}{r}P(R_j|E)=\frac{P(R_j)\cdot P(E|R_j)}{P(E)}=\frac{\frac{1}{3}\cdot 1}{\frac{1}{3}{\beta }_1+\frac{1}{3}+\frac{1}{3}}=\frac{1}{{\beta }_1+2}\end{array}$$

Proposizione

Sia $F$ evento con $P(F)>0$ allora la funzione $E\to P(E|F)$ al variare di $E$ eventi è una funzione di probabilità. Abbiamo quindi una serie di indentità:

1. $P(E^C|F)=1-P(E|F)$
2. $P(A\cup B|F)=P(A|F)+P(B|F)-P(A\cap B|F)$
3. $A_1,\dots ,A_n$ eventi 2 a 2 disgiunti allora $P\left(\bigcup _{i=1}^n{A}_i|F\right)=\sum _{i=1}^{n}P(A_i|F)$

Dimostrazioni negli appunti non so se le metto =P dato che dobbiamo solo fare esercizi

Esempio: lanciamo 2 dadi e valutiamo la speranza degli eventi con $P$. Sappiamo che “il primo dado ha dato un numero pari” e chiamiamo questo evento $A$ quindi adesso la calcoliamo $P(\cdot ,A)$. Se poi sappiamo che si verifica $B=\text{"Il 2 dato da un numero dispari"}$ allora valutiamo $Q(\cdot ,B)$ dove $Q=P(\cdot ,A)$ ottenendo quindi che $Q=(\cdot ,A\cap B)$.

Indipendenza di Eventi

Due eventi $E$ e $F$ si dicono indipendenti se $P(E\cap F)=P(E)\cdot P(F)$ e si scrive $E\perp \perp F$, sarebbe più intuitivo dire che $E$ ed $F$ sono indipendenti se $P(E|F)=P(E)$ e $P(F|E)=P(F)$ però per dare un senso a $P(E|F)$ è necessario che $P(F)>0$ e analogamente per $P(F|E)$ serve che $P(E)>0$.

Tolto il caso in cui uno tra $E$ ed $F$ abbia probabilità 0, la formulazione intuitiva e la definizione coincidono.

Infatti vale:

$$\begin{array}{r}\text{Sia }F\text{ con }P(F)>0\text{ allora, per ogni evento }E\\ \\ P(E|F)=P(E)\iff P(E\cap F)=P(E)\cdot P(F)\end{array}$$

Dimostrazione

$$\begin{array}{rl}& \text{Sia }P(E|F)=P(E)\text{ allora siccome }P(E|F)=\frac{P(E\cap F)}{P(F)}\text{ abbiamo che }\frac{P(E\cap F)}{P(F)}=P(E)\\ & \\ & \text{Moltiplichiamo per }P(F)\to P(F)\cdot \frac{P(E\cap F)}{P(F)}=P(E)\cdot P(F)\iff P(E\cap F)=P(E)\cdot P(F)\\ & \\ & \text{Quindi supponiamo che }P(E\cap F)=P(E)\cdot P(F)\text{ e dividiamo per }P(F)>0\\ & \\ & \underset{P(E|F)}{\underbrace{\frac{P(E\cap F)}{P(F)}}}=P(E)\end{array}$$

Analogamente possiamo provare che se $P(E)>0$ allora $P(F|E)=P(F)\iff P(E\cap F)=P(E)\cdot P(F)$.

Osservazione

Se $P(E)=0$ allora $E,F$ sono indipendenti per ogni $F$ evento, ovvero esistono eventi con probabilità nulla ma possibili.

Sia $E$ con $P(E)=0$ e sia $F$ evento dobbiamo verificare che $P(E\cap F)=\stackrel{0}{\overbrace{P(E)}}\cap P(F)$.

Quindi dobbiamo provare che $P(E\cap F)=0$, sappiamo che $E\cap F\subset E$ e per monotonia $P(E\cap F)\le P(E)=0$.

Esempio

Lancio due volte un dado $E=\{\text{Il 1° lancio daˋ 4}\},F=\{\text{La somma dei lanci daˋ 6}\}$. $E\perp \perp F$?

$$\begin{array}{rl}& S=\{(a,b):a,b\in \{1,2,3,4,5,6\}\}\text{ esiti equiprobabili}\\ & P(E)=\frac{1}{6}\\ & F=\{(a,b)\in S:a+b=6\}=\{(1,5),(2,4),(3,3),(4,2),(5,1)\}\\ & P(F)=\frac{5}{36}\\ & P(E\cap F)=\{(4,2)\}=\frac{1}{36}\\ & \\ & P(E\cap F)\ne P(E)\cdot P(F)\text{ quindi }E/\perp \perp F\end{array}$$

Esempio

Lancio due volte un dado $E=\{\text{Il 1° lancio daˋ 4}\},F=\{\text{La somma dei lanci daˋ 7}\}$. $E\perp \perp F$?

$$\begin{array}{rl}& S=\{(a,b):a,b\in \{1,2,3,4,5,6\}\}\text{ esiti equiprobabili}\\ & P(E)=\frac{1}{6}\\ & F=\{(a,b)\in S:a+b=6\}=\{(1,6),(2,5),(3,4),(4,3),(5,2),(6,1)\}\\ & P(F)=\frac{6}{36}=\frac{1}{6}\\ & P(E\cap F)=\{(4,3)\}=\frac{1}{36}\\ & \\ & P(E\cap F)=P(E)\cdot P(F)\text{ quindi }E\perp \perp F\end{array}$$

Se ho un esperimento composto da sottoesperimenti che non si influenzano allora eventi riferiti a sottoesperimenti diversi risultano indipendenti.

Esempio

Lancio due volte un dado e ho due sottoesperimenti: primo e secondo lancio. I due sottoesperimenti non si possono influenzare.

$E=\text{1° daˋ pari},F=\text{2° daˋ multiplo di 3}$, trattandosi di eventi che si riferiscono a lanci diversi ci aspettiamo che siano indipendenti, verifichiamo che $P(E\cap F)=P(E)\cdot P(F)$.

$$\begin{array}{rl}& S=\{(a,b):a,b\in \{1,2,3,4,5,6\}\}\text{ esiti equiprobabili}\\ & P(E)=\frac{3}{6}=\frac{1}{2}\\ & P(F)=\frac{2}{6}=\frac{1}{3}\\ & E\cap F=\{(a,b):a\in \{2,4,6\},b\in \{3,6\}\}\\ & P(E\cap F)=\frac{|E\cap F|}{|S|}=\frac{6}{36}=\frac{1}{6}\text{ che eˋ uguale a }\frac{1}{2}\cdot \frac{1}{3}\text{ quindi }E\perp \perp F\end{array}$$

Proposizione: Dati $E,F$ eventi, $E\perp \perp F\Rightarrow E^C\perp \perp F$

Dimostrazione

Supponiamo $E\perp \perp F$ e quindi $P(E\cap F)=P(E)\cdot P(F)$, dobbiamo provare che $E^C\perp \perp F$, cioè $P(E^C\cap F)=P(E^C)\cdot P(F)$.

$$\begin{array}{rl}\text{Abbiamo che }P(E^C)=1-P(E)& \\ & \\ P(E^C\cap F)=(1-P(E))\cdot P(F)& =P(F)-\underset{E\perp \perp F\Rightarrow P(E)\cdot P(F)}{\underbrace{P(E\cap F)}}\\ & =P(F)-P(E)\cdot P(F)\\ \text{ Raggruppando }P(F)\to & =P(F)\cdot (1-P(E))\\ & =P(F)\cdot P(E^C)\end{array}$$

Supponiamo adesso di avere tre, eventi $E,F,G$: sappiamo che $E,F$ sono indipendenti e anche $E,G$ sono indipendenti. Possiamo dire che $E$ è indipendente da $F\cap G$? No, possono essere dipendenti.

Esempio

Lancio 2 dadi e definisco gli eventi:

$$\begin{array}{rl}& E=\text{La somma dei dadi daˋ 7}\\ & F=\text{Il primo dado daˋ 4}G=\text{Il secondo dado daˋ 3}\end{array}$$

Prendendo gli esempi precedenti sappiamo che $E\perp \perp F$, quindi dobbiamo provare che $E\perp \perp G$:

$$\begin{array}{rl}& P(E)=\frac{6}{36}=\frac{1}{6}\\ & P(G)=\frac{1}{6}\\ & P(E\cap G)=\frac{1}{36}\\ & \text{Abbiamo che }P(E)\cdot P(G)=\frac{1}{6}\cdot \frac{1}{6}=\frac{1}{36}=P(E\cap G)\\ & \text{Quindi abbiamo mostrato che }E\perp \perp G\\ & \\ & \text{Notiamo peroˋ che }E\cancel{\perp \perp }(F\cap G)\text{ infatti }P(E|F\cap G)=1\ne P(E)\end{array}$$

Definizione

Dati 3 eventi $E,F,G$ si dice che sono indipendenti se:

$$\begin{array}{rl}& P(E\cap F)=P(E)\cdot P(F)\to E\perp \perp F\\ & P(E\cap G)=P(E)\cdot P(G)\to E\perp \perp G\\ & P(F\cap G)=P(F)\cdot P(G)\to F\perp \perp G\\ & P(E\cap F\cap G)=P(E)\cdot P(F)\cdot P(G)\end{array}$$

Teorema

Se $E,F,G$ sono indipendenti, allora $E$ è indipendente da ogni evento costruito a partire da $F$ e $G$ usando unione, intersezione e complementare.

Quindi, ad esempio:

Se $E,F,G$ sono indipendenti, allora:

$$\begin{array}{rl}& E\perp \perp (F\cap G)\\ & E\perp \perp (F\cup G)\\ & E\perp \perp (F^C\cup G)\\ & E\perp \perp F^C\\ & ecc\dots \end{array}$$

E se ho più di 3 eventi?

Definizione

Dati $n$ eventi $E_1,\dots ,E_n$ questi sono detti indipendenti se $\forall A\subset \{1,2,\dots ,n\}$ con $A\ne \varnothing$ vale:

$$P\left(\bigcap _{i\in A}{E}_i\right)=\prod _{i\in A}P(E_i)$$

Questa formula è interessante per $A$ tale che $|A|\ge 2$ infatti se $A=\{i_0\}$ allora diventa $P(E_{i_0})=P(E_{i_0})$ che è banalmente vero.

Esempio

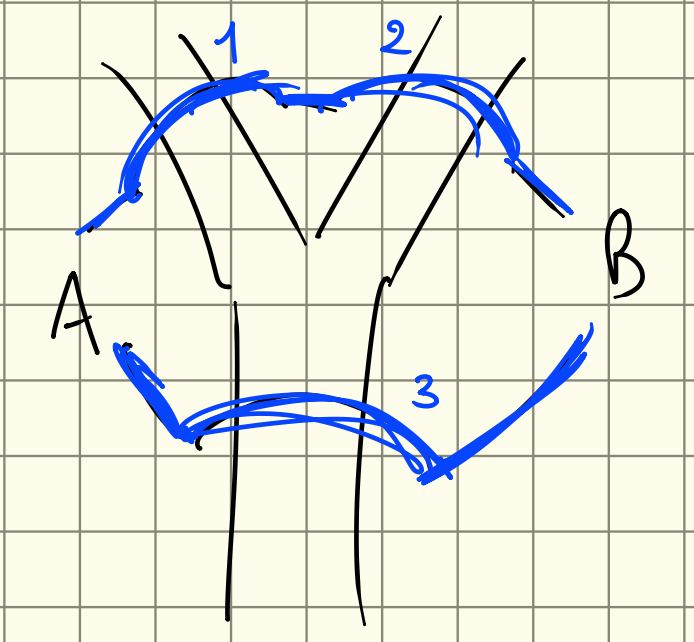
Prendiamo questi ponti, ogni ponte è integro con probabilità $p$ (e quindi distrutto con probabilità $1-p$), indipendentemente da ponte a ponte. Supponiamo $p=0.3$

Calcolare $P(\text{Partendo da A arrivo B})$.

Definiamo l’evento $E_i=\text{Il ponte i eˋ integro}$.

Le strade che posso percorrere sono date da $(E_1\cap E_2)\cup E_3$, quindi:

$$\begin{array}{rl}P(A\to B)& =P((E_1\cap E_2)\cup E_3)\\ & =P(E_1\cap E_2)+P(E_3)-P(E_1\cap E_2\cap E_3)\\ & =P(E_1)\cdot P(E_2)+P(E_3)-P(E_1)\cdot P(E_2)\cdot P(E_3)\\ & =p^2+p-p^3=(0.3{)}^2+0.3-(0.3{)}^3\end{array}$$

Oppure possiamo calcolare

$$\begin{array}{r}1-\underset{E_3^C\cap (E_1^C\cup E_2^C)}{\underbrace{P(\text{Da A non arrivo B})}}=\stackrel{\text{3 rotto e almeno 1 o 2 rotto}}{\overbrace{P(E_3^C\cap (E_1^C\cup E_2^C))U}}=\text{Da finire :(}\end{array}$$

---

Problema Monty Hall

Siamo in un gioco dove dobbiamo scegliere 1 fra 3 porte, in una di queste è presente una macchina mentre nelle altre due abbiamo delle pecore, dopo che scegliamo una porta il conduttore ci apre un’altra porta che contiene una pecora e ci propone uno scambia, conviene accettarlo o no?

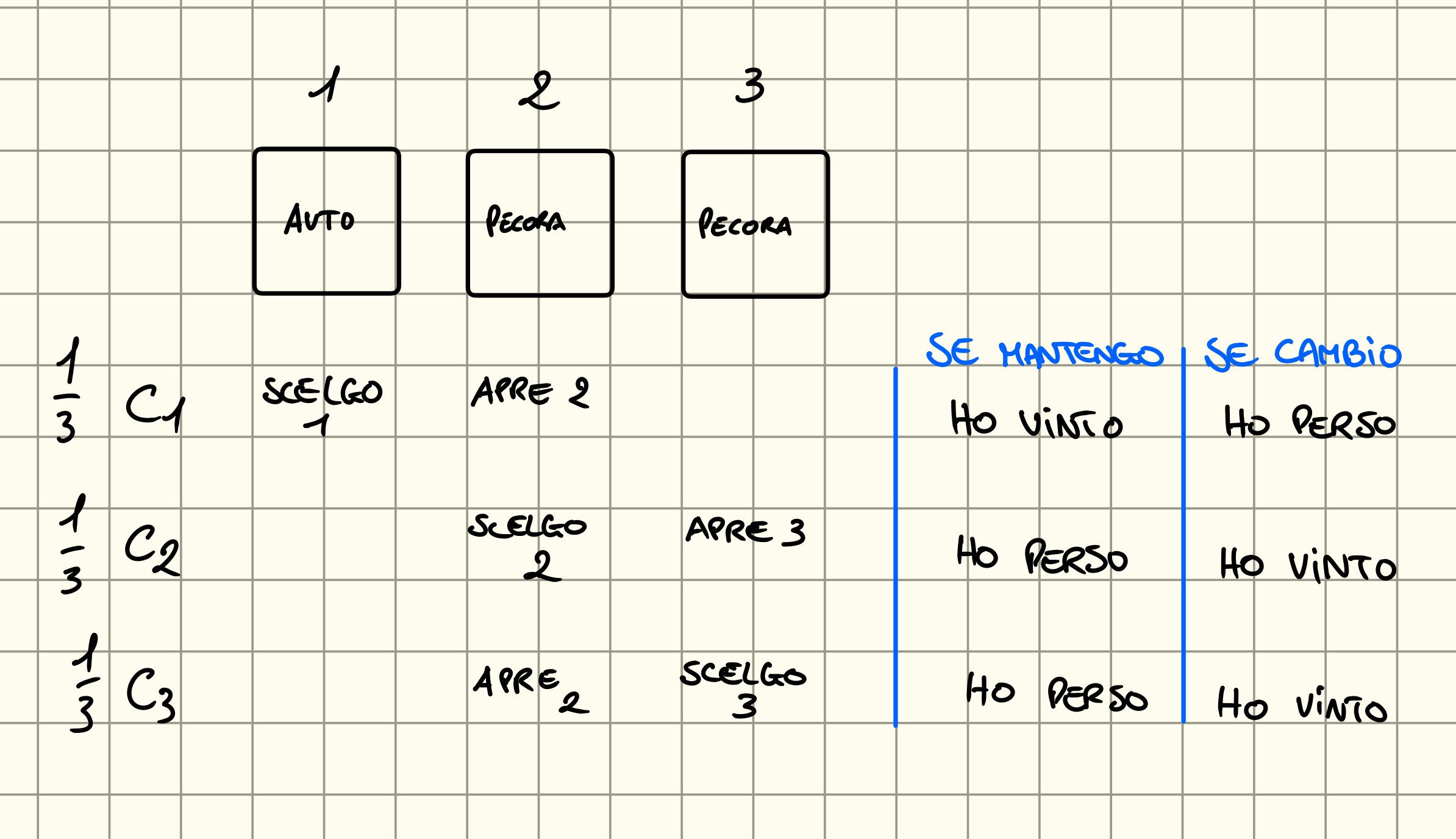
Quindi se cambiamo abbiamo una possibilità di vittoria di $\frac{2}{3}$ mentre se manteniamo la nostra scelta di $\frac{1}{3}$.

---

Tornando agli eventi indipendenti

Esempio

Siano $A,B,C,D$ eventi indipendenti con $P(A)=0.2,P(B)=0.5,P(C)=0.7,P(D)=0.1$ calcolare $P(A\cap C),P(B\cap C\cap D),P(B\cup C)$.

$$\begin{array}{rl}& P(A\cap C)=P(A)\cdot P(C)=0.2\cdot 0.7=0.14\\ & P(B\cap C\cap D)=P(B)\cdot P(C)\cdot P(D)=0.5\cdot 0.7\cdot 0.1=0.035\\ & P(B\cup C)=P(B)+P(C)-P(B\cap C)=0.5+0.7-(0.5\cdot 0.7)=0.85\\ & \\ & \text{In alternativa:}\\ & \\ & P(B\cup C)=1-P((B\cup C{)}^C)=1-P(B^C\cap C^C)=1-P(B^C)\cdot P(C^C)\\ & =1-(1-0.5)\cdot (1-0.7)=0.85\end{array}$$

Esempio con percorsi

Se prendiamo come esempio un circuito con componenti in parallelo ci basta che un solo componente funzioni per permettere il passaggio di corrente, mettiamo caso che ogni componente è indipendente dalle altre e che $p_i=P(\text{La componente i eˋ funzionante})$, come si calcola $P(\text{Il sistema funziona})$?

$$\begin{array}{rl}& P\left(\bigcup _{i=1}^n{E}_i\right)\text{ con }{E}_i=\text{"La componente funziona"}\\ & P\left(\bigcup _{i=1}^n{E}_i\right)=1-\left(P{\left(\bigcup _{i=1}^n{E}_i\right)}^C\right)=1-P\left(\bigcap _{i=1}^n{E}_i^C\right)\\ & =1-\prod _{i=1}^{n}P(E_i^C)=1-\prod _{i=1}^n(1-p_i)\end{array}$$

Variabili Aleatorie

Reali

Dato uno spazio di probabilità $(S,P)$, una variabile aleatoria è una funzione $X:S\to \mathbb{R}$ quindi una funzione che mappa elementi dello spazio campionari in numeri reali.

Esempio

Lancio una moneta due volte abbiamo $X:=\#\text{volte in cui esce testa}$, $X$ è una variabile aleatoria.

Abbiamo $S=\{(T,T),(C,C),(T,C),(C,T)\}$ e sono tutti esiti equiprobabili, abbiamo:

$X((T,T))=2,X((T,C))=1,X((C,T))=1,X((C,C))=0$

Esempio

Lancio due volte un dado e abbiamo $X:=\#\text{Somma dei numeri usciti}$, otteniamo quindi

$S=\{(a,b):a,b\in \{1,2,3,4,5,6\}\}$ e quindi abbiamo esiti equiprobabili.

$X((a,b))=a+b$ quindi ad esempio $X((1,5))=6$

Discrete

Una variabile aleatorie $X$ è detta discreta se i valori che può assumere $\{X_i{\}}_{i\in I}$ formano un insieme finito o infinito numerabile. Quindi ad esempio la variabile aleatori degli esempi sopra è discreta.

Densità di probabilità discreta

Data $X$ variabile aleatoria che assume $\{X_i{\}}_{i\in I}$, la densità di probabilità discreta di $X$ è la funzione:

$$P_X:\{X_i{\}}_{i\in I}\to [0,1],P_X:=P(X=X_i)$$

È quindi una funzione che descrive la probabilità associata a ciascun valore possibile di una variabile aleatoria discreta.

Esempio

Lancio due volte una moneta e v.a. $X:=\#\text{Teste Uscite}$ quindi $X(T,T)=2,X(T,C)=X(C,T)=1,X(C,C)=0$.

Quindi $X$ è una variabile aleatoria che assume i valori 0,1,2.

$p_X:\{0,1,2\}\to [0,1]$ e $P_X(a)=P(X=a)$, quindi calcoliamo:

$P_X(0)=P(X=0)=\frac{1}{4}$ poi $P_X(1)=P(X=1)=\frac{2}{4}$ e $P_X(2)=P(X=2)=\frac{1}{4}$

Esempio

Lancio due volte un dado e la variabile aleatoria è $X:=\#\text{Somma dei valori usciti}$.

Quindi abbiamo esiti equiprobabili in $S=\{(a,b):a,b\in \{1,2,3,4,5,6\}\}$.

$X(a,b)=a+b$ assume i valori $\{2,3,\dots ,12\}$ e calcoliamo:

$$\begin{array}{rl}& PX(2)=P(X=2)=P(\{(1,1)\})=\frac{1}{36}\\ & PX(3)=P(X=3)=P(\{(1,2),(2,1)\})=\frac{2}{36}\\ & \text{In generale }{P}_X(k)=\{\begin{array}{l}\frac{k-1}{36}\text{ k=2,3,4,5,6,7}\\ \frac{13-k}{36}\text{ k=7,8,9,10,11,12}\end{array}\end{array}$$

---

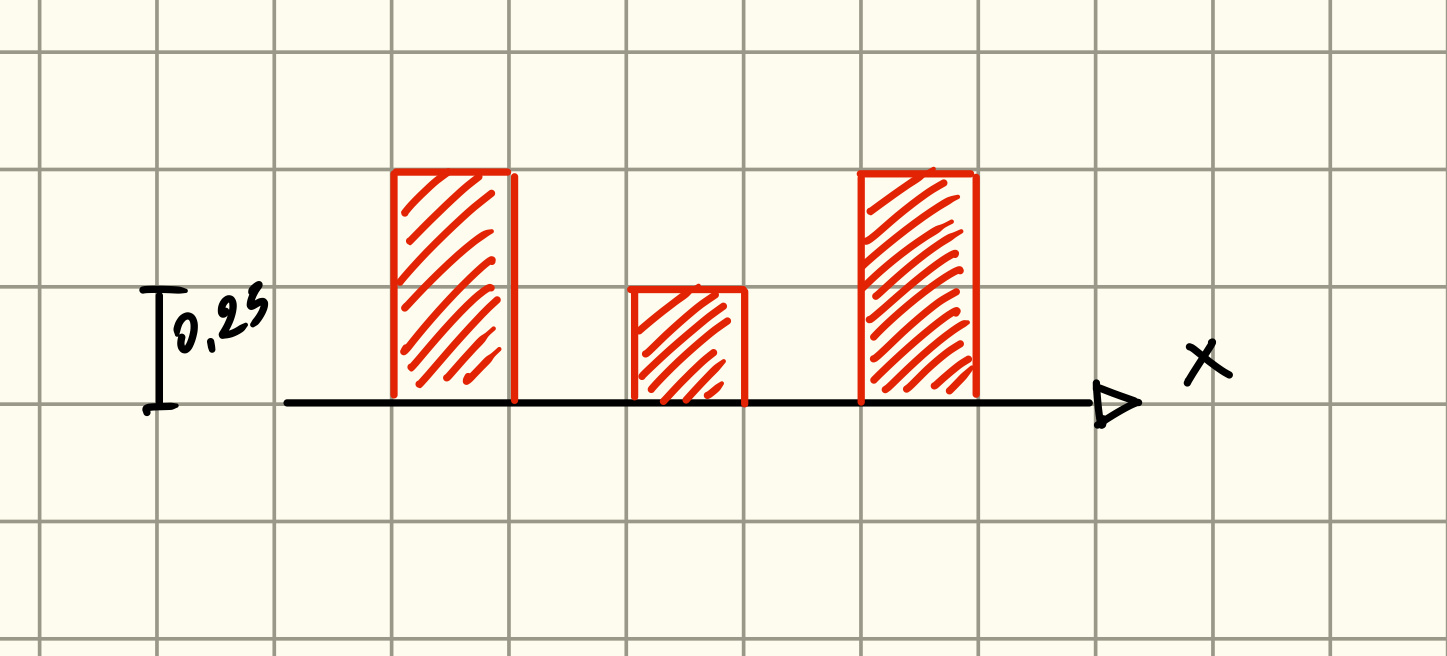
Possiamo rappresentare la densità di probabilità discreta con un istogramma.

Ad esempio sia $X$ il numero di teste nel lancio di due monete, sappiamo che:

$P_X(0)=\frac{1}{4},P_X(1)=\frac{2}{4},P_X(2)=\frac{1}{4}$

Valore Atteso

Data una variabile aleatorie discreta $X$ che assume valore $\{X_i{\}}_{i\in I}$, definiamo il valore atteso di $X$ come:

$$E[X]=\sum _{i\in I}{X}_{i}P(X=X_i)=\sum _{i\in I}{X}_i{P}_X(X_i)$$

Dove $E$ indica expected value of X.

Esempio

Lanciamo una moneta 2 volte e come variabile aleatoria abbiamo $X=\#\text{Teste Uscite}$.

$$E[X]=0\cdot \frac{1}{4}+1\cdot \frac{2}{4}+2\cdot \frac{1}{4}=1$$

Esercizio

Data un’urna con 3N e 2B. Estraggo due palline senza rimpiazzo, sia $X:=\#\text{Palline nere estratte, calcolare}$ calcolare $E[X]$.

Abbiamo $X=\{0,1,2\}$

• $P(X=0)=\frac{2\cdot 1}{5\cdot 4}=\frac{2}{20}$
• $P(X=1)=\frac{3\cdot 2}{5\cdot 4}+\frac{2\cdot 3}{5\cdot 4}=\frac{12}{20}$
• $P(X=2)=\frac{3\cdot 2}{5\cdot 4}=\frac{6}{20}$

$$E[X]=0\cdot \frac{2}{20}+1\cdot \frac{12}{20}+2\cdot \frac{6}{20}=\frac{6}{5}$$

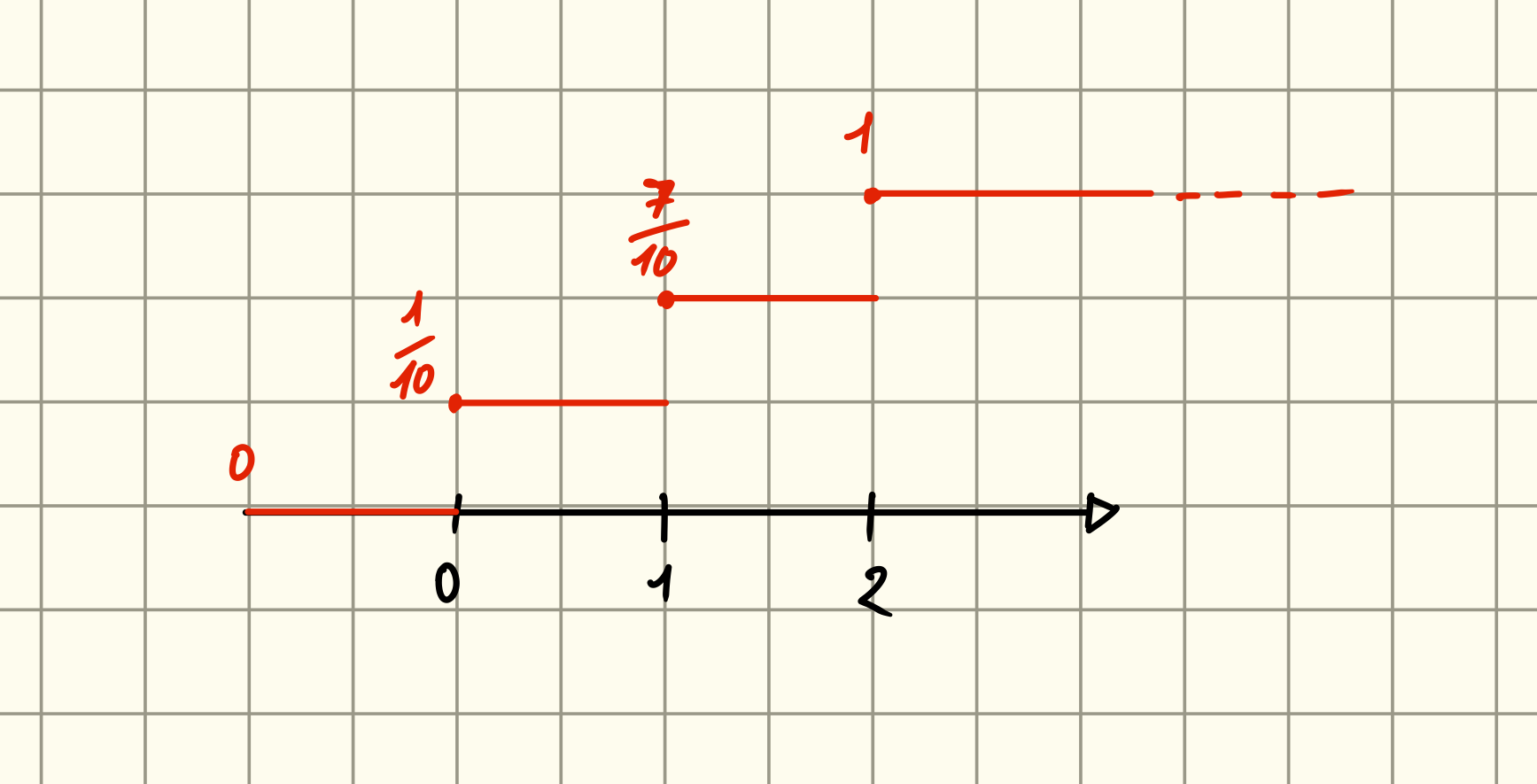
Funzione di Distribuzione (o Ripartizione)

Data una variabile aleatoria $X$, la sua funzione di distribuzione è definita come:

$$F_X:\mathbb{R}\to [0,1]\text{ con }{F}_X(a)=P(X\le a)\forall a\in \mathbb{R}$$

Esempio

Sia $X$ la stessa v.a. di prima determiniamo $F_X$.

• Se $a<0$ allora $F_X(a)=P(X\le a)=0$
• Se $0\le a<1$ allora $F_X(a)=P(X\le a)=\frac{1}{10}$
• Se $1\le a<2$ allora $F_X(a)=P(X\le a)=F_X(\{X=1\cup \{X=0\})=\frac{1}{10}+\frac{6}{10}=\frac{7}{10}$
• Se $a\ge 2$ allora $F_X(a)=P(X\le a)=F_X(\{X=0\}\cup \{X=1\}\cup \{X=\})=\frac{1}{10}+\frac{6}{10}+\frac{3}{10}=1$

Quindi guardando meglio la funzione abbiamo che:

$$F_X(a)=\{\begin{array}{l}0sea<0\\ \frac{1}{10}se0\le a<1\\ \frac{7}{10}se1\le a<2\\ 1sea\ge 2\end{array}$$

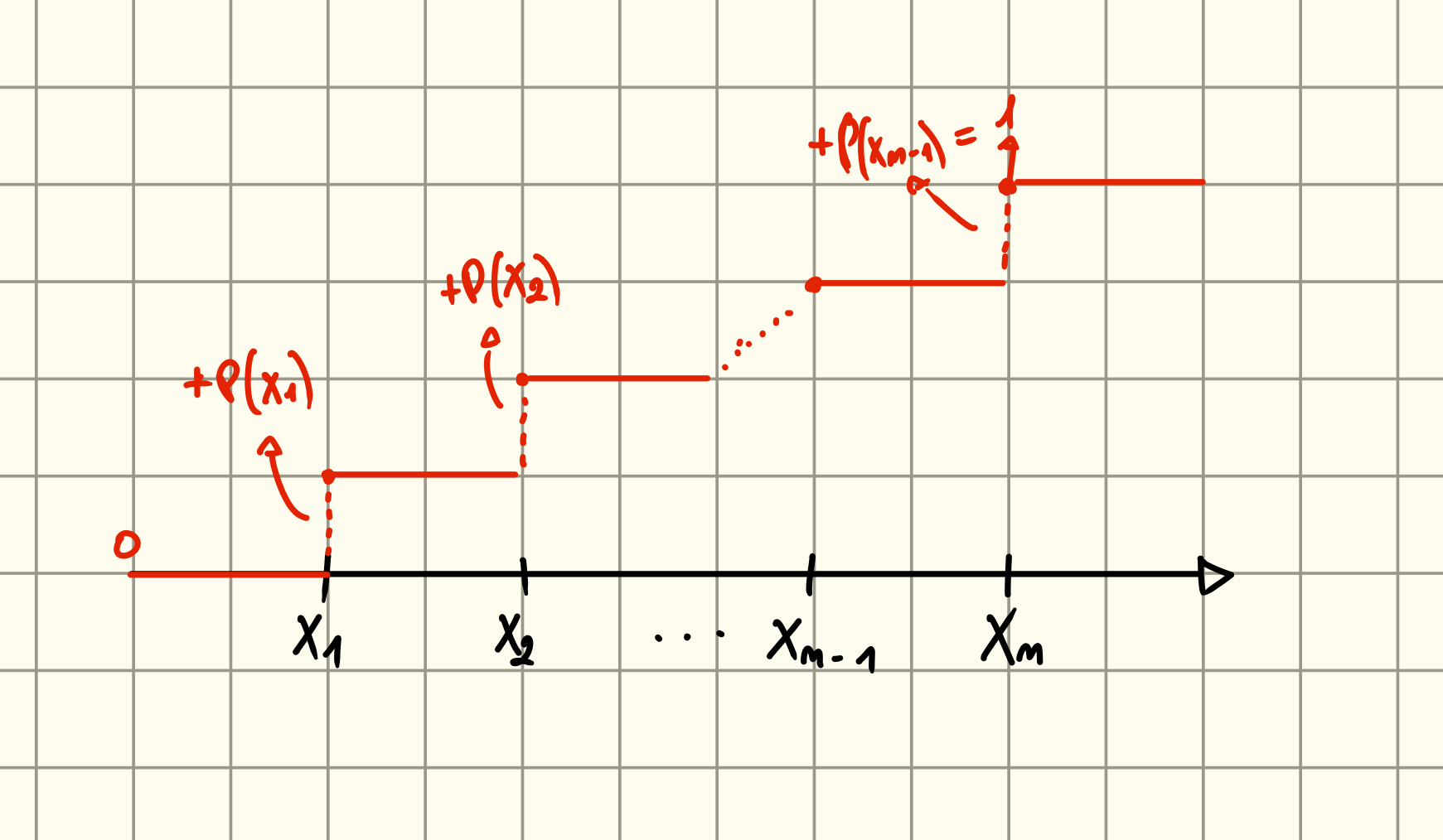
In generale se $X$ è variabile aleatoria che assume $n$ valori dati da $X_1\le X_2\le \cdots \le X_n$ allora si ha che:

$$F_X(a)=\{\begin{array}{l}0sea<X_1\\ P(X_1)se{X}_1\le a<X_2\\ P(X_1)+P(X_2)se{X}_2\le a<X_3\\ .\\ P(X_1)+P(X_2)+\cdots +P(X_k)se{X}_k\le a<X_{k+1}\\ .\\ 1=P(X_1)+\cdots +P(X_n)sea\ge X_n\end{array}$$

E vista come grafico:

Esercizio

Estraggo 3 carte da un mazzo da 40. Sia $X:=\#\text{Carte di bastoni uscite}$ determinare $P_X,F_X,E[X]$

• $P(X=0)=\frac{\left(\genfrac{}{}{0ex}{}{30}{3}\right)}{\left(\genfrac{}{}{0ex}{}{40}{3}\right)}=\frac{812}{1976}$
• $P(X=1)=\frac{\left(\genfrac{}{}{0ex}{}{30}{2}\right)\left(\genfrac{}{}{0ex}{}{10}{1}\right)}{\left(\genfrac{}{}{0ex}{}{40}{3}\right)}=\frac{870}{1976}$
• $P(X=2)=\frac{\left(\genfrac{}{}{0ex}{}{30}{1}\right)\left(\genfrac{}{}{0ex}{}{10}{2}\right)}{\left(\genfrac{}{}{0ex}{}{40}{3}\right)}=\frac{270}{1976}$
• $P(X=3)=\frac{\left(\genfrac{}{}{0ex}{}{10}{3}\right)}{\left(\genfrac{}{}{0ex}{}{40}{3}\right)}=\frac{24}{1976}$

Quindi abbiamo:

$$E[X]=0\cdot \frac{812}{1976}+1\cdot \frac{870}{1976}+2\cdot \frac{270}{1976}+3\cdot \frac{24}{1976}=\frac{1482}{1976}$$

E per $F(a)$:

$$F_X(a)=\{\begin{array}{l}0sea<0\\ \frac{812}{1976}se0\le a<1\\ \frac{812}{1976}+\frac{870}{1976}se1\le a<2\\ \frac{812}{1976}+\frac{870}{1976}+\frac{270}{1976}se2\le a<3\\ 1sea\ge 3\end{array}$$

Varianza di una variabile aleatoria

Sia $X$ una v.a. discreta, la varianza di $X$ è definita come $Var(X):=E[(X-\underset{\text{valore atteso}}{\underbrace{EX}}{)}^2]$.

La varianza torna utile perché quantifica quanto la v.a. $X$ si discosta dal suo valore atteso.

Esempio

Sia $X$ una v.a. con $X(1)=\frac{1}{2}$ e $X(-1)=\frac{1}{2}$ abbiamo che:

$$E[X]=EX=1\cdot \frac{1}{2}+-1\cdot \frac{1}{2}=0$$

e quindi:

$$Var(X)=E[(X-EX{)}^2]=E[(X-0{)}^2]=E[X^2]=1$$

Esempio

Sia $X$ una v.a. che assume i valore $\{-3,0,1,2\}$ con:

• $P_X(-3)=\frac{2}{10}$
• $P_X(0)=\frac{1}{10}$
• $P_X(1)=\frac{4}{10}$
• $P_X(2)=\frac{3}{10}$

Calcolare $EX$ e $Var(X)$.

• $EX=-3\cdot \frac{2}{10}+0\cdot \frac{1}{10}+1\cdot \frac{4}{10}+2\cdot \frac{3}{10}=\frac{4}{10}$

$$Var(X)=E\left[{\left(X-\frac{4}{10}\right)}^2\right]$$

Ma come calcoliamo ${\left(X-\frac{4}{10}\right)}^2$? Dobbiamo vedere i singoli casi

• $X=-3\to (X-0.4{)}^2=(-3-0.4{)}^2=11.56$
• $X=0\to (X-0.4{)}^2=(-0-0.4{)}^2=0.16$
• $X=1\to (X-0.4{)}^2=(1-0.4{)}^2=0.36$
• $X=2\to (X-0.4{)}^2=(2-0.4{)}^2=2.56$

Quindi otteniamo:

$$(X-0.4{)}^2=\{\begin{array}{l}11.56\text{ con probabilitaˋ }\frac{2}{10}\\ 0.16\text{ con probabilitaˋ }\frac{1}{10}\\ 0.36\text{ con probabilitaˋ }\frac{4}{10}\\ 2.56\text{ con probabilitaˋ }\frac{3}{10}\end{array}$$

E quindi:

$$Var(X)=E[(X-0.4{)}^2]=11.56\cdot 0.2+0.16\cdot 0.1+0.36\cdot 0.4+2.56\cdot 0.3=3.24$$

Non linearità della Varianza

Non è lineare infatti $Var(aX+b)=a^{2}Var(X)$

Dimostrazione

$$\begin{array}{rl}Var(aX+b)& =E[((aX+b)-E[aX+b]{)}^2]\\ \text{Linearitaˋ di E }& =E[(aX+\cancel{b}-aEX-\cancel{b}{)}^2]\\ \text{Raccogliamo }& =E[a^2(X-EX{)}^2]\\ \text{Linearitaˋ di E }& =a^2\underset{\text{Definizione Varianza}}{\underbrace{E[(X-EX{)}^2]}}=a^{2}Var(X)\end{array}$$

Quindi abbiamo anche che:

$${\sigma }_{aX+b}=\sqrt{Var(aX+b)}=|a|\sqrt{Var(X)}=|a|{\sigma }_X$$

Deviazione Quadrata sotto

Deviazione Quadrata

Sia $X$ una v.a., la deviazione quadrata standard di $X$ è data da ${\sigma }_X:=\sqrt{Var(X)}$

---

Dati $(S,P)$ e $X:S\to \mathbb{R}$

Sia $f:\mathbb{R}\to \mathbb{R}$. Denoto con $f(X)$ la variabile aleatoria $f\circ X$, abbiamo quindi che:

$$\underset{f\circ X=f(X)}{\underbrace{S\stackrel{X}{\to }\mathbb{R}\stackrel{f}{\to }\mathbb{R}}}$$

• $f(X):S\to \mathbb{R}$ è una variabile aleatoria discreta

Infatti:

• $X:S\to \mathbb{R}$ assume valori $\{X_i:i\in I\}$
• $f(X)=f\circ X:S\to \mathbb{R}$ assume valori $\{f(X_i):i\in I\}$

Esempio

Lancio 10 volte una moneta e $X=\#\text{Teste Uscite}$. Vinco 2 Euro per ogni testa e perdo 1 euro per ogni croce.

$Y=\#\text{Guadagno Algebrico}$, posso esprimere $Y$ come $f(X)$.

$$Y=2\cdot X-1(10-X)=3X-10Y=f(X)\text{ dove }f:\mathbb{R}\to \mathbb{R}$$

---

Ho $(S,P)$ e $X:S\to \mathbb{R}$ v.a.

Ho $f:\mathbb{R}\to \mathbb{R}$, se $X$ è una v.a. discreta, allora $f\circ X=f(X)$ è v.a. discreta.

Ci interessa calcolare $E[f(X)]$

Primo Metodo

Determino i possibili valori di $f(X)$ che chiamo $\{y_j:j\in J\}$ e calcolo $P(f(X)=y_j)\forall j\in J$. Quindi per definizione:

$$E[f(X)]=\sum _j{y}_j\cdot P(f(X)=y_j)$$

Secondo Metodo Teorema

Sia $X$ v.a. discreta che assume valori $\{X_i{\}}_{i\in I}$ e sia $f:\mathbb{R}\to \mathbb{R}$. Allora:

$$E[f(X)]=\sum _{i\in I}f(X_i)\cdot P(X=X_i)=\sum _{i\in I}f(X_i)\cdot P_X(X_i)$$

Dimostrazione

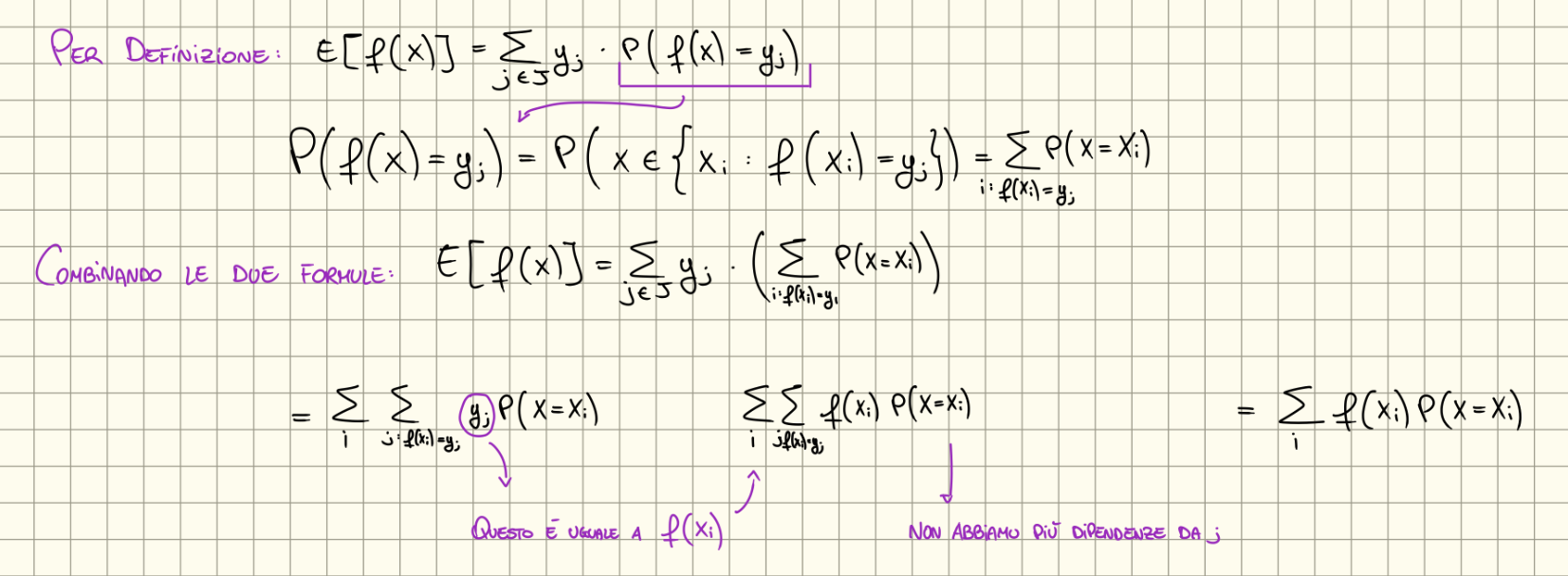
Esempio

Data $X$ che assume valori $-1,0,3$ con prob $0.2,0.5,0.3$ rispettivamente. Calcolare $E((X-1{)}^2)$.

Primo Metodo

$$Y=(X-1{)}^2\text{ assume valori }\{\begin{array}{l}4\text{ se }X=-1oX=3\\ 1\text{ se }X=0\end{array}$$

• $P(Y=4)=P(X=-1)+P(X=3)=0.2+0.3=0.5$
• $P(Y=1)=P(X=0)=0.5$
• $E[Y]=4\cdot 0.5+1\cdot 0.5=2.5$

Secondo Metodo

$$\begin{array}{rl}E[Y]& =f(-1)\cdot P(X=-1)+f(0)\cdot P(X=0)+f(3)\cdot P(X=3)\\ & =(-1-1{)}^2\cdot 0.2+(0-1{)}^2\cdot 0.5+(3-1{)}^2\cdot 0.3\\ & =0.8+0.5+1.2=2.5\end{array}$$

---

Valore atteso con funzione

Se $X$ è v.a. discreta che assume i valori $\{x_i{\}}_{i\in I}$ e $f:\mathbb{R}\to \mathbb{R}$ allora:

$$E[f(X)]=\sum _{i\in I}f(x_i)\cdot P(X=x_i)\text{La chiamiamo *}$$

Esempio

$X$ assume valori $\{-1,0,2,3\}$ e abbiamo che:

• $P(-1)=0.1$
• $P(0)=0.2$
• $P(2)=0.2$
• $P(3)=0.5$

Allora:

$$E[(X-1{)}^4]=E[f(X)]\text{ dove }f(u)=(u-1{)}^4$$

Calcoliamolo:

$$E[(X-1{)}^4]=E[f(X)]=f(-1)P(-1)+f(0)P(0)+f(2)P(2)+f(3)P(3)=$$ $$=(-1-1{)}^4\cdot 0.1+(-1{)}^4\cdot 0.2+(2-1{)}^4\cdot 0.2+(3-1{)}^4\cdot 0.5=2$$

Linearità del valore atteso

Sia $X$ v.a. discreta e siano $a,b\in \mathbb{R}$ allora $E[aX+b]=aE[X]+b$

Dimostrazione

Sia $\{x_i{\}}_{i\in I}$ l’insieme dei valori assunti da $X$, inoltre abbiamo che $aX+b=f(X)$ dove $f(u)=au+b$, la scriviamo quindi come funzione di X.

$$\begin{array}{rl}E[aX+b]=E[f(X)]\stackrel{\text{usando *}}{=}\sum _{i\in I}f(x_i)P(X=x_i)& =\sum _{i\in I}(a{x}_i+b)P(X=x_i)\\ & \\ \text{Proprietaˋ Distributiva }& =\sum _{i}a{x}_{i}P(x_i)+bP(x_i)\\ & \\ \text{Portiamo fuori a,b e spezziamo}& =a\underset{E[X]}{\underbrace{\sum _i{x}_{i}P(x_i)}}+b\underset{1}{\underbrace{\sum P(x_i)}}=aE[X]+b\end{array}$$

Esempio

$E[X]=1000$ come calcoliamo $E[3X-500]$ ?

Applichiamo la formula → $E[3X-500]=3E[X]-500=3000-500=2500$

Proposizione

Ricordando che la varianza si calcola $Var(X):=E[(X-EX{)}^2]$, possiamo anche calcolarla come:

$$Var(X)=E[X^2]-(EX{)}^2$$

Dimostrazione

$$\begin{array}{rl}Var(X)=E[(X-EX{)}^2]& =E[f(X)]\text{ dove }f(u)=(u-EX{)}^2\\ \text{Per teorema * }E[f(X)]& =\sum _{i}f(x_i)P(x_i)=\sum _i(x_i-EX{)}^{2}P(x_i)\\ & =\sum _i(x_i^2-2x_{i}EX+(EX{)}^2)P(x_i)\\ & =\underset{E[X^2]\text{ per *}}{\underbrace{\sum _i{x}_i^{2}P(x_i)}}-\underset{-2EX\cdot EX}{\underbrace{2EX\sum _i{x}_{i}P(x_i)}}+\underset{(EX{)}^2}{\underbrace{(EX{)}^2\sum _{i}P(x_i)}}\\ & =E[X^2]-2(EX{)}^2+(EX{)}^2=E[X^2]-(EX{)}^2\end{array}$$

Esempio

$X$ assume valori $\{-1,0,2,3\}$ e abbiamo che:

• $P(-1)=0.1$

• $P(0)=0.2$

• $P(2)=0.2$

• $P(3)=0.5$

  $EX=-1\cdot 0.1+0\cdot 0.2+2\cdot 0.2+3\cdot 0.5=1.8$

  $Var(X)=E[X^2]-(EX{)}^2$

  Calcoliamo $E[X^2]=(-1{)}^{2}P(-1)+(0{)}^{2}P(0)+2^{2}P(2)+3^{2}P(3)=5.4$

  E quindi $Var(X)=5.4-(1.8{)}^2=2.16$

  Usando l’altra formula:

  $Var(X)=E((X-EX{)}^2)=(-1-1.8{)}^{2}P(-1)+(0-1.8{)}^{2}P(0)+(2-1.8{)}^{2}P(2)+(3-1.8{)}^{2}P(3)$

---

Ricordiamo la deviazione quadratica standard.

$$=\sqrt{Var(X)}$$

Osserviamo che $Var(X)$ deve essere sempre $\ge 0$ infatti $Var(X)=E[(X-EX{)}^2]$ che è si un numero qualsiasi ma elevato al quadrato e quindi o 0 o positivo.

$$Var(X)=0\iff P(X=EX)=1$$

Se la varianza è uguale a 0 significa che la variabile è costante infatti $Var(X)$ misura quando $X$ si sposta dal suo valore atteso $E[X]$.

Osservazione

Nè la varianza nè la deviazione quadratica sono lineari infatti:

Proprietà

Data $X$ v.a. discreta e dati $a,b\in \mathbb{R}$ vale:

$$Var(aX+b)=a^{2}Var(X)$$

E quindi notiamo che amplifica le costanti moltiplicative e annulla quelle additive.

Esempio

Consideriamo 100 lavoratori di cui 80 hanno salario 500, 10 hanno 1000 e 10 hanno 5000. Scegliamo un lavoratore a caso e indichiamo con $X$ il suo salario. Determinare $E[X],Var(X),\sigma (X)$.

Abbiamo che $X$ può assumere (500,1000,5000) con:

• $P(500)=0.8$
• $P(1000)=0.1$
• $P(5000)=0.1$

$E[X]=500\cdot 0.8+1000\cdot 0.1+5000\cdot 0.1=1000$

$Var(X)=E[(X-EX{)}^2]=E[(X-1000{)}^2]=(500-1000{)}^{2}P(500)+(1000-1000{)}^{2}P(1000)+(5000-1000)P(5000)=1800000$

$\sigma (X)=\sqrt{1800000}=1341.64$

Variabile di Bernoulli

Una v.a. $X$ è detta di Bernoulli di parametro $p\in [0,1]$ se $P(X=1)=p$ e $P(X=0)=1-p$, quindi questa può assumere soltanto due valori.

Quindi in questo caso notiamo che:

$$E[X]=1\cdot P(X=1)+0\cdot P(X=0)=1\cdot p+0\cdot (1-p)=p$$

Mentre

$$Var(X)=E[X^2]-(EX{)}^2=p-p^2=p\cdot (1-p)$$

Dove

$$E[X^2]=1^2\cdot P(X=1)+0^2\cdot P(X=0)=p$$

Variabile Aleatoria Binomiale

Dato un esperimento con $n$ prove indipendenti, tutte svolte nello stesso modo, supponiamo che ogni prova abbiamo due esiti possibili che chiamiamo successo e insuccesso.

Esempi

Lancio una moneta 10 volte, i 10 lanci solo le prove e come successo stabilisco che deve uscire testa.

Lancio un dado 8 volte, gli 8 lanci sono le prove e come successo stabilisco quando esce un numero multiplo di 3.

Definiamo $X=\#\text{Successi Ottenuti}$ nelle prove, notiamo quindi che può assumere come valore, tutti i valori interi da $0$ a $n$, ma con che probabilità?

Chiamiamo $p$ la probabilità che una singola prova ci dia successo come esito.

Proposizione

$$\forall k=0,1,2,\dots ,n\text{ vale }P(X=k)=\left(\genfrac{}{}{0ex}{}{n}{k}\right)\cdot p^k\cdot (1-p{)}^{n-k}$$

Prendiamo l’esempio 2 quindi abbiamo $n=8,p=\frac{1}{3}$ e calcoliamo la probabilità di due successi:

$$P(X=2)=\left(\genfrac{}{}{0ex}{}{8}{2}\right)\cdot {\left(\frac{1}{3}\right)}^2\cdot {\left(\frac{2}{3}\right)}^6$$

Perché vale questa proposizione?

Supponiamo di avere 4 prove e ci chiediamo $P(X=2)$, questo evento $\{X=2\}$ possiamo vederlo come unione di varie prove:

$$E_{SSII}\cup E_{SISI}\cup E_{SIIS}\cup E_{ISSI}\cup E_{IISS}\cup E_{ISSI}$$

Dove i pedici indicano successi e insuccessi.

Abbiamo $\left(\genfrac{}{}{0ex}{}{4}{2}\right)$ eventi, in generale $\left(\genfrac{}{}{0ex}{}{n}{k}\right)$.

Adesso se calcoliamo la probabilità di tutti questi eventi:

$$\begin{array}{rl}P(X=2)& =P(E_{SSII})+\cdots +P(E_{ISSI})\\ & =p\cdot p\cdot (1-p)\cdot (1-p))+\cdots +((1-p)\cdot p\cdot p\cdot (1-p))\end{array}$$

Hanno tutti la stessa probabilità che è data da $p^2\cdot (1-p{)}^2$ quindi è uguale a:

$$\left(\genfrac{}{}{0ex}{}{4}{2}\right)\cdot p^2\cdot (1-p{)}^2$$

Ovviamente abbiamo $p=2$ e quindi $n-k=2$ ma dipende da quanti esiti con successo abbiamo. Vale quindi la proposizione generale vista sopra.

Definizione

Una v.a. binomiale di paramentri $n\in \{1,2,3,\dots \}$ e $p\in [0,1]$ è una v.a. che assume valori $0,1,2,\dots ,n$ con la stessa probabilità:

$$P(X=k)=\left(\genfrac{}{}{0ex}{}{n}{k}\right)\cdot p^k\cdot (1-p{)}^k\forall k\in \{0,1,2,\dots ,n\}$$

Teorema

Indichiamo con $X=Bin(n,p)$ una v. binomiale di parametri $n,p$.

Sia $X=Bin(n,p)$ allora:

$$E[X]=n\cdot p\text{ e }Var(X)=n\cdot p\cdot (1-p)$$

Se $n=1$ e $X=Bin(n,p)$ ho che $X$ assume i valori $0,1$ e:

$$P(X=1)=\left(\genfrac{}{}{0ex}{}{n}{1}\right)\cdot p^1\cdot (1-p{)}^{n-1}=(\genfrac{}{}{0ex}{}{1}{1})p^1(1-p{)}^0=p$$

Mentre

$$P(X=0)=1-p$$

Quindi notiamo che $Bin(1,0)=Bernoulli(p)$ ovvero una variabile aleatoria di Bernoulli di parametro $p$.

Esercizio

Lancio 5 volte una moneta onesta. Sia $X=\#\text{Teste Uscite}$ determinare la probabilità discreta di $X,EX,Var(X),\sigma (X)$.

Dobbiamo riconoscere che è binomiale!

Infatti $X=Bin\left(5,\frac{1}{2}\right)$ ovvero 5 prove e il successo è che esce testa.

Calcoliamo $P_X$, sappiamo che $X$ assume $0,1,2,3,4,5$ ovvero le possibili teste quindi per questi valori $k$ calcoliamo:

Poi abbiamo che:

$$E[X]=np=5\cdot \frac{1}{2}=2.5$$ $$Var(X)=np(1-p)=5\cdot \frac{1}{2}\cdot \frac{1}{2}=1.25$$ $${\sigma }_X=\sqrt{1.25}=1.118$$

---

Perché le costanti additive non importano nella varianza?

Prendiamo come esempio due grafici di due probabilità:

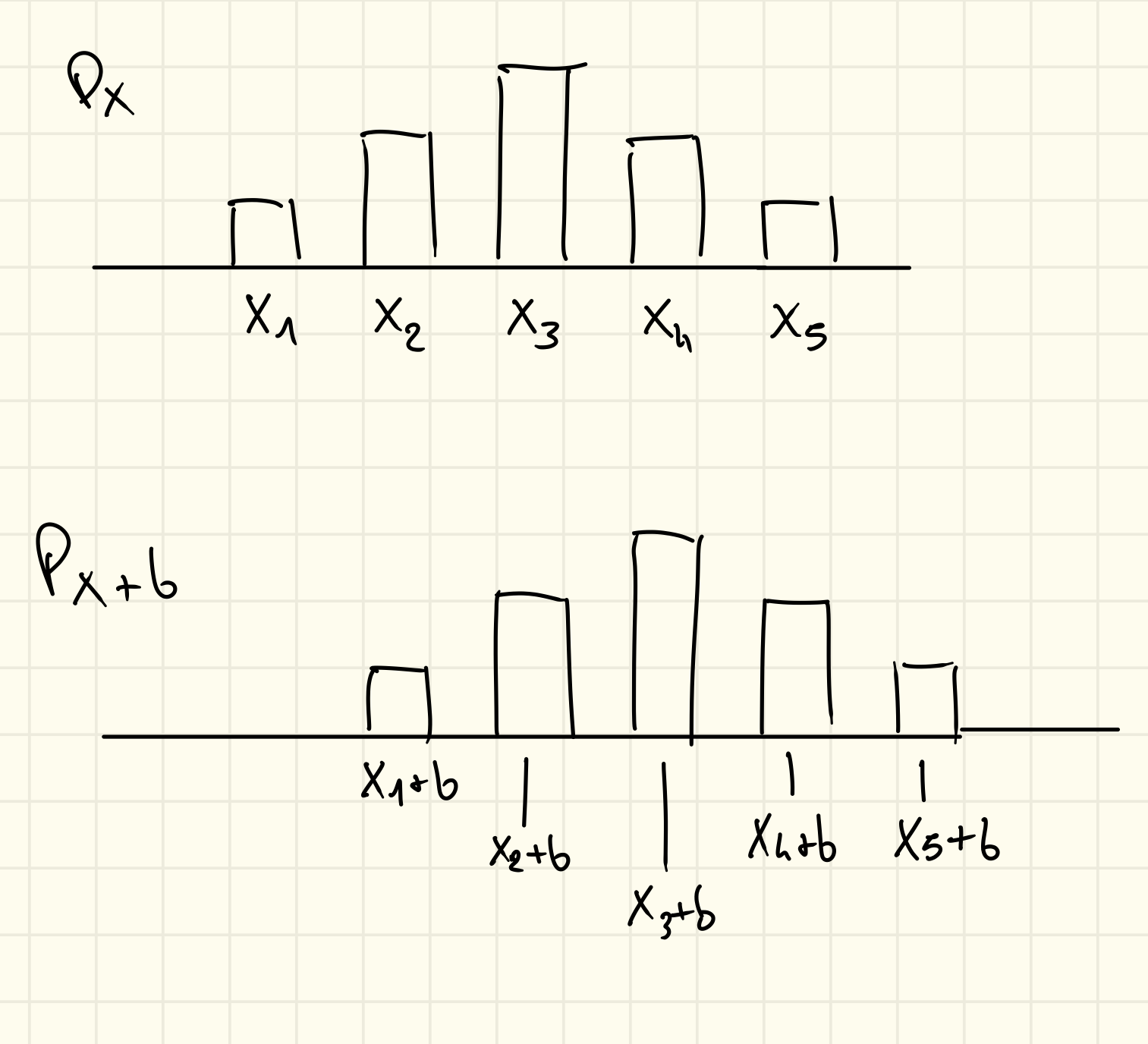
Notiamo che se trasliamo la probabilità di una costante, i grafici rimangono uguali ma vengono traslati, la varianza quindi rimane la stessa, dato che misura la dispersione dal valore atteso.

Quindi $Var(X)$ e $Var(X+b)$ coincidono.

Per vederlo meglio:

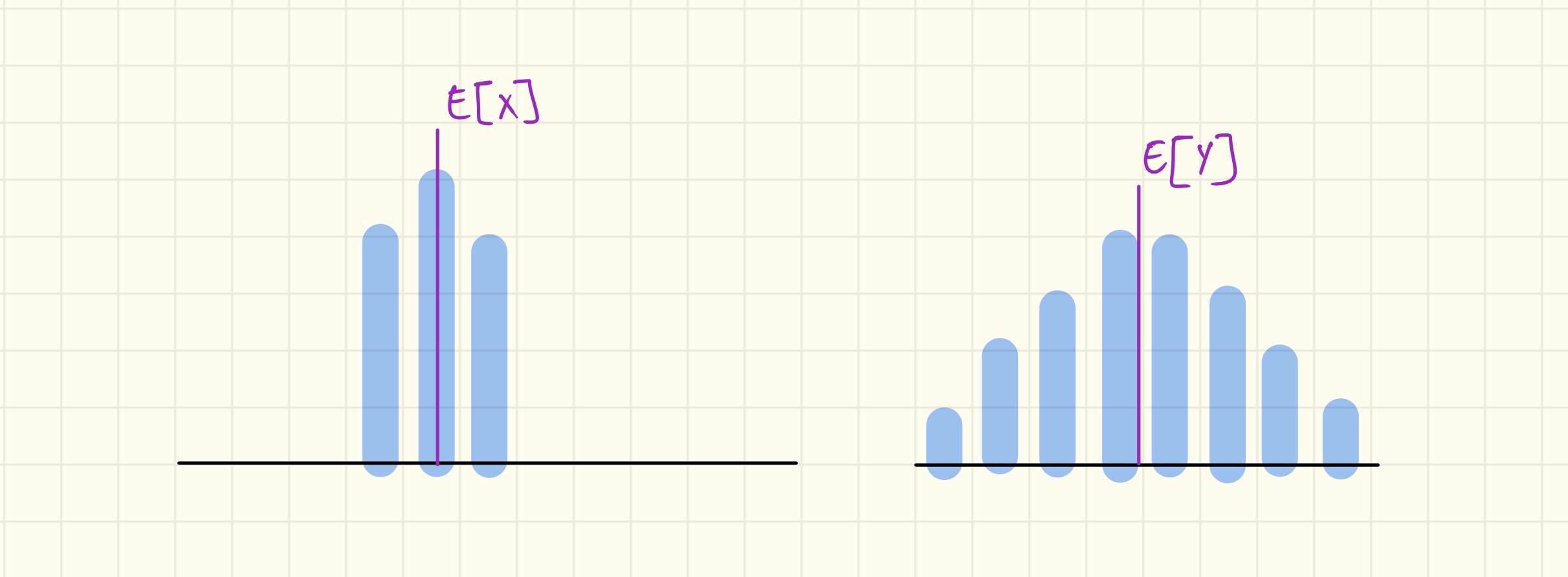
Qui infatti abbiamo che $Var(X)<Var(Y)$, notiamo infatti che nel grafico di $P_Y$ abbiamo più dispersione dal valore atteso rispetto al grafico di $P_X$

Variabile Aleatoria di Poisson

Una variabile aleatoria $X$ è detta di Poisson di parametro $\lambda >0$ se assume valori $0,1,2\dots$(tutti valori interi) e:

$$P_X(k)=P(X=k)=e^{-\lambda }\cdot \frac{{\lambda }^k}{k!}\forall k=0,1,2,\dots$$

Per verificare l’esistenza della variabile aleatoria di Poisson di parametro $k$ devo verificare:

$$\{\begin{array}{l}{P}_X(k)\ge 0\forall k=0,1,2,\dots \\ \\ \sum _{k=0}^{\infty }{P}_X(k)=1\end{array}$$

Infatti:

$$\sum _{k=0}^{\infty }{P}_X(k)=\sum _{k=0}^{\infty }{e}^{-\lambda }\cdot \frac{{\lambda }^k}{k!}=e^{-\lambda }\cdot \underset{\text{Serie Esponenziale}}{\underbrace{\sum _{k=0}^{\infty }\frac{{\lambda }^k}{k!}U}}=e^{-\lambda }\cdot e^{\lambda }=1$$

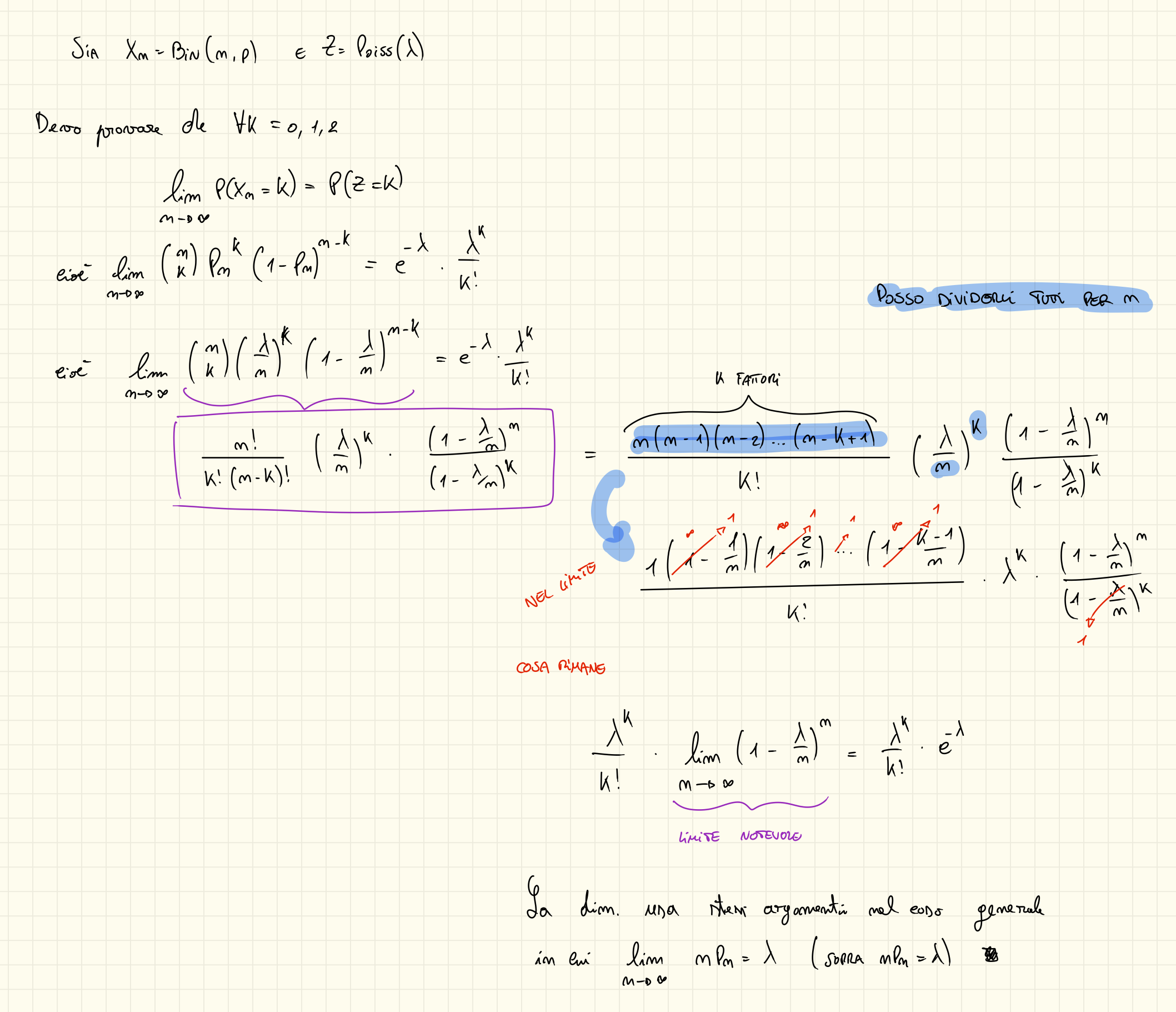
La variabile aleatoria di Poisson è un’approssimazione della variabile aleatoria binomiale $Bin(n,p)$ quando $n$ è molto grande e $p$ è piccolo, più precisamente:

Teorema, Legge dei piccoli numeri

Dato $n\in \{1,2,\dots \}$ sia $P_n\in [0,1]$ tale che:

$$\exists \underset{n\to \infty }{\lim }n{P}_n=:\lambda >0$$

Allora posto $X_n=Bin(n,P_n)$ e $Z=Pos(\lambda )$ ho:

$$\underset{n\to \infty }{\lim }P(X_n=k)=P(Z=k)\forall k\in \{0,1,2,\dots \}$$

Quindi per $n$ grande possiamo approssimare $P(X_n=k)\approx P(Z=K)$, quindi in alcune situazioni abbiamo che:

$$Bin(n,p)\approx Poisson(\lambda )$$

Dove presi $n,p,\lambda$ abbiamo che:

$$\begin{array}{rl}& n\gg 1\text{ (molto grande)}\\ & np\approx \lambda \text{ quindi anche }p\approx \frac{\lambda }{n}\end{array}$$

Cosa intendiamo per $Bin(n,p)\approx Poisson(\lambda )$? Intendiamo che:

$$P(X=k)\approx P(Z=k)\forall k=0,1,2,\dots$$

Dove $X=Bin(n,p)$ e $Z=Poisson(\lambda )$

Esempio di grandezza ben modellizzata da una variabile aleatoria di Poisson

Prendiamo la pagina di un libro e consideriamo la probabilità che un carattere venga stampato in modo errato. Quindi abbiamo una v.a. binomiale infatti un numero di prove $n$ e due esiti, successo se stampato male e insuccesso altrimenti.

Notiamo che $n$ è il numero di caratteri ed è molto alto all’interno di una pagina, e $p$ possiamo assumerla piccola.

Possiamo quindi assumere $Bin(n,p)\approx Poisson(\lambda )$ dove $\lambda =n\cdot p$

Esempio più concreto

Supponiamo che il numero di errori tipografici per pagina sia approssimato da $Poiss\left(\frac{1}{2}\right)$:

• Qual è la probabilità che ci sia almeno un errore a pagina 20?

Consideriamo quindi $z:=\#\text{Errori a pagina 20}$ e abbiamo quindi che:

$$\begin{array}{rl}& z=Poiss(\lambda )\lambda =\frac{1}{2}\\ & \\ & P(z=k)=e^{-\frac{1}{2}}\cdot {\left(\frac{1}{2}\right)}^k\cdot \frac{1}{k!}\end{array}$$

Possiamo considerare il fatto che ci sia almeno un errore come l’evento complementare di non ci sono errori, quindi possiamo calcolare:

$$P(z\ge 1)=1-P(z=0)=1-e^{-\frac{1}{2}}\cdot {\left(\frac{1}{2}\right)}^0\cdot \frac{1}{0!}=1-e^{-\frac{1}{2}}\approx 0.393$$

• Qual è la probabilità che ci siano esattamente 4 errori?

Dobbiamo quindi calcolare:

$$P(z=4)=e^{-\frac{1}{2}}\cdot {\left(\frac{1}{2}\right)}^4\cdot \frac{1}{4!}=\frac{1}{\sqrt{e}}\cdot \frac{1}{16}\cdot \frac{1}{24}\approx 0.00158$$

La Poisson approssima una binomiale $Poiss(\lambda )\approx Bin\left(n,\frac{\lambda }{n}\right)$ per un $n$ abbastanza grande

Teorema, Valore Atteso e Varianza Poisson

Se $X=Poiss(\lambda )$ allora $E[X]=\lambda$ e anche $Var(X)=\lambda$

---

Dimostrazione legge piccoli numeri, non mi va di scriverla per bene =P

---

Variabile Aleatoria Geometrica

Immaginiamo di ripetere in maniera indipendente una prova (lancio dado $\infty$ volte). Ogni prova ha successo con probabilità $p$ e insuccesso con $1-p$.

Sia $X$ il numero di prove necessarie per ottenere il primo successo.

$$P(X=k)k=1,2,3,\dots$$

Quindi:

$$P(X=k)=\underset{\text{Prova 1, ins.}}{\underbrace{(1-p)}}\cdot \underset{\text{Prova 2 ins.}}{\underbrace{(1-p)}}\cdot (1-p)\cdots p\to \text{Ultima prova, successo}$$

Quindi abbiamo che:

$$P(X=k)=(1-p{)}^{k-1}\cdot p\forall k=1,2,\dots$$

Tecnicamente però potrei sempre ottenere un insuccesso e quindi avere che $X=+\infty$ e quindi avrei che:

$$P(X=+\infty )=(1-p{)}^{\infty }=0\text{con }0<p<1$$

Questo significa che l’evento è possibile ma ha una probabilità nulla, questa strana situazione è data dal fatto che l’insieme degli esiti è un insieme non numerabile.

Oppure possiamo dimostrare che questo risultato è 0 svolgendo:

$$P(X=\infty )=1-P(X<\infty )=1-1=0$$

Dove

$$P(X<\infty )=\sum _{k=0}^{\infty }P(X=k)=\sum _{k=0}^{\infty }(1-p{)}^k\cdot p=p\underset{\text{Serie Geometrica}}{\underbrace{\sum _{k=0}^{\infty }(1-p{)}^k}}=p\cdot \frac{1}{1-(1-p)}=1$$

Infine possiamo dire che in una v.a. geometrica:

$$EX=\frac{1}{p}Var(X)=\frac{1-p}{p^2}$$

Esercizio

Lancio un dado finché non esce 6. a) Calcolare valore atteso del numero di lanci effettuati b) Calcolare probabilità di aver effettuato almeno 7 lanci

a)

$$\begin{array}{rl}& P(\text{Esce 6})=\frac{1}{6}=p\\ & X=\text{Lanci effettuati fino al primo 6}=Geom\left(\frac{1}{6}\right)\\ & E[X]=\frac{1}{\frac{1}{p}}=\frac{1}{\frac{1}{6}}=6\end{array}$$

b) Abbiamo $p=\frac{1}{6}$ come prima e anche la v.a. $X$. Adesso però dobbiamo calcolare $P(X=7)$

$$P(X=7)=(p{)}^{k-1}={\left(\frac{5}{6}\right)}^6$$

Variabile Aleatoria Binomiale Negativa

Dipende da due parametri, $p\in (0,1)$ che è la probabilità di successo in una prova e $r\in \{1,2,3\dots \}$ intero che indica il numero di successi che voglio ottenere.

Esempio Chiave

Considero una successione di prove indipendenti di tipo successo / insuccesso.

$$X:=\#\text{Prove effettuate fino ad avere }r\text{ successi per la prima volta}$$

Allora $X=\text{Bin\_Neg}(p,r)$, $X$ assume valori $r,r+1,r+2,\dots$ quindi dato $k\in \{r,r+1,r+2\dots \}$ come calcoliamo $P(X=k)$?

Sappiamo che sicuramente la k-esima prova deve avere come esito successo, mentre nelle k-1 prove dobbiamo avere sicuramente r-1 successi ma non ci importa in che ordine, possiamo quindi scriverlo come:

$$P(X=K)=P(\text{Ho r-1 successi nelle prime k-1 prove})\cdot p$$

A questo punto possiamo utilizzare la binomiale per calcolare la probabilità dei r-1 successi:

$$\left(\genfrac{}{}{0ex}{}{k-1}{r-1}\right)\cdot p^{r-1}\cdot (1-p{)}^{(k-1)-(r-1)}=(\genfrac{}{}{0ex}{}{k-1}{r-1})\cdot p^{r-1}\cdot (1-p{)}^{k-r}$$

Quindi moltiplicando per $p$ dell’ultimo successo otteniamo:

$$P(X=k)=\left(\genfrac{}{}{0ex}{}{k-1}{r-1}\right)\cdot p^r\cdot (1-p{)}^{k-r}$$

Inoltre sappiamo che:

$$X=\text{Bin\_Neg}(p,r)\Rightarrow E[X]=\frac{r}{p}Var(X)=\frac{r(1-p)}{p^2}$$

Osservazione

Se $r=1$ ovvero il numero di successi uguale a 1 otteniamo le stesse formule delle geometrica

Esercizio

In un gioco si estrae una pallina a caso da un’urna con 40 palline di cui una dorata, se si estrae quest’ultima si vince un peluche. Vogliamo giocare finché non vinciamo 2 peluche e ogni giocata costa 1.50 euro. Calcolare il valore atteso della spesa.

Definiamo:

• $X=\#\text{Numero di volte che giochiamo}$

• $Y=\text{Spesa Effettuata}$

  Che relazione c’è fra le due? $Y=1,5\cdot X$ e quindi $E[Y]=1,5\cdot E[X]$, calcoliamo il valore atteso di $X$ dato che è una binomiale negativa:

  $X=\text{Bin\_Neg}\left(p=\frac{1}{40},r=2\right)$ questo significa che possiamo calcolare il suo valore atteso con la formula:

E[X]=\frac{r}{p}=\frac{2}{\frac{1}{40}}=80

$$Equindi:$$

E[Y]=1,5\cdot 80 =120

Variabile Aleatoria Ipergeometrica

Prototipo: Abbiamo un’urna con $N$ palline di cui $m$ bianche e $N-m$ nere, estraggo senza rimpiazzo $n$ palline con $n\le N$.

Definiamo $X:=\#\text{Numero palline bianche estratte}$

$X$ è detta variabile aleatoria di parametri $N,m,n$

Come si calcola $P(X=k)?$ Numeriamo tutte le palline per distinguerle, nello spazio campionario abbiamo: $\left(\genfrac{}{}{0ex}{}{N}{n}\right)$ modi per scegliere $n$ palline. Usiamo il principio fondamentale della combinatoria:

$$P(X=k)=\frac{\left(\genfrac{}{}{0ex}{}{n}{k}\right)\cdot \left(\genfrac{}{}{0ex}{}{N-m}{n-k}\right)}{\left(\genfrac{}{}{0ex}{}{N}{n}\right)}$$

Quindi al numeratore abbiamo i modi per scegliere le bianche per i modi per scegliere le nere.

Per quali $k$ abbiamo che $P(X=k)>0$?

$$P(X=k)\iff \left(\genfrac{}{}{0ex}{}{m}{k}\right)>0\iff 0\le n-k\le N-m$$

Ricordiamo che per i binomiali $\left(\genfrac{}{}{0ex}{}{b}{a}\right)$ deve valere $0\le a\le b$ altrimenti è 0.

Quindi abbiamo:

$$\{\begin{array}{l}0\le k\le m\\ 0\le n-k\le N-m\end{array}$$

Ovvero 4 disuguaglianze:

$$\{\begin{array}{l}0\le k\\ k\le m\\ k\le n\\ n+m-N\le k\end{array}$$

Scritto in un’unica disuguaglianza:

$$max(0,n+m-N)\le k\le min(m,n)$$

Definizione

Una variabile aleatoria ipergeometrica di parametri $N,m,n$ è una variabile aleatoria discreta con densità di probabilità come il prototipo visto per l’esercizio sopra, cioè:

$$P(X=k)=\frac{\left(\genfrac{}{}{0ex}{}{n}{k}\right)\cdot \left(\genfrac{}{}{0ex}{}{N-m}{n-k}\right)}{\left(\genfrac{}{}{0ex}{}{N}{n}\right)}$$

Inoltre abbiamo che:

$$E[X]=\frac{n\cdot m}{N}Var(X)=np(1-p)\left(1-\frac{n-1}{N-1}\right)\text{dove }p=\frac{m}{N}$$

Esempio

Un rivenditore acquista componenti a lotti da 10, per ogni lotto controlla a caso 3 componenti e mantiene il lotto solo se i 3 componenti sono buoni. Il 30% dei lotti ha 4 componenti difettosi mentre il 70% ne ha soltanto 1 difettoso. Che % di lotti rifiuterà il rivendtiore?

Definiamo $X:=\#\text{Pezzi difettosi tra i 3 scelti dal lotto}$

Calcoliamo $P(X\ge 1)$ ovvero che ci sia almeno un pezzo difettoso.

$$\begin{array}{rl}& P(X\ge 1)=1-P(X=0)\\ & \\ & P(X=0)=P(X=0|E)P(E)+P(X=0|E^C)P(E^C)\\ & \text{Dove E indica che il lotto ha 4 pezzi difettosi}\\ & \\ & P(X=0|E)=\frac{\left(\genfrac{}{}{0ex}{}{4}{0}\right)\left(\genfrac{}{}{0ex}{}{6}{3}\right)}{\left(\genfrac{}{}{0ex}{}{10}{3}\right)}\\ & \\ & P(X=0|E^C)=\frac{\left(\genfrac{}{}{0ex}{}{1}{0}\right)\left(\genfrac{}{}{0ex}{}{9}{3}\right)}{\left(\genfrac{}{}{0ex}{}{10}{3}\right)}\\ & \\ & \text{Quindi:}\\ & \\ & P(X=0)=\frac{\left(\genfrac{}{}{0ex}{}{4}{0}\right)\left(\genfrac{}{}{0ex}{}{6}{3}\right)}{\left(\genfrac{}{}{0ex}{}{10}{3}\right)}\cdot 0.3+\frac{\left(\genfrac{}{}{0ex}{}{1}{0}\right)\left(\genfrac{}{}{0ex}{}{9}{3}\right)}{\left(\genfrac{}{}{0ex}{}{10}{3}\right)}\cdot 0.7\end{array}$$

Esempio

50 studenti di cui 7 con occhi verdi, scegliamo a caso 10 studenti, calcolare media e varianza di studenti con occhi verdi fra quelli scelti.

Abbiamo N=50, m=7 e n=10 mentre $X:=\#\text{Studenti con occhi verdi}$.

$$E[X]=\frac{nm}{N}=\frac{7}{5}$$

Mentre per la varianza:

$$Var(X)=10\cdot \frac{7}{50}\cdot \left(\frac{43}{50}\right)\cdot \left(1-\frac{9}{49}\right)$$

Infatti $p=\frac{7}{50}$

Osservazione

Prima abbiamo visto esempi senza rimpiazzo, cosa succede reinserendo ad esempio le palline estratte? Otteniamo semplicemente una binomiale, infatti avremo un numero di prove tutte uguali e indipendenti.

---

Recap Variabile Aleatoria

• $X$ variabile aleatoria è una funzione $X:S\to \mathbb{R}$
• $X$ è discreta se l’insieme dei possibili valori $\{x_i{\}}_{i\in I}$ è finito oppure infinito numerabile

In varaibili aleatorie discrete, abbiamo introdotto la densità di probabilità discreta $p_X:\{x_i{\}}_{i\in I}\to [0,1]$, definita come $p_X(x_i):=P(X=x_i)$.

Proposizione

$$\sum _{i\in I}{p}_X(x_i)=1\text{Per X v.a. discreta}$$

Dimostrazione

Definiamo $E_i:=\{X=x_i\}$ al variare di $i\in I$. Gli eventi $E_i$ sono una famiglia numerabile di eventi perché $X$ è una variabile aleatoria discreta, inoltre gli eventi sono 2 a 2 incompatibili.

Per l’additività finita se $I$ è finito e per l’additività numerabile se $I$ è infinito numerabile ho:

$$P\left(\bigcup _{i\in I}{E}_i\right)=\sum _{i\in I}P(E_i)$$

Inoltre notiamo che:

$$\bigcup _{i\in I}{E}_i=S\Rightarrow P(\bigcup _{i\in I}{E}_i)=P(S)=1$$

Infatti l’unione di tutti gli eventi è l’evento certo.

E quindi:

$$1=P\left(\bigcup _{i\in I}{E}_i\right)=\sum _{i\in I}\stackrel{\{X=x_i\}}{\overbrace{P(E_i)}}=\sum _{i\in I}{p}_X(x_i)$$

Osservazione

Se $X$ è v.a. generica allora non è vero che $\sum _{x}P(X=x)=1$ dove $x$ è un possibile valore di $X$.

Definizione

Date due v.a. $X$ e $Y$ definite sullo stesso spazio campionario, ovvero sono entrambe delle funzioni definite come $S\to \mathbb{R}$, entrambe discrete dove $X$ ha valori in $\{x_i{\}}_{i\in I}$ e $Y$ ha valori in $\{y_j{\}}_{j\in J}$.

La densità di probabilità discreta congiunta denotata con $p_{X,Y}$ è la funzione:

$$p_{X\times Y}:=\{x_i{\}}_{i\in I}\times \{y_j{\}}_{j\in J}\to [0,1]$$

È quindi definita sul prodotto cartesiano dei due insiemi, è inoltre definita come:

$$p_{X,Y}(x_i,y_j)=P(X=x_i,Y=y_j)$$

Esempio

Supponiamo di lanciare un dado 2 volte, chiamiamo $X:=\#\text{Lanci in cui ho faccia pari}$ e $Y:=\#\text{Lanci in cui esce multiplo di 3}$. Come calcoliamo $p_{X,Y}$?

$X$ ha valori in $\{0,1,2\}$ mentre $Y$ in $\{0,1,2\}$.

$$p_{X,Y}(x,y)=P(X=x,Y=y)$$

Dobbiamo calcolare quindi 9 valori

X/Y	0	1	2
0	$\frac{4}{36}$	$\frac{4}{36}$	$\frac{1}{36}$
1	$\frac{4}{36}$	$\frac{8}{36}$
2

Dove per ogni casella calcoliamo $P(X,Y)$ dove al posto di $X$ e $Y$ inseriamo il corrispondente valore della variabile aleatoria.

• Prima Riga
• $p_{X,Y}(0,2)=P(X=0,Y=2)=P(\{3,3\})=\frac{1}{36}$
• $p_{X,Y}(0,0)=P(X=0,Y=0)=\frac{2\cdot 3}{36}$
• $p_{X,Y}(0,1)=P(X=0,Y=1)=P((3,1),(3,5),(1,3),(5,3))=\frac{4}{36}$
• Seconda Riga
• $p_{X,Y}(1,0)=P(X=1,Y=0)=P((2,1),(2,5),(4,1),(4,5))=\frac{4}{36}$
• $p_{X,Y}(1,1)=P(X=1,Y=1)=P((2,3),(4,3),(1,6),(5,6),(6,5),(6,1))=\frac{8}{36}$
• $p_{X,Y}(1,2)=P(X=1,Y=2)=\dots$

Altro metodo è quello di fare la tabella con i casi, in questo caso un 6x6 e poi inserire in ogni casella la coppia di valori (x,y), poi contiamo quante caselle per ogni coppia di valori.

Se prendiamo lo stesso esempio ma lanciando il dado una sola volta abbiamo che:

$$\{\begin{array}{l}1X=0,Y=0\\ 2X=1,Y=0\\ 3X=0,Y=1\\ 4X=1,Y=0\\ 5X=0,Y=0\\ 6X=1,Y=1\end{array}$$

E inserendolo nella tabella:

X/Y	0	1
0	$\frac{2}{6}$	$\frac{1}{6}$
1	$\frac{2}{6}$	$\frac{1}{6}$

Notiamo che la somma di tutti i valori fa 1.

Proposizione

Siano $X$ e $Y$ v.a. discrete definite su $S$, sia $\{x_i{\}}_{i\in I}$ l’insieme dei possibili valori di $X$ e sia $\{y_j{\}}_{j\in J}$ l’insieme dei possibili valori di $Y$.

Allora:

1. $p_{X,Y}(x_i,y_j)\in [0,1]$
2. ${\sum }_{i\in I}{\sum }_{j\in J}{p}_{X,Y}(x_i,y_j)=1$
3. $p_X(x_i)={\sum }_{j\in J}{p}_{X,Y}(x_i,y_j)$
4. $p_Y(y_j)={\sum }_{i\in I}{p}_{X,Y}(x_i,y_j)$

Dimostrazione

1. $p_{X,Y}(x_i,y_j)\underset{definizione}{=}P(X=x_i,Y=y_j)\in [0,1]$
2. Questa dimostrazione usa le stesse idee della dimostrazione di $\sum _{i\in I}{p}_X(x_i)=1$

Poniamo $E_{ij}=\{X=x_i,Y=y_j\}$, abbiamo che $p_{X,Y}(x_i,y_j)\underset{definizione}{=}P(X=x_i,Y=y_j)=P(E_{ij})$.

Gli eventi $E_{ij}$ al variare di $i\in I,j\in J$ formano una famiglia finita o infinita numerabile di eventi 2 a 2 incompatibili.

Quindi:

$$\sum _{i\in I,j\in J}{p}_{X,Y}(x_i,y_j)=\sum _{i\in I,j\in J}P(E_i)\underset{\text{additivitaˋ}}{=}P\left(\bigcup _{i\in I,j\in J}{E}_{ij}\right)=P(S)=1$$

$$p_X(x_i)\underset{\text{definizione}}{=}P(X=x_i)=P\left(\bigcup _{j\in J}\{X=x_i,Y=y_j\}\right)=P\left(\bigcup _{j\in J}{E}_{ij}\right)=\sum _{j\in J}P(E_{ij})=\sum _{j\in J}{p}_{X,Y}(x_i,y_j)$$

4. Dimostrazione simile a (3).

Esempio

Ho variabili aleatorie $X,Y$ su $S$. $X$ assume valori $-2,0,5$ e $Y$ assume valori $4,9$. Inoltre $p_{X,Y}$ è data da:

X / Y	4	9
-2	$\frac{1}{10}$	$\frac{2}{10}$
0	$\frac{0}{10}$	$\frac{1}{10}$
5	$\frac{3}{10}$	$\frac{3}{10}$
Dobbiamo determinare $p_X$ e $p_Y$. Ricordiamo la formula:

$$p_X(x_i)=\sum _j{p}_{X,Y}(x_i,y_j)$$

Quindi calcolando $p_X$

$$p_X(-2)=p_{X,Y}(-2,4)+p_{X,Y}(-2,9)=\frac{1}{10}+\frac{2}{10}=\frac{3}{10}$$ $$p_X(0)=\frac{0}{10}+\frac{1}{10}=\frac{1}{10}$$ $$p_X(-2,9)=\frac{1}{10}+\frac{2}{10}=\frac{3}{10}$$ $$p_X(5)=\frac{3}{10}+\frac{3}{10}=\frac{6}{10}$$

Mentre per la $p_Y$:

$$p_Y(4)=p_{XY}(-2,4)+p_{XY}(0,4)+p_{XY}(5,4)=\frac{1}{10}+\frac{0}{10}+\frac{3}{10}=\frac{4}{10}$$ $$p_Y(9)=\frac{2}{10}+\frac{1}{10}+\frac{3}{10}=\frac{6}{10}$$

---

In una v.a. discreta congiunta, le densità che la compongono vengono chiamata marginali e conoscendo la congiunta possiamo calcolare le marginali, ma non vale il contrario.

Vediamo un esempio

Abbiamo un’urna con 6 palline numerate da 1 a 6, estraiamo 2 palline con rimpiazzo e definiamo:

$$\begin{array}{rl}& X:=\text{Numero della prima pallina}\\ & Y:=\text{Numero della seconda pallina}\end{array}$$

Quindi $X$ assume valori in $\{1,2,3,4,5,6\}$ e con $p_X(k)=\frac{1}{6}$ per ogni $k$ da 1 a 6, analogamente per $Y$.

La congiunta $(X,Y)$ assume valori $(a,b)$ con $a,b\in \{1,2,3,4,5,6\}$ e $p_{X,Y}(a,b)=P(X=a,Y=b)=\frac{1}{36}$ $\forall (a,b)\in \{1,2,3,4,5,6{\}}^2$

Adesso facciamo lo stesso esempio ma senza rimpiazzo:

Quindi le due marginali sono identiche ma per la congiunta abbiamo che:

$$p_{X,Y}(a,b)=\{\begin{array}{l}\frac{1}{30}\text{ se }a,b\in \{1,\dots ,6\}\text{ e }a\ne b\\ 0\text{ se }a,b\in \{1,\dots ,6\}\text{ e }a=b\end{array}$$

Infatti la congiunta assume valori $(a,b)$ dove $a,b\in \{1,\dots ,6\}$ ma $a\ne b$.

Notiamo quindi che nei due esperimenti le due marginali sono uguali ma la congiunta dipende dall’esperimento e quindi cambia.

Definizione

Se ho $n$ v.a. discrete $X_1,\dots X_n:S\to \mathbb{R}$ dove $X_i$ ha valori in $V_i$ con $i=1,\dots ,n$ la densità di probabilità discreta congiunta è data da $p_{X_1,\dots ,X_n}:V_1\times \cdots \times V_n\to [0,1]$ ed è definita come $p_{X_1,\dots ,X_n}(a_1,\dots ,a_n):=P(X_1=a_1,\dots ,X_n=a_n)$

Adesso torniamo ad un esempio con 2 v.a. definite quindi $X,Y:S\to \mathbb{R}$ e la loro congiunta definite come:

$$\begin{array}{rl}& X:S\to \mathbb{R}S\to X_S\\ & Y:S\to \mathbb{R}S\to Y_S\\ & (X,Y):S\to {\mathbb{R}}^{2}S\to (X_S,Y_S)\end{array}$$

Supponiamo di avere una funzione composta $f:{\mathbb{R}}^2\to \mathbb{R}$ definita:

$$f(X,Y):S\to \mathbb{R}S\to f(X_S,Y_S)$$

Questa è una v.a. dato che va da $S$ in $\mathbb{R}$ e se $X,Y$ sono discrete allora lo è anche $f$ dato che se applichiamo una funzione, la cardinalità del codominio è sicuramente minore o uguale a quella del dominio.

Adesso data una v.a. di questo tipo, calcoliamo il valore atteso.

Proposizione

Siano $X,Y$ v.a. discrete e $f:{\mathbb{R}}^2\to \mathbb{R}$ allora:

$$E[f(X,Y)]=\sum _{i\in I}\sum _{j\in J}f(x_i,y_j)P_{X,Y}(x_i,y_j)$$

Dove $\{x_i{\}}_{i\in I}$ è l’insieme dei valori di $X$ e $\{y_j{\}}_{j\in J}$ è l’insieme dei valori di $Y$.

Esempio

Data la v.a.

Calcolare $E[X^{2}Y]={\sum }_i{\sum }_j{x}_i^2{y}_j{P}_{X,Y}(x_i,y_j)$ dove $f:{\mathbb{R}}^2\to \mathbb{R}$ e definita come $f(a,b)=a^{2}b$, eseguiamo i calcoli:

$$E[X^{2}Y]=(-1{)}^2\cdot 0\cdot \frac{2}{10}+(-1{)}^2\cdot 2\cdot \frac{1}{10}+(-1{)}^2\cdot 3\cdot 0+\cdots =\frac{45}{10}$$

Proposizione

$E[X+Y]=E[X]+E[Y]$

Dimostrazione

Abbiamo $f:{\mathbb{R}}^2\to \mathbb{R}$ definita da $f(a,b)=a+b$ ovvero $f(X,Y)=X+Y$, possiamo quindi vederla come una funzione e usare la proposizione precedente per calcolare il valore atteso:

$$\begin{array}{rl}E[X+Y]& =E[f(X,Y)]\\ & =\sum _i\sum _j\underset{x_i+y_j}{\underbrace{f(x_i,y_j)}}{P}_{X,Y}(x_i,y_j)\\ & =\sum _i\sum _j{x}_i{P}_{X,Y}(x_i,y_j)U+\sum _i\sum _j{y}_i{P}_{X,Y}(x_i,y_j)\\ & =\sum _i{x}_i\underset{\text{Ruota solo la j, eˋ il calcolo di }{P}_X}{\underbrace{\left(\sum _j{P}_{X,Y}(x_i,y_j)U\right)}}+\sum _j{y}_j\underset{\text{Ruota solo la i, eˋ il calcolo di }{P}_Y}{\underbrace{\left(\sum _i{P}_{X,Y}(x_i,y_j)\right)}}\\ & =\underset{E[X]}{\underbrace{\sum _i{x}_i{P}_X(x_i)}}+\underset{E[Y]}{\underbrace{\sum _j{y}_j{P}_Y(y_j)}}\\ & =E[X]+E[Y]\end{array}$$

In modo analogo si ottiene che:

Proposizione

$$E[X_1+\cdots +X_n]=E[X_1]+\cdots +E[X_n]$$

In generali dati $a_1,\dots ,a_n\in \mathbb{R}$ si ha che:

$$E[a_{1}X+\cdots +a_n{X}_n]=a_{1}E[X_1]+\cdots +a_{n}E[X_n]$$

Esempio

Lancio un dado 1000 volte, calcolare $E[X]$ dove $X=\text{\#Esce 5}$, notiamo che usando la binomiale quindi $X=Bin(1000,1/6)$ si ha che:

$$E[X]=\sum _{k=0}^{1}000k\left(\genfrac{}{}{0ex}{}{1000}{k}\right){\left(\frac{1}{6}\right)}^k{\left(\frac{5}{6}\right)}^{1000-k}$$

Ed è molto calcoloso.

È meglio scomporre questa variabile aleatoria in 1000 variabili più semplici piuttosto che eseguire il calcolo.

Possiamo scomporla in $X_1,\dots ,X_{1000}$ dove $X_i$ vale 1 se alla i-esima prova esce 5, 0 altrimenti, in questo modo otteniamo:

$$E[X]=\sum _{i=1}^{1000}\underset{1\cdot \frac{1}{6}+0\cdot \frac{5}{6}}{\underbrace{E[X_i]}}=1000\cdot \frac{1}{6}$$

Da cui abbiamo trovato la formula $E[X]=np$ per le binomiali, infatti in questo caso abbiamo $n=1000$ e $p=\frac{1}{6}$

Proposizione

Se $X=Bin(n,p)\Rightarrow E[X]=np$

Dimostrazione

$X=\#Successi$ in $n$ prove indipendenti dove $p=\text{prob. successo}$ allora $X=X_1+\cdots +X_n$ dove $X_i$ vale 1 se la i-esima prova ha successo, 0 altrimenti. Allora:

$$E[X]=E\left[\sum _{i=1}^n{X}_i\right]=\sum _{i=1}^n\underset{1\cdot p+0\cdot (1-p)}{\underbrace{E[X_i]}}=np$$

---

Prendiamo un’urna con $N$ palline di cui $m$ bianche e $N-m$ nere, estraiamo $n$ palline senza rimpiazzo, questo possiamo farlo in due modi.

1. Estraiamo $n$ palline in un unico blocco
2. Estraiamo una pallina alla volta senza rimpiazzo

Pensiamo al caso di estrarre una pallina alla volta, definiamo quindi: $E_i=$ La i-esima pallina estratta è bianca.

$$\begin{array}{rl}& E_1=\frac{m}{N}\\ & \dots \\ & E_3=?\end{array}$$

Possiamo calcolare $E_3$ usando la combinatoria ma per altri motivi (?) possiamo dire che:

$$P(E_1)=P(E_2)=\cdots =P(E_n)(\ast )$$

Quindi sapendo $(\ast )$ possiamo dire che:

$$P(E_i)=\frac{m}{N}\forall i=1,\dots ,n$$

Ma perché vale $(\ast )$?

Prendiamo l’urna e numeriamo le palline per distinguerle:

$$U=\{B_1,B_2,\dots ,B_m,N_1,N_2,\dots ,N_{N-m}\}$$

E abbiamo come spazio campionario:

$$S=\{(x_1,x_2,\dots ,x_n):x_i\in U\forall i,x_1,\dots ,x_n\text{ distinti}\}$$

Abbiamo tutti esiti equiprobabili e quindi $P(E)=\frac{|E|}{|S|}$ $\forall E\subset S$ evento. Adesso supponiamo di avere una mappa bigettiva $f:S\to S$ quindi $\forall E\subset S$ abbiamo che $|E|=|f(E)|$ e quindi:

$$P(E)=\frac{|E|}{|S|}=\frac{|f(E)|}{|S|}=P(f(E))$$

Cosa abbiamo imparato?

$$\forall f:S\to S\text{ bigettiva}$$

Si ha che:

$$P(E)=P(f(E))\forall E\subset S\text{ evento}$$

Adesso dimostriamo $(\ast )$, più precisamente che $P(E_1)=P(E_i)$ $i=2,3,\dots ,n$.

Scegliamo $i\in \{2,3,\dots ,n\}$ e abbiamo che $E_1=\{(x_1,\dots ,x_n)\in S:x_1\in \{B_1,B_2,\dots ,B_m\}\}$. Possiamo esibire $f:S\to S$ bigettiva tale che $f(E_1)=E_i$? Se possiamo farlo allora abbiamo che $P(E)=P(f(E_1))=P(E_i)$ .

Prendiamo ad esempio $i=3$, abbiamo $f(x_1,x_2,x_3,\dots ,x_n)=\{x_3,x_2,x_1,\dots ,x_n\}$ ovvero $f$ scambia la prima con la i-esima entrata.

Esempio

Scegliamo 5 studenti da interrogare e definiamo:

• E = Il secondo e il terzo studente scelto sono maschi.
• F = Il quarto e il quinto studente scelto sono maschi.

Abbiamo $C$ come classe e il nostro spazio campionario è:

$$\begin{array}{rl}& S=\{(x_1,x_2,\dots ,x_5):x_i\in C\forall i,x_1,\dots ,x_5\text{ distinti}\}\\ & E=\{(x_1,x_2,\dots ,x_5)\in S:x_2,x_3\text{ sono maschi}\}\\ & F=\{(x_1,\dots ,x_5)\in S:x_4,x_5\text{ sono maschi}\}\end{array}$$

Abbiamo che $P(E)=P(F)$ se esibiamo $f:S\to S$ bigettiva tale che $f(E)=F$, possiamo definire:

$$f(x_1,x_2,x_3,x_4,x_5)=(x_1,x_4,x_5,x_2,x_3)$$

Ovvero che scambia il 2 con il 4 e il 3 con il 5.

Questo metodo vale sempre se si lavora con spazi di probabilità che hanno esiti equiprobabili.

Proposizione

Sia $S$ uno spazio di probabilità con esiti equiprobabili e sia $f:S\to S$ una bigezione. Allora $P(E)=P(f(E))$ $\forall E\subset S$.

Dimostrazione

$$P(E)\underset{\text{esiti quiprobabili}}{=}\frac{|E|}{|S|}\underset{\text{f eˋ bigettiva}}{=}\frac{|f(E)|}{|S|}\underset{\text{esiti equiprobabili}}{=}P(f(E))$$

Proposizione

Sia $X$ v.a. ipergeometrica con paramentri $N,m,n$ (con il prototipo visto nella ipergeometrica) abbiamo $E[X]=\frac{nm}{N}$

Dimostrazione

Estraiamo le palline una alla volta e scomponiamo $X=X_1+X_2+\cdots +X_n$ dove ogni v.a. $X_i$ vale 1 se la i-esima pallina è bianca, 0 altrimenti. Otteniamo quindi:

$$E[X]=\sum _{i=1}^{n}E[X_i]=\frac{nm}{N}$$

Infatti:

$$E[X_i]=1\cdot P(E_i)+0\cdot P(E_i^C)=P(E_i)=P(E_1)=\frac{m}{N}$$

Se le $n$ estrazioni sono con rimpiazzo allora $X$ è una v.a. binomiale, infatti con il rimpiazzo tutti gli esperimenti sono identici e non si influenzano. Per dimostrarlo abbiamo usato la linearità del valore atteso in modo molto semplice, altrimenti avremmo dovuto usare metodi più complessi.

Definizione - Variabili Aleatorie Indipendenti

Date $X_1,X_2,\dots ,X_n$ v.a. sullo stesso spazio campionario, queste sono indipendenti se:

$$P(X_1\in A_1,\dots ,X_n\in A_n)=P(X_1\in A_1),\dots ,P(X_n\in A_n)\forall A_1,\dots ,A_n\subset \mathbb{R}$$

Se ho un esperimento formato da sottoesperimenti operativamente indipendenti, ovvero che non si influenzano allora variabili aleatorie che si riferiscono a sottoesperimenti diversi sono tra loro indipendenti.

Esempio

Lanciamo un dado 20 volte, definiamo

$$\begin{array}{rl}& X:=\text{Numero uscito al 3° lancio}\\ & Y:=\text{Numero uscito al 9° lancio}\\ & Z:=\text{Numero uscito al 17° lancio}\end{array}$$

Possiamo provare che $X,Y,Z$ sono v.a. indipendenti.

Proposizione

Siano $X:S\to \mathbb{R}$ e $Y:S\to \mathbb{R}$ v.a. discrete, $X$ assume valori $\{x_i{\}}_{i\in I}$ e $Y$ assume valori $\{y_j{\}}_{j\in J}$. Allora $X,Y$ sono indipendenti se e solo se:

$$p_{X,Y}(x_i,y_j)=p_X(x_i)p_Y(y_j)\forall i\in I,j\in J$$

Nota

Per decidere se $X$ e $Y$ sono indipendenti o meno mi basta sapere $p_{X,Y}$ infatti $p_X(x_i)={\sum }_j{p}_{X,Y}(x_i,y_j)$ e $p_Y(y_j)={\sum }_i{p}_{X,Y}(x_i,y_j)$.

Dimostrazione Proposizione

---

Covarianza di variabili aleatorie

Date 2 v.a. $X,Y:S\to \mathbb{R}$, ovvero che hanno lo stesso spazio campionario, la covarianza di $X$ e $Y$ è data da:

$$Cov(X,Y)=E[(X-EX)\cdot (Y-EY)]$$

Questa ha varie proprietà

1. $Cov(X,X)=Var(X)$

Dimostrazione

$$Cov(X,X)=E[(X-EX)(X-EX)]=E[(X-EX{)}^2]=Var(X)$$

2. $Cov(X,Y)=Cov(Y,X)$

Dimostrazione

$Cov(X,Y)=E[(X-EX)(Y-EY)]=E[(Y-EY)(X-EX)]=Cov(Y,X)$

3. $Cov(X,Y)=E[XY]-E[X]E[Y]$

Notiamo infatti che se $Y=X$ riotteniamo la varianza di X ma nell’altra forma ovvero $Var(X)=E[X^2]-(E[X]{)}^2$

Dimostrazione

$$\begin{array}{rl}Cov(X,Y)=E[(X-EX)(Y-EY)]& =E[XY-X\cdot EY-EX\cdot Y+EX\cdot EY]\\ \text{Per linearitaˋ di E}& =E[XY]-EX\cdot EY\cancel{-EX\cdot EY}+\cancel{EX\cdot EY}\\ & =E[XY]-EX\cdot EY\end{array}$$

La covarianza gode della linearità? Si

• Proprietà 1

Siano $X,Y,Z:S\to \mathbb{R}$ v.a. e siano $a,b\in \mathbb{R}$:

$$Cov(aX+bY,Z)=aCov(X,Z)+bCov(Y,Z)$$

Dimostrazione

$$\begin{array}{rl}Cov(aX+bY,Z)& =E[(aX+bY-\underset{aEX+bEY}{\underbrace{E[aX+bY]}})(Z-EZ)]\\ & =E[(aX+bY-aEX-bEY)(Z-EZ)]\\ & =E[(a(X-EX)+b(E-EY))(Z-EZ)]\\ & =E[a(X-EX)(Z-EZ)+b(Y-EY)(Z-EZ)]\\ \text{Linearitaˋ di E}& =aE[(X-EX)(Z-EZ)]+bE[(Y-EY)(Z-EZ)]\\ \text{Definizione cov}& =aCov(X,Z)+bCov(Y,Z)\end{array}$$

• Proprietà 2

È analoga alla precedente ma in direzione opposta, quindi date $X,Y,Z:S\to \mathbb{R}$ e dati $a,b\in \mathbb{R}$ allora:

$$Cov(Z,aX+bY)=aCov(X,Z)+bCov(Y,Z)$$

La dimostrazione è simile alla precedente.

---

Le due proprietà appena viste implicano la linearità, quindi:

$$Cov\left(\sum _{k=1}^n{a}_k{X}_k,\sum _{j=1}^m{b}_j{Y}_j\right)=\sum _{k=1}^n\sum _{j=1}^m{a}_k{b}_{j}Cov(X_k,Y_j)$$

Idea Utilizzo:

$$\begin{array}{rl}& Cov(2X_1-3X_2,-4Y_1+Y_2)=\\ & \\ & \text{Proprietaˋ 1:}\\ & =2Cov(X_1,-4Y_1+Y_2)-3Cov(X_2,-4Y_1+Y_2)\\ & \\ & \text{Proprietaˋ 2:}\\ & =2\cdot (-4)\cdot Cov(X_1,Y_1)+2\cdot 1\cdot Cov(X_1,Y_2)-3\cdot (-4)\cdot Cov(X_2,Y_1)-3\cdot 1\cdot Cov(X_2,Y_2)\\ & =-8Cov(X_1,Y_1)+2Cov(X_1,Y_2)+12Cov(X_2,Y_1)-3Cov(X_2,Y_2)\end{array}$$

---

Proposizione

Se $X_1,X_2,\dots ,X_n:S\to \mathbb{R}$ allora $Var(X_1+\cdots +X_n)$:

$$\sum _{i=1}^{n}Var(X_i)+2\sum _{1\le i\le j\le n}Cov(X_i,X_j)(1)$$

Se le v.a. sono 2 a 2 non correlate ovvero se $Cov(X_i,X_j)=0$ $\forall i\ne j$ allora:

$$Var(X_1+\cdots +X_n)=\sum _{i=1}^{n}Var(X_i)(2)$$

La proprietà (1) implica la (2) se siamo sotto l’ipotesi detta prima, quindi dobbiamo dimostrare soltanto (1)

Dimostrazione

$$Var(X_1+\cdots +X_n)=Cov(X_1+\cdots +X_n,X_1+\cdots +X_n)$$

Per bilinearità possiamo dire che che la covarianza è uguale:

$$\sum _{k=1}^n\sum _{j=1}^{n}Cov(X_k,X_j)=\sum _{k=1}^{n}Cov(X_k,X_k)\dots$$

Da continuare non l’ho ben capita (ma tanto a l’esame non c’è, letsgoski 🤙🏻.

---

Notiamo che la regola, in generale, funziona come il quadrato di binomio, infatti:

$$Var(X+Y)=Var(X)+Var(Y)+2Cov(X,Y)$$

Proposizione

Se $X,Y$ sono v.a. indipendenti allora $E[XY]=E[X]E[Y]$ e quindi $Cov(X,Y)=0$

Dimostrazione

Per dimostrarlo ci servono due cose:

1. $E[f(X,Y)]={\sum }_i{\sum }_{j}f(x_i,y_j)p_{X,Y}(x_i,y_j)$
2. $p_{X,Y}(x_i,y_j)=p_X(x_i)p_Y(y_j)$

$$\begin{array}{rl}E[XY]& =\sum _i\sum _j{x}_i{y}_j{p}_{X,Y}(x_i,y_j)(1)\\ & =\sum _i\sum _k{x}_i{y}_j{p}_X(x_i)p_Y(y_j)(2)\\ \text{Distribuiamo}& =\underset{E[X]}{\underbrace{\left(\sum _i{x}_i{p}_X(x_i)U\right)}}\underset{E[Y]}{\underbrace{\left(\sum _j{y}_j{p}_Y(y_j)\right)}}=E[X]E[Y]\end{array}$$

Proposizione

Se $X,Y$ sono v.a. indipendenti e $f:\mathbb{R}\to \mathbb{R}$ e $g:\mathbb{R}\to \mathbb{R}$ allora anche $f(X)$ e $g(Y)$ sono indipendenti, per dimostrarlo, dire che le funzioni applicate alla v.a. sono indipendenti significa che $\forall A,B\subset \mathbb{R}$ vale:

$$P(f(X)\in A,g(Y)\in B)=P(f(X)\in A)P(g(Y)\in B)$$

Proviamolo:

$$\begin{array}{rl}P(f(X)\in A,g(Y)\in B)& =P(X\in f^{-1}(A),Y\in g^{-1}(B))\\ & =P(X\in f^{-1}(A))P(Y\in f^{-1}(B))\\ & =P(f(X)\in A)P(g(Y)\in B)\end{array}$$

---

Ricordiamo

• $X,Y$ non correlate se $Cov(X,Y)=0$
• $X,Y$ sono indipendenti se $P(X\in A,Y\in B)=P(X\in A)P(Y\in B)$ $\forall A,B\subset \mathbb{R}$

Notiamo che se $X,Y$ sono indipendenti, allora $Cov(X,Y)=0$, vale anche il contrario? No, esistono v.a. dipendenti con $Cov(X,Y)=0$

Corollario

Se $X_1,\dots ,X_n$ sono v.a. indipendenti allora $Var\left({\sum }_{i=1}^n{x}_i\right)={\sum }_{i=1}^n(x_i)$

Applicazione - Proposizione

$$X=Bin(n,p)\Rightarrow Var(X)=np(1-p)$$

Dimostrazione

Prendo $n$ prove indipendenti di tipo successo / insuccesso:

$$\begin{array}{rl}& X:=\#\text{Successi Ottenuti}\\ & X=X_1+\cdots +X_n\end{array}$$

Quindi $X_i$ vale 1 se la i-esima prova è un successo, 0 altrimenti. Dato che le prove sono indipendenti, per il corollario possiamo dire:

$$\begin{array}{rl}Var(X)& =\sum _{i=1}^n\underset{E[X_i^2]-(E[X_i]{)}^2}{\underbrace{Var(X_i)}}\\ & =(1\cdot p+0\cdot (1-p))-(1\cdot p+0\cdot (1-p){)}^2\\ & =p\cdot (1-p)\end{array}$$

Esercizio

Lanciamo una moneta truccata 100 volte, sappiamo che esce testa con probabilità $\frac{2}{3}$ e croce con $\frac{1}{3}$. Definiamo $X=\text{Teste Ottenute}$ e $Y=\text{Croci ottenute}$. Calcolare $Cov(X,Y)$.

Sappiamo che $X+Y=100$ e quindi possiamo scrivere $Y=100-X$ e quindi dobbiamo calcolare $Cov(X,100-X)$.

Per bilinearità possiamo dire $Cov(X,100-X)=Cov(X,100)-Cov(X,X)$, calcoliamo quindi:

$$Cov(X,100)=E[X\cdot 100]-E[X]\cdot E[100]=100\cdot E[X]-E[X]\cdot 100=0$$

Quindi $Cov(X,Y)=0-Cov(X,X)=-Var(X)=-\frac{200}{9}$, infatti calcolando $Var(X)$ otteniamo:

$$X=Bin\left(100,\frac{2}{3}\right)\Rightarrow Var(X)=np(1-p)=100\cdot \frac{2}{3}\cdot \frac{1}{3}$$

Esercizio

Variabile Aleatorie Continue

Ricordiamo che:

• $X$ v.a. è una funzione definita come $X:S\to \mathbb{R}$
• $X$ è detta discreta se $X$ assume valori $\{x_i{\}}_{i\in I}$ insieme finito, oppure infinito ma numerabile

Definizione v.a. continua

Una v.a. $X:S\to \mathbb{R}$ è detta continua se esiste $f:\mathbb{R}\to [0,+\infty )$ t.c. $P(X\in A)=\underset{A}{\int }f(x_a)dx$, la funzione $f$ è detta funzione di densità

Definizione v.a. uniforme

Una v.a. $X$ è detta uniforme sull’intervallo $(a,b)$ se è continua con funzione di densità:

$$f(x)=\{\begin{array}{l}\frac{1}{b-a}\text{ se }x\in (a,b)\\ 0\text{ altrimenti}\end{array}$$

(Anche con intervalli chiusi)

Prendiamo $[a,b]=[0,1]$, sia $A\subset [0,1]$ allora $P(X\in A)$:

$${\int }_{A}f(x)dx={\int }_{A}1dx=\text{Lunghezza di A}=L(A)$$

Ad esempio se $P\left(X\in \left(\frac{1}{2},\frac{3}{4}\right)\right)=L\left(\left(\frac{1}{2},\frac{3}{4}\right)\right)=\frac{3}{4}-\frac{1}{2}=\frac{1}{4}$, infatti la probabilità di cadere in un punto dell’intervallo è uguale per tutti i punti dell’intervallo.

---

Sia $X=Unif([a,b])$ allora $P(X\subset [a,b])=1$, infatti $X$ ha sempre valori nell’intervallo essendo uniforme. Infatti:

$$P(X\in [a,b])={\int }_{[a,b]}f(x)dx={\int }_a^{b}f(x)dx={\int }_a^b\frac{1}{b-a}dx=1$$

Esercizio

Sia $X=Unif([2,8])$ calcolare $P(-3<X<4\text{ o }5\le X<8)$, noi sappiamo calcolare $P(X\in A)={\int }_{A}f(x)dx$.

Per quale $A\subset \mathbb{R}$ possiamo scrivere l’evento $-3<X<4\text{ o }5\le X<8$ come $X\in A$.

Si, prendiamo $A=(-3,4)\cup [5,8)$.

Quindi calcoliamo:

$$\begin{array}{rl}P(-3<X<4\text{ o }5\le X<8)={\int }_{A}f(x)dx& ={\int }_{(-3,4)}f(x)dx+{\int }_{[5,8)}f(x)dx\\ & ={\int }_{-3}^{4}f(x)dx+{\int }_5^{8}f(x)dx\end{array}$$

Dove:

$$f(x)=\{\begin{array}{l}\frac{1}{b-a}\text{ se }x\in [a,b];\frac{1}{6}\text{ se }x\in [2,8]\\ 0\text{ altrimenti}\end{array}$$

Infati dato che è uniforme in 2,8 tutti i punti hanno la stessa probabilità di $\frac{1}{8-2}=\frac{1}{6}$. Quindi abbiamo una situazione simile:

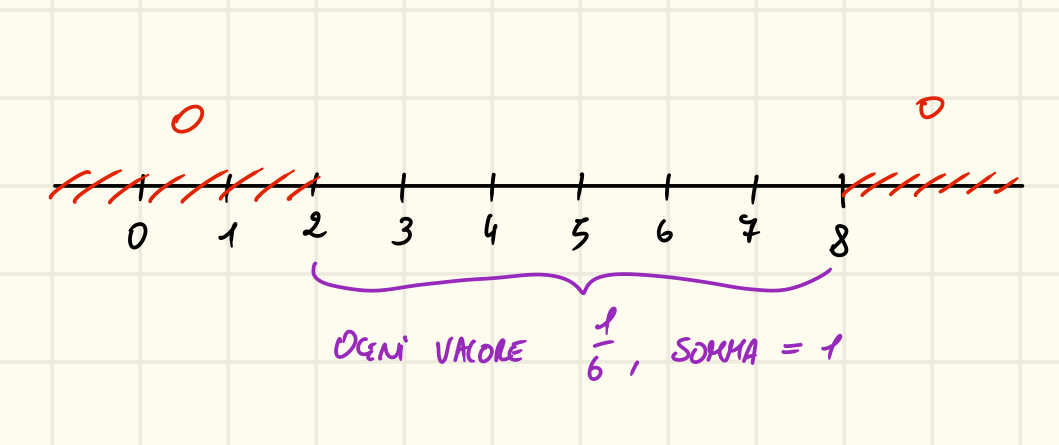
Eseguendo i calcoli otteniamo:

$$\begin{array}{rl}& {\int }_{-3}^{4}f(x)dx={\int }_2^{4}f(x)dx={\int }_2^4\frac{1}{6}dx=\frac{2}{6}\\ & \\ & {\int }_5^{8}f(x)dx={\int }_5^8\frac{1}{6}dx=\frac{3}{6}\\ & \\ & \text{Quindi in conclusione:}\\ & \\ & P(-3<X<4\text{ o }5\le X<8)=\frac{2}{6}+\frac{3}{6}=\frac{5}{6}\end{array}$$

Proposizione

Se $X$ è v.a. continua con funzione di densità $f$ allora:

$${\int }_{-\infty }^{+\infty }f(x)dx=1$$

---

$X$ è detta v.a. continua con funzione di densità $f\ge 0$ se $P(X\in A)={\int }_{A}f(x)dx$ $\forall A\subset \mathbb{R}$ (misurabile).

Ricordiamo che data $X$ v.a., la funzione di distribuzione (ripartizione) di $X$ è data da $F:\mathbb{R}\to [0,1]$ dove $F(x)=P(X\le x)$ $\forall x\in \mathbb{R}$.

Proposizione

Se $X$ è v.a. continua con funzione di densità $f$ allora:

$$F(x)={\int }_{-\infty }^{x}f(u)du$$

Infatti, $F(x)=P(X\le x)=P(X\in \underset{A}{\underbrace{(-\infty ,x]}})={\int }_{A}f(u)du=\underset{-\infty }{\overset{x}{\int }}f(u)du$

Proposizione

Sia $X$ v.a. continua allora $\forall x\in \mathbb{R}$ vale $P(X=x)=0$, infatti:

$$P(X=x)=P(X\in \{x\})={\int }_{\{x\}}f(u)du={\int }_x^{x}f(u)du=0$$

Anche nelle uniformi abbiamo questa regola, infatti è vero che la variabile assume valori nell’intervallo ma nessun valore dell’intervallo ha probabilità positiva. L’unica cosa che possiamo calcolare è la probabilità che la variabile assuma valori in degli intervalli.

Esercizio

Data $X$ v.a. continua con funzione di densità:

$$f(x)=\{\begin{array}{l}c{x}^2\text{ se }x\in [1,5]\\ 0\text{ altrimenti}\end{array}$$

• Calcolare $c$:

Sappiamo che ${\int }_{-\infty }^{\infty }f(x)dx=1$ quindi calcoliamo:

$$1={\int }_1^{5}c{x}^{2}dx=\frac{124}{3}c$$

Quindi $c=\frac{3}{124}$

• Calcolare $P(X>3)$

È la stessa cosa di calcolare $P(X\in (3,+\infty ))$ che, per come è definita la variabile, è uguale a $P(X\in (3,5])$:

$${\int }_3^{5}f(x)dx=\frac{3}{124}{\int }_3^5{x}^{2}dx=\frac{3}{124}\cdot \frac{5^3-3^3}{3}=\frac{98}{124}$$

Valore Atteso e Varianza di Variabili Aleatorie continue

Se $X$ è v.a. continua allora:

$$E[X]:={\int }_{-\infty }^{\infty }xf(x)dx$$

Non pensiamo che sia come il classico valore atteso ovvero $f(x)=P(X=x)$, l’interpretazione corretta è che:

$$f(x)dx=P(X\in [x,x+dx])+o(dx)$$

Ovvero la probabilità che $X$ sia in un intervallo molto piccolo intorno al valore $x$.

Per calcolarlo con delle funzioni, invece vale: Proposizione

Sia $X$ v.a. continua con funzione di densità $f$ e sia $g:\mathbb{R}\to \mathbb{R}$ allora:

$$E[g(X)]={\int }_{-\infty }^{\infty }g(x)f(x)dx$$

Per quanto riguarda la varianza invece se $X$ v.a. continua allora:

$$Var(X)=E[(X-EX{)}^2]$$

In generale per le v.a. continue valgono le stesse proprietà che abbiamo visto per le discrete.

Una proprietà aggiuntiva che invece troviamo nelle uniformi è la seguente:

Proprietà

Sia $X=Unif([a,b])$ e:

$$f(x)=\{\begin{array}{l}\frac{1}{b-a}\text{ se }x\in [a,b]\\ 0\text{ altrimenti}\end{array}$$

Allora:

$$E[X]=\frac{a+b}{2}$$

Infatti dato che la variabile è uniforme nell’intervallo, il valore atteso sarà proprio a metà intervallo.

Dimostrazione

$$\begin{array}{rl}EX={\int }_{-\infty }^{\infty }xf(x)dx={\int }_a^{b}x\frac{1}{b-a}dx=\frac{1}{b-a}{\int }_a^{b}xdx& =\frac{1}{b-a}\cdot \frac{x^2}{2}{|}_a^b\\ & =\frac{1}{b-a}\cdot \frac{b^2-a^2}{2}\\ & =\frac{1}{\cancel{b-a}}\cdot \frac{(b+a)\cancel{(b-a)}}{2}=\frac{a+b}{2}\end{array}$$

Proprietà

Per quanto riguarda la varianza, sempre nelle uniformi, vale invece:

$$Var(X)=\frac{(b-a{)}^2}{12}$$

Dimostrazione

$$Var(X)=E[X^2]-(EX{)}^2=E[X^2]-(\frac{a+b}{2}{)}^2$$

Calcoliamo singolarmente $E[X^2]$:

$$\begin{array}{rl}E[X^2]={\int }_{-\infty }^{\infty }{x}^{2}f(x)dx={\int }_a^b{x}^2\frac{1}{b-a}dx=\frac{1}{b-a}{\int }_a^b{x}^{2}dx& =\frac{1}{b-a}\cdot \frac{x^3}{3}{|}_a^b\\ & =\frac{1}{b-a}\cdot \frac{b^3-a^3}{3}=\frac{b^2+ab+a^2}{3}\end{array}$$

Adesso torniamo alla formula della varianza e mettendo insieme i risultati:

$$\begin{array}{rl}Var(X)=\frac{b^2+ab+a^2}{3}-\frac{a^2+2ab+b^2}{4}& =\frac{4b^2+4ab+4a^2-3a^2-6ab-3b^2}{12}\\ & =\frac{a^2-2ab+b^2}{12}=\frac{(b-a{)}^2}{12}\end{array}$$

Variabile Aleatoria Gaussiana

Una variabile aleatoria $X$ è detta gaussiana o normale di media $\mu \in \mathbb{R}$ e varianza ${\sigma }^2>0$ se è una v.a. continua con funzione di densità:

$$f(x)=\frac{1}{\sqrt{2\pi }\cdot \sigma }\cdot e^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$$

E scriveremo $X=\mathcal{N}(\mu ,{\sigma }^2)$

Gaussiana Standard

Se $\mu =0$ e ${\sigma }^2=1$ allora $X=\mathcal{N}(0,1)$ è detta Guassiana Standard, quindi:

$$f(x)=\frac{1}{\sqrt{2\pi }}\cdot e^{-\frac{x^2}{2}}$$

---

I nomi dei parametri non sono casuali, infatti possiamo provare che $E[X]=\mu$ e che $Var(X)={\sigma }^2$, infatti anche la deviazione quadratica standard è uguale a:

$$\sigma =\sqrt{{\sigma }^2}=\sqrt{Var(X)}$$

Il grafico di una Gaussiana è a campana e simmetrico rispetto alla retta verticale $x=\mu$, inoltre $\forall x$ $f(x)>0$ ma quasi tutta l’area della campana è concentrata in:

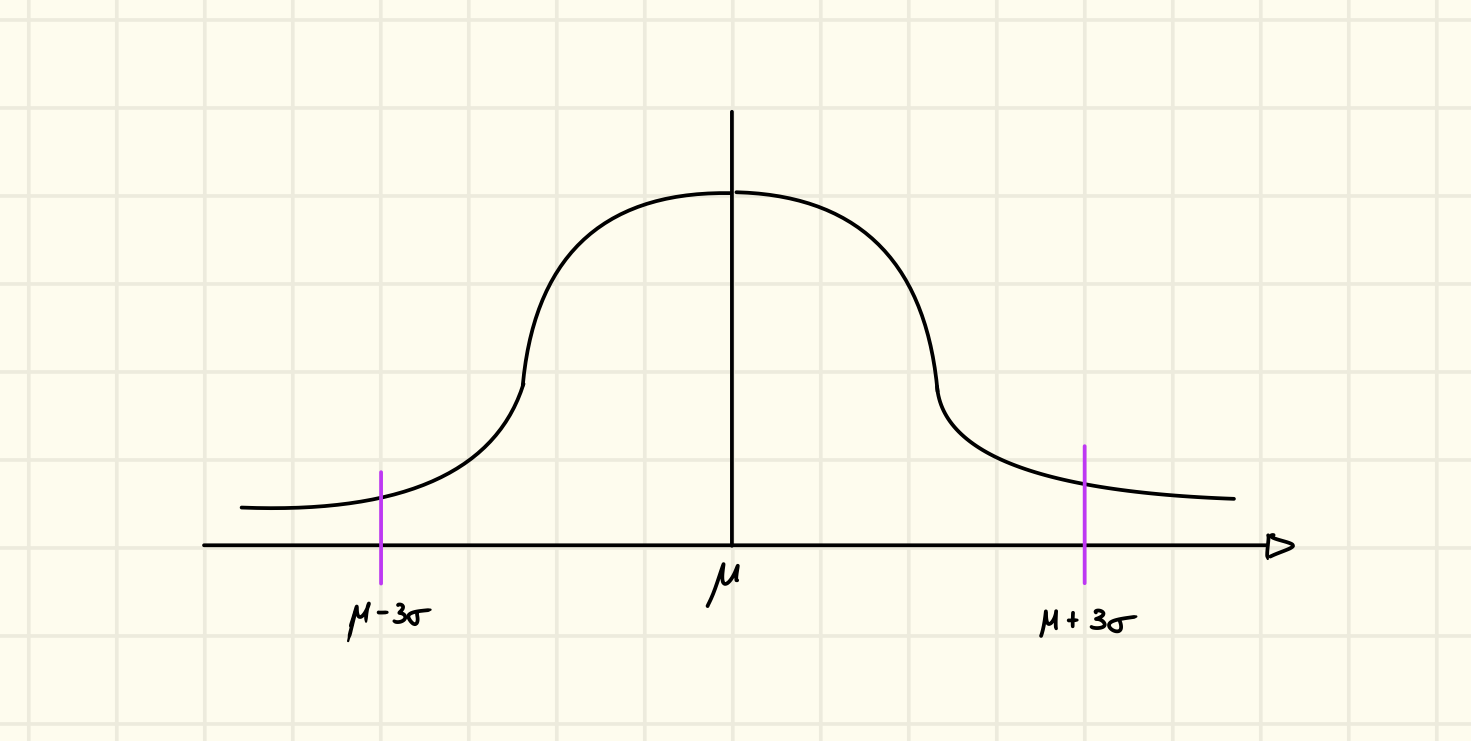
Attenzione

La variabile Gaussiana è ben definita, ovvero esiste, perché $f\ge 0$ e $1={\int }_{-\infty }^{\infty }f(x)dx$, infatti data in generale una $f:\mathbb{R}\to [0,+\infty )$ con $1={\int }_{-\infty }^{\infty }f(x)dx$ si può sempre costruire una v.a. $X$ continua che ha $f$ come funzione di densità.

Funzione di distribuzione

Sia $X=\mathcal{N}(\mu ,{\sigma }^2)$ calcoliamo $F(x)$ ovvero $P(X\le x)$:

$$P(X\le x)={\int }_{-\infty }^{x}f(z)dz=\frac{1}{\sqrt{2\pi }\cdot \sigma }{\int }_{-\infty }^x{e}^{-\frac{(z-\mu {)}^2}{2{\sigma }^2}}dz$$

Se $X$ è una gaussiana standard e quindi $N(0,1)$ invece di scrivere $F(x)$ scriviamo $\varphi (x)$:

$$\varphi (x)=\frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^x{e}^{-\frac{z^2}{2}}dz$$

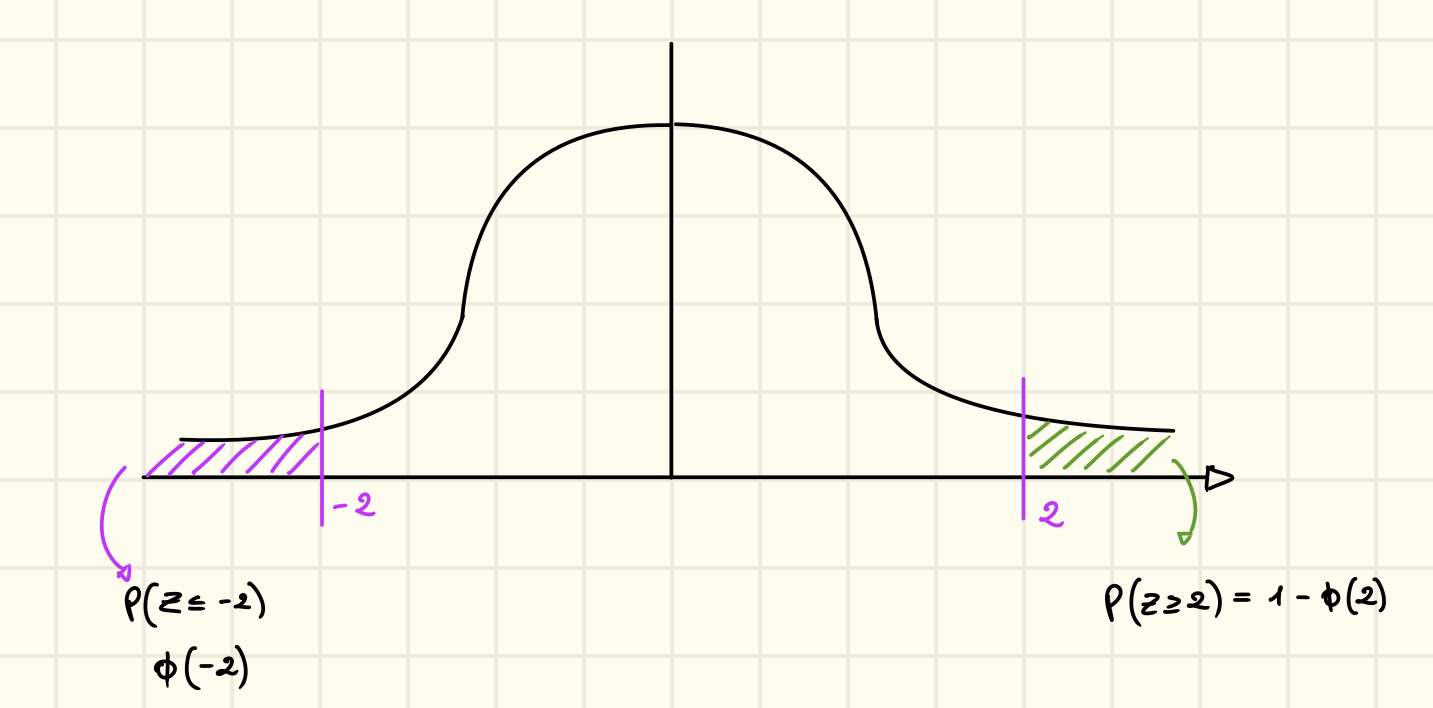
Per $\varphi (x)$ troviamo delle tabelle già compilate con $x\ge 0$, perché non troviamo i valori negativi? Osserviamo graficamente cosa otteniamo con $\varphi (x)$:

Prendiamo ad esempio $\varphi (3)$ (non ci interessa il risultato ma solo il grafico):

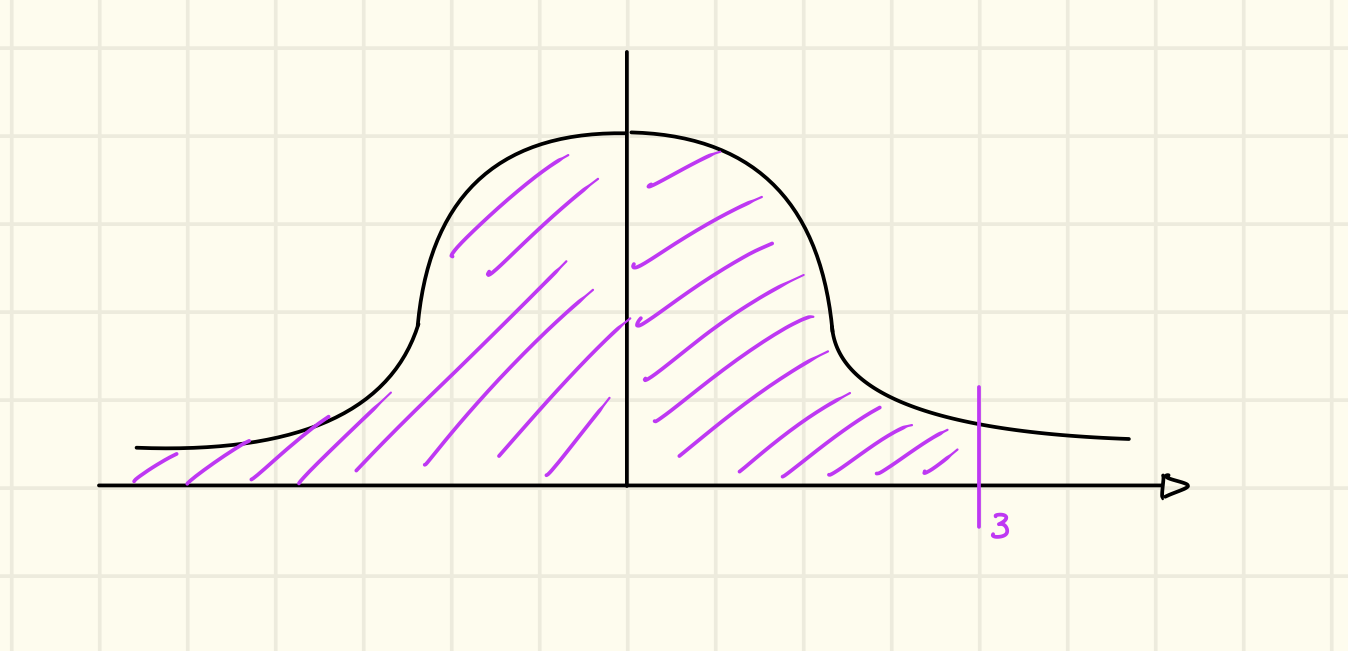
Stiamo calcolando l’area colorata di viola, adesso guardiamo ad esempio, a cosa corrisponde graficamente $\varphi (-3)$:

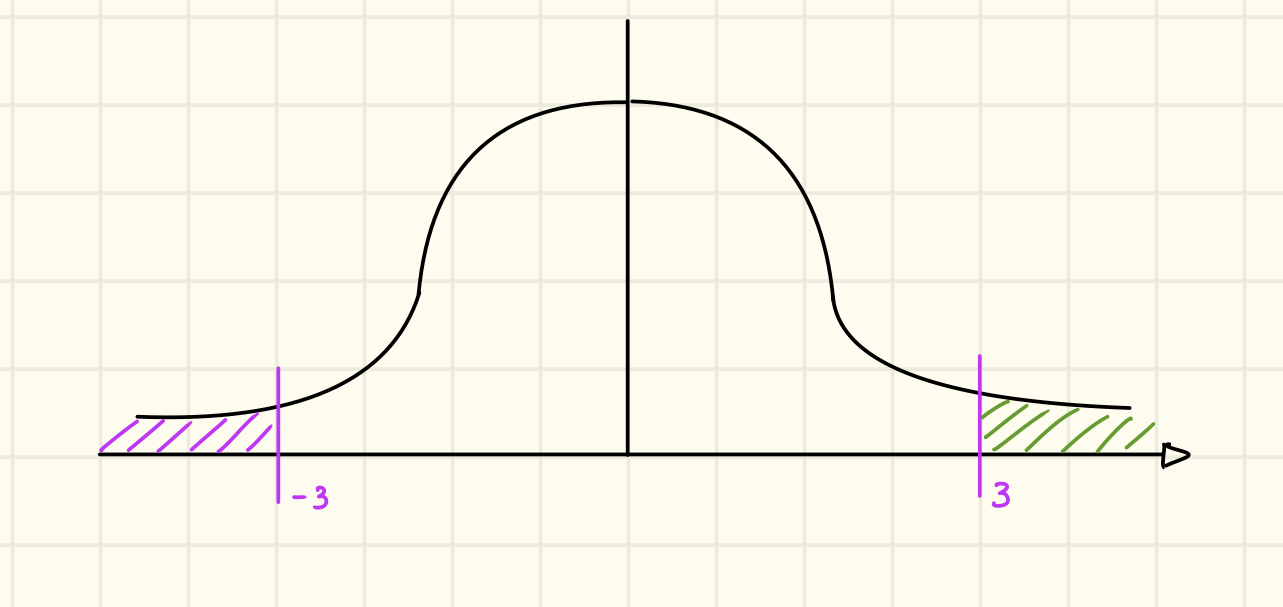
$\varphi (-3)$ corrisponde all’area colorata di viola, ma notiamo che è identica all’area verde che prima abbiamo escluso con $\varphi (3)$, cosa significa questo? Che $\varphi (-3)=1-\varphi (3)$. Quindi i valori negativi non sono presenti nella tabella perché possiamo calcolarli tramite i loro valori inversi.

In generale quindi $\varphi (-x)=1-\varphi (x)$, e inoltre $\varphi (0)=\frac{1}{2}$

Prendiamo ad esempio $Z=\mathcal{N}(0,1)$ e calcoliamo $P(|Z|\ge 2)$ questo corrisponde a calcolare $P(Z\le 2\text{ o }Z\ge 2)$:

$$=\underset{\varphi (-2)=1-\varphi (2)}{\underbrace{P(Z\le -2)}}+\underset{1-\varphi (2)=\varphi (-2)}{\underbrace{P(Z\ge 2)}}=2(1-\varphi (2))=2\cdot 0.0228=0.0456=4.56\%$$

In generale possiamo dire $\varphi (x)=P(Z\le x)$, per vedere meglio i calcoli sopra vediamo il grafico:

Proposizione

Sia $\mu \in \mathbb{R}$ e ${\sigma }^2>0$ e sia $Z=\mathcal{N}(0,1)$ allora $Y:=\pm \sigma Z+\mu$ è $\mathcal{N}(\mu ,{\sigma }^2)$

Dove possiamo calcolare:

• $E[Y]=E[\sigma Z+\mu ]=\sigma E[Z]+\mu =\sigma \cdot 0+\mu =\mu$
• $Var(Y)=Var(\sigma Z+\mu )={\sigma }^{2}Z\cdot Var(Z)={\sigma }^2\cdot 1={\sigma }^2$

Dimostrazione

Devo capirla =P perché pisciato lezione.

Possiamo anche dimostrare che $Y=\mathcal{N}(\mu ,{\sigma }^2)\Rightarrow \frac{Y-\mu }{\sigma }=\mathcal{N}(0,1)$

Esercizio

Sia $Y=\mathcal{N}(3,16)$, usando $\varphi$ calcolare $P(Y\ge 10)$

$$P(Y\ge 10)=P(Y-3\ge 10-3)=P\left(\frac{Y-3}{4}\ge \frac{10-3}{4}\right)$$

In questo modo possiamo definire $Z=\frac{Y-3}{4}=\mathcal{N}(0,1)$ dato che $\mu =3$ e $\sigma =4({\sigma }^2=16)$ e quindi calcolare adesso:

$$P\left(Z\ge \frac{7}{4}\right)=P(Z\ge 1.75)=1-\varphi (1.75)=1-0.9599=0.0401$$

---

Variabili Aleatorie Identicamente Distribuite

Adesso vediamo due casi di variabili aleatorie diverse ma “con le stesse caratteristiche”:

Caso 1

Abbiamo un mazzo da 40 carte, estraiamo una carta e definiamo:

$$X=\{\begin{array}{l}1\text{ se ho estratto Bastoni o Coppe}\\ 0\text{ altrimenti}\end{array}$$

Come spazio campionario abbiamo il mazzo di carte e quindi esiti equiprobabili, quindi calcoliamo:

$$P(X=1)=\frac{1}{2}P(X=0)=\frac{1}{2}$$

Caso 2

Lanciamo una moneta e definiamo:

$$Y=\{\begin{array}{l}1\text{ se esce T}\\ 0\text{ se esce C}\end{array}$$

Come spazio campionario abbiamo quindi $S=\{T,C\}$ e calcoliamo:

$$P(Y=1)=\frac{1}{2}P(Y=0)=\frac{1}{2}$$

Notiamo che $X,Y$ sono v.a. distinte e anche con funzioni definite anche su spazi campionari diversi, nonostante questo assumono gli stessi valori con le stesse probabilità.

Definizione

Date v.a. $X:S\to \mathbb{R}$ e $Y:S^{\prime }\to \mathbb{R}$, $X,Y$ sono dette identicamente distribuite (o aventi la stessa legge) se:

$$P(X\in A)=P(Y\in A)\forall A\subset \mathbb{R}$$

Osservazione

Se $X$ è v.a. discreta che assume valori $\{x_i{\}}_{i\in I}$ allora $P(X\in A)=P(X\in A\cap \{x_i{\}}_{i\in I})$ che è uguale a:

$$P\left(\bigcup _{i:x_i\in A}\{X=x_i\}\right)=\sum _{i:x_i\in A}P(X=x_i)=\sum _{i:x_i\in A}{p}_X(x_i)=\sum _{x\in A}{p}_X(x)$$

In conclusione quindi $P(X\in A)=\sum _{x\in A}{p}_X(x)$

Siano adesso $X$ e $Y$ v.a. discrete e supponiamo che $p_X=p_Y$. Allora per quanto appena provato possiamo dire che:

$$P(X\in A)=\sum _{x\in A}{p}_X(x)\underset{p_X=p_Y}{=}\sum _{x\in A}{p}_Y(x)=P(Y\in A)$$

Abbiamo provato quindi che due v.a. discrete $X,Y$ con $p_X=p_Y$ sono identicamente distribuite e si può provare anche il viceversa, quindi:

Proposizione

Siano $X,Y$ v.a. discrete allora $X,Y$ sono identicamente distribuite(I.D.) $\iff p_X=p_Y$

Per le v.a. continue vale qualcosa di simile:

Proposizione

Siano $X,Y$ v.a. continue (anche con spazi campionari diversi) chiamiamo $f_X$ e $f_Y$ le rispettive funzioni di densità di probabilità. Allora:

$$X,Y\text{ sono I.D.}\iff f_X=f_Y\text{ ovunque (o quasi)}$$

Dimostriamo quindi che se $X,Y$ sono continue e $f_X=f_Y$ allora sono I.D.

Fissato un $A\subset \mathbb{R}$ abbiamo che:

$$P(X\in A)={\int }_A{f}_X(x)dx\underset{f_X=f_Y}{=}{\int }_A{f}_Y(x)dx=P(Y\in A)$$

Dove ovviamente nella $f_Y$ le $x$ sono equivalenti alle $y$ dato che la funzione di distribuzione di è identica.

Abbiamo provato quindi che $P(X\in A)=P(Y\in A)$ $\forall A\subset \mathbb{R}$ e quindi $X,Y$ sono I.D.

Teorema di De Moivre - Laplace (preludio del teorema del limite centrale)

Fissiamo $p\in (0,1)$. Dato $n\in \{1,2,3,\dots \}$ sia $S_n$ v.a. binomiale di parametri $n,p$. Sia $Z=\mathcal{N}(0,1)$ allora $\forall a<b$ vale:

$$\underset{n\to \infty }{\lim }P\left(a\le \frac{S_n-np}{\sqrt{np(1-p)}}\le b\right)=P(a\le Z\le b)$$

Inoltre $\frac{S_n-np}{\sqrt{np(1-p)}}$ ha valore atteso 0 e varianza 1.

Dimostriamolo usando che $E[S_n]=np$ e che $Var(S_n)=np(1-p)$:

$$\begin{array}{rl}& E\left[\frac{S_n-np}{\sqrt{np(1-p)}}\right]\underset{\text{linearitaˋ di E}}{=}\frac{E[S_n]-np}{\sqrt{np(1-p)}}=\frac{np-np}{\sqrt{np(1-p)}}=0\\ & \\ & Var\left(\frac{S_n-np}{\sqrt{np(1-p)}}\right)=Var\left(\frac{S_n}{\sqrt{np(1-p)}}\right)=\frac{1}{np(1-p)}\cdot Var(S_n)=\frac{np(1-p)}{np(1-p)}=1\end{array}$$

Inoltre $S_n=X_1+X_2+\cdots +X_n$ che sono tutte indipendenti quindi sono tutte $Bern(p)$. $S_n$ è quindi somma di v.a. indipendenti identicamente distribuite.

Teorema del Limite Centrale

Nel teorema di De Moivre consideriamo $S_n=Bin(n,p)$ che non è altro che la somma di $n$ v.a. indipendenti di prove successo / insuccesso con $p$ probabilità di successo per ogni singola prova.

Quindi definiamo $S_n$ come il numero di successi e notiamo che:

$$S_n=X_1+X_2+\cdots +X_n$$

Dove:

$$X_i=\{\begin{array}{l}1\text{ se alla prova i ho successo}\\ 0\text{ altrimenti}\end{array}$$

Per $i=1,2,\dots ,n$ abbiamo che $X_1,\dots ,X_n$ sono tutte $Bern(p)$ quindi identicamente distribuite e sono v.a. indipendenti perché si riferiscono a prove indipendenti.

L’importante è quindi che $S_n$ è somma di $n$ v.a. I.I.D. (indipendenti e identicamente distribuite)

Enunciato Teorema Limite Centrale

Siano $X_1,X_2,X_3,\dots$ v.a. indipendenti e identicamente distribuite, tutte di valore atteso $\mu \in \mathbb{R}$ e di varianza ${\sigma }^2\in (0,\infty )$ allora posto $S_n:=X_1+\dots X_n$ abbiamo:

$$\frac{S_n-n\mu }{\sigma \sqrt{n}}\to Z=\mathcal{N}(0,1)$$

Più precisamente, $\forall a<b$ vale:

$$\underset{n\to \infty }{\lim }P\left(a<\frac{S_n-\mu n}{\sigma \sqrt{n}}<b\right)=\underset{\frac{1}{\sqrt{2\pi }}{\int }_a^b{e}^{-\frac{x^2}{2}}dx}{\underbrace{P(a<Z<b)}}$$

Commenti sul Teorema

$X_1,X_2,\dots ,X_n$ sono v.a. I.I.D., cosa significa?

• Indipendenti significa che $\forall n$ $X_1,\dots ,X_n$ sono indipendenti, ovvero:

$$P(X_1\in A_1,\dots ,X_n\in A_n=\prod _{i=1}^{n}P(X_i\in A_i)\forall A_1,\dots ,A_n\subset \mathbb{R}$$

• Identicamente Distribuite significa che $\forall i\ne j$ vale $P(X_i\in A)=P(X_j\in A)\forall A\subset \mathbb{R}$, quindi non le distinguiamo a livello probabilistico.

• Per v.a. discrete questo significa che $p_{X_i}=p_{X_j}$ $\forall i\ne j$, mentre per v.a. continue questo significa che $f_{X_i}=f_{X_j}$ $\forall i\ne j$

Prendiamo un esempio di successione IID: $X_1,X_2,\dots$ sono tutte indipendenti e $Bern(p)$ allora in questo caso $S_n=X_1+\cdots +X_n=Bin(n,p)$ e infatti il Teorema di De Moivre non è altro che un caso particolare del Teorema del Limite Centrale.

Infatti abbiamo detto che $X_1,\dots$ è una successione di v.a. indipendenti $Bern(p)$, allora $\mu =E[X_i]=p$ e ${\sigma }^2=Var(X_i)=p(1-p)$.

Otteniamo quindi che:

• $n\mu =np$
• $\sigma \sqrt{n}=\sqrt{{\sigma }^{2}n}=\sqrt{np(1-p)}$

E il TLC mi diche che posto $S_n=X_1+\cdots +X_n=Bin(n,p)$ si ha:

$$\frac{S_n-n\mu }{\sigma \sqrt{n}}=\frac{S_n-np}{\sqrt{np(1-p)}}\to Z=\mathcal{N}(0,1)$$

Che non è altro che il Teorema di De Moivre

---

Esistono v.a. per cui valore atteso o varianza non son ben definite oppure sono ben definite ma divergono, nel T.L.C (Teorema Limite Centrale) queste situazioni non sono considerate, infatti abbiamo che $\mu \in \mathbb{R}$ e che ${\sigma }^2\in (0,+\infty )$.

---

Nel TLC consideriamo la v.a. $\frac{S_n-\mu n}{\sigma \sqrt{n}}$ ma da dove vengono $n\mu$ e $\sigma \sqrt{n}$ ?

$$\begin{array}{rl}& E[S_n]=E[X_1+\cdots +X_n]=E[X_1]+\cdots +E[X_n]=n\mu \\ & \\ & \text{Abbiamo trovato quindi che }E[S_n]=n\mu ,\text{ quindi}:\\ & \\ & E\left[\frac{S_n-n\mu }{\sigma \sqrt{n}}\right]=\frac{E[S_n]-n\mu }{\sigma \sqrt{n}}=0\end{array}$$

Mentre per quanto riguarda la varianza:

$$\begin{array}{rl}& Var(S_n)=Var(X_1+\cdots +X_n)=\sum _{i=1}^{n}Var(X_i)=n{\sigma }^2\\ & \\ & \text{Quindi:}\\ & \\ & Var\left(\frac{S_n-n\mu }{\sigma \sqrt{n}}\right)=Var\left(\frac{1}{\sigma \sqrt{n}}{S}_n-\frac{n\mu }{\sigma \sqrt{n}}\right)={\left(\frac{1}{\sigma \sqrt{n}}\right)}^{2}Var(S_n)=\frac{1}{{\sigma }^{2}n}\cdot n{\sigma }^2=1\end{array}$$

• Quindi le costanti che appaiono in $\frac{S_n-n\mu }{\sigma \sqrt{n}}$ sono state scelte per garantire che il suo valore atteso sia 0 e la varianza 1

Legge Forte dei Grandi Numeri

Inizialmente nel corso ci ponevamo domande del tipo “Cosa significa che lanciando una moneta abbiamo 1/3 di probabilità che esca testa?“. Una prima risposta era che “Lanciando una moneta tante volte allora esce testa in circa un terzo dei casi” ma non riuscivamo a rendere precisa questa affermazione che ha varie criticità, ad esempio non possiamo definire il circa o le tante volte.

Abbiamo quindi scartato questa opzione e abbiamo introdotto lo spazio di probabilità come modello matematico astratto.

Ma esiste un teorema che ci permette di non scartare completamente la prima idea? Si, la legge forte dei grandi numeri.

Consideriamo un esperimento descritto dallo spazio di probabilità (S,P).

Esempio

Lancio una moneta truccata che dà T con prob 1/3. Abbiamo quindi che $S=\{T,C\}$ e $P(\{T\})=\frac{1}{3}$ mentre $P(\{C\})=\frac{2}{3}$.

Introduciamo un META-esperimento come segue: Ripeto l’esperimento descritto da (S,P) infinite volte sempre con lo stesso protocollo e gli esperimenti che ripeto non si influenzano, sono quindi indipendenti fra loro.

Il Meta-esperimento è descritto dal suo spazio di probabilità che denotiamo con $(\overline{S},\overline{P})$, $\overline{S}$ é dato quindi da: $\overline{S}=\{(s_1,s_2,\dots ):s_i\in S\}$ e quindi tornando all’esempio della moneta abbiamo che $\overline{S}=\{(s_1,s_2,\dots ):s_i\in \{T,C\}\}$, quindi $s_i$ é l’esito di un sottoesperimento, notiamo quindi che l’esito del meta-esperimento é una stringa composta dagli esiti dei sottoesperimenti, ad esempio:

$(T,C,T,T,C,C,\dots )$ significa che al primo lancio abbiamo ottenuto testa, al seconda croce, al terzo testa…

Per quanto riguarda la funzione di probabilità $\overline{P}$ la situazione è più complessa e difficile da introdurre.

Questa si chiama probabilità prodotto e la indichiamo con $\overline{P}$, questa funzione di probabilità ha le seguenti proprietà:

• $\overline{P}=(\{\overline{s}=(s_1,\dots )\in \overline{S}:s_i\in E\})=P(E)$ questo $\forall i\in \{1,2,\dots \}={\mathbb{N}}_{+}$ e $\forall E\subset S$
• $\overline{P}(E_1\times E_2\times \cdots \times E_n\times S\times S\times \dots )=P(E_1)P(E_2)\dots P(E_n)$ questo $\forall n$ e $\forall E_1,E_2,\dots ,E_n\subset S$

Possiamo spiegare queste proprietà in modo più discorsivo:

• $\overline{P}$ ha la proprietà che se mi interesso alla prova i-esima la probabilità che il risultato della prova i-esima soddisfi l’evento $E\subset S$ è la probabilità che si verifichi $E$ nell’esperimento base (ad esempio la probabilità che al terzo lancio di un dado esca 2 é 1/6 proprio come nell’esperimento base)
• $\overline{P}$ ha la proprietà che eventi riferiti a prove diverse sono indipendenti

Frequenza Assoluta

Osserviamo che il metaesperimento é descritto dallo spazio di probabilità $(\overline{S},\overline{P})$ dove $\overline{S}=S^{{\mathbb{N}}_{+}}$ con ${\mathbb{N}}_{+}=\{1,2,\dots \}$. Quindi $\overline{S}=\{(s_1,\dots ):s_i\in S\forall i\in {\mathbb{N}}_{+}\}$.

Fissiamo adesso un evento $E\subset S$ ad esempio $E=\text{Esce un numero pari}$ e dato un $n$ intero definiamo:

$$Y_n^E:=\text{Volte in cui si verifica E nelle prime n prove del metaesperimento}$$

È quindi una funzione definita su:

$$Y_n^E:\overline{S}\to \{0,1,2,\dots ,n\}$$

Esempio

Supponiamo $\overline{s}=(4,3,2,5,1,1,\dots )$ (ricordiamo che è infinito) e se $E=\{2,4,6\}$ allora:

$$\begin{array}{r}{Y}_3^E(\overline{s})=2\\ Y_6^E(\overline{s})=2\end{array}$$

Teorema (Interpretazione frequentistica della probabilità)

$\forall E\subset S$ evento dell’esperimento base, vale:

$$\overline{P}\left(\left\{\overline{s}:\underset{n\to \infty }{\lim }\frac{Y_n^E(\overline{s})}{n}=P(E)\right\}\right)=1$$

• $\frac{Y_n^E(\overline{s})}{n}$ Questo prende il nome di frequenza relativa di E nelle prime n prove

Questa formula è conseguenza della legge forte dei grandi numeri e risolve i problemi che avevamo per rispondere alla domanda sulla probabilità. Infatti con “tanti lanci” ci riferiamo alla probabilità del metaesperimento $\overline{P}$ mentre con $P$ ci riferiamo alla probabilità del singolo lancio. Inoltre abbiamo una definizione precisa ovvero $=1$ e non “circa”.

Teorema (Legge Forte dei Grandi Numeri)

Sia $(S,P)$ spazio di probabilità e siano $X_1,X_2,\dots$ v.a. IID tutte definite su $S$ e con valore atteso $\mu$. Allora:

$$P\left(\left\{s\in S:\underset{n\to \infty }{\lim }\frac{X_1(s)+X_2(s)+\cdots +X_n(s)}{n}=\mu \right\}\right)=1$$

Ricordiamo infatti che IID sta per indipendenti e identicamente distribuite e che per identicamente distribuite intendiamo:

$$P(X_i\in A)=P(X_j\in A)\forall i\ne j\forall A\subset \mathbb{R}$$

E questo implica che:

$$E[X_i]=E[X_j]$$

Quindi in modo discorsivo possiamo dire che, la media aritmetica di una sequenza di variabili aleatorie IID converge al loro valore atteso quando il numero di esperimenti tende a infinito.

Corollario della Legge forte dei grandi numeri

$\forall (S,P)$ prendiamo un esperimento base e $\forall X:S\to \mathbb{R}$ variabile aleatoria con $\mu :E[X]$ ben definito, vale:

$$\overline{P}\left(\left\{\overline{s}\in \overline{S}:\underset{n\to \infty }{\lim }\frac{X_1(\overline{s})+\cdots +X_n(\overline{s})}{n}=E[X]\right\}\right)=1$$

Questo ci dà un’interpretazione frequentistica del valore atteso.

Ricordando che definiamo $\forall i=1,2,\dots$ $X_i:\overline{S}\to \mathbb{R}$ come:

$$X_i(\overline{s})=X(s_i)$$

Dove $\overline{s}=(s_1,s_2,\dots )\in \overline{S}$