BD1 - Ripasso Orale - 3NF

Praticamente quello che sta nelle dispense ma ho bisogno di scrivere le cose per studiarle, poi boh aggiungerò qualcosa sulle dimostrazioni.

---

3NF

Nelle basi di dati voglia evitare 3 situazioni:

• Anomalie di Inserimento: Vogliamo inserire un dato ma per farlo dobbiamo inserirne anche altri
• Anomalie di Cancellazione: Come l’inserimento quindi vogliamo cancellare un dato ma per farlo ne perdiamo anche altri
• Anomalie di Aggiornamento: Se vogliamo aggiornare un dato dobbiamo farlo in ogni tupla dove compare
• Ridondanza nella rappresentazione dei dati

Definizione 1: Dato uno schema di relazione $R$, una dipendenza funzionale su $R$ è una coppia ordinati di sottoinsiemi non vuoti $X,Y$ di $R$ e viene denotata con $X\to Y$.

Si dice che un’istanza $r$ di $R$ soddisfa la dipendenza funzionale $X\to Y$ se per ogni coppia di tuple $t_1,t_2$ si ha che se $t_1[X]=t_2[X]$ allora $t_1[Y]=t_2[Y]$.

Se $F$ è un insieme di dipendenze funzionali su $R$ ed $r$ è un’istanza di $R$ che soddisfa tutte le dipendenze di $F$, diciamo che $r$ è un’istanza legale di $R$.

La chiusura di $F$ denotata con $F^{+}$ è l’insieme di dipendenze funzionali che sono soddisfatte da ogni istanza legale di $R$.

Banalmente si ha che $F\subseteq F^{+}$.

Definizione 2: Dato uno schema di relazione $R$, un insieme di dipendenze funzionali $F$ su $R$ e un sottoinsieme $K$ di $R$ diciamo che $K$ è una chiave per $R$ se:

• $K\to R\in F^{+}$
• Per ogni sottoinsieme proprio $K^{\prime }$ di $K$ si ha che $K^{\prime }\to R\notin F^{+}$ (quindi non devono esserci sottoinsiemi che sono chiave a loro volta)

Info su 3NF

Uno schema di relazione in cui non ci sono attributi che dipendono parzialmente né transitivamente dalla chiave è detto in terza forma normale.

Più formalmente:

Definizione 3: Dati uno schema di relazione $R$ e un insieme di dipendenze funzionali $F$ su $R$ diciamo che:

• Un attributo $A$ di $R$ è primo se appartiene ad una chiave di $R$
• Un sottoinsieme $X$ di $R$ è una superchiave se contiene una chiave di $R$

Definizione 4: Siano $R$ uno schema di relazione e $F$ un insieme di dipendenze funzionali su $R$:

• $X\to A\in F^{+}$ tale che $A\notin X$ è una dipendenza parziale su $R$ se $A$ non è primo ed $X$ è contenuto propriamente in una chiave di $R$. In modo discorsivo non abbiamo dipendenze parziali se gli attributi che non appartengono alla chiave devono dipendere dall’intera chiave

• $X\to A\in F^{+}$ tale che $A\notin X$ è una dipendenza transitiva su $R$ se $A$ non è primo e per ogni chiave $K$ di $R$ si ha che $X$ non è contenuto propriamente in $K$ e $K-X\ne \varnothing$. Non abbiamo dipendenze transitive se gli attributi che non appartengono alla chiave, dipendono direttamente dalla chiave e non da altri attributi non chiave.

  

Definizione 5: Siano $R$ uno schema di relazione e $F$ un insieme di dipendenze funzionali su $R$. $R$ è in 3NF se per ogni dipendenza funzionale $X\to A\in F^{+}$ tale che $A\notin X$ si ha che:

• $A$ è primo, oppure
• $X$ è una superchiave.

Teorema 1: Siano $R$ uno schema di relazione e $F$ un insieme di dipendenze funzionali su $R$. Uno schema $R$ è in 3NF se e solo se non esistono né dipendenze parziali né dipendenze transitive in $R$.

Dimostrazione

• Parte SOLO SE: Se non abbiamo dipendenze parziali e transitive, tutte le nostre dipendenze $X\to A$ avranno $X$ chiave o che ne contiene una e quindi verificano sempre la condizione vista prima $X$ superchiave.

• Parte SE: Lo schema $R$ è in 3NF quindi $\forall X\to A\in F^{+},A\notin X$ abbiamo che $A$ primo oppure $X$ superchiave, quindi ci sono diversi casi:

1. Se $A$ è primo viene a mancare la condizione per avere dipendenze parziali e transitive, quindi abbiamo terminato
2. Se $A$ non è primo allora $X$ è superchiave per l’altra condizione, in quanto tale può contenere una chiave ma non essere contenuto propriamente e quindi non possiamo avere dipendenze parziali (dove la chiave deve contenere propriamente X). Inoltre essendo superchiave non possono verificarsi, per ogni chiave, le condizioni di dipendenza transitive dato che almeno una è contenuta in $X$.

Abbiamo quindi dimostrato che le due condizioni di 3NF sono equivalenti.

Decomposizioni che preservano le dipendenze.

Quando si decompone uno schema è importante che questa decomposizioni preservi tutte le dipendenze presenti in $F^{+}$ ovvero la chiusura di $F$. Come si calcola questo insieme? Introduciamo un altro insieme $F^A$.

Sia $R$ uno schema di relazione e $F$ un insieme di dipendenze funzionali, sia $F^A$ l’insieme di dipendenze funzionali definito nel modo seguente:

• se $f\in F$ allora $f\in F^A$
• se $Y\subseteq X\subseteq R$ allora $X\to Y\in F^A$ riflessivitá
• se $X\to Y\in F^A$ allora $XZ\to YZ\in F^A$ per ogni $Z\subseteq R$ aumento
• se $X\to Y\in F^A$ e $Y\to Z\in F^A$ allora $X\to Z\in F^A$ transitività

Dimostreremo che $F^{+}=F^A$ ovvero che la chiusura di insieme di dipendenze può essere ottenuta applicando ricorsivamente gli assiomi di Armstrong, sono utili inoltre altre regole utile che ci permettono di ricavare da delle dipendenze in $F^A$ altre dipendenze di $F^A$:

• se $X\to Y\in F^A$ e $X\to Z\in F^A$ allora $X\to YZ\in F^A$ unione
• se $X\to Y\in F^A$ e $Z\subseteq Y$ allora $X\to Z\in F^A$ decomposizione
• se $X\to Y\in F^A$ e $WY\to Z\in F^A$ allora $WX\to Z\in F^A$ pseudotransitività

Teorema 2: Sia $F$ un insieme di dipendenze funzionali, valgono le 3 regole viste sopra.

Dimostrazione

• Unione: Se $X\to Y\in F^A$, per l’aumento si ha che $X\to XY\in F^A$. Analogamente se $X\to Z\in F^A$ sempre per aumento si ha che $XY\to YZ\in F^A$ quindi dato che abbiamo $X\to XY;XY\to YZ\in F^A$ per transitività possiamo dire che $X\to YZ\in F^A$.

• Decomposizione: Se $Z\subseteq Y$ allora per riflessività si ha che $Y\to Z\in F^A$ quindi poiché $X\to Y\in F^A$ e $Y\to Z\in F^A$ per transitività abbiamo che $X\to Z\in F^A$.

• Pseudotransitività: Se $X\to Y\in F^A$, per l’aumento possiamo dire che $WX\to WY\in F^A$ quindi poiché $WX\to WY\in F^A$ e $WY\to Z\in F^A$ per transitività abbiamo che $WX\to Z\in F^A$.

Definizione 6: Siano $R$ uno schema di relazione, $F$ un insieme di dipendenze funzionali su $R$ e $X$ un sottoinsieme di $R$. La chiusura di $X$ rispetto ad $F$ denotata con $X_F^{+}$ è definito come $X_F^{+}=\{A:X\to A\in F^A\}$

Lemma 1: Siano $R$ uno schema di relazione ed $F$ un insieme di dipendenze funzionali su $R$. Si ha che $X\to Y\in F^A$ se e solo se $Y\subseteq X^{+}$.

Dimostrazione: Sia $Y=A_1,A_2,\dots ,A_n$.

• Parte SE: Poiché $X\to Y\in F^A$, per la decomposizione possiamo dire che $\forall i=1,\dots ,n$ si ha che $X\to A_i\in F^A$ e questo significa che $A_i\in X_{+}$. Dove $A_i$ per ogni $i$ sono gli attributi presenti in $Y$ e quindi $Y\subseteq X^{+}$.

• Parte SOLO SE: Dato che $Y\subseteq X^{+}$, per ogni $i=1,\dots ,n$ si ha che $X\to A_i\in F^A$ pertanto per l’unione $X\to Y\in F^A$.

Teorema 3: Siano $R$ uno schema di relazione ed $F$ un insieme di dipendenze funzionali su $R$ si ha $F^{+}=F^A$.

Dimostrazione

• Dimostriamo che $F^A\subseteq F^{+}$

Sia $X\to Y$ una dipendenza funzionale in $F^A$ dimostriamo per induzione sul numero $i$ di applicazioni di uno degli assiomi di Armstrong.

Base Induzione: $i=0$ in questo caso $X\to Y\in F$ e quindi banalmente sarà anche in $F^{+}$

Induzione: Per l’ipotesi induttiva, ogni dipendenza funzionale ottenuta a partire da $F$ applicando armstrong un numero di volte minore o uguale a $i-1$ è in $F^{+}$, per $i$ si presentano 3 casi:

1. $X\to Y$ è stata ottenuta mediante l’assioma della riflessività, in tal caso $Y\subseteq X$. Quindi sia $r$ un’istanza di $R$ e siano $t_1,t_2$ due tuple di $r$ tali che $t_1[X]=t_2[X]$ allora banalmente si ha anche che $t_1[Y]=t_2[Y]$.
2. $X\to Y$ è stata ottenuta applicando l’aumento ad una dipendenza $V\to W\in F^A$ tale che $X=VZ$ e $Y=WZ$ per qualche $Z\subseteq R$. Sia $r$ un’istanza legale di $R$ e siano $t_1$ e $t_2$ due tuple di $r$ tali che $t_1[X]=t_2[X]$ si avrà anche che $t_1[V]=t_2[V]$ e $t_1[Z]=t_2[Z]$. Per ipotesi induttiva $t_1[V]=t_2[V]$ porta a $t_1[W]=t_2[W]$ e insieme portano a $t_1[Z]=t_2[Z]$ e quindi otteniamo che $t_1[Y]=t_2[Y]$.
3. $X\to Y$ è stata ottenuta applicando la transitività a due dipendenze funzionali $X\to Z,Z\to Y\in F^A$. Sia $r$ un’istanza di $R$ e siano $t_1,t_2$ due tuple di $r$ tali che $t_1[X]=t_2[X]$ per ipotesi induttiva si ha che $t_1[X]=t_2[X]\Rightarrow t_1[Z]=t_2[Z]$ e sempre per ipotesi induttiva $t_1[Z]=t_2[Z]\Rightarrow t_1[Y]=t_2[Y]$.

• Dimostriamo che $F^{+}\subseteq F^A$

Supponiamo per assurdo che esista una dipendenza funzionale $X\to Y\in F^{+}$ tale che $X\to Y\notin F^A$. Mostreremo che esiste un’istanza legale di $R$ che non soddisfa $X\to Y$ (contraddice il fatto che $X\to Y\in F^{+}$).

Consideriamo la seguente istanza $r$:

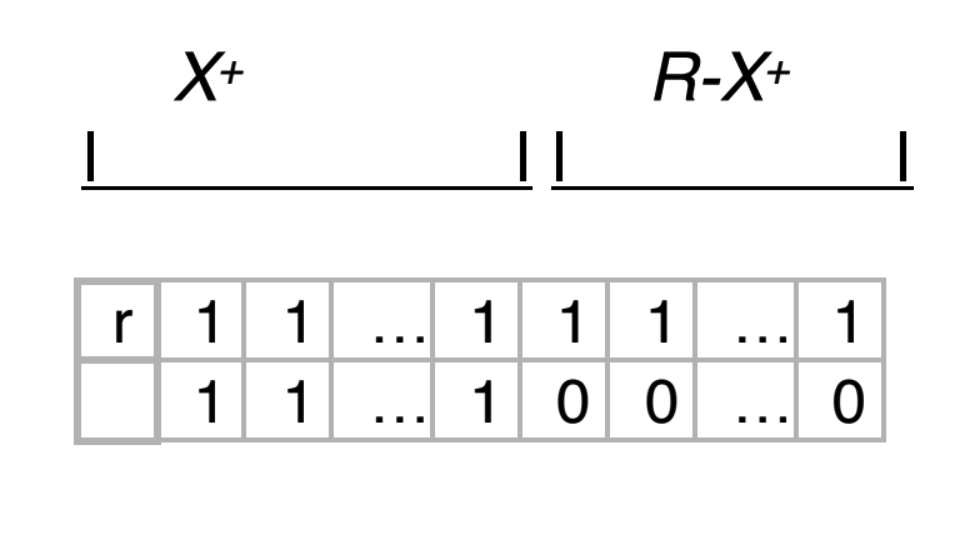
Mostriamo che:

1. $r$ è un’istanza legale di $R$. Sia $V\to W$ una dipendenza funzionale in $F$ e supponiamo per assurdo che non sia soddisfatta da $r$. In tal caso le due tuple devono avere valori uguali su $V$ e diversi per $W$, questo implica che $V\subseteq X^{+}$ e $W\cap (R-X^{+})\ne \varnothing$. Poiché $V\subseteq X^{+}$, per il lemma 1 si ha che $X\to V\in F^A$ e quindi per transitività si ha che $X\to W\in F^A$ e quindi per il lemma 1 $W\subseteq X^{+}$ che contraddice quanto detto prima ovvero che $W\cap (R-X^{+})\ne \varnothing$.
2. In quanto istanza legale, $r$ soddisfa tutte le dipendenze in $F^{+}$, in particolare $X\to Y$. Poiché $X\subseteq X^{+}$ le due tuple di $r$ coincidono sugli attributi $X$ e quindi poiché soddisfa $X\to Y$ devono coincidere anche gli attributi di $Y$, questo implica che $Y\subseteq X^{+}$ e quindi per il lemma 1 che $X\to Y\in F^A$.

---

Calcolare $F^{+}$ richiede tempo esponenziale in $F$, più precisamente esponenziale sul numero di attributi in $R$. Per i nostri scopi è sufficiente determinare se una dipendenza $X\to Y$ appartiene ad $F^{+}$, questo si fa calcolando $X^{+}$ e verificando se $Y\subseteq X^{+}$, il calcolo di $X^{+}$ può essere fatto tramite un algoritmo.

Algoritmo 1: Prende come input uno schema $R$, un insieme $F$ di dipendenze su $R$ e un sottoinsieme $X$ di $R$. Come output fornisce la chiusura di $X$ rispetto ad $F$ all’interno della variabile $Z$.

Teorema 4: L’algoritmo 1 calcola correttamente la chiusura di un insieme di attributi $X$ rispetto ad un insieme $F$ di dipendenze funzionali.

Dimostrazione: Indichiamo con $Z^0$ il valore iniziale di $Z$ ($Z^0=X$) e con $Z^i$ ed $S^i$, $i\ge 1$ i valori di $Z$ ed $S$ dopo l’i-esima esecuzione del ciclo, si vede ad occhio che $Z^i\subseteq Z^{i+1}$, proveremo che esiste $i$ tale che $A\in Z^i$ se e solo se $A\in X^{+}$.

• Parte SE, mostriamo per induzione su $i$ che $Z^i\subseteq X^{+}$ per ogni $i$.

Base Induzione: se $i=0$ dato che $Z^0=X$ e $X\subseteq X^{+}$ si ha che $Z^0\subseteq X^{+}$.

Induzione: $i>0$, per ipotesi abbiamo che $Z^{i-1}\subseteq X^{+}$. Sia $A$ un attributo in $Z^i-Z^{i-1}$, significa che lo abbiamo aggiunto all’ultima iterazione e quindi deve esistere una dipendenza $Y\to V\in F$ tale che $Y\subseteq Z^{i-1}$ e $A\in V$. Dato che $Y\subseteq Z^{i-1}$ otteniamo per ipotesi induttiva che $Y\subseteq X^{+}$ e per il lemma 1 possiamo dire che $X\to Y\in F^A$, inoltre dato che $Y\to V\in F$ possiamo dire per transitività che $X\to V\in F^A$ e quindi per il lemma 1 otteniamo $V\subseteq X^{+}$, quindi per ogni $A\in Z^i-Z^{i-1}$ si ha $A\in X^{+}$, e quindi per l’ipotesi induttiva $Z^i\subseteq X^{+}$.

• Parte SOLO SE: Sia $A$ un attributo in $X^{+}$ e sia $j$ tale che $S^j=Z^j$ ($Z^j$ è il valore di $Z$ quando l’algoritmo termina). Mostreremo che $A\in Z^j$. Poiché $A\in X^{+}$ si ha $X\to A\in F^{+}$ per il teorema 3, pertanto $X\to A$ deve essere soddisfatta da ogni istanza legale di $R$. Consideriamo le seguente istanza $r$:

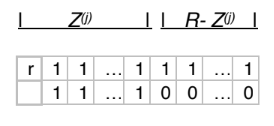
Mostriamo che è legale, se per assurdo esistesse in $F$ una dipendenza funzionale $V\to W$ non soddisfatta da $r$, si dovrebbe avere $V\subseteq Z^j$ e $W\cap (R-Z^j)\ne \varnothing$ ma in tal caso si avrebbe $S^j\ne Z^j$ (contraddizione, significa che non siamo ancora arrivati all’ultima iterazione, ma prima o poi aggiungeremo $W$). Poiché $r$ è un’istanza legale di $R$ deve soddisfare $X\to A$ che si trova in $F^A$ e per il teorema 3 in $F^{+}$, ma allora poiché $X=Z^0\subseteq Z^j$, $A$ deve essere in $Z^j$.

Definizione 7 Sia $R$ uno schema di relazione. Una decomposizione di $R$ è una famiglia $\rho =\{R_1,R_2,\dots ,R_k\}$ di sottoinsiemi di $R$ che ricopre $R$ ovvero ${\bigcup }_{i=1}^k{R}_i=R$.

Definizione 8: Siano $F$ e $G$ due insiemi di dipendenze funzionali. $F$ e $G$ sono equivalenti $F\equiv G$ se $F^{+}=G^{+}$.

Verificare l’equivalenza richiederebbe tempo esponenziale dato che dovremmo calcolare $F^{+}$, usiamo il seguente lemma.

Lemma 2 Siano $F$ e $G$ due insiemi di dipendenze funzionali, se $F\subseteq G^{+}$ allora $F^{+}\subseteq G^{+}$

Dimostrazione Sia $f\in F^{+}-F$, poiché per il teorema 3 $f$ è derivabile fa $F$ mediante gli assiomi di Armstrong e ogni dipendenza funzionale in $F$ è derivabile da $G$ mediante gli assiomi di armstrong, $f$ è derivabile da $G$ mediante gli assiomi di Armstrong.

Essenzialmente dato che $F\subseteq G^{+}$ significa che dentro alla chiusura di $G$ ho anche $F$ ma gli assiomi continuo ad applicarli finché posso e quindi all’interno di $G^{+}$ troverò anche $F^{+}$

Definizione 9 Sia $R$ uno schema di relazione, $F$ un insieme di dipendenze funzionali su $R$ e $\rho =\{R_1,R_2,\dots ,R_k\}$ una decomposizione di $R$ diciamo che $\rho$ preserva $F$ se $F\equiv {\bigcup }_{i=1}^k{\pi }_{Ri}(F)$ dove ${\pi }_{Ri}(F)=\{X\to Y|X\to Y\in F^{+}\wedge XY\subseteq R_i\}$

Verificare che una decomposizione preservi $F$ quindi richiede la verifica dell’equivalenza dei due insiemi $F$ e $G={\bigcup }_{i=1}^k{\pi }_{Ri}(F)$. Per definizione $G\subseteq F^{+}$ quindi ci basta verificare che $F\subseteq G^{+}$.

Algoritmo 2

L’algoritmo richiede che venga calcolato $X_G^{+}$ ma noi non conosciamo $G$, usiamo il prossimo algoritmo:

Algoritmo 3

Teorema 5: Sia $R$ uno schema di relazione, $F$ un insieme di dipendenze funzionali su $R$ e $\rho =\{R_1,R_2,\dots ,R_k\}$ una decomposizione di $R$ e $X$ un sottoinsieme di $R$. L’algoritmo 3 calcola correttamente $X_G^{+}$.

Dimostrazione

Indichiamo con $Z^0$ il valore iniziale di $Z(=X)$ e con $Z^i$ il valore dopo la i-esima iterazione dell’assegnazione $Z=Z\cup S$, quindi si nota che $Z^i\subseteq Z^{i+1}$ per ogni $i$. Inoltre indichiamo con $Z^f$ il valore di $Z$ quando l’algoritmo termina.

Mostriamo che $X_G^{+}\subseteq Z^f\iff Z^f\subseteq X_G^{+}$

Dimostriamo per induzione soltanto $Z^f\subseteq X_G^{+}$.

Base Induzione: Abbiamo che $Z^0\subseteq X_G^{+}$ infatti $Z^0=X$ e quindi è vero per riflessività.

Ipotesi Induttiva: Fino a $i-1$ quello che abbiamo in $Z^{i-1}\subseteq X_G^{+}$ (questo significa che $X\to Z^{i-1}\in G^{+}$).

Passo Induttivo: Banalmente abbiam che $Z^{i-1}\subseteq Z^i$ e per ipotesi induttiva quelli in $Z^{i-1}$ sono già nella chiusura di $G$. Controlliamo quindi le $A\in Z^i-Z^{i-1}$ ovvero aggiunte al passo $i$.

Questo significa che esiste un $j$ tale che $A\in (Z^{i-1}\cap R_j{)}_F^{+}\cap R_j$, questo significa dire che $A$ appartiene ad entrambi i pezzi dell’intersezione, quindi:

$$A\in (Z^{i-1}\cap R_j{)}_F^{+}\wedge A\in R_j$$

La parte a destra per ora non ci interessa, la parte a sinistra implica che:

$$Z^{i-1}\cap R_j\to A\in F^{+}$$

Adesso siccome sappiamo che $A\in R_j$, poi sappiamo che $(Z^{i-1}\cap R_j)\subseteq R_j$ e inoltre la dipendenza si trova in $F^{+}$, ricordando la definizione di $G$ possiamo dire che la dipendenza si trova anche in $G$, infatti:

$$(Z^{i-1}\cap R_j\to A)\in {\pi }_{Rj}(F)\Rightarrow (Z^{i-1}\cap R_j\to A)\in G$$

Adesso, abbiamo:

• Per ipotesi $X\to Z^{i-1}\in G^{+}$
• $Z^{i-1}\to Z^{i-1}\cap R_j$ per riflessività
• Applicando la transitività otteniamo $X\to Z^{i-1}\cap R_j$
• Applicando di nuovo la transitività con $Z^{i-1}\cap R_j\to A$ otteniamo che $X\to A\in G^{+}$

---

Definizione 10: Sia $R$ uno schema di relazione. Una decomposizione $\rho$ di $R$ ha un join senza perdita se per ogni istanza legale $r$ di $R$ si ha $r={\pi }_{R_1}(r)\bowtie \cdots \bowtie {\pi }_{Rk}(r)$.

Teorema 6: Sia $R$ uno schema di relazione e $\rho$ una decomposizione di $R$. Per ogni istanza legale di $R$, indicato con $m_p(r)={\pi }_{R_1}(r)\bowtie \cdots \bowtie {\pi }_{Rk}(r)$ si ha:

• $r\subseteq m_p(r)$ questa è la parte importante, ovvero finché abbiamo $\subseteq$ significa che abbiamo perdita nel join, ovvero il join contiene più tuple dell’istanza, nel momento in cui sono $=$ allora abbiamo join senza perdita. (per ogni istanza legale)
• ${\pi }_{Ri}(m_p(r))={\pi }_{Ri}(r)$
• $m_p(m_p(r))=m_p(r)$

Possiamo capire se una decomposizione ha un join senza perdita tramite il seguente algoritmo:

Algoritmo 4 (Quello con cui costruiamo la tabella): Teorema 7: Sia $R$ uno schema di relazione, $F$ un insieme di dipendenze funzionali su $R$ e $\rho$ una decomposizione di $R$, l’algoritmo 4 funziona.

Dimostrazione: Dobbiamo dimostrare che ha un join senza perdita se e solo se quando l’algoritmo termina la tabella ha una tupla con tutte a.

• Dimostriamo soltanto che se la decomposizione ha un join senza perdita allora la tabella deve avere una riga con tutte a.

Supponiamo per assurdo che $\rho$ abbia un join senza perdita e che con l’algoritmo terminato la tabella $r$ non abbia una tupla con tutte a.

La tabella possiamo vederla come un’istanza legale di $R$ dato che l’algoritmo termina quando non ci sono più violazioni delle dipendenze in $F$.

Poiché nessun simbolo a che compare nella tabella iniziale viene modificato dall’algoritmo, per ogni $i=1,\dots ,k$ abbiamo che ${\pi }_{Ri}(r)$ contiene una tupla con tutte a, quindi questo significa che $m_{\rho }(r)$ contiene una tupla con tutte a dato che prima o poi quelle tuple iniziali si incontreranno nel join. Questo significa che $m_{\rho }(r)\ne r$ almeno per questa istanza infatti abbiamo detto che la tabella non ha una riga con tutte a come ipotesi ma abbiamo trovato un’istanza legale che invece le ha.

Essenzialmente non sappiamo come funziona l’algoritmo perché serve la seconda parte, però, in $m_{\rho }(r)$ ci sarà sempre una riga con tutte $a$ dato che è il join fra i sottoschemi, infatti accade sempre che $r\subseteq m_{\rho }(r)$. Noi però stiamo supponendo che $m_{\rho }(r)=r$ dato che abbiamo join senza perdita e che, per assurdo, in $r$ non ci sia una riga con tutte $a$ ma questo appunto implicherebbe che $r\ne m_{\rho }(r)$. Quindi non stiamo dicendo il “come” funziona l’algoritmo ma soltanto che nel caso di un join senza perdita questo viene rilevato. (Ci ho messo un po’ per capirlo spero di ricapirlo leggendo)

---

Esiste sempre una decomposizione che:

• È in 3NF
• Preserva $F$
• ha un join senza perdita

Possiamo calcolarla in tempo polinomiale tramite un algoritmo ma ci serve il concetto di copertura minimale di un insieme di dipendenze

Definizione 11 Sia $F$ un insieme di dipendenze funzionali, una copertura minimale di $F$ è un insieme $G$ di dipendenze funzionali equivalente ad $F$ e tale che:

• Ogni dipendenza in $G$ ha la parte a destra singleton
• Per nessuna dipendenza $X\to A\in G$ esiste $X^{\prime }\subseteq X$ tale che $G\equiv G-\{X\to A\}\cup \{X^{\prime }\to A\}$ (gli attributi a sinistra non devono essere ridondanti)
• Per nessuna dipendenza $X\to A\in G$ deve accadere $G\equiv G-\{X\to A\}$ (ogni dipendenza non è ridondante).

La copertura non è unica.

Possiamo calcolare una copertura in tempo polinomiale con il seguente algoritmo

Algoritmo 5: Prende in input $R$, $F$ e permette di calcolare una decomposizione che:

• Preserva $F$
• Ogni sottoschema è 3NF

Teorema 8: L’algoritmo funziona

Dimostrazione

• $\rho$ preserva $F$

Se preserva la copertura minimale allora preserva anche l’insieme di partenza dato che sono equivalenti.

Sia $G={\bigcup }_{i=1}^k={\pi }_{Ri}(F)$. Per ogni dipendenza funzionale $X\to A\in F$ otteniamo un sottoschema $XA\in \rho$ (l’algoritmo lo ha creato), quindi queste dipendenze saranno sicuramente in $G$ quindi $F\subseteq G\Rightarrow F^{+}\subseteq G^{+}$.

Invece $G\subseteq F^{+}$ per definizione, quindi $\rho$ preserva $F$.

• Ogni schema è in 3NF

Abbiamo i 3 casi dell’algoritmo da dimostrare.

1. Se $S\in \rho$ allora ogni attributo in $S$ fa parte della chiave di quel sottoschema e quindi $S$ è in 3NF, non ci serve controllare sottoschemi dato che stiamo usando una copertura minimale.

2. Se $R\in \rho$ allora esiste una dipendenza funzionale che coinvolge tutti gli attributi in $R$. Siccome $F$ è una copertura minimale tale dipendenza avrà la forma $R-A\to A$ e sempre perché è una copertura minimale non può esistere una dipendenza $X\to A$ con $X\subseteq R-A$, quindi $R-A$ è chiave del sottoschema $R$. Adesso se prendiamo una qualunque dipendenza $Y\to B\in F$, se $B=A$ allora siccome $F$ è minimale otteniamo che $Y=R-A$ dato che é chiave e quindi $Y$ superchiave non viola la 3NF. Se invece $B\ne A$ allora $B\in R-A$ e quindi $B$ è primo e non viola la 3NF.

3. Se invece $XA\in \rho$ siccome $F$ è minimale non ci possono essere dipendenze $X^{\prime }\to A$ tali che $X^{\prime }\subseteq X$ e quindi $X$ è chiave in $XA$. Prendendo quindi una qualsiasi dipendenza $Y\to B$ tale che $YB\subseteq XA$ abbiamo che se $B=A$ allora $Y=X$ e quindi è superchiave e non viola la 3NF se invece $B\ne A$ allora necessariamente $B\in X$ e quindi è primo e non viola la 3NF.

Se vogliamo ottenere un join senza perdita ci basta aggiungere un sottoschema che contiene una chiave, non facciamo la dimostrazione.

---

Definizione 12: Uno schema è in forma normale Boyce-Codd se per ogni dipendenza funzionale $X\to A\in F^{+}$ tale che $A\notin X$ si ha che $X$ è una superchiave.

Se uno schema è in 3NF Boyce Codd allora è anche in 3NF ma non è vero il contrario.

Non esiste sempre una decomposizione che:

• Tutti schemi in Boyce Codd
• preserva F
• Join senza perdita

Invece esiste sempre:

• Tutti schemi in Boyce Codd
• Join Senza perdita. Ed esiste anche un algoritmo che genera tale decomposizione.