SLIDE DI INTRODUZIONE

Prima per immagazzinare i dati si utilizzavano sistemi informativi dove ogni applicazione aveva il suo file privato, quali erano li svantaggi?

Ridondanza: Se due applicazioni usavano gli stessi dati questi venivano salvati due volte.
Inconsistenza: Se abbiamo due copie, l’aggiornamento di un dato poteva riguardare soltanto una di queste.
Dipendenza dei Dati: Ogni applicazione organizzava i dati in modo diverso, in base all’utilizzo che ne faceva.

Adesso si utilizzano le Basi di Dati (Database) ovvero un insieme di file mutuamente connessi, questi sono organizzati in strutture dati che ne facilitano la creazione e l’accesso, inoltre ottimizzano la gestione delle risorse fisiche.

Si utilizzano i Sistemi di Gestione di Basi di Dati (DBMS) per la gestione di grandi masse di dati residenti su memorie secondarie.

Quando un’informazione viene registrata in formato elettronico ci sono due possibilità:

Dati Strutturati: I dati sono rappresentanti da stringhe di simboli e da numeri.
Dati non strutturati: Rappresentati in linguaggio naturale.

La struttura di un dato dipende dal suo utilizzo e può essere modificate nel tempo, ad esempio se dobbiamo salvare i dati relativi ad una persona ci servirà: nome, cognome, codice fiscale ecc…

L’obiettivo è quello di facilitare l’elaborazione dei dati sulla base delle loro relazioni, infatti possiamo accedere singolarmente agli elementi della struttura tramite “interrogazioni” per recuperare informazioni o effettuare calcoli.

In una base di dati ogni componente è interessata ad una porzione del Sistema Informativo, queste porzioni possono sovrapporsi ma la base di dati ci permette di ridurre le ridondanze e conseguenti inconsistenze.

La condivisione non è mai completa, vanno regolamentati gli accessi e questa comporta il controllo della concorrenza ovvero l’accesso simultaneo allo stesso dato.

Sistema Informativo

Un sistema informativo è un complesso di dati organizzati fisicamente in una memoria secondaria e gestiti in maniera tale da consentirne la creazione, l’aggiornamento e l’interrogazione.

I dati sono organizzati in aggregati di informazioni omogenee che costituiscono le componenti del sistema informativo, ogni operazione ha per oggetto un singolo aggregato mentre un’interrogazione può coinvolgerne più di uno.

Nelle basi di dati:

Aggregati di informazioni omogenee: file
Indici: File che permettono di recuperare velocemente delle informazioni.

L’informazione è rappresentata sotto forma di dati ovvero dei valori che devono essere interpretati e correlati per fornire un’informazione.

Ad esempio “Alessio Marini” e ‘1234567890’ sono una stringa e un numero ovvero due dati, ma se li vediamo come risposta alla domanda “Di chi sono gli appunti e quel è il suo numero di telefono?” allora costituiscono informazione.

Modello dei dati

Sono strutture da utilizzare per organizzare i dati e le loro relazioni, un componente fondamentale sono i costruttori di tipo, ad esempio nel modello relazionale abbiamo il costruttore di relazione che organizza i dati come insieme di record.

Ci sono due tipi di modelli:

Modelli Logici: Sono indipendenti dalle strutture fisiche ma sono disponibili nei DBMS.
Modelli Concettuali: Sono indipendenti dalle modalità di realizzazione e hanno lo scopo di rappresentare le entità del mondo reale e le loro relazione nella prima fase della progettazione.

Modello Relazionale

Nel 1970 IBM introduce il Modello Relazionale, i dati e le relazioni vengono rappresentati come valori e non ci sono riferimenti espliciti come puntatori, garantendo quindi una rappresentazione di alto livello.

Oggetto: record
Campi: Informazioni di interesse

Ad esempio:

Oggetto: “Membro dello Staff”
Campi: Codice, Cognome, Nome, Ruolo, Anno di Assunzione

CODICE COD1 COGNOME Rossi NOME Mario RUOLO Analista ASSUNZIONE 1995

Tabella: Insieme di record di tipo omogeneo, creiamo ad esempio la Tabella STAFF ovvero l’insieme di record di tipo “Membro dello Staff”:

CODICE COD1 COD2 COD3 COGNOME Rossi Bianchi Neri NOME Mario Pietro Paolo RUOLO Analista Analista Amministratore ASSUNZIONE 199519901985

Esempio più completo di DB Relazionale

Studenti:

MATRICOLA 276545485745200768 COGNOME Smith Black Verdi NOME Mary Anna Paolo DATA NASCITA 25/11/1980 23/04/1981 12/02/1981

Corsi:

CODICE 010304 TITOLO Physics Chemistry Chemistry TUTOR Grant Beale Clark

Esami:

STUDENTE 276545276545200768 VOTO C B B CORSO 010401

Abbiamo la tabella Esami che mette collega i corsi e gli studenti.

DB e DBMS

Il Database è la collezione di dati logicamente correlati di interesse per il Sistema Informativo

Il DBMS è un software che interagisce con il DB da una parte e con i programmi applicativi dall’altra

Oggetti nella base di Dati: Memorizzano proprietà di “Oggetti” e relazioni tra oggetti nel dominio di interesse.

Le componenti di un Sistema Informativo Informatizzato sono quindi:

La base di dati BD
Un DBMS
Applicativo software che utilizza il DB
Hardware del computer, ovvero i dispositivi di memorizzazione.
Personale che gestisce il sistema.

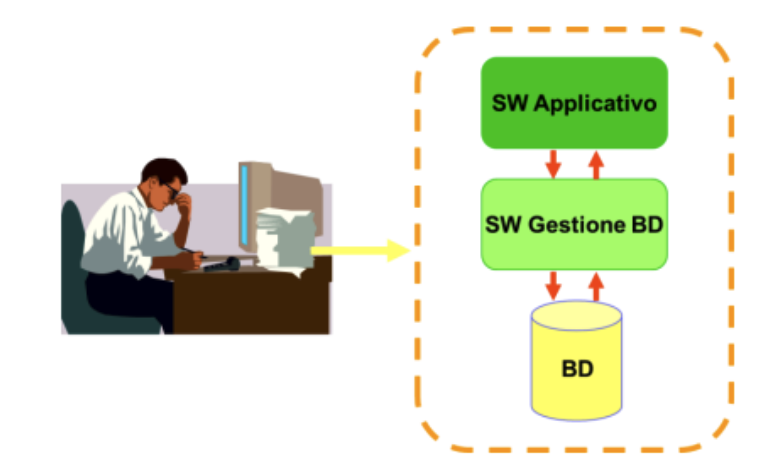
La memorizzazione avviene in maniera astratta, ovvero, i sistemi di basi di dati utilizzano dei formati proprietari per salvare i dati, ma offrono all’utente una vista “normale” dell’oggetto memorizzato, in modo da rendere trasparenti i dettagli di memorizzazione e manipolazione.

Livelli di Astrazione di un DB

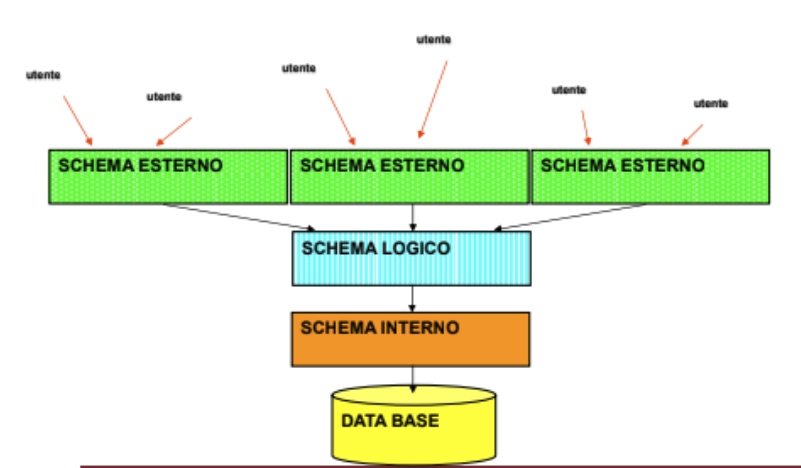
Schema Esterno:Descrizione di una porzione della base di dati in un modello logico attraverso delle viste parziali che possono prevedere organizzazioni dei dati diverse rispetto a quelle utilizzate nello schema logico, queste riflettono esigenze e privilegi dell’utente. Ad uno schema logico si possono associare più schemi esterni. (In poche parole non tutti gli utenti devono accedere a tutti i dati, chi ha più privilegi può vedere più cose)
Schema Logico: Descrizione dell’intera base di dati nel modello logico principale del DBMS, come ad esempio la struttura delle tabelle.
Schema Fisico: Rappresentazione dello schema logico per mezzo di strutture fisiche di memorizzazione, i file.

Esempio

Dato lo schema logico:

Una possibile vista CorsiSedi può essere:

Gli accessi alla base avvengono solamente attraverso lo schema esterno che può coincidere o meno con quello logico.

Indipendenza dei Dati

Indipendenza Fisica: Il livello logico e quello esterno sono indipendenti da quello fisico, questo comporta che una relazione è utilizzata nello stesso modo qualunque sia la sua realizzazione fisica ovvero l’organizzazione dei file sulla memoria. Inoltre la realizzazione fisica può cambiare senza causa problemi nei programmi che utilizzano la base di dati.
Indipendenza Logica: Il livello esterno è indipendente da quello logico, infatti aggiunte o modifiche alle viste non richiedono modifiche al livello logico mentre modifiche che allo schema logico che lasciano inalterato lo schema esterno sono trasparenti.

Schemi e Istanze

In ogni base di dati esistono:

Schema: Non cambia nel tempo e ne descrive la struttura, sono le intestazioni delle tabelle.
Istanza: I valori attuali che possono cambiare, sono gli elementi di ogni tabella.

Linguaggi per le Basi di Dati

Data Definition Language (DDL): Per la definizione degli schemi
Data Manipulation Language (DML): Per l’interrogazione e l’aggiornamento delle istanze della base di dati.
SQL (Structured Query Language): Linguaggio standardizzato per database basati sul modello relazionale. In SQL le due funzionalità sono integrate in un unico linguaggio.

Ricapitolando

Le basi di dati sono:

Multiuso
Integrazione
Indipendenza dei dati
Controllo centralizzato (DBA: Database Administrator).

I vantaggi sono:

Minima ridondanza
Indipendenza dei dati
Integrità
Sicurezza

Integrità

I dati devo soddisfare i vincoli imposti dalla realtà di interesse, ad esempio:

Uno studente vive in una sola città, Dipendenze Funzionale.
La matricola identifica univocamente uno studente, Vincoli di Chiave.
Un voto è un intero positivo compreso tra 18 e 30, Vincoli di Dominio.
Lo straordinario di un impiegato è dato dal prodotto del numero di ore per la paga oraria, lo stipendio non può diminuire, Vincoli Dinamici.

Sicurezza

I dati devono essere protetti da accessi non autorizzati, il DBA deve considerare chi può accedere a quali dati e in quale modalità e decidere il regolamento di accesso e gli effetti di una violazione, inoltre i dati devono essere protetti da malfunzionamenti hardware, software e dall’accesso concorrente alla base di dati.

Ad esempio una transazione deve essere eseguita completamente, committed oppure non deve essere eseguita affatto rolled back.

Per ripristinare un valore corretto si usa il transaction log che contiene i dettagli delle operazioni, si esegue il dump ovvero la copia dei dati.

Concorrenza

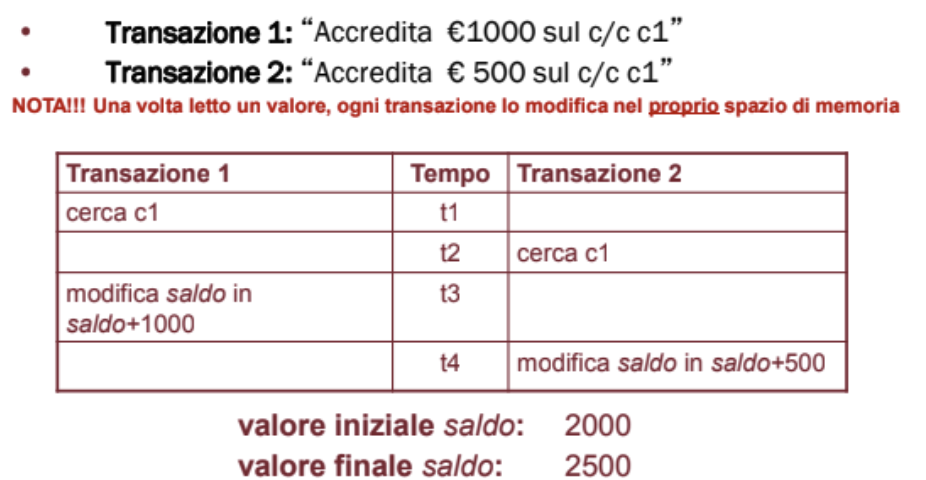
La transazione 1 ha impostato il saldo a 2000 + 1000 mentre la due avendo letto il dato prima della fine della 1 lo ha impostato a 2000 + 500 e terminando per ultima lo ha impostato come valore finale. Per questo è importante gestire la concorrenza.

Il compito di un DBA è quindi:

Definizione e descrizione di:
- Schema Logico
- Schema Fisico
- Viste
Mantenimento:
- Modifiche per nuove esigenze o efficienza
- Routine (analisi, ripristino ecc…)

Modello Relazionale

Si basa sul concetto matematico di relazione, queste sono come delle tabelle e d’ora in poi le chiameremo appunto relazioni.

Relazione matematica.
Relazione secondo il modello relazionale dei dati.
Relazione che rappresenta un’associazione nel modello Entità - Relazioni, rappresenta un collegamento concettuale tra entità diverse.

Definizioni

Dominio: un insieme, anche infinito, di valori. Siano D1, D2,…,Dk domini, il prodotto cartesiano di tali domini è dato da:

{(v 1, v 2, ..., v k) ∣ v 1 \in D 1, v 2 \in D 2, ..., Vk \in D k}

Una relazione matematica è un sottoinsieme del prodotto cartesiano di uno o più domini.
Una relazione che è sottoinsieme del prodotto cartesiano di $k$ domini si dice di grado k. (grado = numero di domini)
Gli elementi di una relazione sono detti tuple, il numero di tuple di una relazione indica la cardinalità di quest’ultima. (cardinalità = numero di coppie ordinate, ovvero tuple).
Ogni tupla di una relazione di grado $k$ ha $k$ componenti ordinate (attributi) ma non c’è ordinamento tra le tuple.
Le tuple di una relazione sono tutte distinte almeno per un valore dai vincoli sugli insiemi. (Almeno un elemento deve cambiare fra ciascuna).

Esempio

Supponiamo che $k = 2$ e i due domini sono $D 1 = {bian co, n ero}$ e $D 2 = {0, 1, 2}$ , il prodotto cartesiano è dato da $D 1 \times D 2 = {(bian co, 0), (bian co, 1), (bian co, 2), (n ero, 0), (n ero, 1), (n ero, 2)}$ .

Come relazioni possiamo prendere:

${(bian co, 0), (n ero, 0), (n ero, 2)}$ : Ha come cardinalità 3 e come grado 2.
${(n ero, 0), (n ero, 2)}$ : Ha come cardinalità 2 e come grado 2.

Spesso si usano come domini comuni ai linguaggi di programmazione come String, Integer, Boolean.

Notazioni

Se $r$ è una relazione di grado $k$

Se $t$ è una tupla di $r$

Se $i$ è un numero intero nell’insieme ${1, ..., k}$

Allora $t [i]$ indica la i-esima componente di $t$

Esempio

Se $r = {(0, a), (0, c), (1, b)}$
$t = (0, a)$
$t [2] = a, t [1] = 0, t [1, 2] = (0, a)$

Relazioni e Tabelle

Per interpretare le tabelle dobbiamo assegnare dei nomi a queste e alle loro colonne:

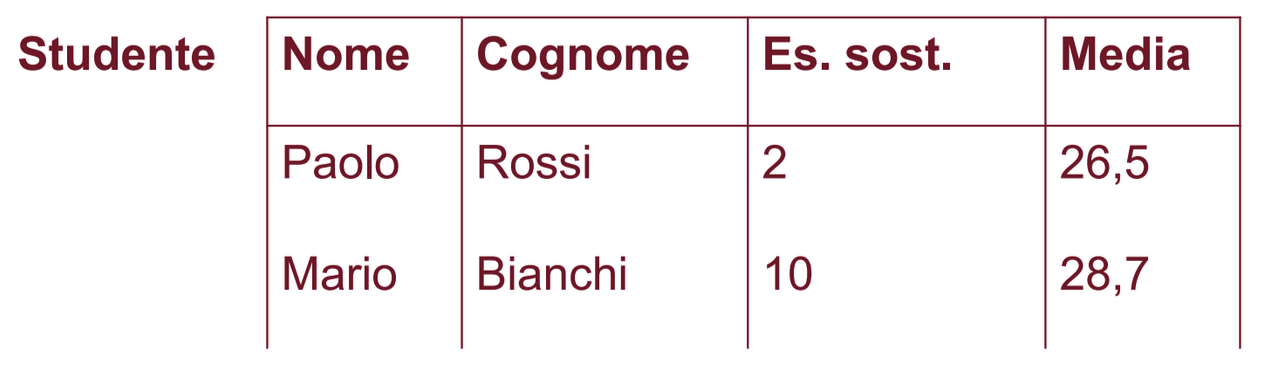
Un attributo è definito da un nome A e dal dominio dell’attributo A che indichiamo con dom(A).
Sia $R$ un insieme di attributi, un’ennupla su $R$ è una funzione definita su $R$ che associa ad ogni attributo $A$ in $R$ un elemento di dom(A).
Se $t$ è un’ennupla su $R$ ed $A$ è un attributo in $R$ , allora con $t (A)$ indicheremo il valore assunto dalla funzione $t$ in corrispondenza dell’attributo A.

Vediamo gli elementi graficamente:

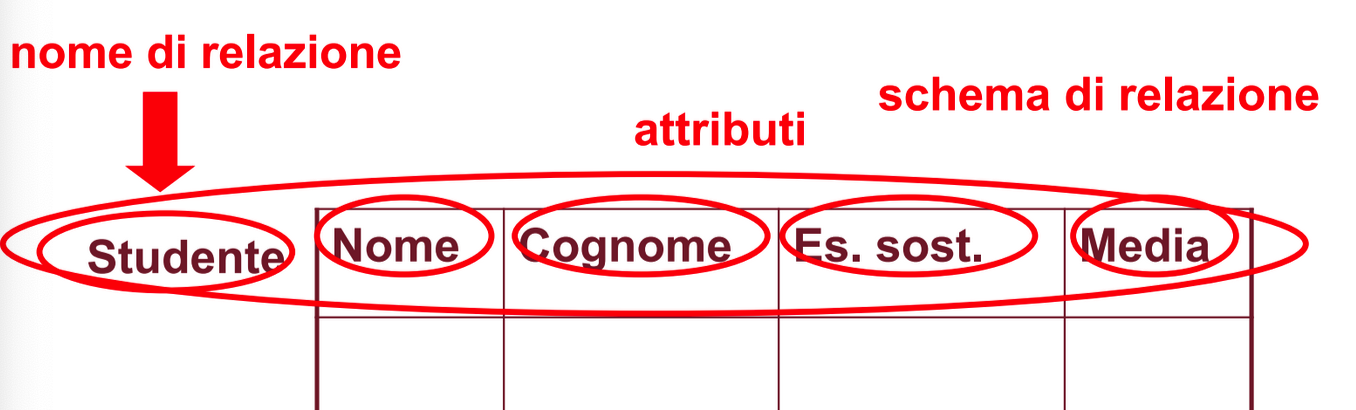
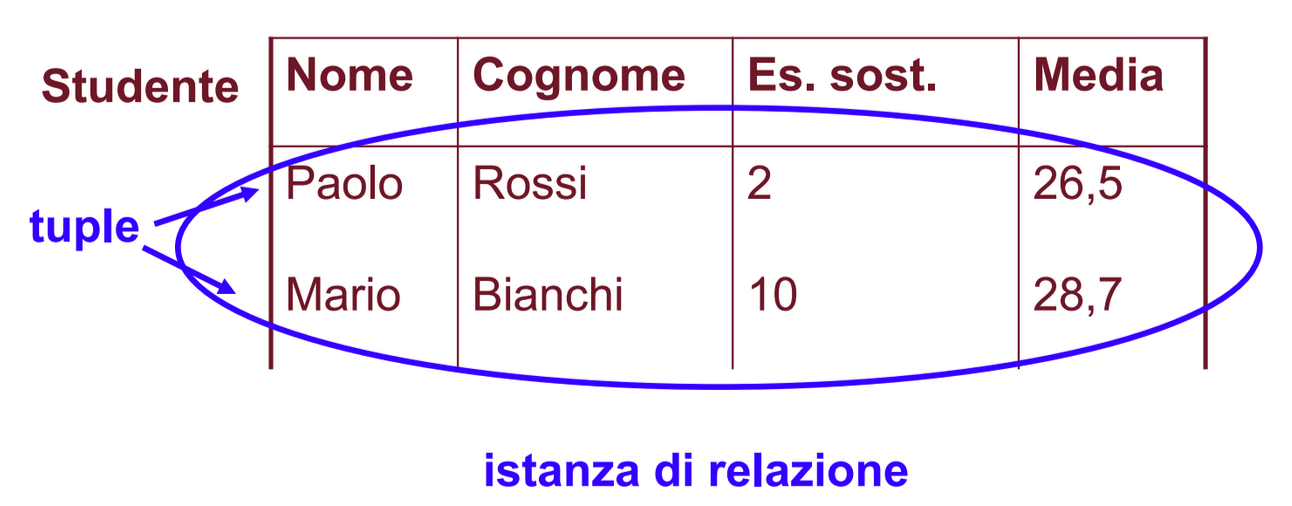
Quindi:

Una relazione possiamo implementarla come una tabella dove ogni riga è una tupla della relazione e ogni colonna è un attributo.
Le colonne corrispondono ai domini e hanno associati dei nomi univoci, detti nomi degli attributi.
L’insieme degli attributi di una relazione è detto schema
Se una relazione è denominata da $R$ e i suoi attributi hanno nomi A1, A2, …, Ak lo schema è indicato da $R (A 1, A 2, ..., A k)$ , questo è lo schema di relazione.
Lo schema spesso è invariante nel tempo e descrive la struttura della relazione.
L’istanza di una relazione è un’insieme di tuple. (i valori presenti nella tabella)
L’istanza contiene i valori attuali e possono anche cambiare molto spesso.
Schema di base di dati: Un insieme di schemi di relazione con nomi differenti (un insieme di tabelle).
Schema di base di dati relazionale: Insieme ${R_{1}, R_{2}, ..., R_{n}}$ di schemi di relazione
Base di dati relazionale con schema ${R_{1}, R_{2}, ..., R_{n}}$ : un insieme ${r_{1}, r_{2}, ..., r_{n}}$ dove $r_{i}$ è un’istanza di relazione con schema $R_{i}$ . Quindi lo schema della base sono l’insieme delle strutture delle tabelle mentre la base di dati sono i valori presenti nelle rispettive tabelle (istanze).

Esempio

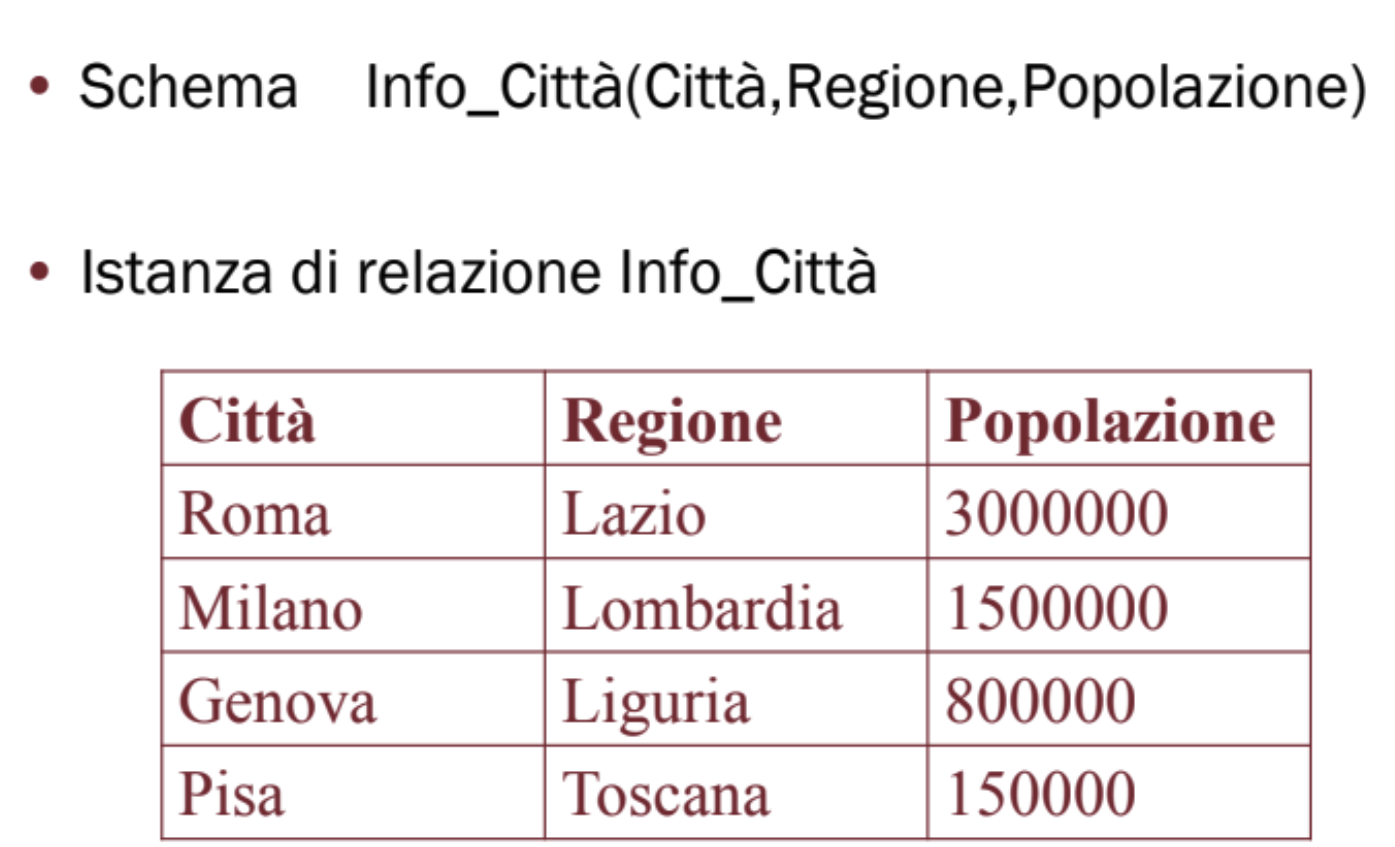
Prima abbiamo utilizzato la notazione $t [i]$ per indicare il valore ad un determinato attributo di una tupla con $i$ intero, adesso si utilizza $t [A i]$ con $A i$ nome dell’attributo, ad esempio se prendiamo seconda tupla dell’esempio sopra $t [R e g i o n e] = L o mba r d ia$ .

Se $Y$ è un sottoinsieme di attributi dello schema $X$ di una relazione allora $t [Y]$ è il sottoinsieme dei valori nella tupla $t$ che corrispondono ad attributi contenuti in $Y$ , detto restizione di $t$ .

Valori

Nel modello relazionale i riferimenti fra dati in relazioni diverse sono rappresentati per mezzo di valori dei domini che compaiono nelle ennuple.

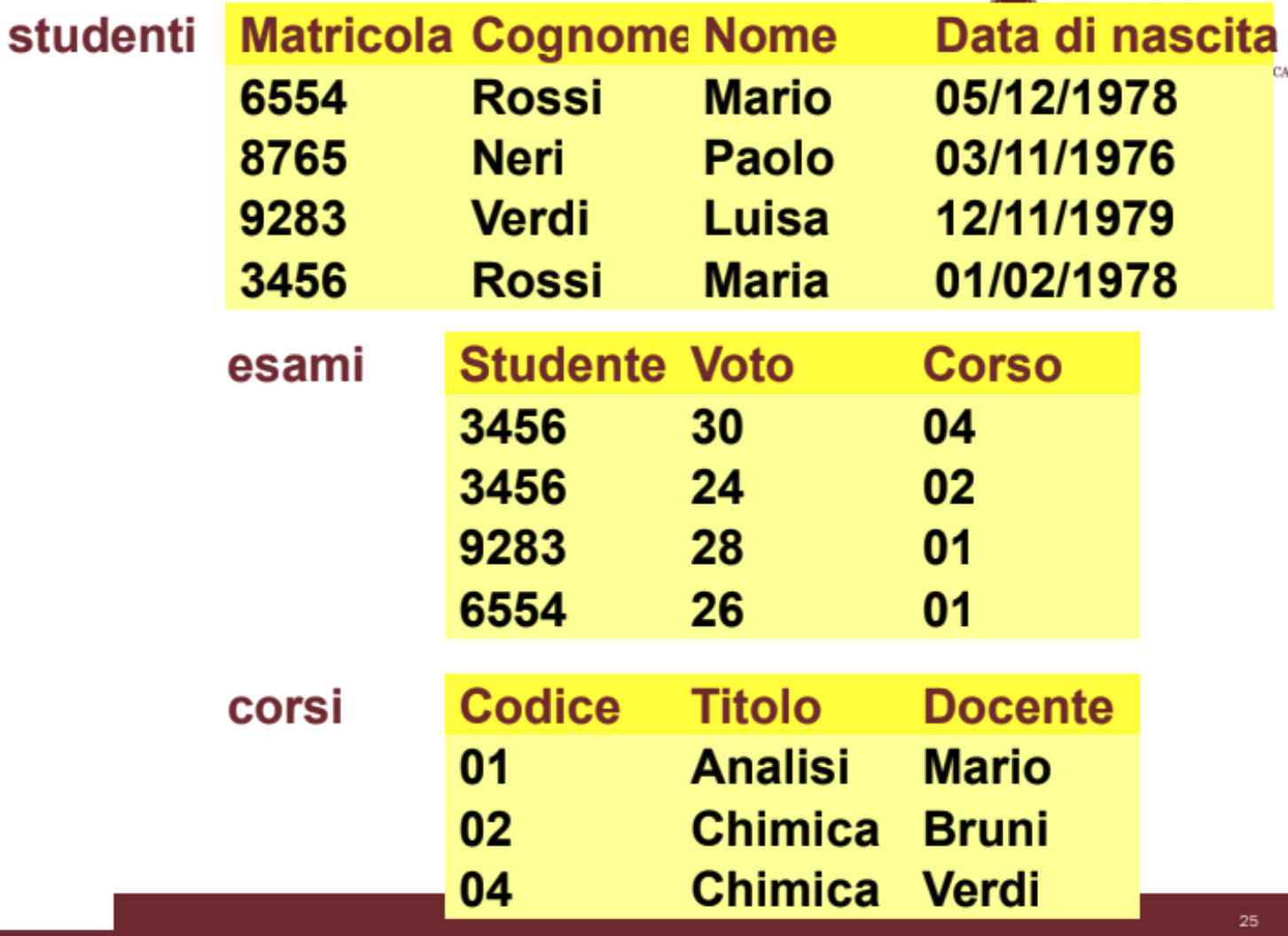
Qui ad esempio la tabella Esami mette in relazione gli Studenti e i Corsi rispettivamente tramite la Matricola e il Codice. Se una tabella contiene un elemento univoco di un’altra questa si chiama slave mentre l’altra master, in questo caso abbiamo quindi due master ovvero Studenti e Corsi mentre lo slave è Esami.

Il master quindi deve esistere prima dello slave altrimenti non è possibile creare il secondo.

All’interno di una tupla è possibile inserire anche dei valori nulli ma non possiamo omettere completamente un campo, le tuple devono seguire tutte lo stesso schema. Se vogliamo “omettere” dei campi possiamo stabilire un valore di default.

Valore Speciale NULL

Il valore null non appartiene a nessun dominio ma può essere assegnato a un dominio qualsiasi (qualsiasi attributo). Se prendiamo confrontiamo due valori null, anche sullo stesso dominio di attributo, questi risulteranno sempre diversi. Non è possibile assegnare NULL ai valori usati come identificativi delle tuple.

Vincoli

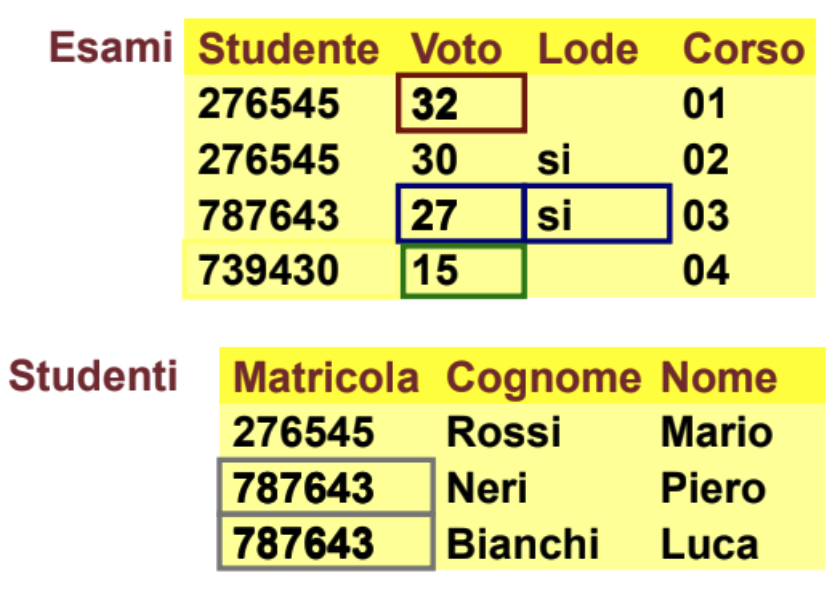
Entrambe questi basi di dati presentano degli errori, nella prima abbiamo una data di assunzione impossibile, un codice impiegato ripetuto ma che è un valore univoco e un codice DIP non esistente.

Nella seconda altri tipi di errori ad esempio 32 un voto che non esiste, una lode con un 27 un valore sotto al 18, mentre sugli studenti una matricola duplicata.

I Vincoli di Integrità sono delle regole che devono essere soddisfatte da ogni istanza della base di dati.

Quindi nel primo caso possiamo stabilire che:

Assunzione deve essere > 1980
Codice impiegato deve essere UNIQUE
Il campo DIP è collegato al campo Dipartimento.Numero. Nella seconda base:
Voto >= 18 AND Voto ⇐ 30
Voto = 30 OR NOT Lode = “si”
Il campo Esami.Studente è collegato a Studenti.Matricola
Matricola deve essere UNIQUE

Possiamo dividerli in due categorie: Vincoli Intra-Relazionali e Vincoli Inter-Relazionali

Vincoli Intra-Relazionali

Sono definiti su valori di singoli attributi oppure tra valori di una stessa tupla o ancora tra tuple della stessa relazione.

Vincoli di chiave Primaria: unica e mai nulla
Vincoli di Dominio: ad esempio Assunzione > 1980
Vincoli di Unicità: li indichiamo con UNIQUE
Vincoli di Tupla: Voto = 30 OR NOT Lode = “si”
Vincoli di esistenza del valore per un certo attributo: NOT NULL
Espressioni sul valore di attributi della stessa tupla: ad esempio orario_partenza < orario_arrivo, con gli orari di un treno.

Vincoli Inter-Relazionali

Sono vincoli definiti tra più relazioni ad esempio:

Impiegato.DIP references dipartimento.numero
Esami.studente references Studenti.Matricola

Chiavi

In un’istanza di relazione dobbiamo identificare univocamente le tuple di una relazione e per fare questo utilizziamo le chiavi, la chiave può essere un attributo o un insieme di attributo.

Un insieme $X$ di attributi di una relazione $R$ è una chiave se soddisfa le seguenti condizioni:

Per ogni istanza di $R$ , non esistono due tuple $t 1$ e $t 2$ che hanno gli stessi valori per tutti gli attributi in $X$ , ovvero che $t 1 [X] = t 2 [X]$ . Quindi i valori in questi attributi devono essere tutti diversi fra le tuple, unici.
Nessun sottoinsieme proprio di X soddisfa la condizione 1. Questo significa che la chiave può essere semplicemente quel sottoinsieme, ovviamente dovremo ricontrollare la seconda condizione anche all’interno di quest’ultimo.

Nel caso in cui un sottoinsieme proprio di $X$ non soddisfi la seconda condizione, $X$ prende il nome di superchiave. Una chiave è anche superchiave dato che è unsieme che contiene se stessa.

Una relazione potrebbe avere più chiavi alternative e si sceglie quella più usata o quella composta da un numero minore di attributi, questa prende il nome di chiave primaria. Questa non ammette valori nulli, deve esserci sempre una chiave dato che le tuple non possono essere uguali e inoltre consentono di mettere in relazione diverse tabelle fra loro.

Vincolo di Integrità Referenziale

Delle informazioni presenti in relazioni diverse possono essere messe in relazione fra loro tramite le foreign key:

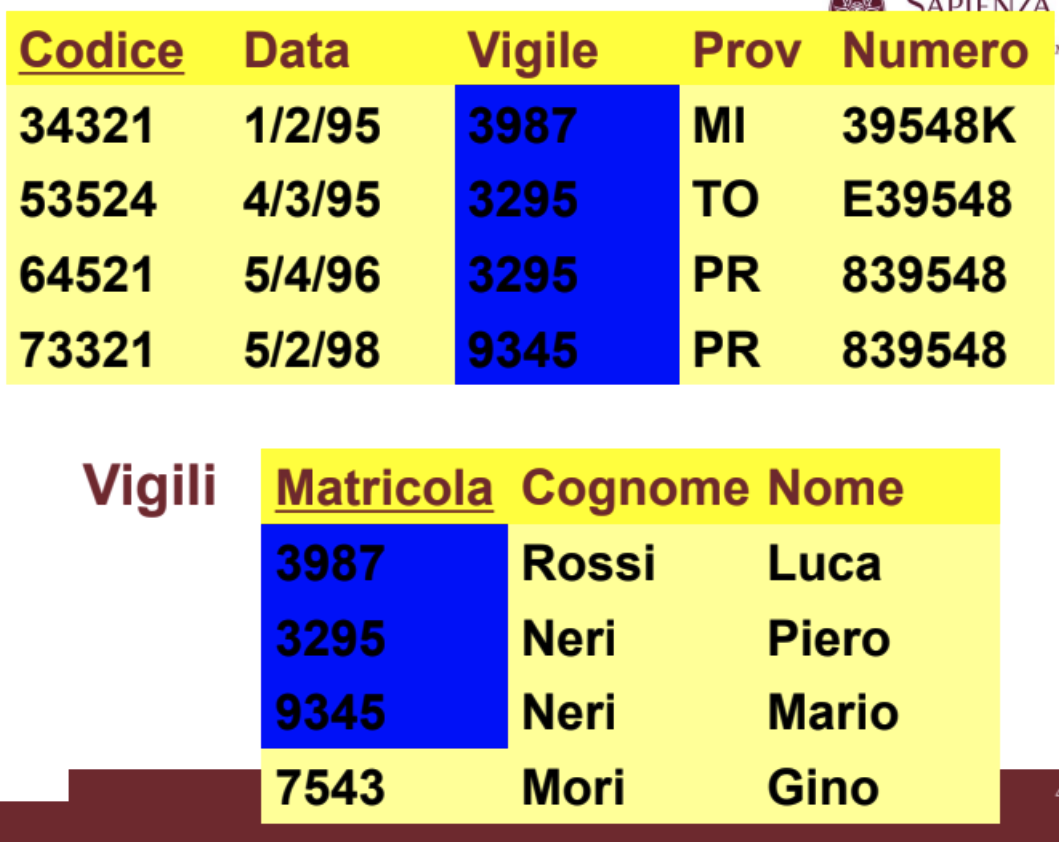
Nella tebella Infrazioni l’attributo Vigile è una foreign key che la mette in relazione con la tabella Vigili.

Come detto prima la chiave può essere composta da più attributi:

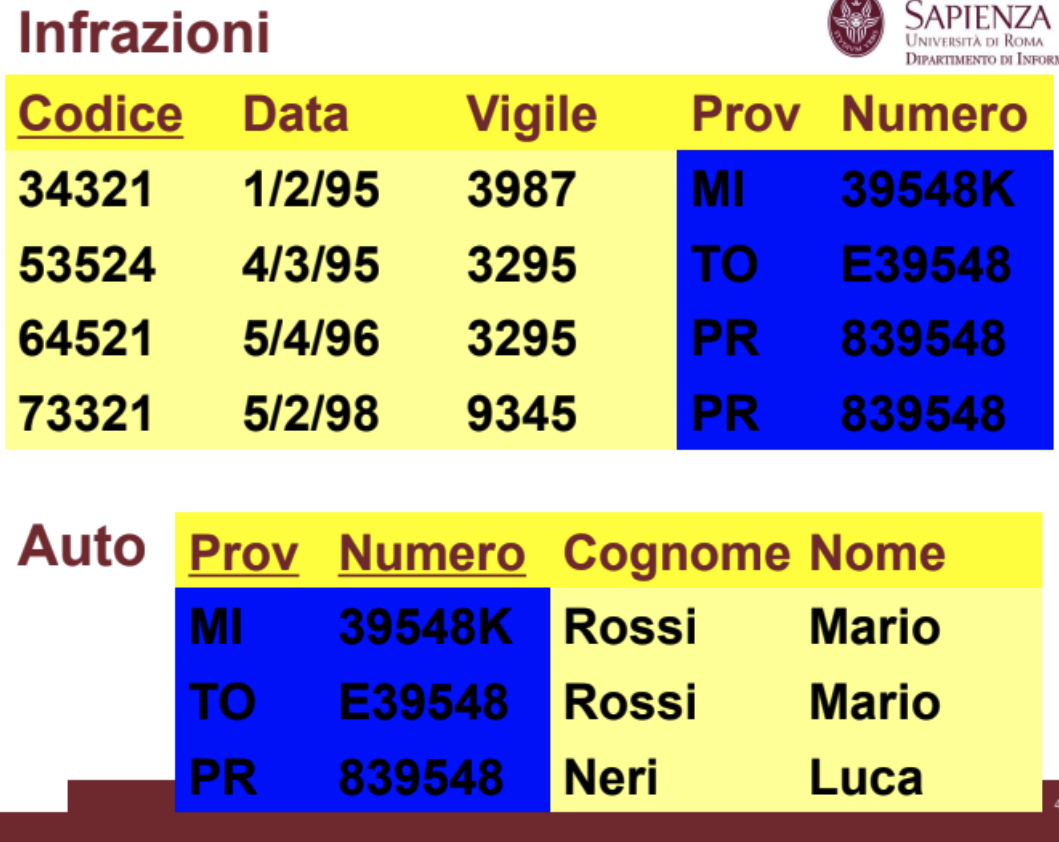
In questo caso la chiave primaria della Relazione Auto è formata da Prov e Numero e quindi in Infrazioni sono presenti entrambe le informazioni come foreign key.

Le Chiavi si stabiliscono in base alle Dipendenze Funzionali.

Dipendenze Funzionali

Una dipendenza funzionale stabilisce un legame semantico tra due insiemi non vuoti di attributi $X, Y$ appartenenti ad uno schema $R$ .

Il vincolo si scrive $X \to Y$ e si legge $X$ determina $Y$ .

Esempio

Il nostro schema è: VOLI(CodiceVolo, Giorno, Pilota, Ora).

Stabiliamo dei vincoli:

Un volo con un certo codice parte sempre alla stessa ora
Esiste un solo volo con un dato pilota, in un dato giorno ad una data ora
C’è un solo pilota di un dato volo in un dato giorno. Otteniamo le seguenti dipendenze funzionali:
CodiceVolo → Ora (Dato che un volo con lo stesso codice parte sempre alla stessa ora)
{Giorno, Pilota, Ora} → CodiceVolo (Dato che c’è un solo volo con un determinato pilota, giorno e ora)
{CodiceVolo, Giorno} → Pilota (Dato che c’è un solo pilota dato un volo in un dato giorno)

Questo significa che come chiave posso usare l’insieme {CodiceVolo, Giorno} dato che CodiceVolo mi determina l’ora e con CodiceVolo e Giorno posso determinare il Pilota.

Non posso usare ad esempio soltanto il CodiceVolo dato che in quel caso saprei soltanto a che ora parte l’aereo ma non saprei chi sarà il pilota e che giorno partirà.

Diremo che una relazione $r$ soddisfa la dipendenza funzionale $X \to Y$ se:

La dipendenza funzionale $X \to Y$ è applicabile a $R$ , ovvero che $X, Y$ sono sottoinsiemi di $R$ .
Le ennuple in $r$ che concordano su $X$ concordano anche su $Y$ , ovvero per ogni coppia di ennuple $t 1$ e $t 2$ in $r$ abbiamo che $t 1 [X] = t 2 [X] \Rightarrow t 1 [Y] = t 2 [Y]$ . Prendendo l’esempio di prima quindi, se due tuple concordano sul CodiceVolo (X) devono concordare anche sull’ora (Y).
Nel caso in cui $X \cup Y = R$ allora ci basta verificare che prese due tuple qualsiasi $t 1 [X] = t 2 [X]$ per stabilire che la dipendenza non è rispettata.

X prende il nome di Determinante e Y di Dipendente, inoltre un’istanza si dice legale quando soddisfa tutte le dipendenze funzionali.

Algebra Relazionale

Linguaggio Formale per interrogare una base di dati relazionale: Consiste in un insieme di operatori che possono essere applicati ad una o due relazioni e forniscono come risultato una nuova istanza di relazione.

Inoltre è un Linguaggio Procedurale: L’interrogazione consiste in un’espressione in cui compaiono operatori dell’algebra e istanze di relazioni della base di dati, in una sequenza che stabilisce l’ordine delle operazioni e i loro operandi.

Proiezione

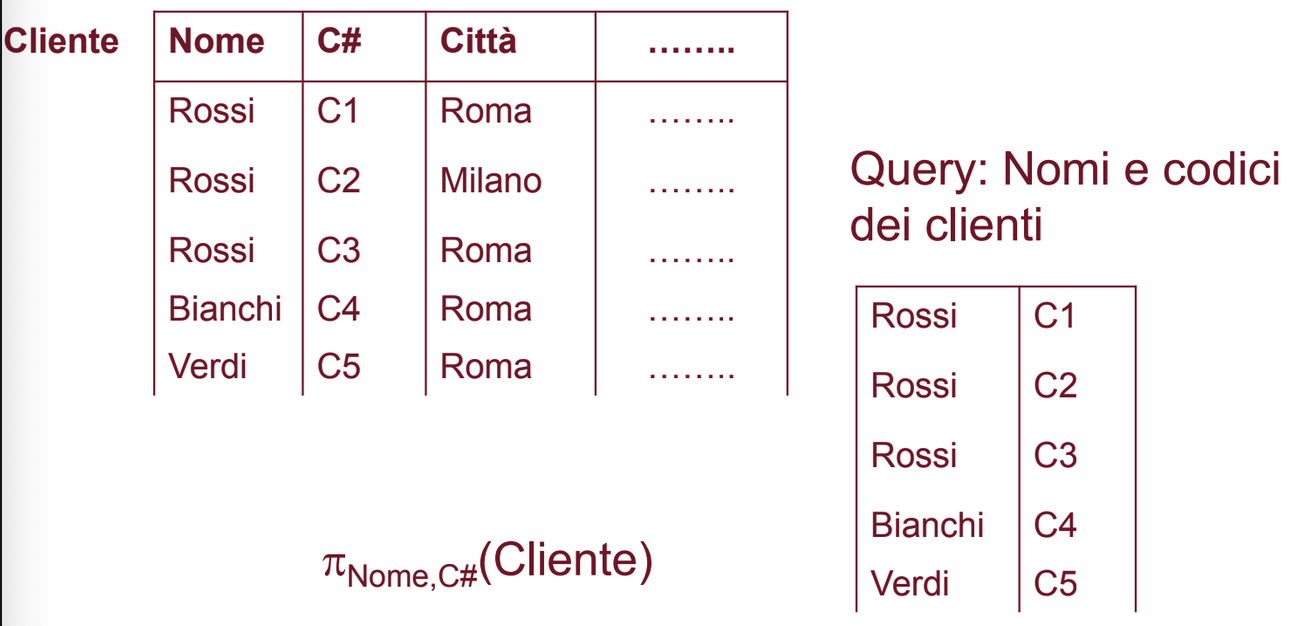
Consiste nell’effettuare un taglio verticale su una relazione, ovvero selezionare soltanto alcuni attributi di essa.

Si denota con il simbolo $π$ ad esempio $π_{A_{1}, A_{2}, \dots A_{k}} (r)$ , in questo modo stiamo selezionando le colonne di $r$ che corrispondono agli attributi $A 1, A 2, \dots A k$ .

Esempio

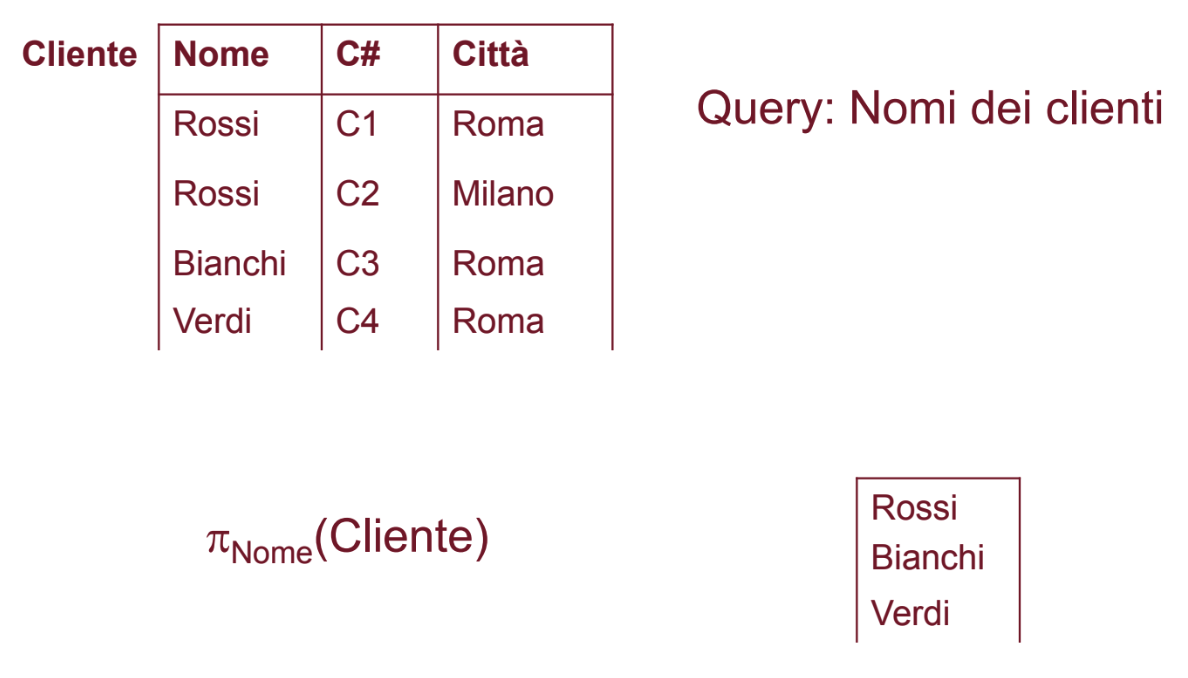
NOTA: Si seguono le regole insiemistiche e quindi nella relazione risultato non ci sono duplicati, notiamo però che abbiamo cancellato delle ennuple significative, ovvero delle ennuple che sono in realtà diverse se consideriamo tutti gli attributi.

Dobbiamo considerare nella proiezione anche un attributo in più, in questo caso la chiave ovvero C#:

Selezione

Consente di effettuare soltanto alcune tuple di una relazione.

Si denota con il simbolo $σ_{C} (r)$ , in questo caso seleziona le tuple della relazione $r$ che soddisfano la condizione $C$ .

La selezione è un’espressione booleana composta in cui i termini semplici sono del tipo:

$A θB$ oppure $A θ^{'} a^{'}$

Dove:

$θ$ è un operatore di confronto, $θ \in {<, =, >, \leq, \geq}$
A e B sono due attributi con lo stesso dominio
a è un elemento di dom(A)

Esempio

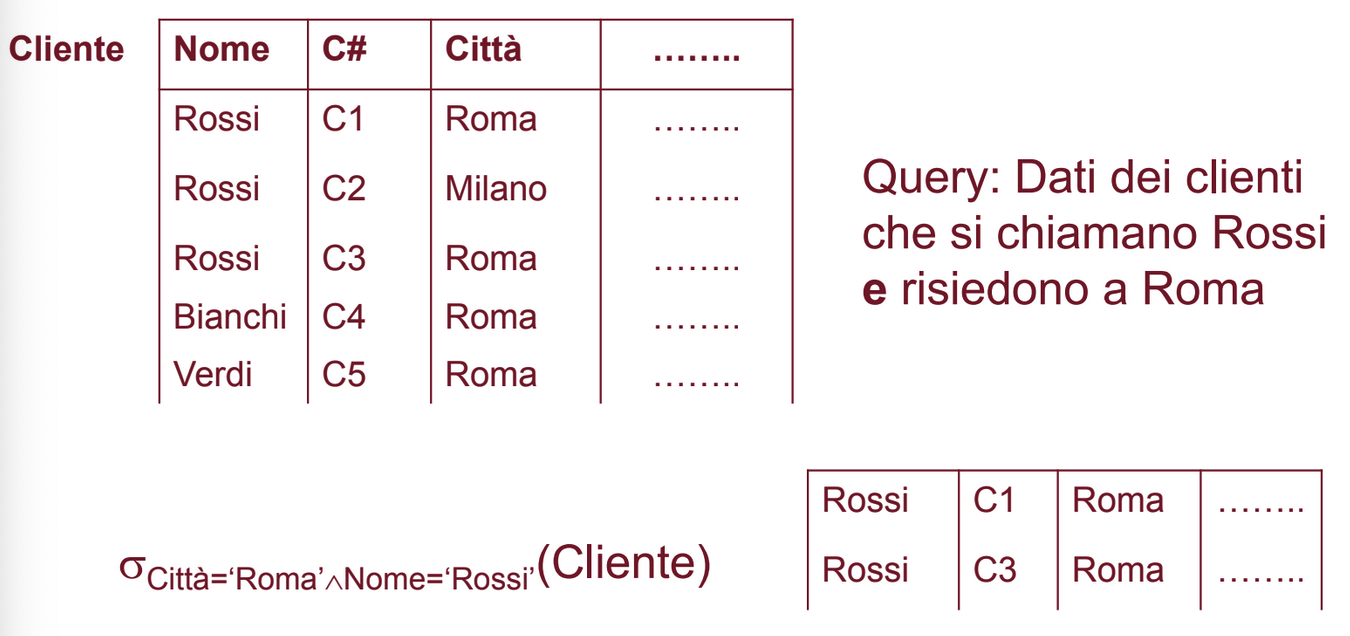
Da notare che al contrario della proiezione, con la selezione non rischiamo di perdere dati significativi.

Unione

Costruisce una relazione contenente tutte le ennuple che appartengono ad almeno uno dei due operandi, si denota con $⋃$

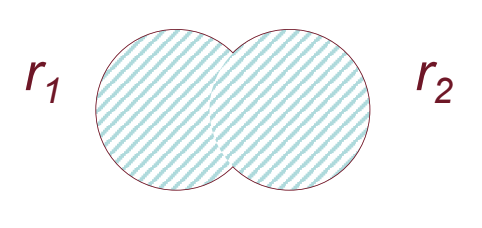
L’unione può essere applicata soltanto ad operandi compatibili ovvero:

Hanno lo stesso numero di attributi
Gli attributi corrispondenti nell’ordine devono avere lo stesso dominio

Gli schemi in questo caso sono detti union compatibili.

Inoltre:

Non è necessario che gli attributi abbiano lo stesso nome ma l’unione ha senso se hanno un significato omogeneo.

Ad esempio Numero di esami ed Età sono definiti sullo stesso dominio ma non avrebbe senso unire due relazioni che hanno questi attributi in colonne corrispondenti.
Uno o entrambi gli operandi possono essere il risultato di operazioni precedenti, ad esempio eliminare gli attributi incompatibili.

Esempio 1

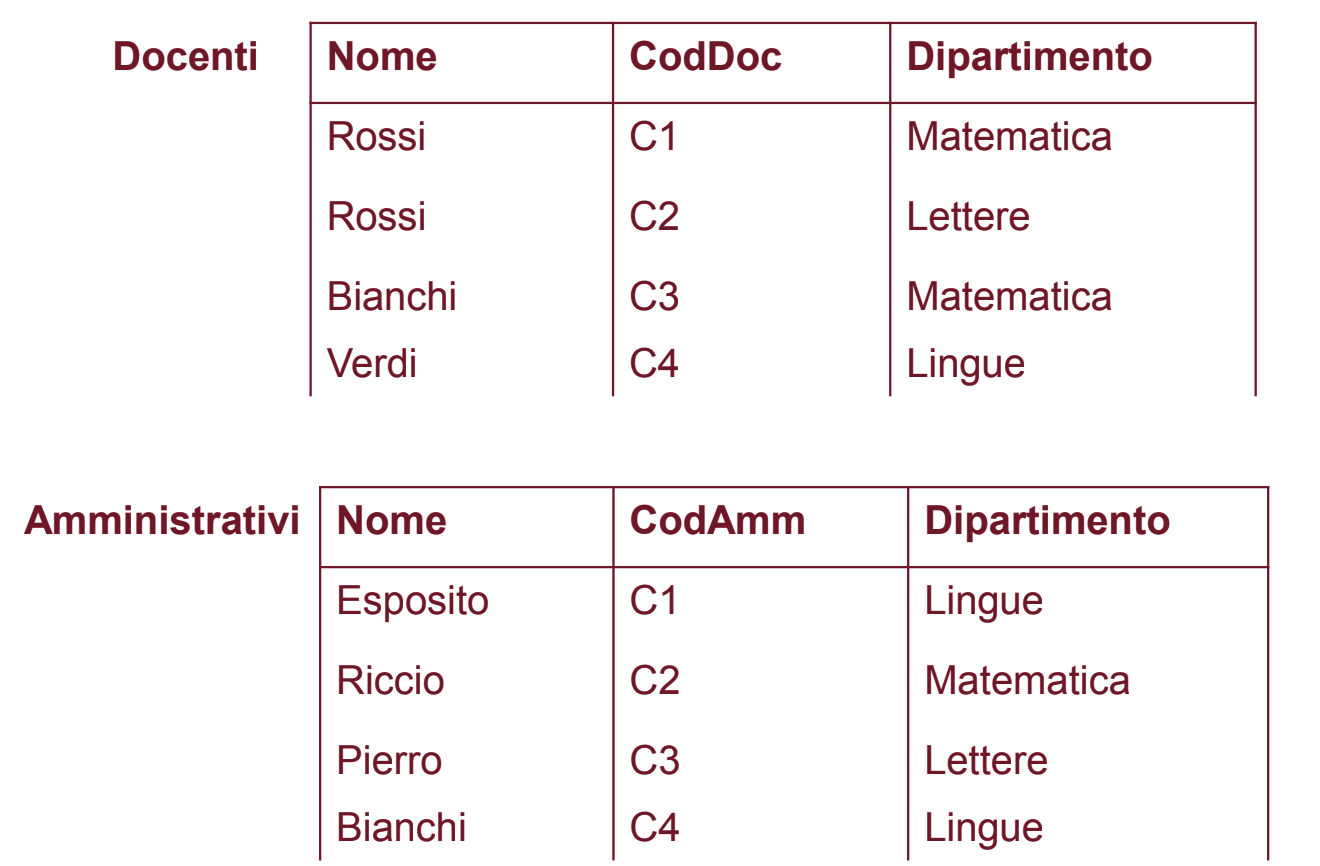
In questo caso l’unione è fattibile, dato che le istanze sono compatibili, otteniamo quindi:

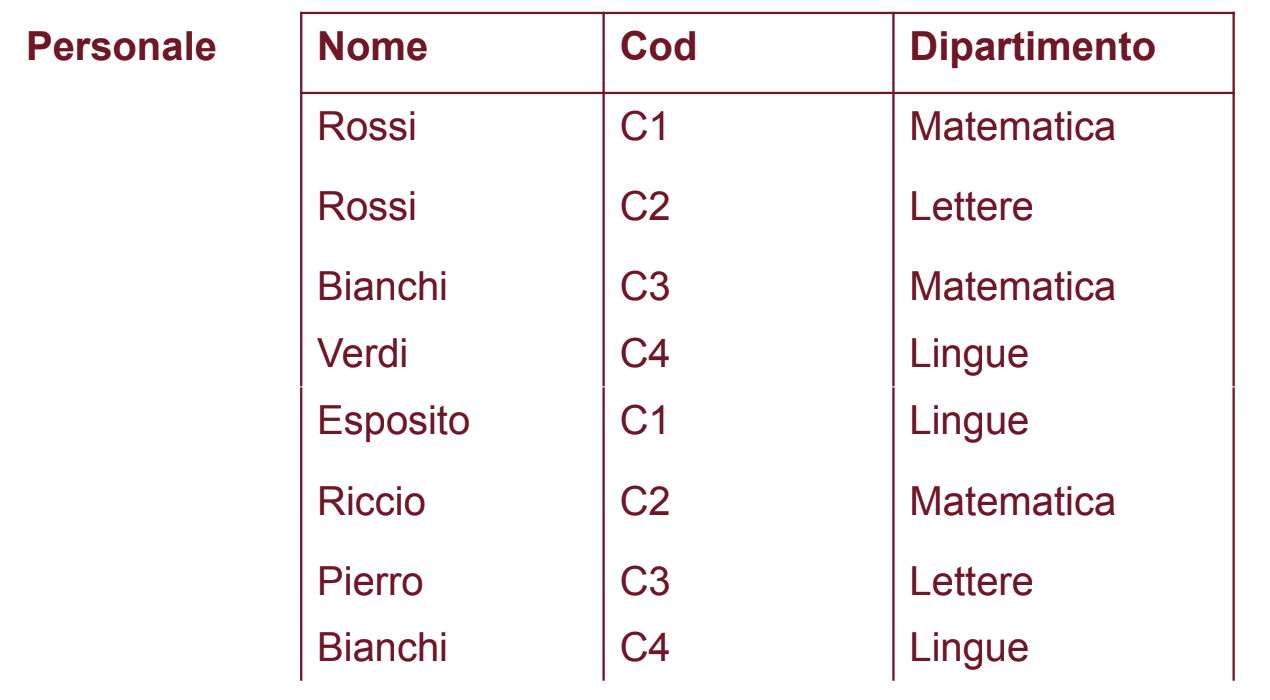
Abbiamo un problema adesso, non riusciamo più a distinguere i Docenti dagli Amministrativi, inoltre dovremmo avere 9 membri del personale ma ne abbiamo solo 8, questo perché una tupla era presente in entrambe le relazioni e quindi è stata riportata una sola volta (Bianchi, C4, Lingue).

Questo è un problema di progettazione, possiamo risolverlo cambiando la notazione per i COD:

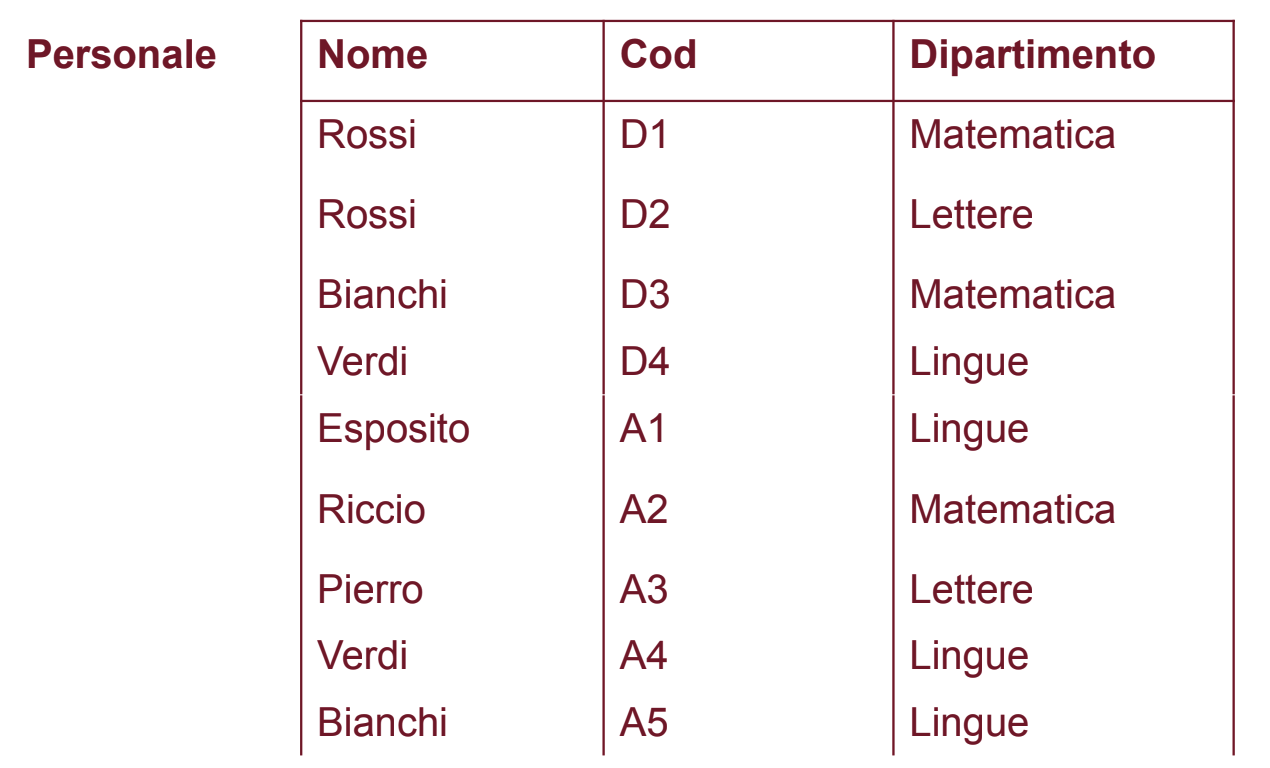
In questo modo vediamo tutto il personale e riusciamo anche a ditinguerli.

Esempio 2

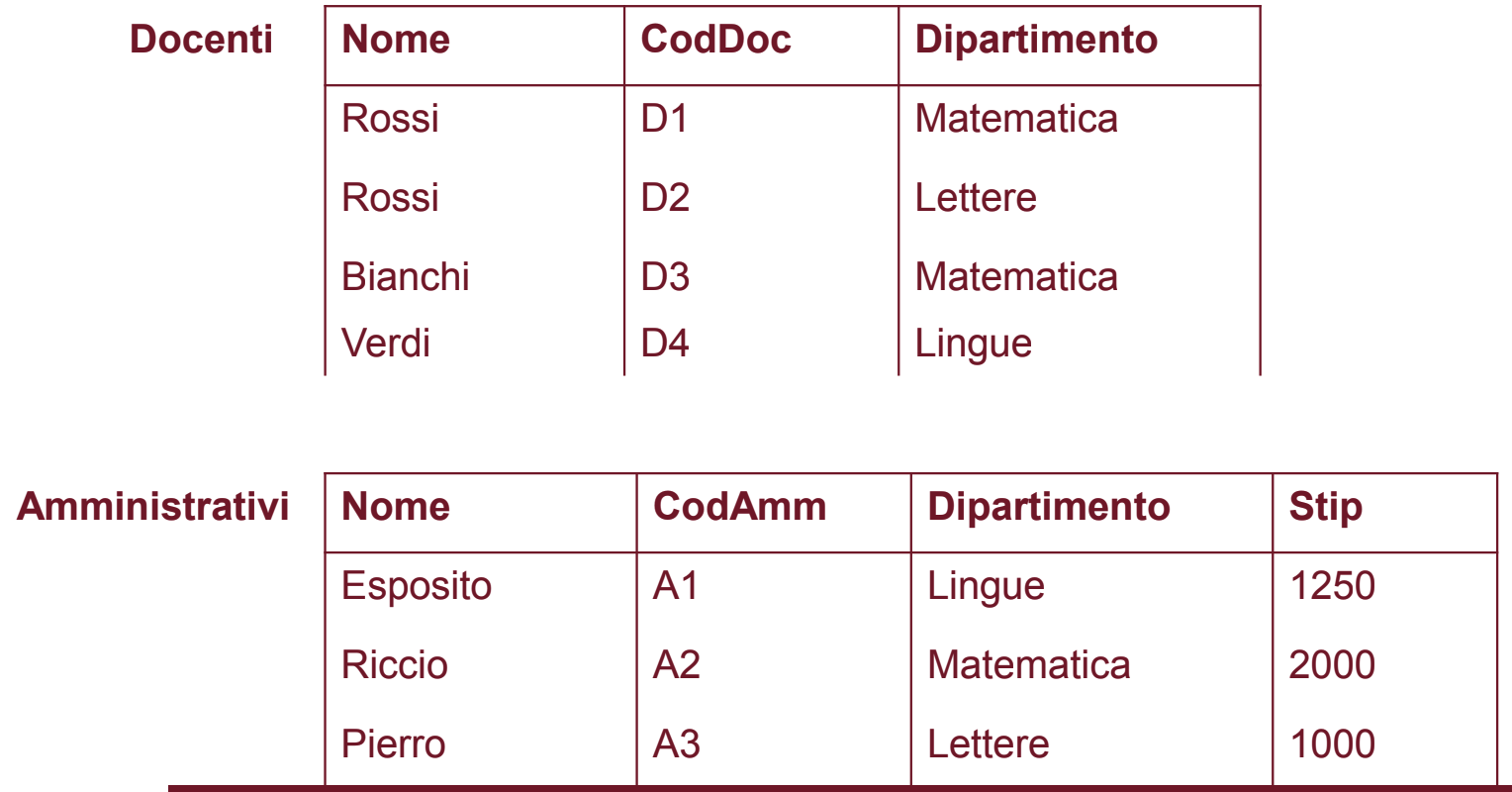
In questo caso non possiamo effettuare l’unione, le due istanze non hanno lo stesso numero di attributi. Come possiamo proseguire?

Possiamo proiettare su un sottoinsieme di attributi comuni (con significato compatibile):

Quindi Amministrativi non ha più l’attributi Stip e quindi le relazioni diventano compatibili.

Esempio 3

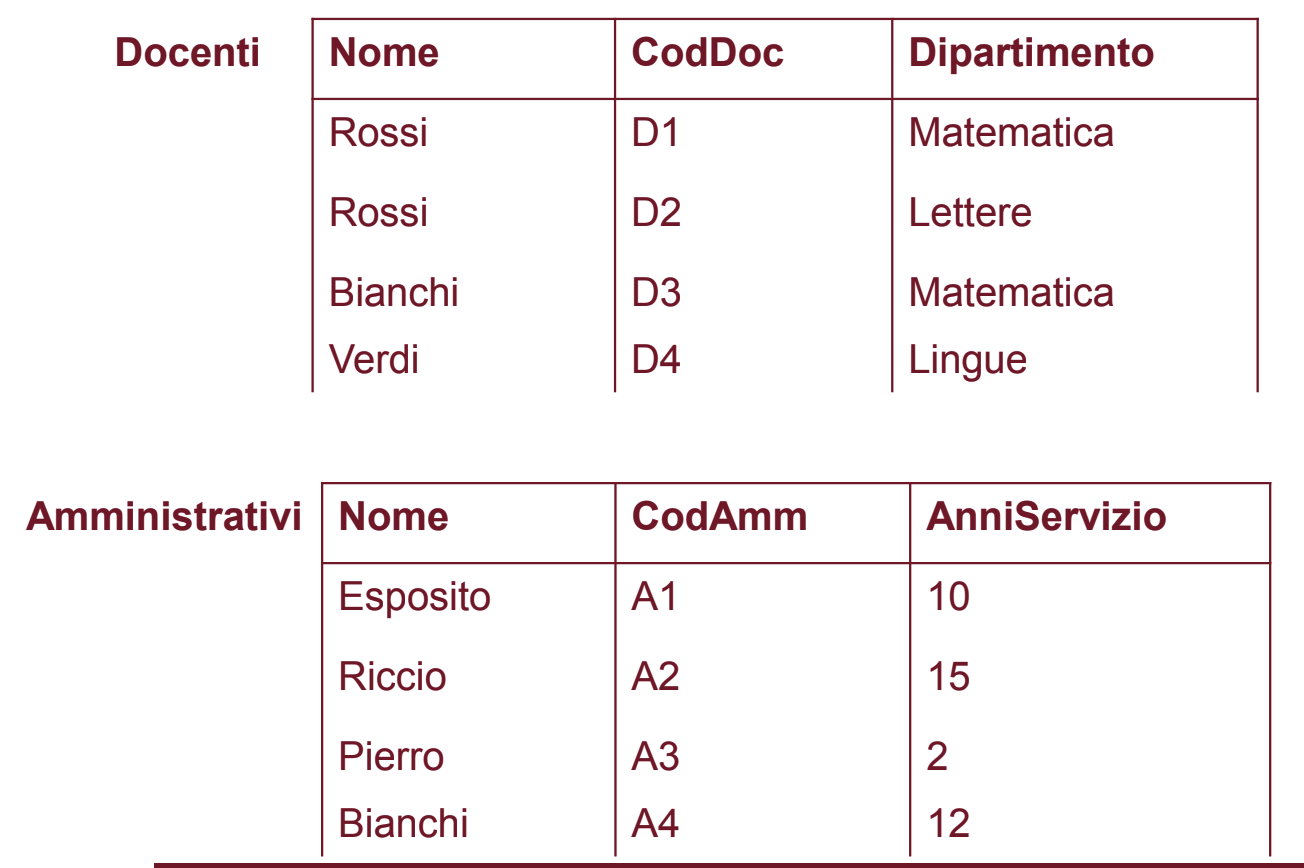
In questo caso non dobbiamo proiettare entrambe le relazioni dato che abbiamo si lo stesso numero di attributi ma Dipartimento e AnniServizio non sono compatibili, dobbiamo quindi rimuoverli entrambi.

Esempio 4

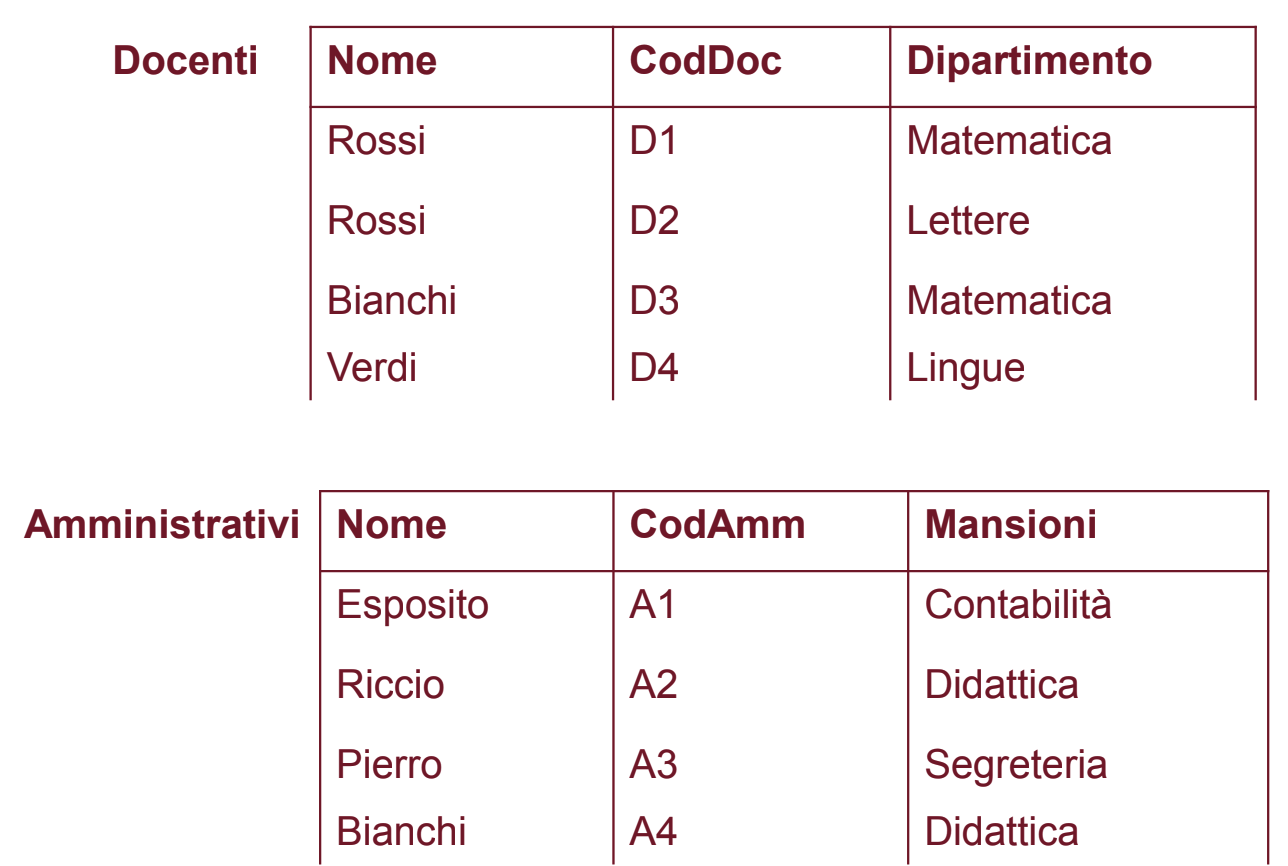
In questo caso Dipartimento e Mansioni hanno lo stesso dominio ma significato diverso, in questo caso possiamo proiettare togliendo i due attributi, come visto prima.

Differenza

Anche la differenza si applica a operandi union compatibili, quindi le condizioni sono uguali a quelle dell’unione.

La differenza consente di costruire una relazione contenente tutte le tuple che appartengono al primo operando e non appartengono al secondo operando.

Si denota con il simbolo $-, r_{1} - r_{2}$ .

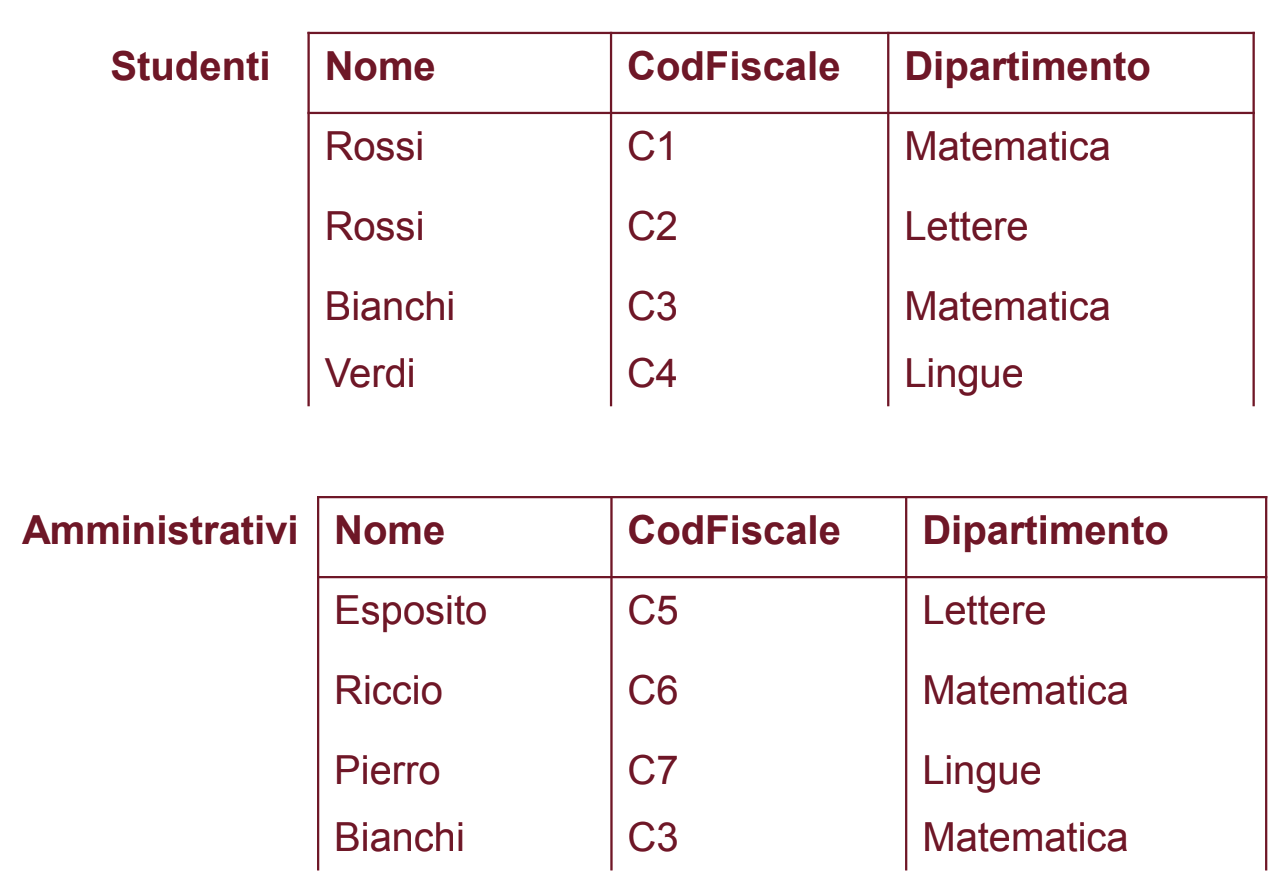
Attenzione, la differenza non è commutativa:

Studenti - Amministrativi: Sono gli studenti che non sono anche amministrativi
Amministrativi - Studenti: Sono gli amministrativi che non sono anche studenti.

Risultati:

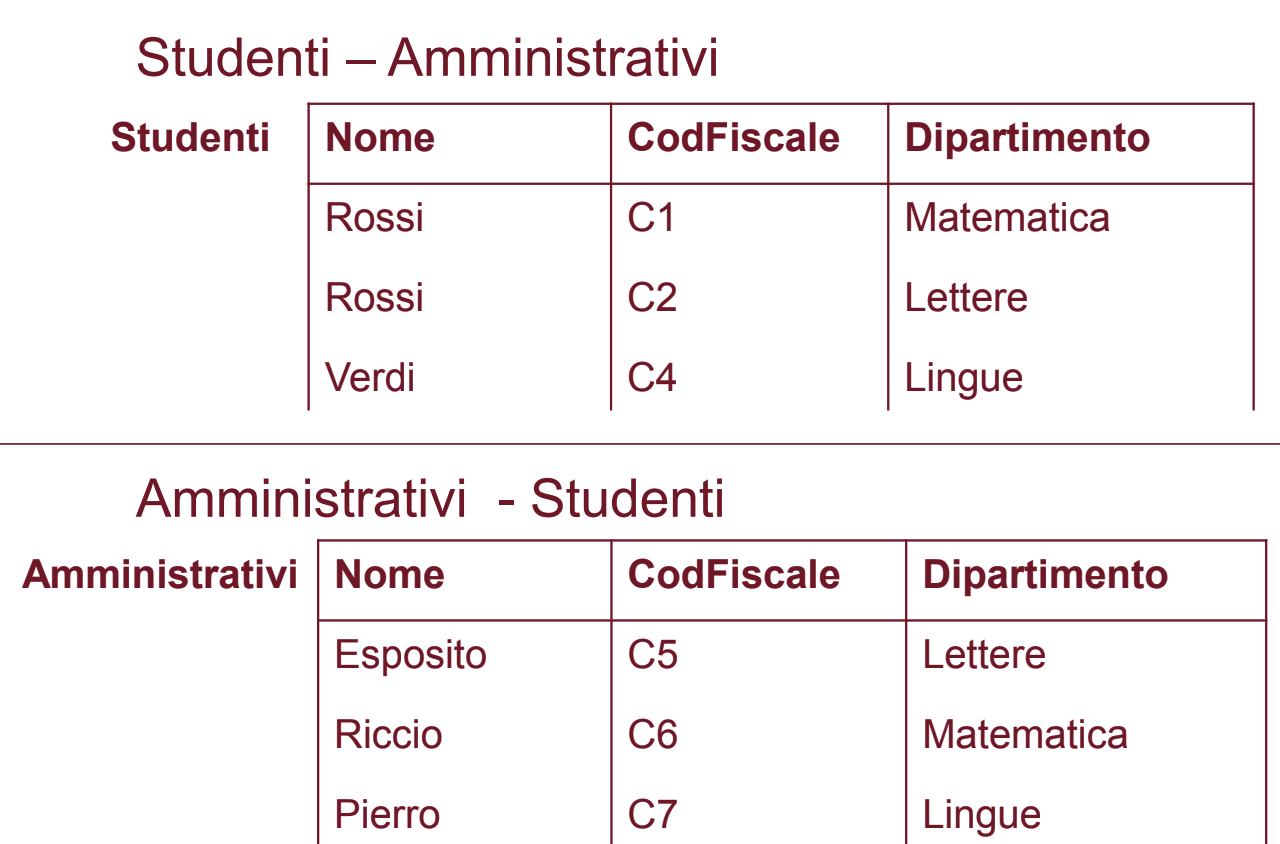
Intersezione

Si applica sempre ad operandi union-compatibili, consente di costruire una relazione contenente tutte le tuple che appartengono ad entrambi gli operandi.

Si denota con $⋂, r_{1} \cap r_{2} = (r_{1} - (r_{1} - r_{2}))$

Esempio

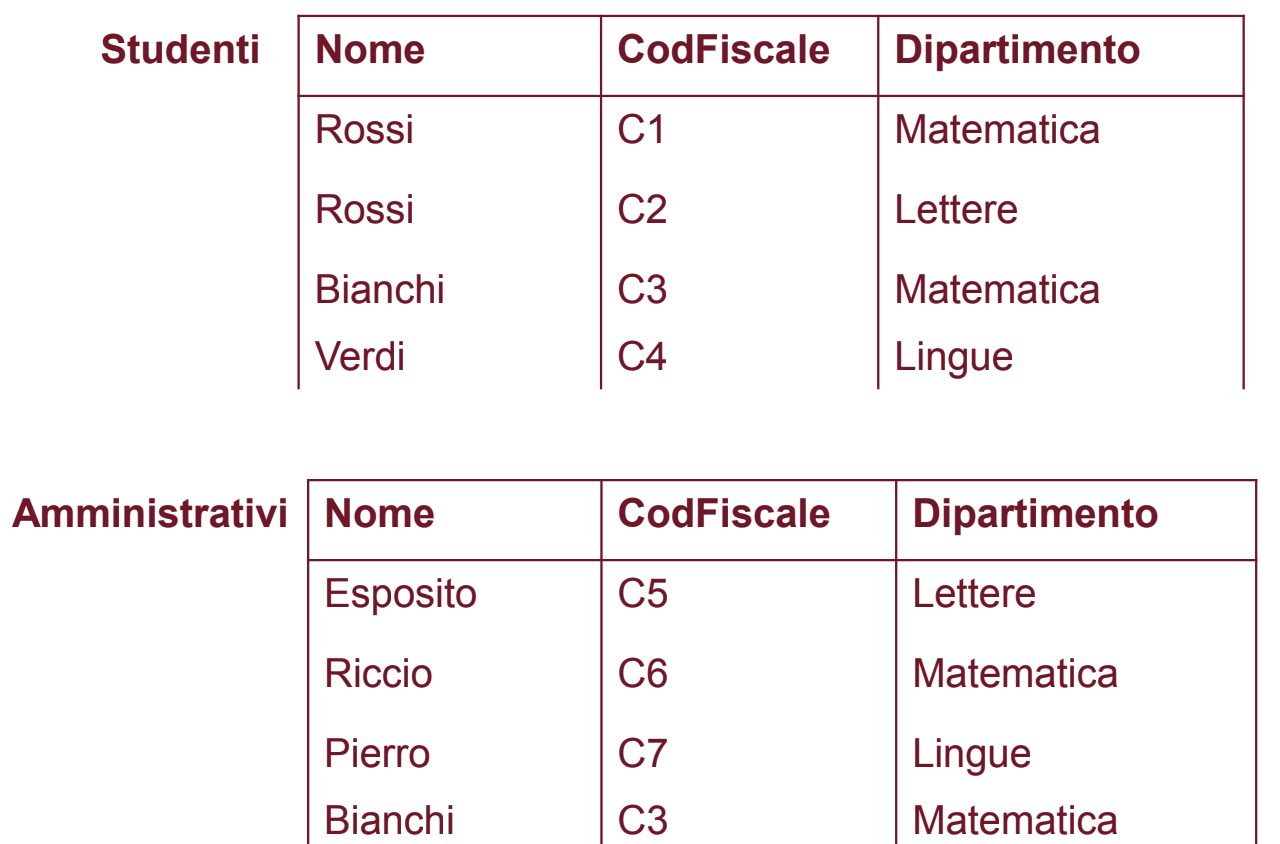
L’operazione intersezione è commutativa.

Come tutte le operazioni, se non rispetto la union-compatibili posso effettuare delle proiezioni.

Algebra Relazionale II

Per garantire un’ottima qualità di una relazione occorre rappresentare in relazioni diverse più concetti. Infatti capita spesso che le informazioni che interessano un’interrogazione sono distribuite in più relazioni dato che coinvolgono più oggetti associati fra loro.

Dobbiamo individuare le relazioni in cui si trovano le informazioni che ci interessano e combinare queste informazioni in modo opportuno.

Prodotto Cartesiano

Consente di costruire una relazione contenente tutte le ennuple che si ottengono concatenando ogni ennupla del primo operando con ogni ennupla del secondo.

Si denota con il simbolo $\times, r_{1} \times r_{2}$ e si utilizza quando le informazioni che occorrono per rispondere ad una query si trovano i relazioni diverse.

In questa operazione non dobbiamo rispettare la union-compatibile e per questo non tutti i risultati che otteniamo hanno un senso.

Esempio

Query: Dati dei clienti e degli ordini ( $Cl i e n t e \times O r d in e$ ).

Per poter distinguere gli attributi con lo stesso nome nello schema risultante possiamo usare l’operazione di ridenominazione per utilizzare una copia della relazione Ordine in cui l’attributo C# diventa CC#. Altrimenti avremmo anche potuto scrivere Ordine.C#.

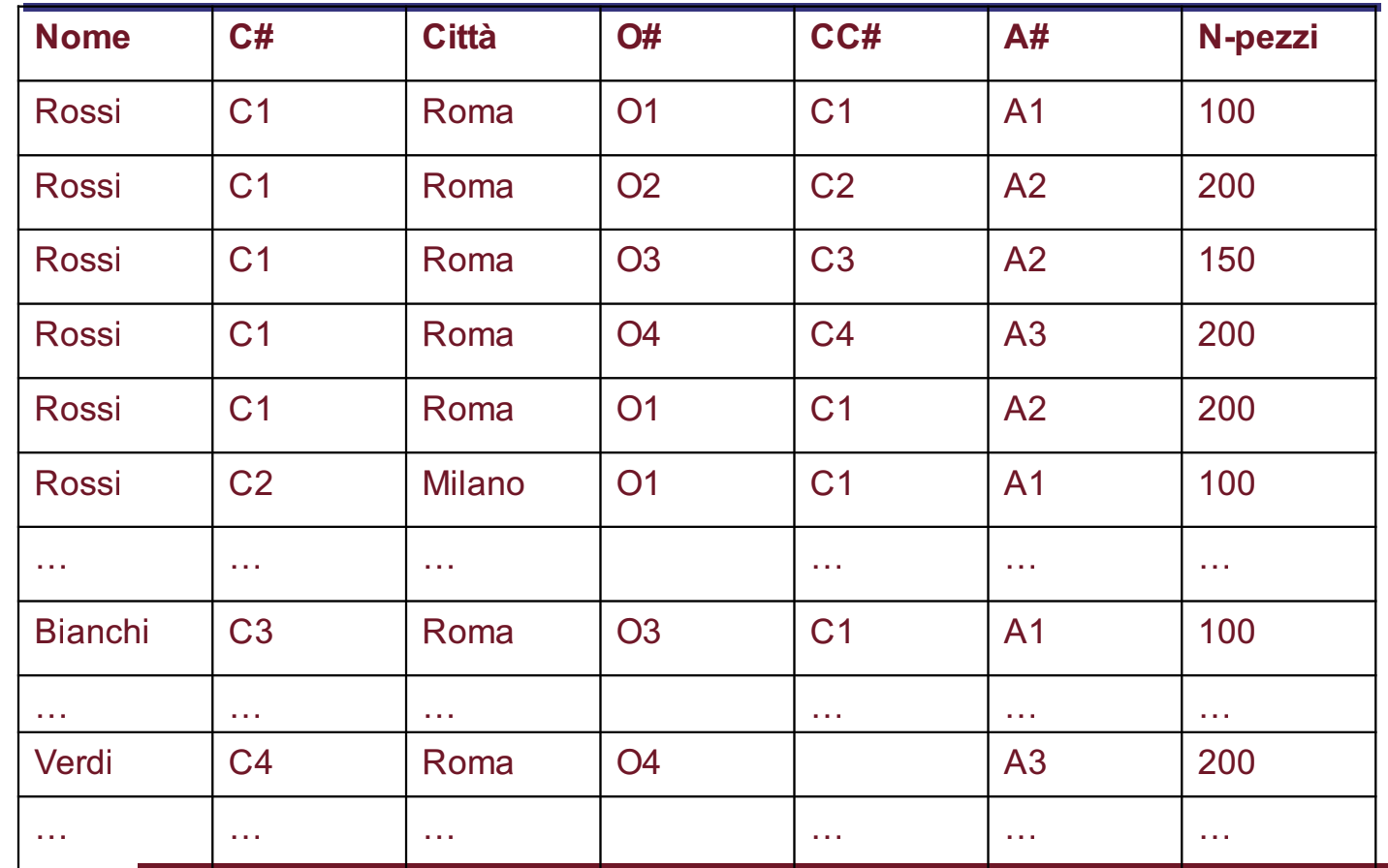
Adesso però abbiamo delle ennuple “inutili” dato che C# e CC# non corrispondono.

Per risolvere questo problema possiamo fare una selezione dove C# e C## sono uguali ottenendo:

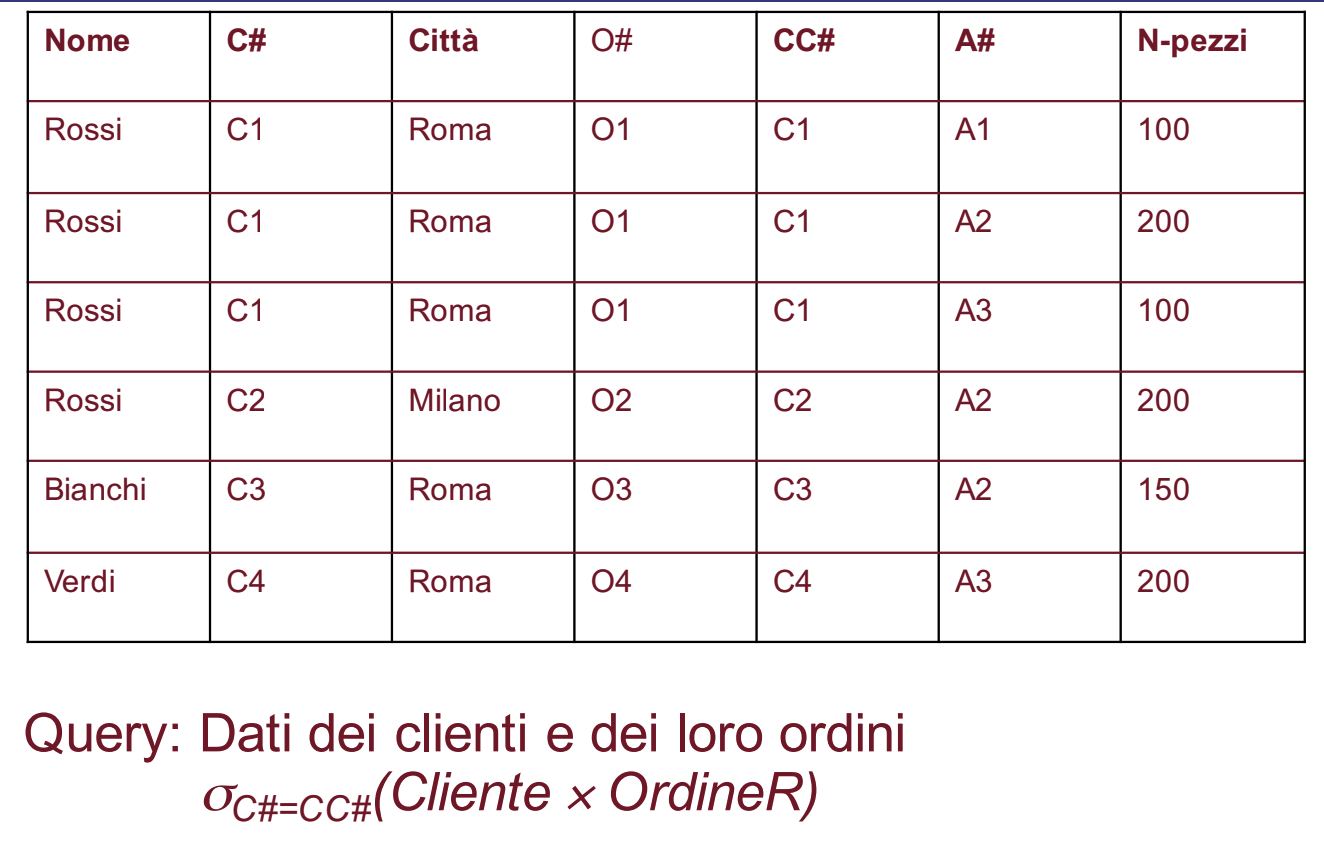
Notiamo anche che adesso le colonne C# e C## sono uguali, quindi se vogliamo fare una soluzione più elegante possiamo anche effettuare una proiezione sugli altri attributi e lasciare solo la colonna C#.

Join Naturale

Consente di selezionare le tuple del prodotto cartesiano dei due operandi che soddisfano la condizione:

R_{1} . A_{1} = R_{2} . A_{1} \land R_{1} . A_{2} = R_{2} . A_{2} \land \dots \land R_{1} . A_{k} = R_{2} . A_{k}

Dove $R_{1}$ ed $R_{2}$ sono i nomi delle relazioni operando e $A_{1} \dots A_{k}$ sono gli attrinuti comuni, cioè con lo stesso nome, delle relazioni operando, eliminando le ripetizioni degli attributi.

Si scrive con $r_{1} ▹ ◃ r_{2} = π_{X Y} (σ_{C} (r_{1} \times r_{2}))$

NOTA:

Nel join naturale gli attributi della condizione che consente di unire solo le ennuple giuste hanno lo stesso nome.
Vengono unite le ennuple in cui questi attributi hanno lo stesso valore

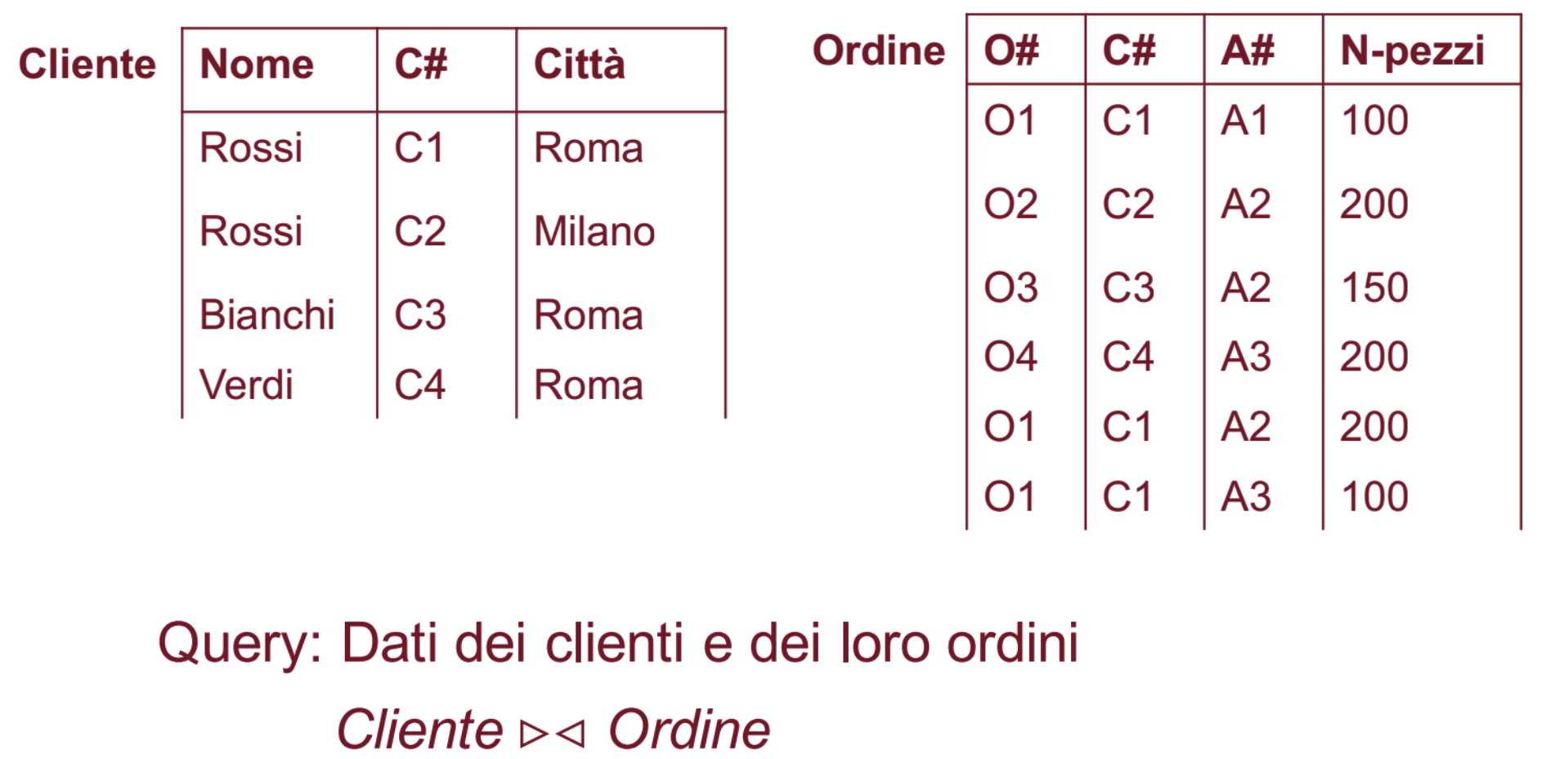
Quindi il Join naturale fa tutte le operazioni che abbiamo visto prima con il prodotto cartesiano.

Risultato Join:

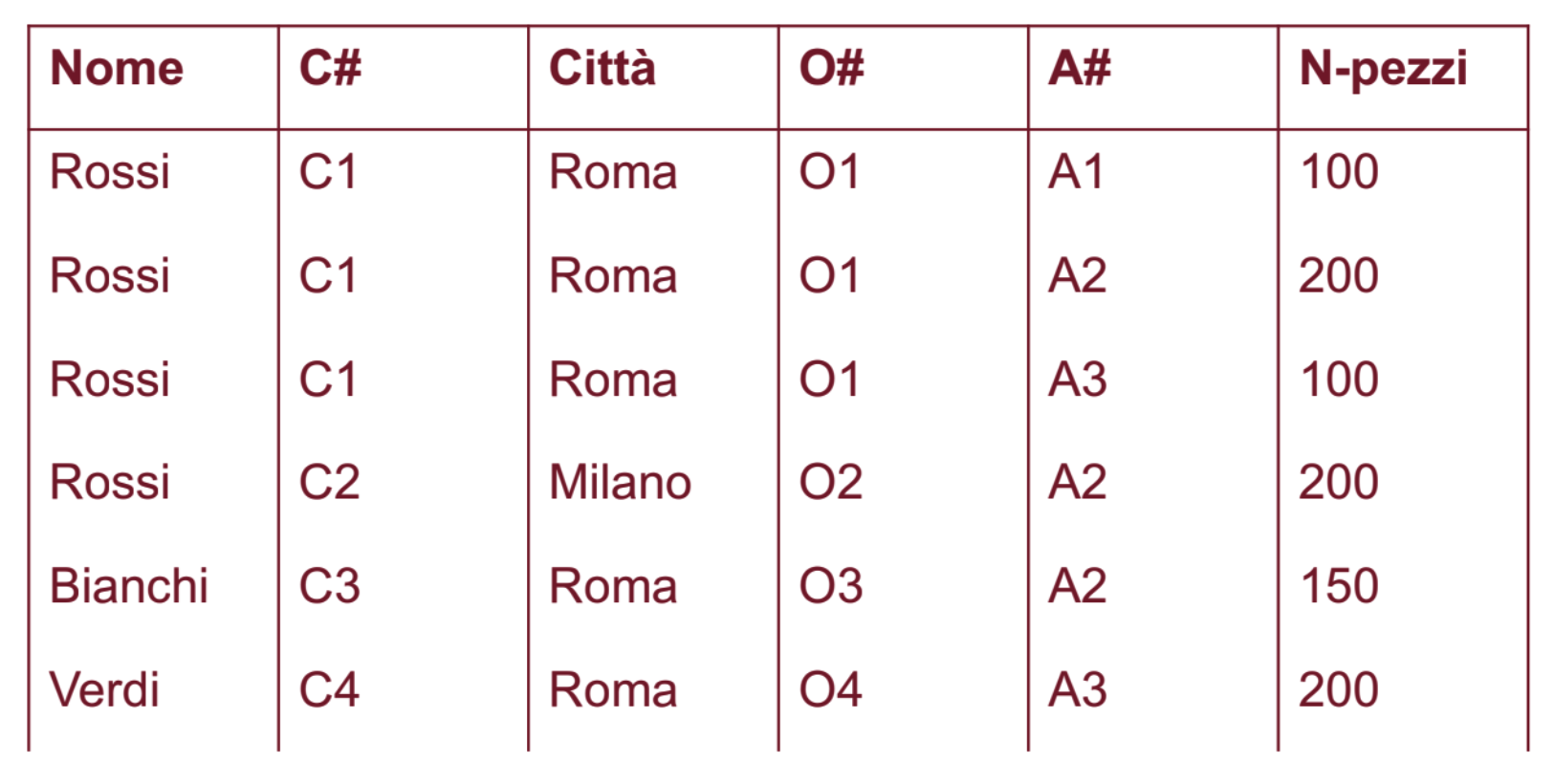
Spesso quando facciamo un join non vogliamo farlo su tutti gli attributi in comune ma solo su alcuni specificati, si vede successivamente con altri tipi di join.

Anche nel caso in cui gli attributi non hanno lo stesso nome, o come prima facciamo una ridenominazione oppure usiamo altri join, altrimenti in alcuni casi il join potrebbe restituire un prodotto cartesiano.

Casi Limite Join Naturale

Attributi con lo stesso nome ma nessuna tupla della prima relazione ha valori uguali con la seconda relazione in corrispondenza degli attributi uguali, risultato vuoto.

Se non abbiamo attributi con lo stesso nome, il risultato diventa un prodotto cartesiano.

Un possibile errore quindi può essere che gli attributi hanno lo stesso nome ma non lo stesso significato.

Quindi C# in Artista è il codice artista mentre in Quadro indica il codice quadro, il join per avere senso quindi deve essere effettuato tra Artista.C# e Quadro.Artista, non possiamo utilizzare un join naturale.

Possiamo o fare una ridenominazione o usare un $θ$ join.

$θ$ Join

Consente di selezionare le tuple del prodotto cartesiano di due operandi che soddisfano una condizione: $A θB$ .

Ci permette di effettuare un join sugli attributi che vogliamo noi.

Dove:

$θ$ è un operatore di confronto
A è un attributo della prima relazione
B è un attributo della seconda relazione
$d o m (A) = d o m (B)$

Ad es. $r_{1} A θB ▹ ◃ r_{2} = σ_{A θB} (r_{1} \times r_{2})$

Condizione Negative

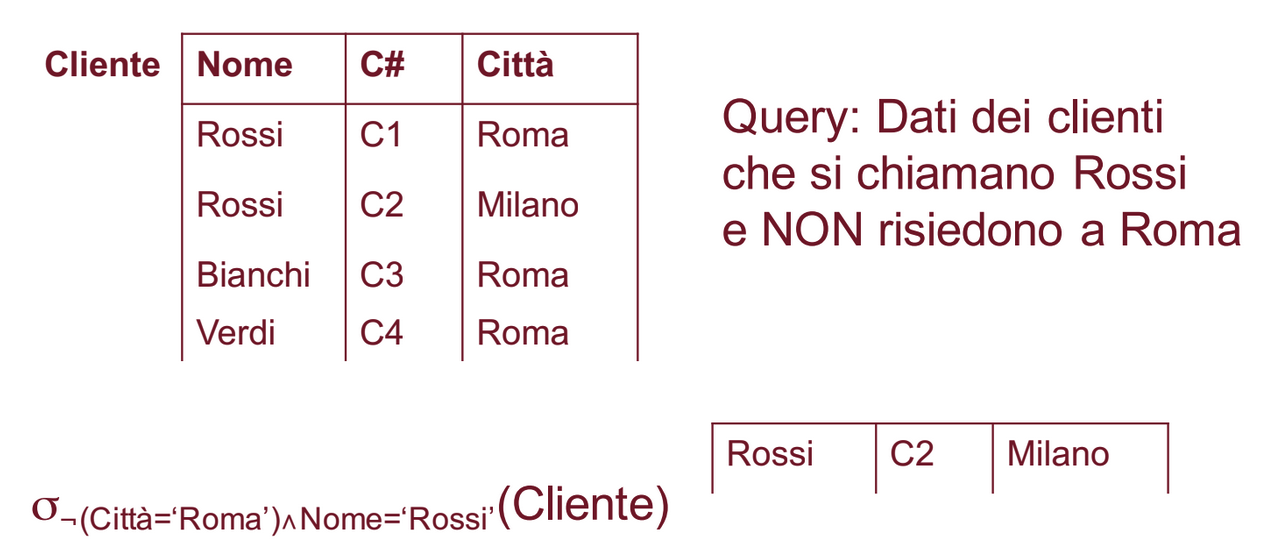
Quindi quando le informazioni che vogliamo non sono nella stessa relazione:

Troviamo tutte le relazioni che contengono le informazioni
Selezioniamo soltanto dei sottoinsiemi rilevanti per le interrogazioni
Combiniamo le informazioni attraverso i valori che in delle tuple fanno riferimento ad altre tuple

Quantificatore Universale

Fino ad ora abbiamo visto query che implicano condizioni equivalenti al quantificatore esistenziale $\exists$ ovvero “esiste almeno un”.

Era possibile rispondere a queste query dato che la valutazione delle tuple avviene in modo sequenziale quando si incontra una tupla che soddisfa la condizione si aggiunge al risultato.

La condizione però potrebbe richiedere la valutazione di gruppi interi di tuple prima di decidere se inserirerle o meno nel risultato, e le tuple una volta inserite non possono essere rimosse, in questo caso la query corrisponde al quantificatore universale $\forall$ oppure $\neq \exists$ .

Esempio

Notiamo che ad esempio la seconda tupla soddisfa la condizione di aver comprato più di 100 pezzi ma non possiamo inserirla, in qualche modo dovremmo memorizzare che “Rossi” compariva in una tupla precedente e non soddisfaceva la condizione.

Anche scambiando l’ordine delle tuple non risolviamo il problema, infatti lo inseriremo ma successivamente dovremmo toglierlo dal risultato.

Negazione del quantificatore universale

La negazione di “per ogni” non è “per nessuno” ma “esiste almeno un elemento per cui la condizione è falsa”.

Grazie a questo possiamo risolvere il problema con una doppia negazione:

Eseguiamo la query con la condizione negata
In questo modo abbiamo trovato gli oggetti che almeno una volta soddisfano la condizione contraria e quindi non soddisfano sempre quella che ci interessa.
Eliminiamo questi oggetti ottenuti dal totale tramite la differenza

Quindi in questo caso eseguiamo:

σ_{N - p ezz i \leq 100} (Cl i e n t e ⋈ O r d in e) Facciamo la proiezione sul nome e citt \overset{a}{ˋ} π_{N o m e, C i tt \overset{a}{ˋ}} (σ_{N - p ezz i \leq 100} (Cl i e n t e ⋈ O r d in e)) E abbiamo ottenuto chi non ci interessa π_{N o m e, C i tt \overset{a}{ˋ}} (Cl i e n t e ⋈ O r d in e) - π_{N o m e, C i tt \overset{a}{ˋ}} (σ_{N - p ezz i \leq 100} (Cl i e n t e ⋈ O r d in e))

In questo modo ci sono rimasti soltanto chi non ha mai ordinato meno di 100.

Nota

Se sappiamo di inserire un cliente nel struttura dati soltanto quando effettua un ordine allora nel primo operando della differenza potremmo scrivere semplicemente $π_{N o m e, C i tt \overset{a}{ˋ}} (Cl i e n t e)$ ovvero i clienti totali.

Ma se questo non è vero allora nel risultato finale avremo anche clienti che non hanno mai effettuato ordine, per questo abbiamo effettuato un join cliente, in modo da avere soltanto chi avesse almeno un ordine.

Inoltre è importante anche valutare le proiezioni, nell’esempio precedente ci interessavano i nomi ma abbiamo proiettato anche su Città, questo perché altrimenti nella sottrazione sarebbe sparito anche il Rossi di Milano.

Esempio

Seguendo lo stesso ragionamento di prima, prendiamo prima chi non ci interessa:

π_{N o m e, C i tt \overset{a}{ˋ}} (σ_{N - p ezz i > 100} (Cl i e n t e ⋈ O r d in e))

E poi eseguiamo una differenza:

π_{N o m e, C i tt \overset{a}{ˋ}} (Cl i e n t e ⋈ O r d in e) - π_{N o m e, C i tt \overset{a}{ˋ}} (σ_{N - p ezz i > 100} (Cl i e n t e ⋈ O r d in e))

La query in questo caso restituisce un risultato vuoto.

Condizioni che richiedono il prodotto di una relazione con se stessa

Ci sono anche casi in cui sono associati oggetti della stessa relazione.

Esempio

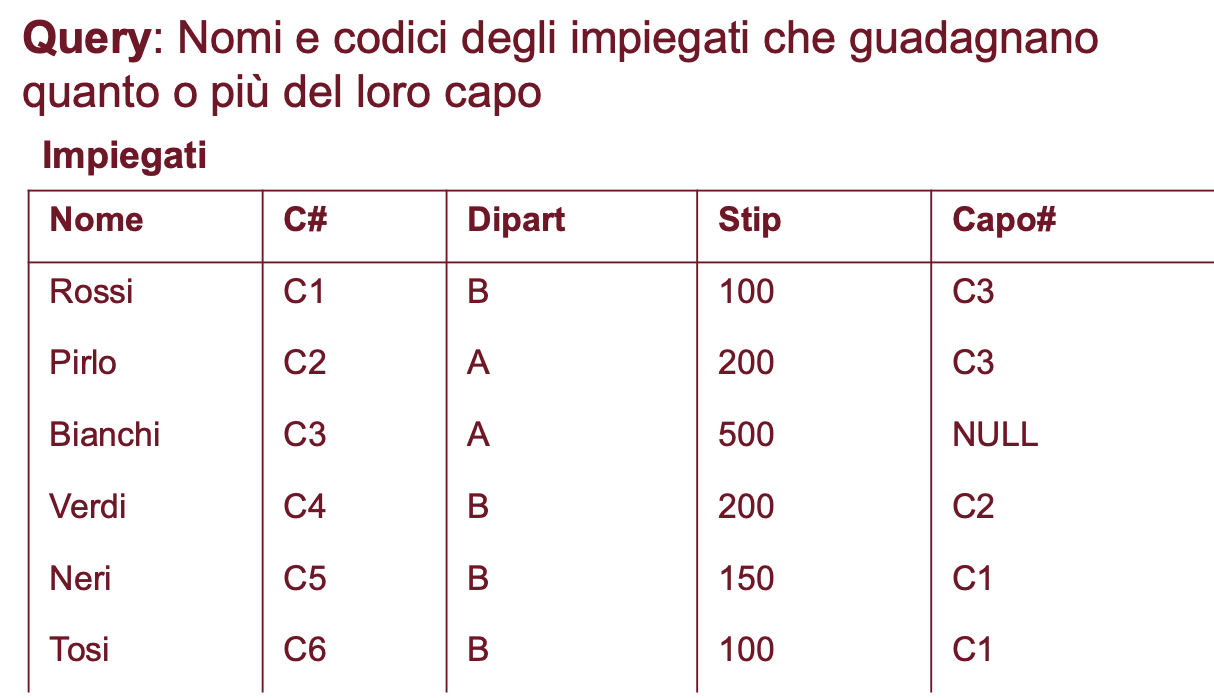
Le informazioni che ci servono sono tutte nella stessa relazione ma si trovano su tuple diverse e per poter confrontare valori, questi devono trovarsi sulla stessa tupla, come procediamo?

Creiamo una copia della relazione ed effettuiamo un prodotto in modo da combinare le informazioni di un impiegato con quelle del suo capo, quindi creiamo una relazione ImpiegatiC che con un join sarà collegata ad Impiegati combinando le tuple che hanno il valore C# uguale a Capo#. Utilizziamo anche la ridenominazione per aiutarci.

I m p i e g a t i C = p_{N o m e, C #, D i p a r t, St i p, C a p o # \leftarrow CN o m e, CC #, C d i p a r t, C s t i p, C c a p o #} (I m p i e g a t i)

Poi eseguiamo:

σ_{C a p o # = CC #} (I m p i e g a t i \times I m p i e g a t i C)

Ridenominazione

Se non avessimo usato la ridenominazione il join naturale ci avrebbe fatto combinare anche ogni impiegato con se stesso, inoltre C3 non ha capo quindi non entra nel join dal lato impiegato.

A questo punto ci basta confrontare gli stipendi e infine proiettare:

r = (σ_{St i p \geq CSt i p} (σ_{C a p o # = CC #} (I m p i e g a t i \times I m p i e g a t i C)))

π_{N o m e, C #} (r)

Esempio

Abbiamo come query: “Nomi e codici dei capi che guadagnano più di tutti i loro impiegati”.

Possiamo prendere la query dell’esempio precedente che trova gli impiegati che guadagnano quanto o più del loro capo, i capi che compaiono anche una sola volta in questo risultato non ci interessano.

r = (σ_{St i p \geq CSt i p} (σ_{C a p o # = CC #} (I m p i e g a t i \times I m p i e g a t i C)))

π_{CN o m e, CC #} (σ_{C a p o # = CC #} (I m p i e g a t i \times I m p i e g a t i C)) - π_{CN o m e, CC #} (r)

Note

Progettazione basi di dati - Problemi e Vincoli

Vogliamo creare una base di dati per studenti universitari che contiene:

Dati Anagrafici e identificativa:

Nome e cognome
Data, comune e provincia di nascita
matricola
codice Fiscale

Dati curriculari, per ogni esame:

Voto
data
codice, titolo e docente del corso

Ipotesi 1

Creiamo una sola relazione con schema:

Curriculum(Matr,CF,Cogn,Nome,DataN,Com,Prov,C#,Tit,Doc,DataE,Voto)

Che problemi si presentano?

Ridondanza:

I dati di uno studente vengono memorizzati ogni volta che questo sostiene un esame mentre i dati di un corso sono memorizzati per ogni esame sostenuto in quel corso, questo porta a spreco di memoria ed errori durante aggiornamento, inserimento e cancellazione.

Anomalia di Aggiornamento:

Se cambia il docente di un corso, dobbiamo cambiarlo per ogni esame sostenuto in quel corso, stessa cosa per ogni altro dato.

Anomalia di Inserimento:

Non posso inserire i dati di uno studente finché non ha sostenuto almeno uno esame, a meno che non inserisco molti valori NULL. Non posso comunque farlo dato che questi attributi fanno parte della chiave.

Anomalia di Cancellazione:

Se elimino i dati di uno studente sto cancellando anche i dati di un corso, se ad esempio lo studente è l’unico ad aver sostenuto l’esame di quel corso.

Tutti questi problemi accadono perché ho messo insieme 3 informazioni di oggetti diversi, corsi, esami e studenti.

Ipotesi 2

Possiamo passare quindi a tre schemi di relazione:

$Studente(Matr,CF,Cogn,Nome,Data,Com,Prov)$
$Corso(C#,Tit,Doc)$
$Esame(Matr,C#,Data,Voto)$

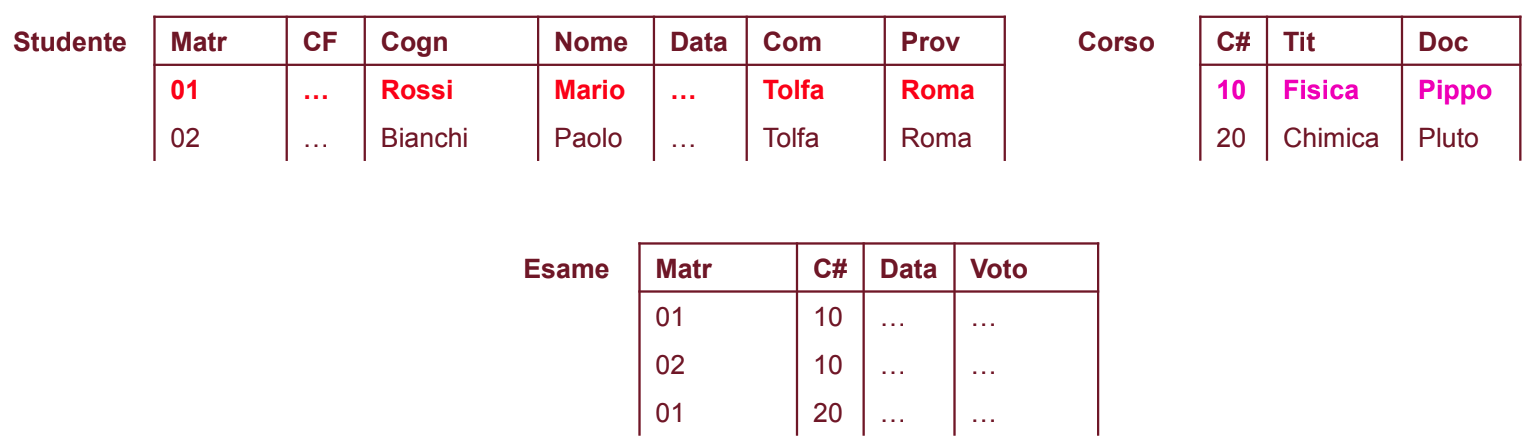
Non abbiamo i problemi di prima però se ne presenta un atro con Comune e Provincia dato che il Comune determina la Provincia

Ridondanza:

Il fatto che un comune si trova in una provincia è ripetuto molte volte

Anomalia di aggiornamento:

Se un comune cambia provincia devono essere modificate più tuple

Anomalia di Inserimento:

Non è possibile memorizzare il fatto che un comune si trova in una provincia se non abbiamo almeno uno studente di quel comune

Anomalia di Cancellazione:

Cancellando studenti potremmo perdere informazioni relative ai comuni

La base di dati adesso è formata da:

$Studente(Matr,CF,Cogn,Nome,Data,Com)$
$Corso(C#,Tit,Doc)$
$Esame(Matr,C#,Data,Voto)$
$Comune(Com, Prov)$

In questo modo non abbiamo più ridondanze e anomalie

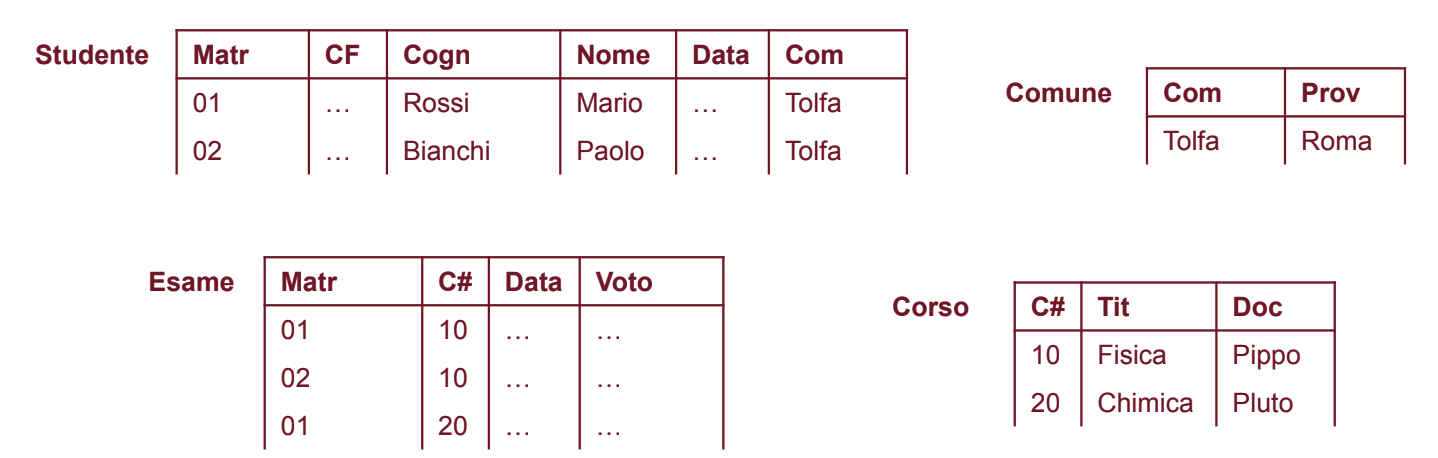
Schema "buono"

Uno schema è buono se non presenta ridondanza e anomalie di aggiornamento, inserimento e cancellazione, come si progetta? Occorre rappresentare ogni concetto in una relazione distinta

Rappresentazione dei concetti

Tutti i problemi di prima derivano dal fatto che abbiamo rappresentanto in un’unica relazione tre concetti diversi, 4 considerando anche i comuni e le province.

Vincoli

I vincoli sono delle condizioni sulla realtà che stiamo progettando, ad esempio:

Un voto va da 18 a 30
La matricola deve essere univoca
ecc..

Quando rappresentiamo una realtà deve essere possibili rappresentare anche tutti i suoi vincoli, un’istanza è legale se soddisfa tutti i vincoli imposti. Più avanti vedremo che per questa definizione ci interessano soltanto le dipendenze funzionali e non ad esempio i vincoli di dominio.

Un DBMS permette di:

Definire insieme allo schema della base anche i suoi vincoli
Verificare che un’istanza sia legale
Impedire l’inserimento di tuple che violerebbero tali vincoli

Le dipendenze funzionali di uno schema esprimono dei vincoli di dipendenza tra sottoinsiemi di attributi dello schema stesso, questi devono essere soddisfatti da ogni istanza dello schema. Se io ad esempio ho Matricola e CF nel caso di matricola uguale dovrà essere uguale anche CF.

Dipendenze Funzionali

Schema di relazione

Uno schema di relazione $R$ è un insieme di attributi ${A_{1}, \dots, A_{n}}$

Notazione:

$R = A_{1}, \dots, A_{n}$
Le prime lettere dell’alfabeto denotano singoli attributi
Le ultime lettere denotano insiemi di attributi
Se $X$ ed $Y$ sono insiemi di attributi $X Y$ denota $X \cup Y$

Tupla

Dato uno schema di relazione $R$ una tupla $t$ su $R$ è una funzione che associa ad ogni attributo $A$ in $R$ un valore $t [A_{i}]$ nel corrispondente $d o m (A_{i})$ .

Se $X$ è un sottoinsieme di $R$ e $t_{1}, t_{2}$ sono due tuple su $R$ , $t_{1} e t_{2}$ coincidono su $X$ se $\forall A \in X (t_{1} [A] = t_{2} [A])$ .

Istanza di Relazione

Dato uno schema di relazione $R$ una istanza di $R$ è un insieme di tuple su $R$

Dipendenze Funzionali

Dato uno schema di relazione $R$ , una dipendenza funzionale su $R$ è una coppia ordinata di sottoinsiemi non vuoti $X, Y$ di $R$ .

Notazione:

$X \to Y$
$X$ determina funzionalmente $Y$ oppure $Y$ dipende funzionalmente da $X$
$X$ = Determinante
$Y$ = Dipendente

Dati uno schema $R$ e una dipendenza funzionale $X \to Y$ su $R$ , un’istanza $r$ di $R$ soddisfa la dipendenza funzionale $X \to Y$ se:

\forall t_{1}, t_{2} \in r (t_{1} [X] = t_{2} [X] \Rightarrow t_{1} [Y] = t_{2} [Y])

Se $t_{1} [X] \neq = t_{2} [X]$ allora la dipendenza è comunque soddisfatta qualsiasi siano i valori di $t_{1} [Y], t_{2} [Y]$ .

Quindi notiamo che il minimo numero per violare una dipendenza è 2, infatti istanze da 1 o 0 elementi è impossibile che violino una qualsiasi dipendenza.

Istanza Legale

Dati uno schema di relazione $R$ e un insieme $F$ di dipendenze funzionali, un’istanza di $R$ è legale se soddisfa tutte le dipendenze in $F$ .

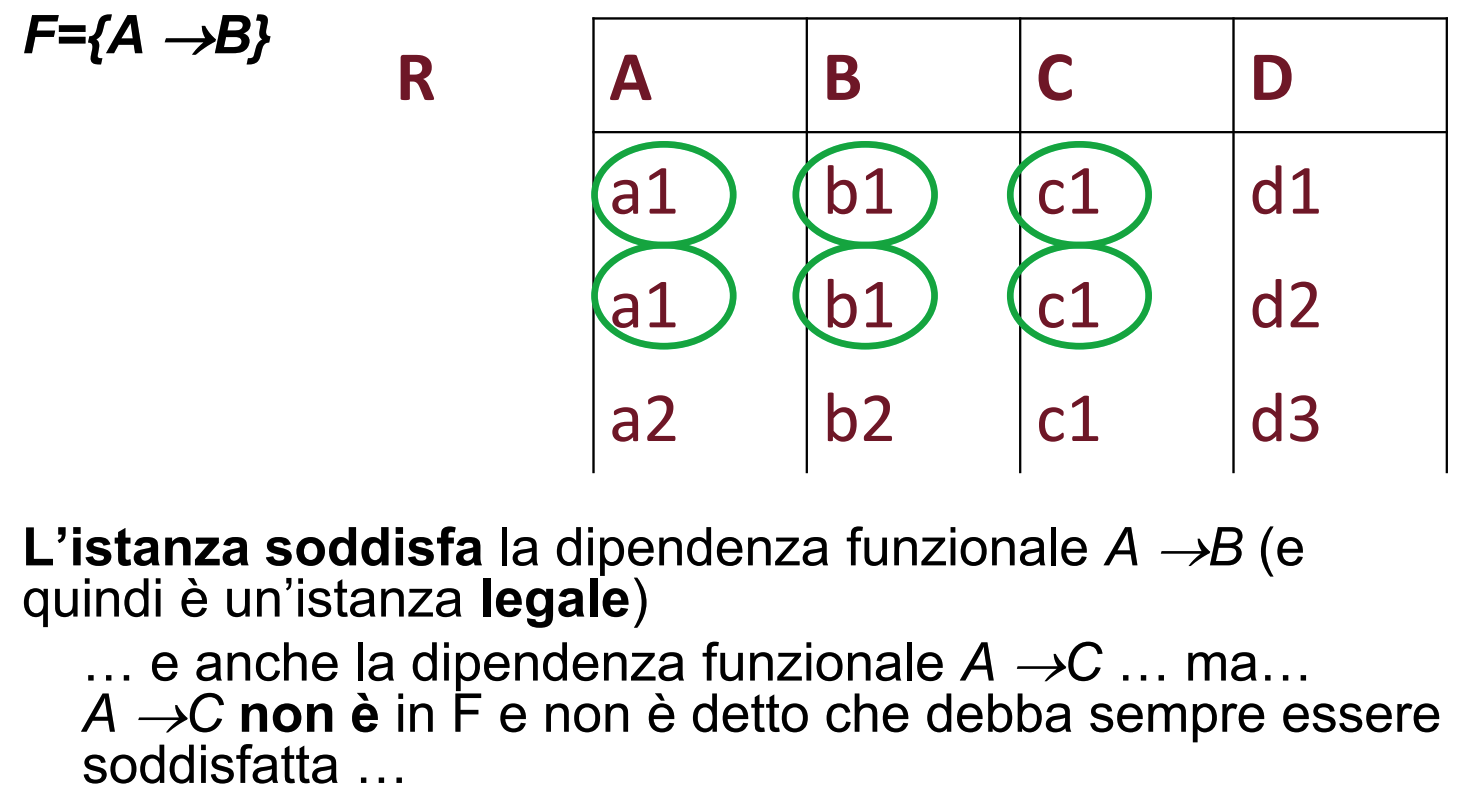
Osservazione

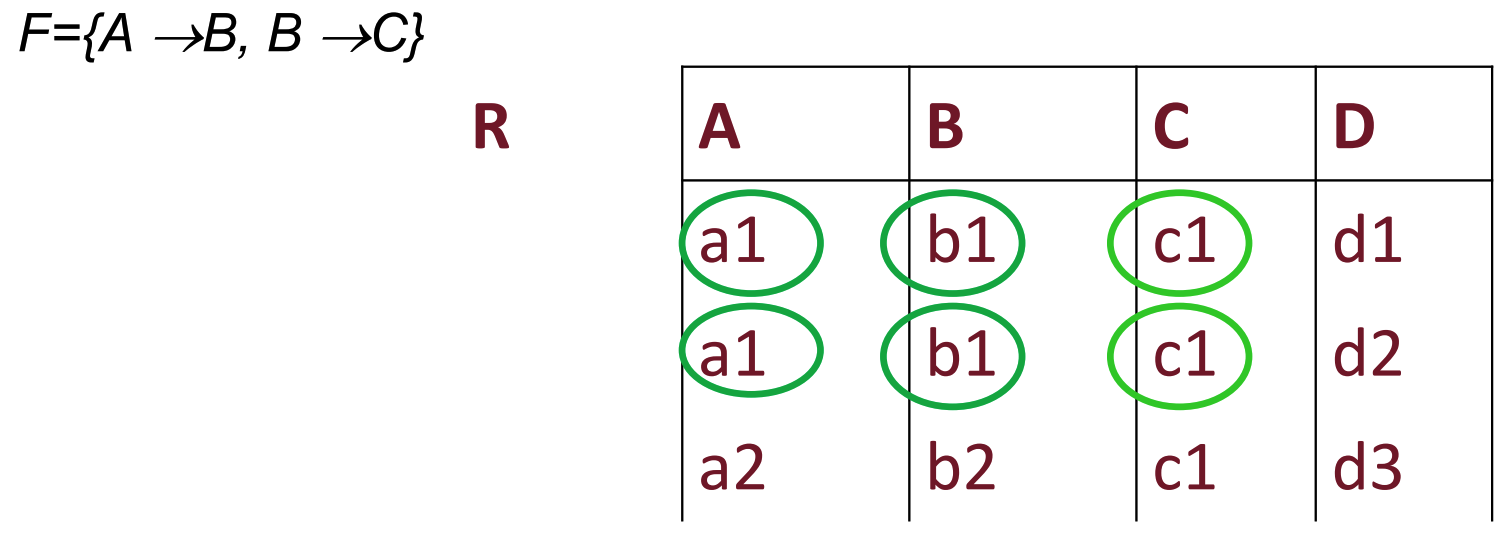
Notiamo che ogni istanza legale che quindi soddisfa $A \to B, B \to C$ soddisfa sempre anche la dipendenza $A \to C$ , possiamo quindi considerarla come se fosse in $F$ ?

Dato uno schema di relazione $R$ e un insieme $F$ di dipendenza funzionali su $R$ ci sono delle dipendenze funzionali che non sono in $F$ ma che sono comunque soddisfatte da tutte le istanze legali di $R$ .

Chiusura di un insieme di Dipendenze Funzionali

Dato uno schema di relazione $R$ e un insieme $F$ di dipendenze funzionali su $R$ la chiusura di $F$ è l’insieme delle dipendenze funzionali che sono soddisfatte da ogni istanza legale di $R$ .

Lo scriviamo $F^{+}$ .

Otteniamo quindi che $F \subseteq F^{+}$ .

Chiave

Dati uno schema di relazione $R$ e un insieme di dipendenze funzionali $F$ , un sottoinsieme $K$ di uno schema di relazione $R$ è una chiave se:

$K \to R \in F^{+}$
Non esiste un sottoinsieme proprio $K^{'}$ di $K$ tale che $K^{'} \to R \in F^{+}$

Se rispettiamo soltanto la prima condizione allora $K$ è detta superchiave. Se soddisfa la seconda e quindi non ha altri sottoinsiemi che soddisfano la prima condizione allora è detta chiave. Possiamo anche diri quindi che una chiave è sempre superchiave dato che contiene se stessa ma una superchiave non è detto che sia sempre chiave, ma ne contiene sempre una.

$K \to R$ significa che se due tuple sono uguali su $K$ allora le tuple devono essere uguali e dato che non possiamo avere due tuple uguali significa che non possiamo avere due chiavi uguali.

Esempio

Consideriamo lo schema $Studente = (Matr, Cognome, Nome, Data)$ . Il numero di matricola viene assegnato allo studente per identificarlo e quindi non ci possono essere 2 studenti con la stessa matricola e un’istanza di Studente non può contenere due tuple con lo stesso numero di matricola.

Otteniamo quindi che $Matr \to Matr, Cognome, Nome, Data$ deve essere soddisfatta da ogni istanza legale. Matr è chiave per lo schema Studente.

Chiave Primaria

Dati uno schema $R$ e un insieme $F$ di dipendenze funzionali, possono esistere più chiavi, in SQL una di esse verrà scelta come chiave primaria (non può avere valore nullo).

Di solito si sceglie quella con meno attributi (non minimale, minimale significa che non ha altri sottoinsiemi chiave, superchiave) questo perché migliora la velocità di ricerca nella base di dati. Quindi una volta scelta chiave primaria le altre chiavi devo impostarle come attributi unique per rispettare il fatto che non si deve ripetere.

Dipendenze Funzionali Banali

Dati uno schema di relazione $R$ e due sottoinsiemi non vuoti $X, Y$ di $R$ tali che $Y \subseteq X$ si ha che ogni istanza $r$ di $R$ soddisfa la dipendenza funzionali $X \to Y$ .

Queste dipendenze sono soddisfatte da ogni tupla anche da quelle non legali.

Quindi ad esempio se io ho due tuple uguali su $X = A BC$ allora saranno uguali anche su $Y = A B$ e quindi $X \to Y$ è soddisfatta.

Quindi se $Y \subseteq X$ , $X \to Y \in F^{+}$ , questa è detta dipendenza banale.

Proprietà delle dipendenze funzionali

Dati uno schema di relazione $R$ e un insieme di dipendenze funzionali $F$ si ha:

X \to Y \in F^{+} \Leftrightarrow \forall A \in Y (X \to A \in F^{+})

Quindi se $A \to BC \in F^{+}$ allora anche $A \to B \in F^{+}$ e $A \to C \in F^{+}$ .

Per la terza forma normale l’insieme $F^{+}$ è molto importante, è l’insieme di tutte le dipendenze soddisfatte da tutte le istanze legali. Ma come si calcola questo insieme $F^{+}$ ?

Dato che calcolare $F^{+}$ è molto “pesante” ci limiteremo a capire se una dipendenza ne fa parte o meno.

Assiomi di Armstrong

Introduciamo $F^{A}$ , con gli Assiomi di Armstrong

Denotiamo $F^{A}$ come l’insieme di dipendenze funzionali definito:

Se $f \in F$ allora $f \in F^{A}$
Se $Y \subseteq X \subseteq R$ allora $X \to Y \in F^{A}$ Assioma della Riflessività
Se $X \to Y \in F^{A}$ allora $XZ \to Y Z \in F^{A}$ , per ogni $Z \subseteq R$ , Assioma dell’aumento
Se $X \to Y \in F^{A}$ e $Y \to Z \in F^{A}$ allora $X \to Z \in F^{A}$ , Assioma della transitività

Dimostreremo che $F^{+} = F^{A}$ , ma prima alcune osservazioni su questi assiomi:

Riflessività: Se $Y \subseteq X \subseteq R$ allora $X \to Y \in F^{A}$

Ad esempio $Nome \subseteq (Nome, Cognome)$ e quindi se due tuple hanno uguale la coppia (Nome, Cognome) allora avranno uguale l’attributo Nome e stesso ragionamento per Cognome. Questo significa che $(Nome,Cognome) \to Nome (o Cognome)$ è sempre soddisfatta.

Aumento: Se $X \to Y \in F^{A}$ allora $XZ \to Y Z \in F^{A}$ , per ogni $Z \subseteq R$

Ad esempio $CodiceFiscale \to Cognome$ è soddisfatta quando tutte le tuple che hanno lo stesso CodiceFiscale hanno anche lo stesso Cognome.

Se aggiungiamo un altro attributo Indirizzo avremo che se due tuple sono uguali su (CodFiscale, Indirizzo) lo saranno anche su (Cognome, Indirizzo), quindi se viene soddisfatta $CodFiscale \to Cognome$ viene soddisfatta anche $CodFiscale,Indirizzo \to Cognome,Indirizzo$ .

Transitività: Se $X \to Y \in F^{A}$ e $Y \to Z \in F^{A}$ allora $X \to Z \in F^{A}$

Ad esempio $Matricola \to CodFiscale$ è soddisfatta quando tutte le tuple con la stessa Matricola hanno anche lo stesso CodFiscale.

$CodFiscale \to Cognome$ è soddisfatta quando tutte le tuple con stesso CodFiscale hanno anche lo stesso Cognome.

Se entrambe le dipendenze sono soddisfatte quindi possiamo dire che ogni volta che le tuple hanno la stessa Matricola avranno hanno lo stesso Cognome, è soddisfatta quindi anche la dipendenza $Matricola \to Cognome$ .

Vediamo altre regole che ci permettono di derivare altre dipendenze in $F^{A}$ :

Se $X \to Y \in F^{A}$ e $X \to Z \in F^{A}$ allora $X \to Y Z \in F^{A}$ , Regola dell’unione
Se $X \to Y \in F^{A}$ e $Z \subseteq Y$ allora $X \to Z \in F^{A}$ , Regola della decomposizione
Se $X \to Y \in F^{A}$ e $WY \to Z \in F^{A}$ allora $W X \to Z \in F^{A}$ , Regola della pseudotransitività

Teorema: Sia $F$ un insieme di dipendenze funzionali dove valgono le implicazioni viste sopra.

Dimostrazione 1)

Se $X \to Y \in F^{A}$ per l’assioma dell’aumento si ha $X \to X Y \in F^{A}$ (aggiungiamo X da entrambe le parti quindi XX=X). Analogamente $X \to Z \in F^{A}$ diventa $X Y \to Y Z \in F^{A}$ e quindi per transitività si ha che $X \to Y Z \in F^{A}$ .

Dimostrazione 2)

Se $Z \subseteq Y$ allora per riflessività si ha $Y \to Z \in F^{A}$ . Quindi poiché $X \to Y \in F^{A}$ e $Y \to Z \in F^{A}$ per transitività $X \to Z \in F^{A}$

Dimostrazione 3)

Se $X \to Y \in F^{A}$ per aumento si ha $W X \to WY \in F^{A}$ , quindi dato che $W X \to WY \in F^{A}$ e $WY \to Z \in F^{A}$ allora per transitività abbiamo $W X \to Z \in F^{A}$ .

Osservazione

Da riscrivere

Chiusura di un insieme di attributi

Siano $R$ uno schema di relazione, $F$ un insieme di dipendenze funzionali su $R$ e $X$ un sottoinsieme di $R$ .

La chiusura di $X$ rispetto ad $F$ denotata con $X_{F}^{+}$ o anche $X^{+}$ è definito da:

X_{F}^{+} = {A ∣ X \to A \in F^{A}}

Fanno parte della chiusura, gli attributi che vengono determinati direttamente da $X$ (da dipendenze che sono in $F$ ), oppure indirettamente (da dipendenze che sono in $F^{A}$ ). Quindi otteniamo che:

X \subseteq X_{F}^{+} Riflessivit \overset{a}{ˋ}

Quindi in ogni istanza legale se due tuple sono uguali su $X$ allora sono uguali su tutti gli attributi della chiusura di $X$ , ovviamente se $F^{A} = F^{+}$ .

Chiusure

La chiusura di $F$ non è mai vuota dato che abbiamo sempre almeno le dipendenze banali stessa cosa per la chiusura di $X$ , infatti $X$ determina sicuramente se stesso.

Lemma:

Siano $R$ uno schema di relazione ed $F$ un insieme di dipendenze funzionali su $R$ si ha che: $X \to Y \in F^{A}$ se e solo se $Y \subseteq X^{+}$

Dimostrazione

Sia $Y = A_{1}, A_{2}, \dots, A_{n}$

PARTE SE:

Poiché $Y \subseteq X^{+}$ per ogni $i, i = 1, \dots, n$ si ha che $X \to A_{i} \in F^{A}$ , pertanto per la regola dell’unione $X \to Y \in F^{A}$

PARTE SE E SOLO SE

Poiché $X \to Y \in F^{A}$ per la regola della decomposizione si ha che per ogni $i, i = 1, \dots, n, X \to A_{i} \in F^{A}$ cioè $A_{i} \in X^{+}$ per ogni $i, i = 1, \dots, n$ e quindi $Y \subseteq X^{+}$ .

Teorema $F^{+} = F^{A}$

Siano $R$ uno schema di relazione ed $F$ un insieme di dipendenze funzionali su $R$ si ha $F^{+} = F^{A}$ .

Dimostrazione, dobbiamo dimostrare che $F^{A} \subseteq F^{+} \land F^{+} \subseteq F^{A}$ . La parte a sinistra ci indica che tutte le dipendenze calcolate con Armstrong sono soddisfatte dalle istanze, mentre a sinistra che tutte le dipendenza soddisfatte dalle istanze sono calcolabili con Armstrong.

Iniziamo dimostrando $F^{A} \subseteq F^{+}$ , Sia $X \to Y$ una dipendenza funzionale in $F^{A}$ , dimostriamo che $X \to Y \in F^{+}$ per induzione sul numero $i$ di applicazioni degli assiomi di Armstrong.

Base dell’induzione: $i = 0$ , in questo caso $X \to Y$ è in $F$ e quindi $X \to Y \in F^{+}$ , questo perché appunto non abbiamo applicato nessun assioma e $F \subseteq F^{+}$ . Inoltre questo significa che $X \to Y \in F^{+}$ significa che è rispettata da ogni istanza legale.

Ipotesi Induttiva: $i > 0$ , Prendiamo $i - 1$ applicazioni e per ipotesi induttiva abbiamo $X \to Y \in F^{A} \Rightarrow X \to Y \in F^{A}$

Passo Induttivo: Ci troviamo a $i - 1$ e per ipotesi ogni dipendenza ottenuta da $F$ applicando gli assiomi fino a $i - 1$ si trova in $F^{+}$ dobbiamo dimostrarlo anche per $i$ e si possono presentare 3 casi, ovvero l’applicazioni di ognuno dei 3 assiomi:

Riflessività

All’i-esimo passo decidiamo di applicare la riflessività, quindi se $X \to Y$ è stata ottenuta per riflessività allora implica che $Y \subseteq X$ .
$\forall r (l e g a l e) se t_{1} [X] = t_{2} [X] \Rightarrow t_{1} [Y] (Y \subseteq X) = t_{2} [Y] \Rightarrow X \to Y \in F^{+}$
Aumento

Se $X \to Y$ è stata ottenuta per aumento, quindi in $i - 1$ passi avevamo $V \to W \in F^{+}, F^{A}$ al quale possiamo applicare l’aumento con $Z$ ottenendo $V Z \to W Z \in F^{A}$ e possiamo chiamare $V Z = X$ e $W Z = Y$ .
$\forall r (l e g a l e) t_{1} [X] = t_{2} [X] \Rightarrow t_{1} [V Z] = t_{2} [V Z] \Rightarrow t_{1} [V] = t_{2} [V] \land t_{1} [Z] = t_{2} [Z] Per ipotesi so che V \to W \in F^{+} e quindi t_{1} [V] = t_{2} [V] \Rightarrow t_{1} [W] = t_{2} [W] t_{1} [W] = t_{2} [W] \land t_{1} [Z] = t_{2} [Z] \Rightarrow t_{1} [W Z] = t_{2} [W Z] \Rightarrow t_{1} [Y] = t_{2} [Y]$
Essendo quindi soddisfatta da ogni istanza legale abbiamo che la nuova dipendenza è in $F^{+}$ .
Transitività

$X \to Y \in F^{A}$ è stata ottenuta per transitività quindi a $i - 1$ $X \to Z \in F^{A} \Rightarrow Z \to Y \in F^{A}$ . E per ipotesi induttiva si trovano in $F^{+}$ quindi:
$\forall r (l e g a l e) t_{1} [X] = t_{2} [X] \Rightarrow t_{1} [Z] = t_{2} [Z] \Rightarrow t_{1} [Y] = t_{2} [Y]$

Quindi qualunque sia il numero di applicazioni di Armstrong, ogni dipendenza di $F^{A}$ si troverà anche in $F^{+}$ .

Adesso dobbiamo dimostrare che se una dipendenza si trova in $F^{+}$ allora si trova in $F^{A}$ . $F^{+} \subseteq F^{A}$ ovvero:

X \to Y \in F^{+} \Rightarrow X \to Y \in F^{A}

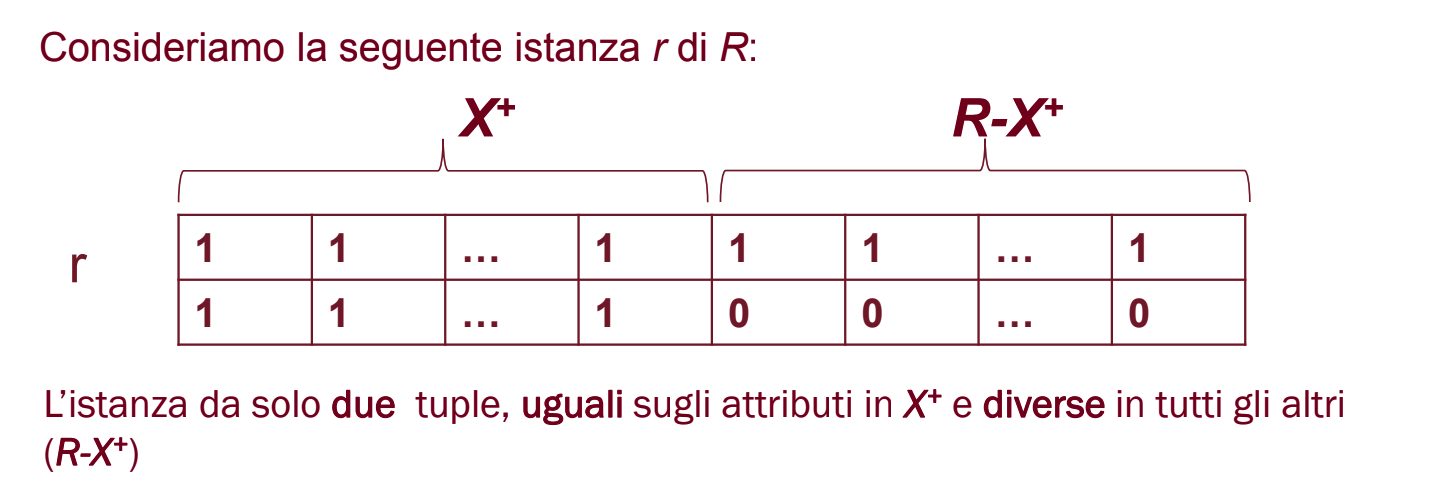
Prendiamo una qualunque dipendenza $V \to W \in F$ e mostriamo per prima cosa che $r$ è un’istanza legale perché la soddisfa:

Se $t_{1} [V] \neq = t_{2} [V]$ ovvero se $V \cap R - X^{+} \neq = \emptyset$ allora è soddisfatta.

Se $t_{1} [V] = t_{2} [V] \Rightarrow V \subseteq X^{+}$ (sappiamo che sono uguali sicuramente solo in $X^{+}$ ). Per il lemma 1 sappiamo che $V \subseteq X^{+} \Rightarrow X \to V \in F^{A}$ e per transitività insieme a $V \to W \in F \Rightarrow X \to W \in F^{A} Lemma 1 \Rightarrow W \subseteq X^{+} \Rightarrow t_{1} [W] = t_{2} [W]$ . Quindi le due tuple sono uguali sia sui valori di $V$ che su quelli di $W$ . L’istanza è legale.

Adesso mostriamo che se $X \to Y \in F^{+}$ allora $X \to Y \in F^{A}$ .

Dato che è un’istanza legale significa che $X \to Y \in F^{+}$ , quindi se $t_{1} [X] = t_{2} [X] \Rightarrow t_{1} [Y] = t_{2} [Y]$ , noi sappiamo che le tuple sono uguali per gli attributi di $X^{+}$ e per riflessività $X \subseteq X^{+}$ , quindi le tuple sono sicuramente uguali sui valori di $X$ e quindi l’implicazione ci dice che lo sono anche sui valori di $Y$ .

Se sono uguali sui valori di $Y$ significa che anche $Y \subseteq X^{+}$ e per il lemma che $X \to Y \in F^{A}$ .

Adesso abbiamo un modo per conoscere tutte le dipendenze in $F^{+}$ , queste sono le stesse che si possono inserire in $F^{A}$ partendo da $F$ e applicando gli assiomi di Armstrong e le regole derivate, notiamo però che abbiamo una complessità esponenziale e quindi calcolare questi insiemi richiede molto tempo.

Vedremo la terza forma normale che si basa come già detto sul fatto di decomporre il nostro schema e non rappresentare più concetti in un’unica tabella, ovviamente tutte le dipendenza soddisfatte nei vecchi schemi devono essere soddisfatte anche nei nuovi, in poche parole devono essere preservate tutte le dipendenze in $F^{+}$ .

Prendiamo lo schema visto un po’ sopra degli studenti, la base consiste in quattro schemi:

Studente (Matr, CF, Cogn, Nome, Data, Com) Corso (C#, Tit, Doc) Esame (Matr, C#, Data, Voto) Comune (Com, Prov)

Dato che una matricola identifica univocamente uno studente, significa che ogni istanza per essere legale deve rispettare:

Matr \to Matr CF Cogn Nome Data Com

E allo stesso modo anche un $CF$ identifica univocamente uno studente pertanto sia Matr che CF sono chiavi di Studente.

Possiamo anche osservare che ci possono essere studenti che con lo stesso cognome hanno nome diverso, quindi alcune istanze di studente non soddisfano $C o g n \to N o m e$ . Possiamo dire che le uniche dipendenze funzionali non banali che devono essere soddisfatte da un’istanza legale sono del tipo:

K \to X

Dove $K$ contiene una chiave, in questo caso Matr o CF.

Guardando gli altri schemi notiamo che un esame viene registrato una sola volta e quindi ogni istanza di esame per essere legale deve rispettare:

Matr C# \to Data Voto

Notiamo però che uno studente può sostenere esami in date differenti e avere anche voti diversi in vari esami. Quindi abbiamo delle dipendenze che non vengono soddisfatte sempre:

M a t r \to D a t a

M a t r \to V o t o

Possiamo osservare anche che l’esame relativo ad un corso viene superato da diversi studenti in diverse date e con voti diversi, per cui alcune istanze non soddisfano:

C# \to Data C# \to Voto

La chiave dello schema Esame è quindi Matr C#.

Completiamo la definizione di terza forma normale, per ora sappiamo solo che tutte le dipendenze non banali che devono essere soddisfatte devono essere del tipo $K \to X$ dove $K$ contiene una chiave oppure $X$ è contenuto in una chiave.

Terza Forma Normale

Dati uno schema di relazione R e un insieme di dipendenze funzionali $F$ su $R$ , $R$ è in 3NF se:

\forall X \to A \in F^{+}, A \neq \in X

(Con $A \neq \in X$ escludiamo le dipendenze banali)

$A$ appartiene ad una chiave (si dice che è primo) Oppure
$X$ contiene una chiave (è una superchiave)

È sbagliato scrivere $\forall X \to A \in F$ perché poi non sapremmo come valutare dipendenze del tipo $X \to A B$ ovvero con 2 o più attributi a destra, infatti in $F^{+}$ una dipendenza del tipo $X \to A B$ possiamo scomporla in $X \to A$ e $X \to B$ .

E se cambio la condizione in $\forall X \to Y \in F$ non so come comportarmi, infatti in $Y$ potremmo avere sia attributi primi che non, dovremmo cambiare la condizione in modo tale che tutti gli elementi di $Y$ siano primi.

Esempio

$R = A BC D$ , $F = {A B \to C D, A C \to B D, D \to BC}$

Abbiamo come chiavi $A B, A C, A D$

$D \to BC$ ha come determinante un attributo che non è superchiave però se scomponiamo otteniamo $D \to B$ e $D \to C$ e notiamo che $B C$ appartengono a delle chiave, sono quindi primi, rispettiamo la 3NF.

Esempio 2

$R = A BC D$ $F = {A \to B, B \to C D}$

La chiave è $A$ , infatti per ogni istanza legale:

$t_{1} [A] = t_{2} [A]$ allora $t_{1} [B] = t_{2} [B]$ ma allora se $t_{1} [B] = t_{2} [B]$ implica che $t_{1} [C D] = t_{2} [C D]$
Quindi se $t_{1} [A] = t_{2} [A]$ allora $t_{1} [C D] = t_{2} [C D]$ e quindi $A \to C D \in F^{A}$
Per la regola dell’unione $A \to BC D \in F^{A}$ e sappiamo che $F^{A} = F^{+}$ e quindi $A \to R \in F^{+}$ , inoltre $A$ è un singleton e quindi $A$ è una chiave.
$A$ è l’unica chiave perché $B$ non determina $A$ e nè $C$ nè $D$ determinato attributi.

Vediamo se siamo in 3NF:

$A \to B$ va bene dato che $A$ è chiave.
$B \to C D$ dobbiamo studiare le dipendenze $X \to A$ con $A$ singleton, quindi passando ad $F^{+}$ possiamo studiare $B \to C$ e $B \to D$ , notiamo che $B$ non è superchiave e inoltre $C$ e $D$ non sono primi, non rispettiamo la 3NF.

Esempio 3

$R = A BC D$ $F = {A C \to B, B \to A D}$

La chiave è $A C$ per ogni istanza legale.

Se $t_{1} [A C] = t_{2} [A C]$ allora $t_{1} [B] = t_{2} [B]$
Se $t_{1} [B] = t_{2} [B]$ allora $t_{1} [A D] = t_{2} [A D]$
Quindi $A C \to A D \in F^{A}$
$A C \to A BC D \in F^{A}$ e quindi sapendo che $F^{A} = F^{+}$ possiamo scrivere $A C \to R \in F^{+}$ , $A C$ è chiave dato che $A$ e $C$ da soli non determinano altri attributi.
$BC$ è un’altra chiave e quindi infatti applicando l’aumento a $B \to A D$ otteniamo $BC \to A C D$ .
Anche $A BC$ è una chiave, o meglio una superchiave dato che contiene $A C$ e $BC$ che sono chiavi.

3NF?

$A C \to B$ è ok dato che $A C$ è superchiave.
$B \to A D$ scomponiamola in $B \to A$ e $B \to D$ abbiamo $B$ che non è superchiave in entrambi i casi però $A$ appartiene ad una chiave e quindi ok ma $D$ non appartiene a chiavi e quindi violiamo la 3NF.

Questo caso è utile con la “scappatoia” vista prima di scrivere $X \to Y$ per la definizione, infatti in questo caso come valutiamo $B \to A D$ ? abbiamo $A$ primo ma $D$ no, dovremmo dare definizioni più complesse per valutare ogni attributo a destra. Dato che possiamo applicare la decomposizione, è più semplice fare così.

Violare 3NF

Per violare la 3NF è sufficiente trovare anche una sola dipendenza che viola la condizione.

Dipendenze Parziali e Transitive

Dipendenze Parziali

Prendiamo come esempio $Curriculum(Matr, CF, Cogn, Nome, DataN, Com, Prov, C#, Tit, Doc, DataE, Voto)$ , dove le chiavi sono Matr e C# notiamo che ad un numero di matricola corrisponde un solo cognome otteniamo quindi che $Matr C# \to Cogn$ e questa dipendenza è una conseguenza di quella vista prima $Matr \to Cogn$ .

La dipendenza $Matr C# \to Cogn$ viene detta dipendenza parziale, vediamo la loro definizione formale:

Siano $R$ uno schema di relazione e $F$ un insieme di dipendenze funzionali su $R$ .

$X \to A \in F^{+} ∣ A \neq \in X$ è una dipendenza parziale su $R$ se $A$ non è primo ed $X$ è contenuto propriamente in una chiave di $R$ .

Per capirlo meglio abbiamo che l’attributo Cognome dipende parzialmente dalla chiave Matr C# ovvero non mi serve la chiave intera per determinarlo ma soltanto una parte della chiave, infatti Matr appartiene alla chiave.

Dipendenze Transitive

Prendiamo come esempio lo schema $Studente (Matr, CF, Cogn, Nome, Data, Com, Prov)$ che ha come chiave Matr e CF. Notiamo che ad un numero di matricola corrisponde un solo comune di nascita $Matr \to Com$ e che un comune si trova in una sola provincia $Com \to Prov$ , in conclusione possiamo dire che $Matr \to Prov$ ovvero che ad una matricola corrisponde una sola provincia.

Possiamo dire quindi che $Matr \to Prov$ è una conseguenza delle altre due dipendenze e $Com \to Prov$ è detta dipendenza transitiva, vediamo le definizione formale:

Siano $R$ uno schema di relazione e $F$ un insieme di dipendenze funzionali su $R$ :

$X \to A \in F^{+} ∣ A \neq \in X$ è una dipendenza transitiva su $R$ se $A$ non è primo e per ogni chiave $K$ di $R$ abbiamo che $X$ non è contenuto propriamente in $K$ e $K - X \neq = \emptyset$ .

In questo caso abbiamo che l’attributo provincia non dipende direttamente da una chiave, ma dipende transitivamente infatti $Matr \to Prov$ è una conseguenza di $Matr \to Com$ e $Com \to Prov$ , inoltre è importante ricordare che la dipendenza transitiva è quella che “causa” la transitività e quindi in questo caso $Com \to Prov$ .

Definizione Alternativa 3NF

Dato uno schema $R$ un insieme di dipendenze funzionali $F$ , $R$ è in 3NF se e solo se non ci sono attributi che dipendono parzialmente o transitivamente da una chiave, o meglio se non ci sono né dipendenze parziali né transitive

Definizioni a Confronto

Le due definizioni sono equivalenti, dimostriamolo.

Teorema: Siano $R$ uno schema di relazione e $F$ un insieme di dipendenze funzionali su $R$ . Uno schema $R$ è in 3NF se e solo se non esistono né dipendenze parziali né transitive in $R$ .

Dimostriamo partendo dal fatto che lo schema è in 3NF

Siamo in 3NF quindi $\forall X \to A \in F^{+}, A \neq \in X$ , $A$ appartiene ad una chiave oppure $X$ contiene una chiave.

Se $A$ è parte di una chiave allora già è impossibile che ci siano dipendenze parziali o transitive, infatti questa è la prima condizione che devono rispettare entrambe. Se $A$ non è primo allora sappiamo che $X$ è superchiave, in quanto tale può contenere una chiave ma non essere contenuto propriamente in una chiave quindi non possiamo avere dipendenze parziali. Inoltre sapendo che $X$ è superchiave non può verificarsi che per ogni chiave $K$ di $R$ non è contenuto propriamente in $K$ e $K - X = \emptyset$ infatti ne contiene almeno una completamente e quindi facendo la differenza otteniamo il vuoto.

Dimostriamo partendo dal fatto che non esistono dipendenze parziali e transitive

Quindi sappiamo che non esistono dipendenze parziali e transitive, supponiamo per assurdo che $R$ non sia 3NF allora in questo caso esiste una dipendenza funzionale $X \to A \in F^{+}$ tale che $A$ non è primo e $X$ non è una superchiave, dato che $X$ non è una superchiave abbiamo due casi:

Per ogni chiave $K$ di $R$ abbiamo che $X$ non è contenuto propriamente in $K$ (infatti X non ha chiavi) e $K - X \neq = \emptyset$ (non faremo mai la differenza con una chiave). In questo caso abbiamo che $X \to A$ è transitiva, otteniamo una contraddizione.
Esiste una chiave $K$ di $R$ tale che $X \subset K$ e quindi $X$ è contenuto in una chiave, significa quindi che $X \to A$ è una dipendenza parziale, otteniamo una contraddizione.

Uno schema 3NF come abbiamo visto è quindi preferibile ad uno non, quando ne progettiamo uno è bene quindi mantenere questa struttura. Quando si progetta uno schema ovvero nella fase di individuazione dei concetti da rappresentare, se questa progettazione viene fatta bene lo schema derivato sarà 3NF, altrimenti dovremmo procedere ad una fase di decomposizione per portarcelo, come abbiamo visto con l’esempio dell’università.

Uno schema che non è in 3NF infatti può essere decomposto in più modi in un insieme di schemi che invece rispettano la 3NF.

Vediamo un esempio semplice con lo schema $R=ABC$ con l’insieme $F = {A \to B, B \to C}$ questo non è in 3NF per via della dipendenza transitiva $B \to C$ dato che la chiave è $A$ . Possiamo però decomporre $R$ in:

$R1=AB$ e con $F = {A \to B}$
$R2=BC$ e $F = {B \to C}$ Oppure
$R1=AB$ e con $F = {A \to B}$
$R2=AC$ e $F = {A \to C}$

Entrambi gli schemi sono in 3NF, tuttavia la seconda soluzione non va bene, perché?

Consideriamo due istanze legali degli schemi ottenuti:

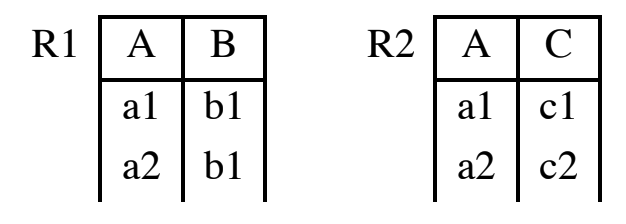
Ricostruiamo lo schema originale tramite un join naturale:

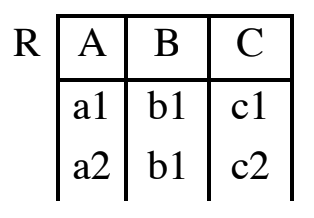
Notiamo che non è un’istanza legale di $R$ infatti non rispettiamo la dipendenza $B \to C$ , dobbiamo preservare tutte le dipendenze presenti in $F^{+}$ .

Vediamo un altro esempio.

Consideriamo lo schema $R = A BC$ con l’insieme di dipendenze funzionali $F = {A \to B, C \to B}$ , lo schema non è 3NF dato che entrambe le dipendenze sono parziali, la chiave infatti è AC e possiamo decomporre lo schema in:

$R 1 = A B$ con ${A \to B}$
$R 2 = BC$ con ${C \to B}$

Questo schema preserva tutte le dipendenze di $F^{+}$ ma non va comunque bene.

Prendiamo un’istanza legale di $R$

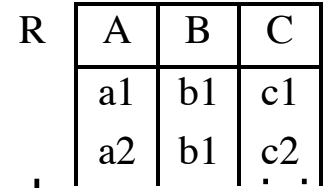
Adesso decomponiamola in base ai due schemi visti prima:

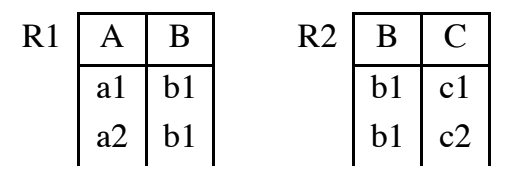
In teria facendo un join dovremmo ricostruire l’istanza originale ma non è così:

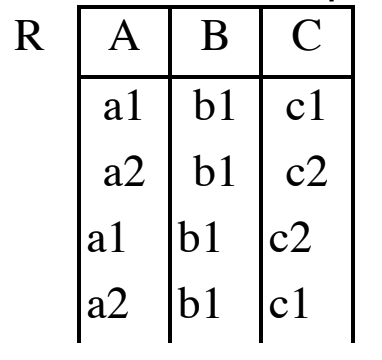
Le ultime due tuple sono estranee all’istanza originale, c’è stata quindi perdita di informazione.

Ci sono altri esempi nelle slide ma i casi sono uguali a questi due.

Per concludere quindi quando si decompone uno schema per ottenere una 3NF dobbiamo ricordare che:

Dobbiamo preservare le dipendenze funzionali che valgono sullo schema originario.
Dobbiamo permettere di ricostruire tramite join lo schema originario, senza aggiunta di informazioni estranee.

Formale Normale di Boyce-Codd

La 3NF non è la più restrittiva che possiamo ottenere, ne esistono altre come la forma normale di Boyce-Codd.

Definizione

Una relazione è in formale normale di Boyce-Codd (BCNF) quando ogni determinante è una superchiave.

Una relazione che rispetta BCNF è anche in terza formale normale, ma non è vero l’opposto.

Inoltre non è sempre possibile decomporre uno schema non BCNF e ottenere sottoschemi BCNF preservando allo stesso tempo tutte le dipendenze ma è sempre possibile per 3NF che va comunque bene.

Ci sono esempi su slide ma non so se sono utili, dato che prenderemo in considerazione solo 3NF da adesso

Chiusura di un Insieme di Attributi

Abbiamo detto che quando si decompone uno schema su cui è definito un insieme di dipendenze funzionali $F$ per ottenere altri schemi in 3NF, vogliamo preservare tutte le dipendenze e poter ricostruire tramite join tutta l’informazione originaria.

Si vogliono preservare tutte le dipendenze in $F^{+}$ quindi tutte quelle soddisfatte da ogni istanza legale, siamo quindi interessati a calcolare $F^{+}$ ma sappiamo che richiede tempo esponenziale in $∣ R ∣$ .

A noi basterà avere un metodo per decidere se una dipendenza funzionale $X \to Y$ appartiene ad $F^{+}$ , e possiamo farlo calcolando $X^{+}$ e verificando che $Y \subseteq X^{+}$ , infatti per il lemma: $X \to Y \in F^{A} \Leftrightarrow Y \subseteq X^{+}$ e poi il teorema dimostra che $F^{A} = F^{+}$ .

Il calcolo di $X^{+}$ può tornare utile a verificare che un insieme di attributi sia chiave di uno schema oppure verificare se una decomposizione preserva le dipendenze originarie. Vediamo come si calcola.

Calcolo di $X^{+}$

Per il calcolo della chiusura di un insieme di attributi $X$ denotata con $X^{+}$ possiamo utilizzare un algoritmo.

Come input abbiamo bisogno di uno schema di relazione $R$ , un insieme $F$ di dipendenze funzionali su $R$ e un sottoinsieme $X$ di $R$ .

Come output riceviamo la chiusura di $X$ rispetto ad $F$ restituita nella variabile $Z$ .

Z := X; S := {A / Y \to V \in F \land A \in V \land Y \subseteq Z} w hi l e S \neq \subset Z d o b e g in Z := Z \cup S; S := {A / Y \to V \in F \land A \in V \land Y \subseteq Z} e n d e n d

Quindi abbiamo $Z$ che è $X$ stesso, poi in $S$ inseriamo i singoli attributi che compongono le parti a destra delle dipendenze funzionali la cui parte sinistra è in $Z$ , quindi inizialmente in $S$ avremo gli attributi determinati da $X$ . Poi aggiungiamo questi elementi a $Z$ e continuiamo a iterare sui nuovi insieme $Z$ .

Ci fermiamo quando $S$ non ha elementi “nuovi” rispetto a $Z$ .

Esempio di applicazione

Notiamo che per ogni passaggio dobbiamo sempre far partire la catena di operazioni da $A B$ .

È quindi più semplice vedere cosa abbiamo in $Z$ e “combinando” i pezzi vedere cosa possiamo ottenere.

Adesso dobbiamo dimostrare che l’algoritmo è corretto, ovvero che calcola correttamente la chiusura di un insieme di attributi $X$ rispetto ad un insieme $F$ di dipendenze funzionali

Dimostrazione

Con $Z^{0}$ indichiamo il valore iniziale di $Z$ e con $Z^{i}$ e $S^{i}$ i valori di $Z$ ed $S$ dopo la i-esima iterazione Ad ogni iterazione aggiungiamo elementi in $Z$ , alla fine otteniamo $Z^{j}$ , dobbiamo provare che, siccome ad ogni iterazione non cancelliamo mai elementi ma al massimo ne aggiungiamo di nuovi, è facile notare che $Z^{i} \subseteq Z^{i + 1}$ per ogni $i$ .

Quindi sia $j$ tale che $S (j) \subseteq Z (j)$ , con $j$ indichiamo l’iterazione finale, proveremo che:

A \in Z^{(j)} \Leftrightarrow A \in X^{+}

Iniziamo mostrando che $A \in Z^{j} \Rightarrow A \in X^{+}$ , per induzione.

Base Induzione: $Z^{0}$ , sappiamo che questo è uguale ad $X$ ma $X \subseteq X^{+}$ e quindi $Z^{0} \subseteq X^{+}$ .

Ipotesi Induttiva: $Z^{i - 1} \subseteq X^{+} Lemma 1 \Rightarrow X \to Z^{i - 1} \in F^{A}$

Passo Induttivo: Prendiamo un attributo $A \in Z^{i} - Z^{i - 1}$ ovvero un attributo che abbiamo appena aggiunto. Se abbiamo aggiunto $A$ , significa che:

\exists Y \to W \in F : Y \subseteq Z^{i - 1} \land A \in W

Notiamo che $Y \subseteq Z^{i - 1} \subseteq X^{+}$ quindi possiamo scrivere che $Y \subseteq X^{+}$ e sempre per il lemma 1 $X \to Y \in F^{A}$ .

Adesso siccome abbiamo $X \to Y \in F^{A}$ e $Y \to W \in F$ , per transitività abbiamo che $X \to W \in F^{A}$ e per il lemma $W \subseteq X^{+}$ .

Adesso mostriamo che $A \in X^{+} \Rightarrow A \in Z^{j}$

Dato che abbiamo un $A \in X^{+}$ per il lemma sappiamo che $X \to A \in F^{+}$ quindi significa che questa dipendenza deve essere soddisfatta da ogni istanza legale.

Prendiamo come esempio la seguente istanza di $R$ :

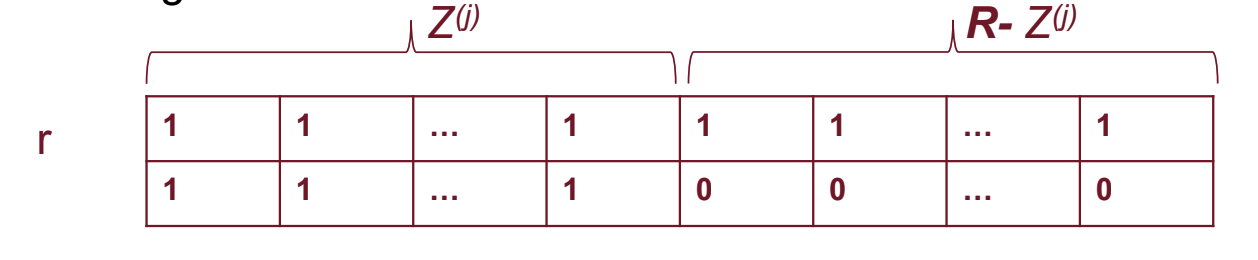
Mostriamo che è un’istanza legale.

Prendiamo una qualsiasi dipendenza $V \to W \in F$ e supponiamo per assurdo che non sia soddisfatta, questo significa che:

t_{1} [V] = t_{2} [V] e t_{1} [W] \neq = t_{2} [W]

Ovvero che:

V \subseteq Z^{j} e W \cap (R - Z^{j}) \neq = \emptyset

Ma questo significa che questo elemento che si trova ancora in $R - Z^{j}$ potrei raccoglierlo con l’algoritmo e portarlo dentro a $Z^{j + 1}$ in una nuova iterazione, ma questo significa che non abbiamo preso il “vero” $Z^{j}$ ovvero l’ultima iterazione e andiamo in contraddizione con la costruzione della nostra istanza.

Quindi la dipendenza $V \to W \in F$ è soddisfatta anche quando le tuple hanno valori uguali su $V$ , l’istanza è legale.

Dato che è legale soddisfa la nostra dipendenza $X \to A \in F^{+}$ , e dato che $X = Z^{0} \subseteq Z^{j}$ significa che le due tuple sono uguali su $X$ e quindi, siccome è legale, lo sono anche su $A$ ma questo significa che $A \in Z^{j}$ (per come abbiamo costruito l’istanza).

Insieme Vuoto

Ricordiamo che ${\emptyset}$ è diverso da $\emptyset$ , infatti il primo è un insieme che contiene l’insieme vuoto mentre il secondo è l’insieme vuoto stesso. Proprietà:

L’insieme vuoto è un sottoinsieme di ogni insieme $A$

L’unione di un qualunque insieme $A$ con l’insieme vuoto è $A$

L’intersezione di un qualunque insieme $A$ con l’insieme vuoto è l’insieme vuoto

L’unico sottoinsieme dell’insieme vuoto, è l’insieme vuoto stesso

L’insieme vuoto è finito ed ha 0 elementi

Identificare le chiavi di uno Schema

Per determinarle possiamo utilizzare il calcolo della chiusura di un insieme di attributi.

Esempio

Prendiamo lo schema $R = (A, B, C, D, E, H)$ e lo schema di relazioni:

F = {A B \to C D, C \to E, A B \to E, A BC \to D}

Calcoliamo la chiusura di $A B H$ , abbiamo che:

A B H \to C D A BC DH \to E E quindi A B H^{+} = A BC D E H = R

Ma $A B H$ è chiave? Ricordando la definizione abbiamo che un sottoinsieme $K$ di $R$ e un insieme di dipendenze funzionali $F$ è chiave se:

$K \to R \in F^{+}$
Non esiste un sottoinsieme proprio di $K$ che soddisfa la prima condizione

Quindi dobbiamo verificare che non ci siano sottoinsiemi di $A B H$ che siano chiave. Quindi utilizziamo ancora l’algoritmo delle chiusure sui sottoinsiemi di $K$ , facendo però alcune osservazioni:

Conviene partire da quelli con cardinalità maggiore, infatti se la loro chiusura non contiene $R$ è inutile proseguire con loro sottoinsiemi.
Gli attributi che non compaiono mai come dipendenti (a destra) faranno sicuramente parte della chiave, se invece compaiono sempre come dipendenti allora sicuramente non fanno parte della chiave.

Infatti prendendo l’esempio di prima, per vedere i sottoinsiemi di $A B H$ che sono chiavi possiamo dire per prima cosa che $H$ va sicuramente nella chiave dato che non viene mai determinato e quindi dobbiamo controllare i sottoinsiemi $A H, B H$ che sono quelli di cardinalità più grande.

Entrambi i sottoinsiemi non determinano altri attributi quindi possiamo fermarci qui, è inutile controllare sottoinsiemi di cardinalità inferiore, quindi $A B H$ è chiave.

In uno schema possiamo avere più chiavi

Abbiamo detto che $H$ deve essere sicuramente parte della chiave e abbiamo già verificato che $H, A H, B H$ non sono chiavi, proviamo a controllare $C H, DH, E H$ .

C H \to C H E

Quindi non è chiave.

DH \to DH

Non è chiave

E H \to E H

Non è chiave.

Quindi dovremmo provare con altri sottoinsiemi di 3 elementi, incluso $H$ , notiamo che $A, B$ da soli non determinano nulla e inoltre non dipendono da altri attributi quindi vanno per forza nella chiave. Questo significa che $A B H$ è l’unica chiave.

Per decidere da dove cominciare per cercare una chiave possiamo partire dalla osservazioni di prima, oppure si può cominciare dagli insiemi individuati dalle dipendenze funzionali: data una dipendenza $V \to W \in F$ calcoliamo la chiusura dell’insieme di attributi $X = R - (W - V)$ . Se la chiusura di questo insieme $X$ contiene $R$ allora $X$ è superchiave però dobbiamo verificare che sia chiave e quindi controllare i suoi sottoinsiemi.

Esempio

Abbiamo $R = {A, B, C, D, E}$ e:

F = {A B \to C, A C \to B, D \to E}

Quindi in base a quanto detto prima calcoliamo le superchiavi:

A BC D E - (C - A B) = (A B D E)^{+} = R A BC D E - (B - A C) = (A C D E)^{+} = R A BC D E - (E - D) = (A BC D)^{+} = R

Adesso però dobbiamo verificare che siano chiavi:

Notiamo che $A, D$ vanno sicuramente nella chiave
$A$ da solo non determina nulla quindi va sicuramente insieme a $C$ o $B$

Proviamo a vedere quindi $A D C$ e $A D B$ .

A D C \to BE \overset{e}{ˊ} chiave A D B \to CE \overset{e}{ˋ} chiave

Quindi $A B D E$ e $A BC D$ non sono chiavi dato che contengono $A B D$ mentre $A C D E$ non è chiave dato che contiene $A D C$ .

Per le osservazioni di prima è inutile controllare sottoinsiemi, non esistono. Dobbiamo avere sicuramente $D$ e $A$ non può stare da solo.

Test di unicità della chiave

Calcoliamo la chiusura dell’intersezione degli insiemi ottenuti con la formula di prima, nell’esempio precedente, se la loro chiusura determina tutto $R$ allora questa intersezione è l’unica chiave:

(A B D E \cap A C D E \cap A BC D)^{+} = (A D)^{+} = A D

Quindi avremmo potuto capire che esiste più di una chiave, infatti ce ne sono 2.

Una volta determinate le chiavi possiamo passare alla verifica di $3 NF$ per ognuna di queste, e quindi verificare che:

\forall X \to A \in F^{+}, A \neq \in X

$A$ è primo (fa parte di una chiave) Oppure
$X$ contiene una chiave

Decomposizione di Uno Schema

Se non siamo in $3 NF$ gli schemi vanno decomposti:

I sottoschemi devono essere in 3NF
Dobbiamo preservare le dipendenze in $F^{+}$
Il join dei sottoschemi devi farci ottenere istanze valide dello schema di partenza

Inoltre non sempre li decomponiamo per ottenere una 3NF ma anche per motivi di efficienza degli accessi.

Definizione Decomposizione Schema

Iniziamo a dare delle definizioni: Sia $R$ uno schema di relazione. Una Decomposizione di $R$ è una famiglia di $ρ = {R_{1}, R_{2}, \dots, R_{k}}$ di sottoinsiemi di $R$ che ricopre $R$ ( $⋃_{i = 1}^{k} R_{i} = R$ ), i sottoinsiemi possono avere intersezioni non vuota.

Quindi decomporre uno schema $R$ significa definire dei sottoschemi che contengono ognuno un insieme degli attributi di $R$ , questi possono avere attributi in comune e la loro unione deve necessariamente contenere tutti gli attributi di $R$ .

” $R$ è un insieme di attributi e una decomposizione di $R$ è una famiglia di insiemi di attributi”.

Quindi possiamo avere anche più decomposizioni ma poi dobbiamo verificare se sono “buone” ovvero se i sottoschemi preservano la 3NF, le dipendenze funzionali e facendo un join non abbiamo perdite.

Definizione Decomposizione Istanza

Decomporre un’istanza significa invece fare una proiezione dello schema originale con gli attributi del sottoschema, eliminando eventuali duplicati generati dal fatto che nello schema originale magari due tuple sono distinte ma considerando solo una parte degli attributi, ovvero il sottoschema, risultano uguali.

Esempio

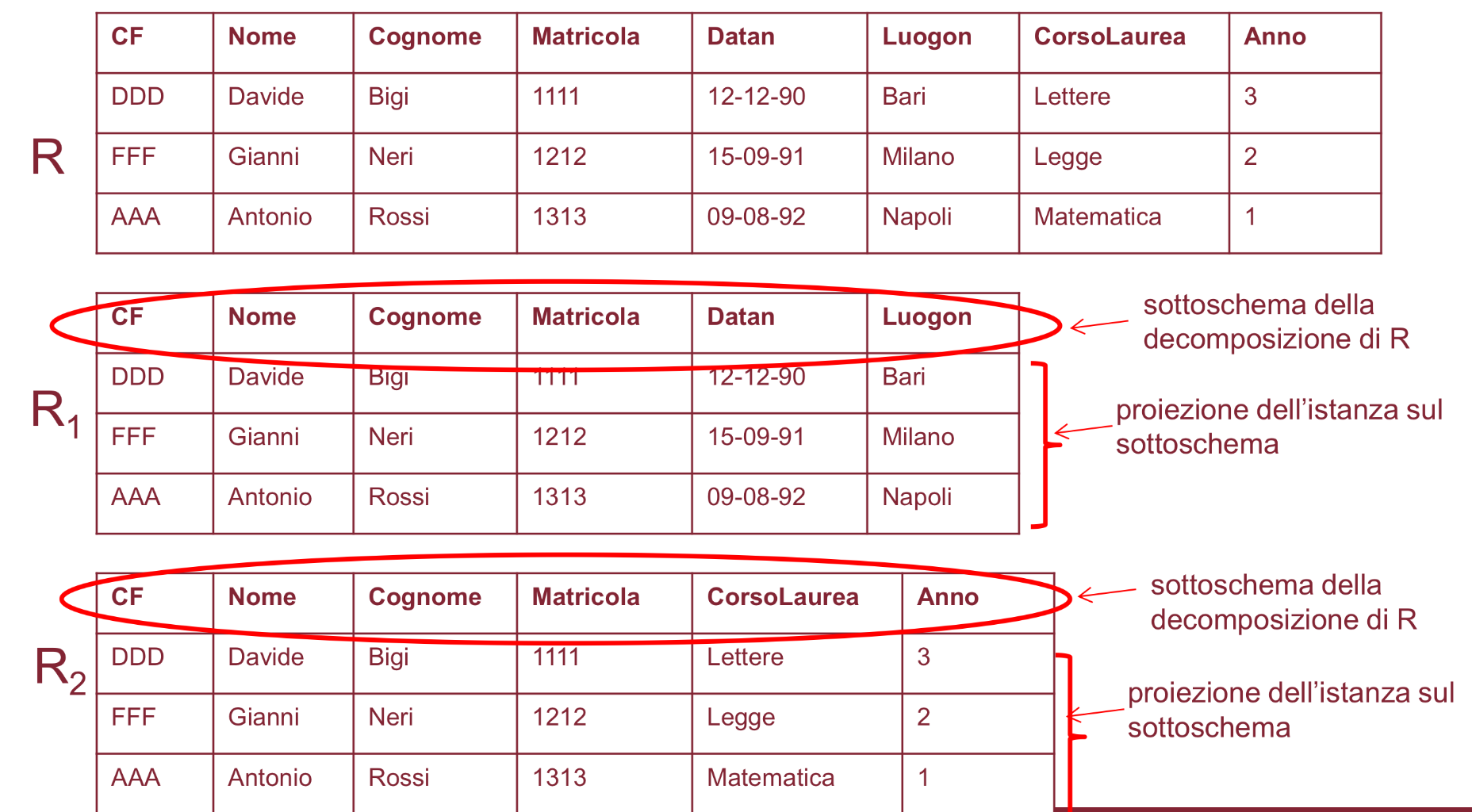
Definizione Equivalenza tra due insiemi di dipendenze funzionali

Siano $F$ e $G$ due insiemi di dipendenze funzionali, sono equivalenti $F \equiv G$ se $F^{+} = G^{+}$ , quindi $F$ , e $G$ non contengono le stesse dipendenze ma le loro chiusure si.

Verificare Equivalenza di due insiemi di Dipendenze Funzionali

Quindi per verificare l’equivalenza dobbiamo verificare l’uguaglianza tra le loro chiusure, ovvero $F^{+} \subseteq G^{+}$ e che $G^{+} \subseteq F^{+}$ .

Come visto prima calcolare la chiusura di un insieme di dipendenze richiede tempo esponenziale, ma questo lemma ci viene in aiuto.

Lemma 2

Siano $F$ e $G$ due insiemi di dipendenze funzionali, se $F \subseteq G^{+}$ allora $F^{+} \subseteq G^{+}$

Dimostrazione

Sia $f \in F^{+} - F$ , quindi è una dipendenza che sta in $F^{+}$ ma non in $F$ .
Ogni dipendenza che si trova in $F$ è derivabile da $G$ per gli assiomi di Armstrong, infatti per la nostra ipotesi $F \subseteq G^{+}$ e per il teorema $G^{+} = G^{A}$ . Infatti se $F \subseteq G^{+}$ significa che $F$ fa parte della chiusura di $G$ ed è quindi derivabile da $G$ mediante gli assiomi di Armstrong

G A F

Dato che $F^{+} = F^{A}$ abbiamo $f$ è derivata da $F$ tramite Armstrong.

F A F^{+}

E quindi $f$ è derivabile da $G$ mediante gli assiomi di Armstrong, infatti dato che $F$ sta in $G^{+}$ significa che abbiamo applicato Armstrong a tutto e quindi anche $F^{+}$ sta in $G^{+}$ .

G A F A F^{+}

Adesso possiamo dare la definizione.

Sia $R$ uno schema di relazione, $F$ un insieme di dipendenze funzionali su $R$ e $ρ = {R_{1}, \dots, R_{k}}$ una decomposizione di $R$ diciamo che $ρ$ preserva $F$ se:

F \equiv i = 1 ⋃ k π_{R i} (F)

Dove con $π_{R i} (F)$ indichiamo ${X \to Y t . c . X \to Y \in F^{+} \land X Y \subseteq R_{i}}$ quindi è l’insieme delle dipendenze funzionali che appartengono ad $F^{+}$ e sono “compatibili” con il sottoschema ovvero che gli attributi che compaiono nella relazione sono contenuti nel sottoschema.

In modo formale quindi $π_{R i} (F)$ è un insieme di dipendenze funzionali dato dalla proiezione dell’insieme di dipendenze funzionali $F$ sul sottoschema $R_{i}$ e proiettare un insieme di dipendenze $F$ su un sottoschema $R_{i}$ significa prendere tutte e sole le dipendenze in $F^{+}$ che hanno tutti gli attributi in $R_{i}$ .

Adesso supponiamo di avere già una decomposizione e di voler verificare se preserva le dipendenze funzionali.

Verificare se una decomposizione preserva un insieme di dipendenze $F$ richiede che venga verificata l’equivalenza dei due insiemi di dipendenze funzionali $F$ e $G = i = 1 ⋃ k π_{R i} (F)$ . Quindi dobbiamo verificare che $G^{+} \subseteq F^{+}$ e che $F^{+} \subseteq G^{+}$ .

Per come abbiamo definito $G$ sappiamo che i suoi elementi sono proiezioni di dipendenze di $F$ , inoltre sappiamo che $F^{+}$ contiene queste proiezioni (condizione dell’and) e quindi $F^{+}$ contiene $G$ , scritto più formalmente abbiamo che $G \subseteq F^{+}$ che per il lemma 2 implica che $G^{+} \subseteq F^{+}$ .

Quindi adesso ci manca da verificare che $F \subseteq G^{+}$ che poi con il lemma ci porta a dire che $F^{+} \subseteq G^{+}$ .

Questa verifica può essere fatta tramite un algoritmo. Algoritmo contenimento di F in $G^{+}$

Input: Due insiemi $F$ e $G$ di dipendenze funzionali su $R$
Output: Una variabile che indica true se $F \subseteq G^{+}$ , altrimenti false

begin successo := t r u e foreach (X \to Y \in F) : calcola X_{G}^{+} if (Y \neq \in X_{G}^{+}) : successo := f a l se end end

Infatti se $Y \neq \in X_{G}^{+}$ per il lemma abbiamo che $X \to Y \neq \in G^{A}$ e quindi neanche in $G^{+}$ per il teorema. Basta quindi trovare una sola dipendenza che non rispetta la condizione per poter affermare che non c’è equivalenza.

Ma come calcoliamo $X_{G}^{+}$ ? Infatti non possiamo utilizzare l’algoritmo che conosciamo dato che non sappiamo come è fatta $G$ , inoltre per la definizione di $G$ dobbiamo prima calcolare $F^{+}$ ma richiede tempo esponenziale.

Vediamo quindi un algoritmo che ci permette di calcolare $X_{G}^{+}$ a partire da $F$ .

Input: uno schema $R$ , un insieme $F$ di dipendenze funzionali su $R$ , una decomposizione $ρ = {R_{1}, \dots, R_{k}}$ di $R$ e un sottoinsieme $X$ di $R$ .
Output: La chiusura di $X$ rispetto a $G = i = 1 ⋃ k π_{R i} (F)$ , in questo caso lo inseriamo nella variabile $Z$ .

begin Z := X S := \emptyset for (i := 1, i \leq k, i + +) : S := S \cup (Z \cap R_{i})_{F}^{+} \cap R_{i} while (S \neq \subset Z) : Z := Z \cup S for (i := 1, i \leq k, i + +) : S := S \cup (Z \cap R_{i})_{F}^{+} \cap R_{i} end

Nel primo for stiamo raccogliendo gli attributi determinati da $Z$ ovvero il nostro $X$ , e grazie all’intersezione ci assicuriamo che sia dipendenti che dipendente si trovino nel sottoschema, tutti questi li raccogliamo in $S$ .

Poi con il while quello che andiamo a fare è essenzialmente raccogliere in $Z$ tutti gli attributi che sono determinati da $X$ anche se $X$ non si trova nel sottoschema, questo perché magari sono determinati da attributi presenti in altri schemi dove in questi sono determinati da $X$ .

Per fare questo utilizziamo le dipendenze nella chiusura di $F$ dato che sappiamo che le dipendenze che formano $G$ sono incluse in $F^{+}$ .

Ricordiamo che l’algoritmo per definizione termina sempre, ci fornisce la chiusura di un insieme di attributi rispetto ad un insieme di dipendenze funzionali che non conosciamo, ma sappiamo essere incluso in un altro, questo risultato dobbiamo quindi utilizzarlo insieme all’algoritmo visto precedentemente per l’equivalenza di due insiemi di dipendenze.

Teorema Dimostrazione Algoritmo

Sia $R$ uno schema di relazione, $F$ un insieme di dipendenze funzionali su $R$ e $ρ = {R_{1}, \dots, R_{k}}$ una decomposizione di $R$ . Prendiamo $X$ un sottoinsieme di $R$ . L’algoritmo calcola correttamente $X_{G}^{+}$ dove $G = ⋃_{i = i}^{k} π_{R i} (F)$ .

Dimostrazione

Dato che l’algoritmo aggiunge sempre qualcosa alla chiusura senza mai togliere nulla, possiamo procedere per induzione.

Indichiamo con $Z^{0}$ il valore iniziale di $Z$ e con $Z^{i}$ il valore di $Z$ dopo l’i-esima esecuzione dell’assegnazione $Z = Z \cup S$ , è facile vedere che $Z^{i} \subseteq Z^{i + 1}$ per ogni i.

Sia $Z^{f}$ il valore di $Z$ quando l’algoritmo termina, proveremo che:

A \in Z^{f} \Leftrightarrow A \in X^{+} G

Parte solo se

Mostriamo che $Z^{i} \subseteq X_{G}^{+}$ per ogni $i$ , in particolare per $f = i$

Base dell’induzione $i = 0$ , poiché $Z^{0} = X$ e $X \subseteq X^{+}$ si ha che $Z^{0} \subseteq X_{G}^{+}$ .
Induzione: $i > 0$ , per ipotesi induttiva abbiamo che $Z^{i - 1} \subseteq X_{G}^{+}$ , con $i$ indichiamo le iterazione del while

Sia $A$ un attributo in $Z^{i} - Z^{i - 1}$ ovvero che lo abbiamo aggiunto nell’iterazione appena fatta, significa che quindi esiste un indice $j$ della decomposizione tale che $A \in (Z^{i - 1} \cap R_{j})_{F}^{+} \cap R_{j}$ .

Poiché $A \in (Z^{i - 1} \cap R_{j})_{F}^{+}$ possiamo dire che $(Z^{i - 1} \cap R_{j}) \to A \in F^{+}$ .

Quindi sappiamo che:

$(Z^{i - 1} \cap R_{j}) \to A \in F^{+}$
$A \in R_{j}$ (appartiene all’intersezione fra la chiusura e $R_{j}$ vista prima)
$Z^{i - 1} \cap R_{j} \subseteq R_{j}$

Adesso per la definizione di $G$ si ha che $Z^{i - 1} \cap R_{j} \to A \in G$ , infatti in $G$ abbiamo le proiezione delle dipendenze sui sottoschemi e siccome abbiamo l’intersezione con $R_{j}$ sappiamo che si trova in un sottoschema.

Per ipotesi induttiva sappiamo che $Z^{i - 1} \subseteq X_{G}^{+}$ ovvero che $X \to Z^{i - 1} \in G^{+}$ e per la regola della decomposizione possiamo dire che $X \to Z^{i - 1} \cap R_{j} \in G^{+}$ .

Possiamo quindi usare l’assioma della transitività, dato che $X \to Z^{i - 1} \cap R_{j} \in G^{+}$ e che $Z^{i - 1} \cap R_{j} \to A \in G$ possiamo dire che $X \to A \in G^{+}$ e quindi che $A \in X_{G}^{+}$ . Quindi $Z^{i} \subseteq X_{G}^{+}$ .

Abbiamo mostrato che vengono inseriti anche gli elementi della i-esima iterazione mentre quelli delle precedenti ci sono per ipotesi.

Parte Se non ci interessa

Join Senza Perdita

Quando uno schema viene decomposto abbiamo visto che non basta mantenere la 3NF sui sottoschemi, dobbiamo anche mantenere tutte le dipendenze e tutti i dati dell’istanza originale quando effettuiamo un join sui sottoschemi, per perdita di dati intendiamo in realtà un’aggiunta di informazioni estranee allo schema originale. (Fatti esempi più sopra).

Quindi quando decomponiamo uno schema abbiamo come obiettivo: permettere la ricostruzione di ogni istanza legale dello schema originale mediante join naturale.

Definizione

Sia $R$ uno schema di relazione, una decomposizione $ρ = {R_{1}, \dots, R_{k}}$ di $R$ ha un join senza perdita se per ogni istanza legale $r$ di $R$ si ha che:

r = π_{R_{1}} (r) ⋈ \dots ⋈ π_{R_{k}} (r)

Infatti facendo la proiezione di un’istanza su ogni sottoschema otteniamo “una parte” di quell’istanza, facendo il join dobbiamo ricomporla tutta.

Partiamo da una decomposizione data e cerchiamo un modo per verificare che soddisfi la proprietà data.

Teorema

Sia $R$ uno schema di relazione e $ρ = {R_{1}, \dots, R_{k}}$ una decomposizione di $R$ . Per ogni istanza legale $r$ di $R$ , indicato con $m_{ρ} (r) = π_{R_{1}} (r) ⋈ \dots ⋈ π_{R_{k}} (r)$ si ha che:

$r \subseteq m_{ρ} (r)$
$π_{R i} (m_{ρ} (r)) = π_{R i} (r)$
$m_{ρ} (m_{ρ} (r)) = m_{ρ} (r)$

Abbiamo uno schema $R$ e un insieme di dipendenze funzionali $F$ e una decomposizione $ρ$ , come verifichiamo che la decomposizione ha un join senza perdita? Possiamo farlo tramite un algoritmo di verifica che agisce in tempo polinomiale ovvero $O (n^{k})$ per una qualche costante $k$ .

Input: uno schema di relazione $R$ , un insieme $F$ di dipendenze funzionali su $R$ e una decomposizione $ρ = {R_{1}, \dots, R_{k}}$ di $R$ .
Output: un booleano che ci dice se $ρ$ ha un join senza perdita.

Costruiamo una tabella $r$ in modo tale da avere un numero di colonne pari al numero degli attributi di $R$ e un numero di righe pari al numero di sottoschemi presenti nella decomposizione $ρ$ .

Nelle celle che si incontrano all’indice $i$ per le righe e $j$ per le colonne inseriamo il simbolo $a_{j}$ se l’attributo $A_{j} \in R_{i}$ ovvero se l’attributo della colonna $j$ appartiene al sottoschema della riga $i$ . Altrimenti inseriamo $b_{ij}$ .

Adesso per ogni dipendenza $X \to Y \in F$ controlliamo se nella tabella ci sono tuple che non rispettano la dipendenza ovvero tali che $t_{1} [X] = t_{2} [X]$ e $t_{1} [Y] \neq = t_{2} [Y]$ , e a questo punto le facciamo diventare “legali”, se in una tupla è presente una $a$ nell’attributo $Y$ allora propaghiamo questa $a$ a tutte le altre, altrimenti scegliamo un $b$ a piacere e la propaghiamo su tutte le altre.

Se abbiamo apportato modifiche continuiamo ad applicare l’algoritmo altrimenti ci fermiamo. Ci fermiamo anche se in una riga ci sono tutte $a$ .

Se quando ci fermiamo è presente una riga con tutte $a$ allora la decomposizione ha join senza perdita.

Osservazione

Possiamo considerare gli $a_{j}$ come valori particolari appartenenti al dominio dell’attributi $A_{j}$ .

Possiamo considerare i $b_{ij}$ come valori particolari appartenenti al dominio dell’attributo $A_{j}$

Possiamo considerare tutti i valori $a_{j}$ uguali tra di loro

Il valore $b_{ij}$ è diverso da $a_{j}$ e da un altro valore $b_{kj}$ anche se appartengono tutti allo stesso dominio dell’attributo $A_{j}$

Quindi la nostra $r$ iniziale è una particolare istanza dello schema $R$ che trasformiamo in un’istanza legale e per fare questo dobbiamo fare in modo che tutte le dipendenze in $F$ siano soddisfatte.

Infatti quando troviamo tuple uguali sugli attributi di sinistra (determinanti) allora facciamo in modo che siano uguali anche sui dipendenti, dando precedenza alle $a$ .

Quando ci fermiamo significa che abbiamo costruito un’istanza legale di $R$

Esempio

Dato lo schema $R = {A, B, C, D, E}$ e $F = {C \to D, A B \to E, D \to B}$ , dire se la decomposizione $ρ = {A C, A D E, C D E, A D, B}$ ha un join senza perdita.

Costruiamo la tabella

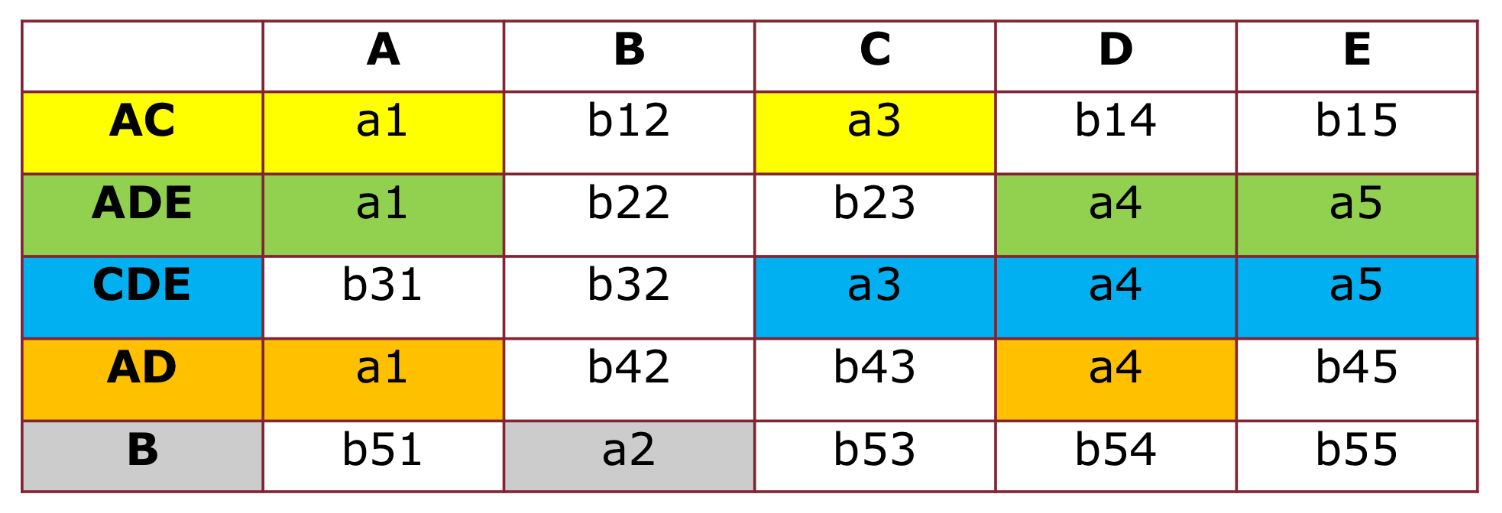
Adesso iniziamo a verificare le dipendenze:

$C \to D$ , prima e terza riga sono uguali su C ma diverse su D, sulla riga 3 abbiamo $a_{4}$ quindi la portiamo anche alla prima riga
$A B \to E$ è già soddisfatta
$D \to B$ , abbiamo 3 tuple uguali su D e diverse su B, non abbiamo nessuna $a$ quindi scegliamo una $b$ e la portiamo su tutte le righe

Scriviamo la tabella e siccome abbiamo effettuato modifiche e non abbiamo $a$ su un’intera riga, continuiamo ad applicare l’algoritmo.

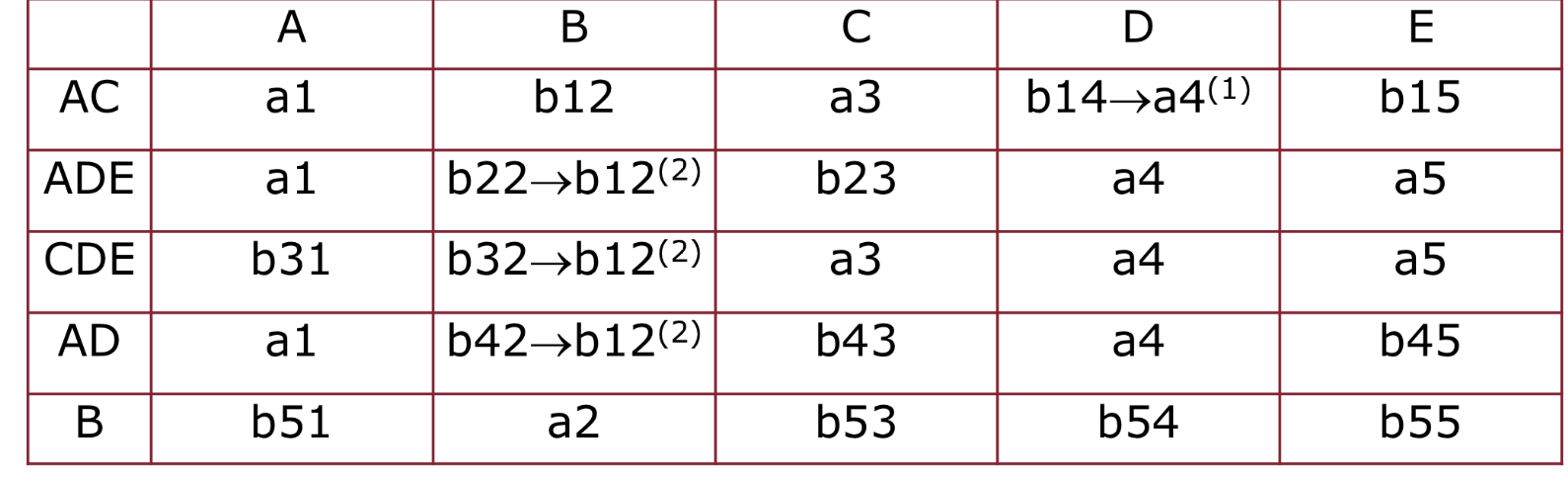
$C \to D$ è già soddisfatta
$A B \to E$ abbiamo 3 tuple uguali su AB e diverse su E, sulla E abbiamo $a_{5}$ quindi portiamo $a_{5}$ su tutte le tuple
$D \to B$ già soddisfatta

Scriviamo la tabella e continuiamo con le iterazioni

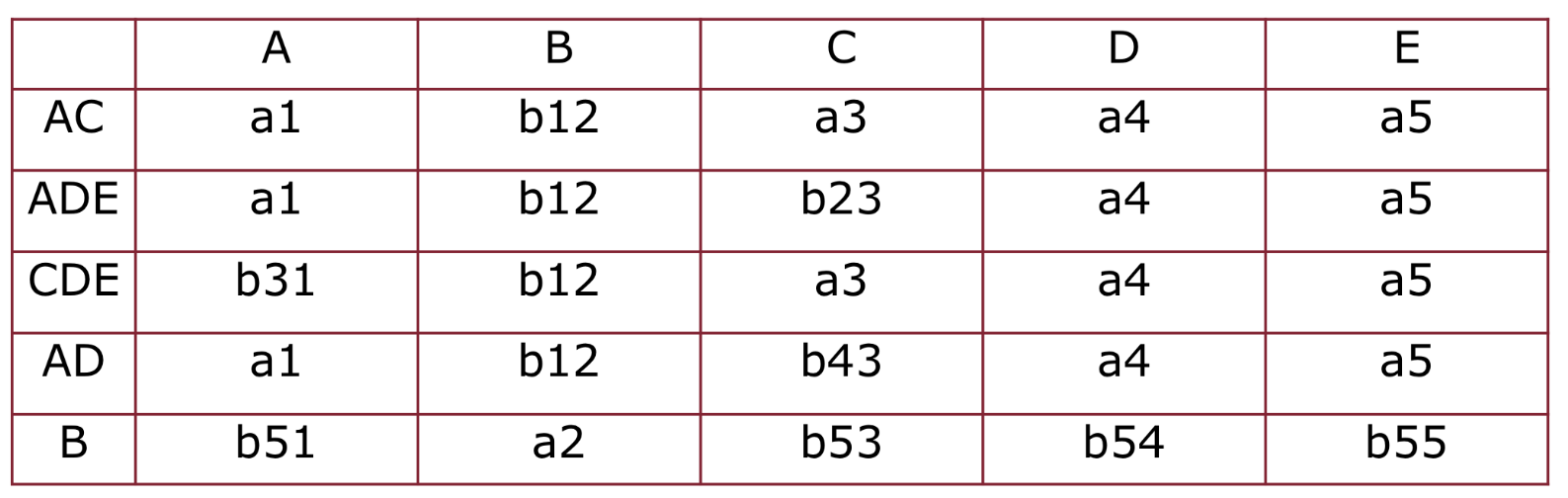
Adesso notiamo che tutte e 3 le dipendenze sono soddisfatte e quindi non facciamo cambiamenti in questa iterazione, l’algoritmo si ferma.

Abbiamo una riga con tutte $a$ ? No quindi la decomposizione non ha join senza perdita.

Non so se serve la dimostrazione di questo algoritmo di verifica (spoiler serviva)

Ottenere una decomposizione con Join senza perdita

Abbiamo visto sempre come verificare che una decomposizione non abbia perdita nel join, ma è sempre possibile ottenere una decomposizione con questa proprietà? Si, è possibile tramite un algoritmo.

Ci sono alcune osservazioni da fare, la decomposizione che si ottiene da questo algoritmo non è l’unica possibile, quindi se ci viene fornito uno schema e una decomposizione ma con l’algoritmo non ci viene restituita la stessa non significa che una delle due è sbagliata, potrebbero essere entrambe corrette. È importante quindi utilizzare i due algoritmo nel momento giusto, uno per la verifica e uno per ottenere decomposizioni.

Per usare questo algoritmo ci serve il concetto di copertura minimale di un insieme di dipendenze. Questa copertura è l’input dell’algoritmo e ce dato un insieme di dipendenze ci possono essere più coperture minimali, proprio per questo l’algoritmo può fornire diverse decomposizioni.

Copertura Minimale

Sia $F$ un insieme di dipendenze funzionali, una copertura minimale di $F$ è un insieme $G$ equivalente ad $F$ tale che:

Ogni dipendenza funzionale di $G$ ha la parte destra che è un singleton.
Per nessuna dipendenza funzionale $X \to A \in G$ esiste $X^{'} \subset X$ tale che $G \equiv G - {X - A} \cup {X^{'} \to A}$ ovvero gli attributi nella parte sinistra non sono ridondanti. Ad esempio se abbiamo $A B \to C$ non dobbiamo avere $A \to C$ e $B \to C$ .

Non deve essere quindi possibile determinare $A$ tramite un sottoinsieme di $X$ .
Per nessuna dipendenza funzionale $X \to A \in G$ deve accadere $G \equiv G - {X \to A}$ , ovvero ogni dipendenza è non ridondante. Ad esempio se abbiamo $A \to C$ $A \to B$ e $B \to C$ possiamo eliminare $A \to C$ dato che possiamo ricostruirla per transitività.

Non deve essere possibile determinare $A$ tramite altre dipendenze.

Vediamo come calcolare questa copertura minimale.

Per ogni insieme $F$ di dipendenze funzionali esiste una copertura minimale equivalente ottenibile in tempo polinomiale.

Passaggi:

Usando la regola della decomposizione riduciamo i dipendenti in singleton
Per ogni dipendenza funzionale $A_{1}, \dots, A_{i - 1}, A_{i}, A_{i + 1}, \dots A_{n} \to A \in F$ tale che $F \equiv F - {A_{1}, \dots, A_{i - 1}, A_{i}, A_{i + 1}, \dots A_{n} \to A \in F} \cup {A_{1}, \dots, A_{i - 1}, A_{i + 1}, \dots A_{n} \to A \in F}$ questa viene sostituita appunto da $A_{1}, \dots, A_{i - 1}, A_{i + 1}, \dots A_{n} \to A \in F$ ovvero la dipendenza che ha come determinante il sottoinsieme del precedente determinante. Se invece questa dipendenza è già presente allora eliminiamo semplicemente quella più grande. Applichiamo ricorsivamente il passo finché non è più possibile ridurre dipendenze.
Ogni dipendenza $X \to A \in F$ tale che $F \equiv F - {X \to A}$ viene eliminata dato che è ridondante.

I passi 2 e 3 ovviamente richiedono una verifica dell’equivalenza, ma ci troviamo in dei casi particolari.

Per il passo 2 assumiamo che $F$ sia l’insieme che contiene la dipendenza originaria e con $G$ l’insieme che contiene quella “ridotta”. Notiamo che i due insieme differiscono soltanto di una dipendenza, quindi tutte le altre sono uguali e appartengono quindi alle loro chiusure. Per verificare quindi l’equivalenza dobbiamo solo verificare che la dipendenza originale si trova in $G^{+}$ e quella ridotta si trova in $F^{+}$ .

Per calcolare le chiusure degli insiemi usiamo l’algoritmo, che a sua volta calcola le chiusure degli insiemi di attributi. Andare a verificare se la dipendenza originale si trova in $G^{+}$ è superfluo dato che in $G^{+}$ abbiamo quella con un dipendente in meno, e quindi se aggiungiamo qualcosa non cambia nulla.

Banalmente, se abbiamo $A \to C$ sarà vero anche $A B \to C$ .

Esempio

Abbiamo $F = {A B \to C, A \to D, D \to C}$ , per verificare se possiamo eliminare la $B$ in $A B \to C$ dobbiamo verificare se $A \to C \in F^{+}$ e se $A B \to C \in G^{+}$ . Per la prima ci basta applicare l’algoritmo e notiamo che $C \in A_{F}^{+}$ mentre per la seconda è banale dato che $G = {A \to D, A \to C, D \to C}$ infatti compare $A \to C$ .

Adesso ci manca da verificare che $X^{'} \to A \in F^{+}$ e per farlo usiamo l’algoritmo per verificare se $A \in X_{F}^{+}$ , dobbiamo quindi calcolarlo. Se questo accade possiamo ridurre la dipendenza o rimuoverla in alcuni casi.

Passo 3

Assumiamo di chiamare $F$ l’insieme che contiene $X \to A$ e con $G$ l’insieme dove è stata eliminata. Anche in questo caso i due insiemi differiscono di una sola dipendenza e inoltre si verifica che $G \subseteq F$ e quindi già sappiamo $G^{+} \subseteq F^{+}$ . Ci manca quindi da verificare che $F^{+} \subseteq G^{+}$ che sarà vero se $F \subseteq G^{+}$ .

In particolare ci basta verificare che $X \to A \in G^{+}$ ovvero $A \in X_{G}^{+}$ .

Riassumendo

Indichiamo con $F$ l’insieme che contiene la dipendenza $X \to A$ e con $G$ quello che contiene al suo posto $X^{'} \to A$ dove $X^{'} \subset X$ . Per il passo 2:

Dobbiamo verificare che $A \in X_{F}^{' +}$ , se accade riduciamo la dipendenza, o se presenti entrambe in $F$ eliminiamo $X \to A$ .
Se $X \to A \in F$ e $Y \to A \in F$ tale che $Y \subseteq X$ allora eliminiamo $X \to A \in F$ .
Se $X \to A \in F$ ma non esiste $Y \to A \in F$ con $Y \neq = X$ allora è inutile provare ad eliminare attributi a sinistra della dipendenza.
È inutile ricalcolare chiusure transitive di attributi o di gruppi di attributi.

Per il passo 3, assumiamo $F$ che contiene l’originale $X \to A$ e $G$ che non la contiene. Dobbiamo verificare $F \equiv G$ e per farlo ci basta verificare $X \to A \in G^{+}$ ovvero se $A \in X_{G}^{+}$ :

Se $X \to A \in F$ ma non esiste $Y \to A \in F$ con $F \neq = X$ allora è inutile provare ad eliminare $X \to A$ .
Vanno ricalcolate le chiusure di attributi e gruppi di attributi.

Esempio

Algoritmo di Decomposizione

Dato uno schema di relazione $R$ e un insieme di dipendenze funzionali $F$ su $R$ esiste sempre una decomposizione $ρ = {R_{1}, \dots, R_{k}}$ di $R$ tale che:

Per ogni $i = 1, \dots, k$ abbiamo $R_{i}$ in 3NF
$ρ$ preserva $F$
$ρ$ ha un join senza perdita

Inoltre tale decomposizione può essere calcolata in tempo polinomiale.

L’algoritmo prende come $F$ una copertura minimale, ci va bene una qualsiasi.

Algoritmo

S := \emptyset for every A \in R tale che A non \overset{e}{ˋ} coinvolto in nessuna dipendenza funzionale in F S := S \cup {A} if S \neq = \emptyset then R := R - S ρ := ρ \cup {S} if esiste una dipendenza funzionale in F che coinvolge tutti gli attributi in R ρ := ρ \cup {R} else for every X \to A ρ := ρ \cup {X A}

Dimostrazione Algoritmo

Abbiamo detto che l’algoritmo permette di calcolare una decomposizione che in tempo polinomiale ha ogni sottoschema in 3NF e preserva le dipendenze.

Dimostriamo le due proprietà.

$ρ$ preserva $F$ .

Sia $G = ⋃_{i = 1}^{k} π_{R i} (F)$ . Poiché per ogni dipendenza funzionale $X \to A \in F$ si ha che $X A \in ρ$ (dato che è un sottoschema, li aggiungiamo in un passo dell’algoritmo) e quindi questa dipendenza di $F$ sarà sicuramente in $G$ , quindi dato che $F \subseteq G$ allora $F^{+} \subseteq G^{+}$ , l’inclusione inversa è verificata dato che per definizione abbiamo che $G \subseteq F^{+}$ .

Ogni schema di relazione in $ρ$ è in 3NF

Si possono verificare diversi casi:

Se $S \in ρ$ ogni attributo in $S$ fa parte della chiave e quindi banalmente $S$ è in 3NF (infatti in S abbiamo gli attributi che non compaiono nelle dipendenze, questo significa che non vengono mai determinati e quindi si trovano sicuramente nella chiave)
Se $R \in ρ$ esiste una dipendenza funzionale che coinvolge tutti gli attributi, siccome $F$ è una copertura minimale, avrà forma $R - A \to A$ inoltre non ci possono essere dipendenze $X \to A$ in $F$ tali che $X \subset R - A$ e quindi $R - A$ è chiave in $R$ (coinvolge tutti gli attributi). Inoltre sia $B$ una qualsiasi dipendenza in $F$ , se $B = A$ allora, siccome $F$ minimale, $Y = R - A$ ovvero $Y$ superchiave e quindi mantiene la 3NF. Se invece $B \neq = A$ allora $B \in R - A$ che è chiave e quindi $B$ è primo, rispetta ancora la 3NF.
Se $X A \in ρ$ , dato che $F$ è una copertura minimale, non ci può essere dipendenza funzionale $X^{'} \to A \in F$ tale che $X^{'} \subset X$ e quindi $X$ è chiave in $X A$ . Inoltre sia $Y \to B$ una qualsiasi dipendenza in $F$ tale che $Y B \subseteq X A$ se $B = A$ allora poiché $F$ è una copertura minimale $Y = X$ ovvero $Y$ superchiave e quindi rispettiamo la 3NF, se invece $B \neq = A$ allora $B$ deve essere in $X$ che è chiave e quindi $B$ è primo, rispettiamo ancora la 3NF.

Come facciamo ad ottenere un join senza perdita?

Ci basta aggiungere un sottoschema contenente una chiave al risultato dell’algoritmo di decomposizione. Adesso però dobbiamo dimostare che questa aggiunta non ci fa perdere gli obiettivi ottenuti prima.

Teorema

Sia $R$ uno schema di relazione e $F$ un insieme di dipendenze funzionali su $R$ , che è una copertura minimale, inoltre sia $ρ$ la decomposizione di $R$ prodotta dall’algoritmo di decomposizione. La decomposizione $σ = ρ \cup {K}$ dove $K$ è una chiave per $R$ , è tale che:

Ogni schema di $σ$ è 3NF
$σ$ preserva $F$
$σ$ ha un join senza perdita

IN TEORIA NON LE CHIEDE

Dimostrazione

$σ$ preserva $F$ , infatti dato che $ρ$ preserva $F$ , lo farà anche $σ$ .

Infatti stiamo aggiungendo un nuovo sottoschema, una nuova proiezione di $F$ . Chiamiamo $G^{'}$ il nuovo $G$ , e lo definiamo come $G^{'} = G \cup π_{K} (F)$ quindi $F \subseteq G \subseteq G^{'}$ e quindi $F^{+} \subseteq G^{+} \subseteq G^{' +}$ . L’inclusione inversa è banalmente verificata per lo stesso motivo del teorema precedente.

Ogni schema di relazione in $σ$ è in 3NF

Poiché $σ = ρ \cup {K}$ , è sufficiente verificare che anche lo schema $K$ sia in 3NF, dobbiamo mostrare che $K$ è chiave anche per lo schema $K$ .

Supponiamo per assurdo che non lo sia, allora esiste un sottoinsieme proprio $K^{'}$ di $K$ che determina tutto lo schema $K$ ovvero tale che $K^{'} \to K \in F^{+}$ o più precisamente appartiene alla chiusura $π_{K} (F)$ ma questa è sottoinsieme di $F^{+}$ . Poiché $K$ è chiave per lo schema $R$ , ovvero $K \to R \in F^{+}$ , per transitività si ha che $K^{'} \to R \in F^{+}$ che contraddice il fatto che $K$ è chiave per lo schema $R$ . Quindi $K$ è chiave per lo schema $K$ e per ogni dipendenza funzionale $X \to A \in F^{+}$ con $X A \subseteq K$ , $A$ primo.

$σ$ ha un join senza perdita

Continuare dimostrazione, slide 19 con aggiunte pag. 13

Supponiamo che l’ordine in cui gli attributi in $R - K$ vengono aggiunti a $Z$ dell’algoritmo che calcola la chiusura di un insieme di attributi (qui $K^{+}$ ) sia $A_{1}, \dots, A_{n}$ e supponiamo che per ogni $i = 1, \dots, n$ l’attributo $A_{i}$ venga aggiunto a $Z$ a causa della presenza

SPERO NON LE CHIEDA VERAMENTE 🥶

Quindi presa un qualsiasi schema di DB possiamo farlo diventare “buono” effettuando decomposizioni per portarlo in 3NF.

👨🏻‍💻 Alem's Notes

BD1 - Prima e Seconda Parte

Modello dei dati

Modello Relazionale

Livelli di Astrazione di un DB

Indipendenza dei Dati

Schemi e Istanze

Linguaggi per le Basi di Dati

Ricapitolando

Integrità

Sicurezza

Concorrenza

Modello Relazionale

Definizioni

Relazioni e Tabelle

Valori

Vincoli

Vincoli Intra-Relazionali

Vincoli Inter-Relazionali

Chiavi

Vincolo di Integrità Referenziale

Dipendenze Funzionali

Algebra Relazionale

Proiezione

Selezione

Unione

Differenza

Intersezione

Algebra Relazionale II

Prodotto Cartesiano

Join Naturale

θ Join

Condizione Negative

Quantificatore Universale

Condizioni che richiedono il prodotto di una relazione con se stessa

Progettazione basi di dati - Problemi e Vincoli

Ipotesi 1

Ipotesi 2

Vincoli

Dipendenze Funzionali

Schema di relazione

Tupla

Istanza di Relazione

Chiusura di un insieme di Dipendenze Funzionali

Chiave

Chiave Primaria

Dipendenze Funzionali Banali

Proprietà delle dipendenze funzionali

Assiomi di Armstrong

Chiusura di un insieme di attributi

Terza Forma Normale

Dipendenze Parziali e Transitive

Dipendenze Parziali

Dipendenze Transitive

Definizione Alternativa 3NF

Definizioni a Confronto

Formale Normale di Boyce-Codd

Chiusura di un Insieme di Attributi

Calcolo di X+

Identificare le chiavi di uno Schema

Decomposizione di Uno Schema

Verificare Equivalenza di due insiemi di Dipendenze Funzionali

Join Senza Perdita

Ottenere una decomposizione con Join senza perdita

Copertura Minimale

Algoritmo di Decomposizione

Table of Contents

Backlinks

$θ$ Join

Calcolo di $X^{+}$