BD1 - Organizzazione Fisica

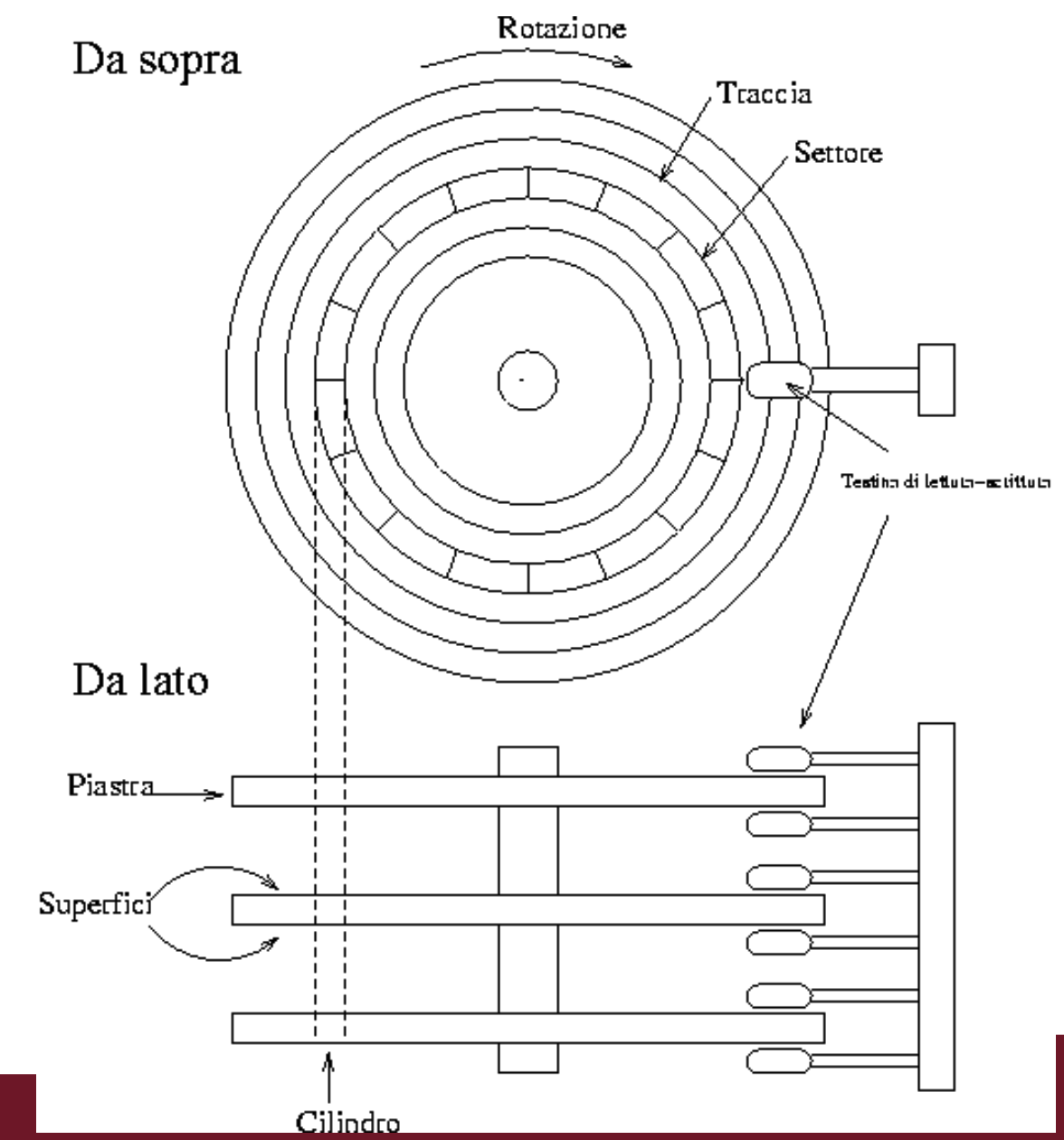
Questo è come si presenta un Hard Disk all’interno, a noi non interessa il tempo in cui il disco reperisce le informazioni ma il bensì il numero di accessi in memoria. Il trasferimento avviene sottoforma di blocchi di byte utilizzando dei buffer grandi quanto un blocco.

Il blocco di byte è la nostra unità di misura per lo spazio e per i trasferimenti.

Un file nel nostro caso è la struttura di memorizzazione di una tabella, questo può richiedere più blocchi per essere memorizzato e un blocco può essere allocato in memoria solo per intero, inoltre un record non può trovarsi “a cavallo” su più blocchi.

• Al momento della formattazione del disco, ogni traccia è suddivisa in blocchi di dimensione fissa.
• Per accesso intendiamo il trasferimento di un blocco da memoria secondaria a principale (lettura) o da memoria principale a secondaria (scrittura).

Quindi il tempo di trasferimento è dato da:

• Tempo di posizionamento della testina
• Ritardo di rotazione del disco, serve a posizionare le testina all’inizio del blocco
• Tempo di trasferimento dei dati

Definiamo il costo in numero di accessi, perché prendere un dato in memoria secondaria richiede molto più tempo dell’elaborazione in memoria principale.

Come indichiamo gli schemi che conosciamo?

• Ad ogni relazione corrisponde un file di record, tutti dello stesso tipo.
• Ad ogni attributo corrisponde un campo
• Ad ogni tupla corrisponde un record

Record

Da notare che in un record, oltre ai dati della tupla, possono esserci altri campi che contengono informazioni sul record stesso o puntatore ad altri record / blocchi.

Per poter accedere ad un campo di un record è necessario sapere qual è il primo byte del campo nel record, se tutti i campi hanno la stessa lunghezza ci basta ordinarli e in questo modo l’inizio di ciascun campo sarà sempre ad un numero fisso di byte dall’inizio del record, questo numeri di byte si chiama offset.

Se invece il record ha campi a lunghezza variabile allora l’offset potrebbe variare da record a record, possiamo utilizzare due strategie:

• all’inizio di ogni campo inseriamo un contatore che indica la lunghezza del campo in numero di byte
• All’inizio del record ci sono due puntatori (con puntatore intendiamo l’offset del campo) all’inizio di ciascun campo a lunghezza variabile, quest’ultimi sono sempre preceduti da tutti quelli a lunghezza fissa.

(Infatti ad esempio prendiamo due record di una tabella studente, due studenti avranno nome e cognome di lunghezza diversa fra loro, in alcuni casi.)

Con la prima strategia abbiamo dei tempi più grandi, dato che per trovare un campo dobbiamo scorrere tutti i precedenti.

Puntatori

I puntatori sono dei dati che ci permettono di accedere rapidamente al record / blocco, possono contenere:

• L’indirizzo del primo byte del record / blocco sul disco Oppure
• Nel caso di un record, una coppia (b,k) dove:
  • b è l’indirizzo del blocco che contiene il record
  • k è il valore della chiave

Utilizzando la seconda strategia possiamo muovere il record all’interno del blocco, dato che una volta identificato quest’ultimo andiamo a cercare la chiave. Se invece spostassimo all’interno del blocco un record utilizzando il primo tipo di puntatori avremo dei dangling pointer ovvero dei puntatori che puntano al niente, inutili.

Blocchi

Come per i record, anche i blocchi possono avere dello spazio per memorizzare dati aggiuntivi su di loro o puntatori ad altri blocchi.

Se un blocco contiene solo record di lunghezza fissa:

• Il blocco è suddiviso in aree (sottoblocchi) di lunghezza fissa ciascuna delle quali riesce a contenere un record.
• Dei bit di utilizzo all’inizio del blocco

Se si deve inserire un record nel blocco occorre cercare un’area non usata e quindi se il bit di utilizzo si trova in ciascun record potrebbe richiedere la scansione di tutto il blocco, per questo li raccogliamo tutti all’inizio.

Se invece il blocco ha record di lunghezza variabile:

• Si pone in ogni record un campo che ne specifica la lunghezza in byte Oppure
• Si pone all’inizio del blocco una directory con i puntatori ai record del blocco

Directory del blocco

È possibile realizzarla in diversi modi:

• Preceduta da un campo che specifica quanti sono i puntatori nella directory
• Una lista di puntatori (la fine si indica con uno 0)
• Ha dimensione fissa e contiene il valore 0 negli spazi che non contengono puntatori

Operazioni sulla base di dati

Un’operazione sulla base di dati consiste di:

• Ricerca
• Inserimento (implica ricerca se vogliamo evitare duplicati)
• Cancellazione (implica ricerca)
• Modifica (implica ricerca)

Tutte queste operazioni avvengono per i record. Notiamo infine che la ricerca è quindi alla base di tutte le altre operazioni.

Vogliamo che il nostro DBMS esegua queste operazioni in modo efficiente, ovvero il più rapidamente possibile.

Una particolare organizzazione fisica dei dati può rendere più efficienti alcune operazioni, quando si fa il progetto della base è quindi buona norma tenere presente quali saranno le operazioni eseguite più frequentemente.

In generale ad ogni oggetto base di un modello logico (schemi di relazione) corrisponde un file di record che hanno tutti lo stesso formato ovvero gli stessi campi.

Noi ci occuperemo di organizzazioni che consentono la ricerca di record in base al valore di uno o più campi chiave. Da notare che un valore della chiave non necessariamente identifica univocamente un record nel file, come invece accade nella teoria relazionale.

File Heap

Questa è una NON organizzazione, infatti i record vengono allocati in un ordine determinato soltanto dall’ordine di inserimento, questo porta a prestazioni peggiori in termini di ricerca e quindi di accessi in memoria ma se ammettiamo duplicati, l’inserimento è molto veloce, infatti non controllando se il file già esiste ci basta inserirlo alla fine.

In un file heap infatti un record viene sempre inserito come ultimo record del file e quindi tutti i blocchi ad eccezione dell’ultimo sono pieni. L’accesso al file avviene attraverso la directory che contiene i puntatori ai blocchi.

Ricerca

Se vogliamo cercare un record specifico dobbiamo cercare in tutto il file, iniziando dal primo record fino ad incontrare quello desiderato, quindi il tempo di ricerca varia in base a dove si trova il record. Se il record che cerchiamo si trova nell’i-esimo blocco avremo i accessi in memoria e quindi ha senso valutare il costo medio di ricerca.

Esempio Pratico

Abbiamo:

• $N=151$ record
• Ogni record ha 30 byte
• Ogni blocco contiene 65 byte
• Ogni blocco ha un puntatore di 4 byte al prossimo blocco

Quanti record interi possiamo inserire in ogni blocco? Dobbiamo eseguire:

$$\frac{65-4}{30}$$

Ovvero $65-4$ perché è la dimensione del blocco meno la dimensione del puntatore, poi dividiamo per 30 che è la dimensione di un record.

Otteniamo $2.03$ come risultato, ovviamente in un blocco non possiamo inserire dei record “a cavallo” e quindi prendiamo la parte intera inferiore, questo significa che in un blocco possiamo inserire 2 record. Quel $0.03$ di blocco non possiamo memorizzarlo in un nuovo blocco.

Quanti blocchi servono per memorizzare $N$ record? Calcoliamo:

$$\frac{N}{\text{Record per blocco}}=\frac{151}{2}=75.5$$

In questo caso dato che stiamo considerando i blocchi necessari per memorizzare un record, non arrotondiamo con la parte inferiore ma bensì con la superiore, quindi per memorizzare 151 record con i dati visti prima abbiamo bisogno di 76 blocchi.

Quindi quando effettuiamo una ricerca dobbiamo scorrere una lista di 76 blocchi, se abbiamo fortuna troviamo subito il blocco, ma potrebbe anche trovarsi in ultima posizione.

Abbiamo una situazione simile, Effettuiamo una ricerca quando la chiave ha valore che non ammette duplicato:

Definiamo con:

• $R$ il numero di record che possono trovarsi in un blocco, nell’esempio di prima sono 2.
• $N$ il numero di record
• $n=\frac{N}{R}$ il numero di blocchi

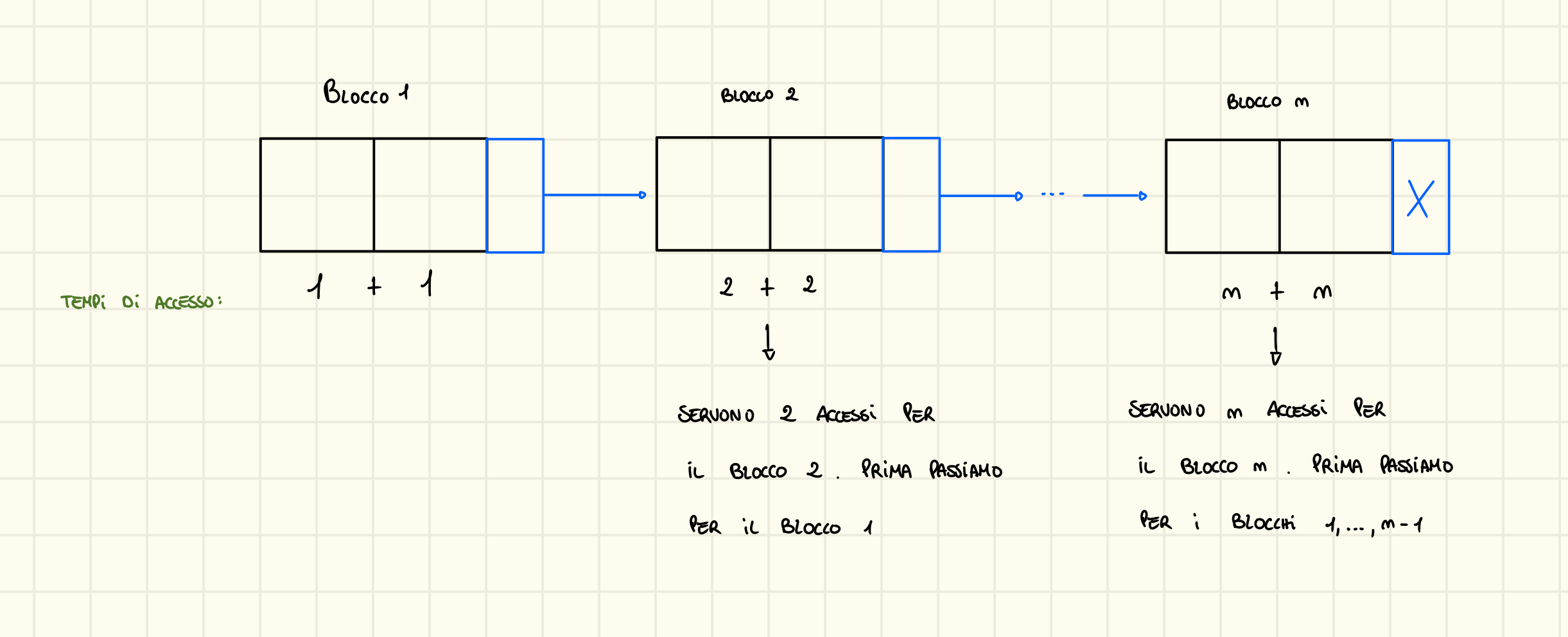
Quindi per ogni record del blocco 2 servono 2 accessi in memoria (scorriamo 2 blocchi) e così via per ogni blocco, per i record del blocco $n$ abbiamo bisogno di $n$ accessi dato che prima scorriamo tutti i precedenti.

Per ottenere il costo medio occorre sommare i costi per accedere ai singoli record e dividere tale somma per il numero di record. Quindi dato che per ogni record degli R record servono i accessi possiamo scrivere:

$$\begin{array}{rl}& \frac{R\cdot 1+R\cdot 2+\dots R\cdot n}{N}=\frac{R(1+2+\cdots +n)}{N}\\ & \\ & \text{Sappiamo che }\frac{N}{R}=n\text{ quindi }\frac{R}{N}=\frac{1}{n}\text{, sostituiamo:}\\ & \\ & \frac{1+2+\cdots +n}{n}=\frac{\sum _{k=1}^{n}k}{n}\\ & \\ & \text{Ricordiamo la sommatoria di Gauss:}\sum _{k=1}^{n}k=\frac{n(n+1)}{2},\text{sostituiamo:}\\ & \\ & \frac{\sum _{k=1}^{n}k}{n}=\frac{n\cdot (n+1)}{n\cdot 2}=\frac{n+1}{2}\approx \frac{n}{2}\end{array}$$

Quindi abbiamo sempre $\frac{n}{2}$ come costo medio.

Se invece vogliamo cercare tutti i record con una determinata chiave che, in questo caso, ammette duplicati allora dovremmo comunque accedere a tutti gli $n$ blocchi dato che non possiamo sapere quando abbiamo trovato l’ultima occorrenza.

Inserimento

Per effettuare l’inserimento abbiamo bisogno di 1 accesso in lettura per portare l’ultimo blocco in memoria principale e un altro accesso in scrittura per riscriverlo in memoria secondaria dopo averlo modificato. Questo accade se ammettiamo duplicati.

Se non ammettiamo duplicati l’inserimento è preceduto da una ricerca e quindi dobbiamo aggiungere una media di $\frac{n}{2}$ accessi per verificare che non esista già un record con quella chiave.

Modifica

Abbiamo come primo costo quello della ricerca, infatti dobbiamo trovare il record, poi dobbiamo aggiungere un accesso in scrittura per riscrivere il blocco in memoria una volta modificato, questo costo va ripetuto per ogni occorrenza della chiave, se ammettiamo duplicati.

Cancellazione

Dobbiamo pagare il costo della ricerca. Se vogliamo evitare “buchi” dobbiamo pagare anche un accesso in lettura in più per leggere l’ultimo blocco e infine 2 accessi in scrittura, uno per riscrivere il blocco modificato e uno per riscrivere l’ultimo blocco dal quale abbiamo spostato l’ultimo record.

File Hash

Questo tipo di file è suddiviso in bucket numerati da 0 a B-1, ciascun bucket è costituito da uno o più blocchi collegati fra loro tramite puntatori e organizzati come un heap. In cima al file c’è la bucket directory che contiene tutti i puntatori per i bucket ovvero B elementi.

Abbiamo quindi una struttura simile:

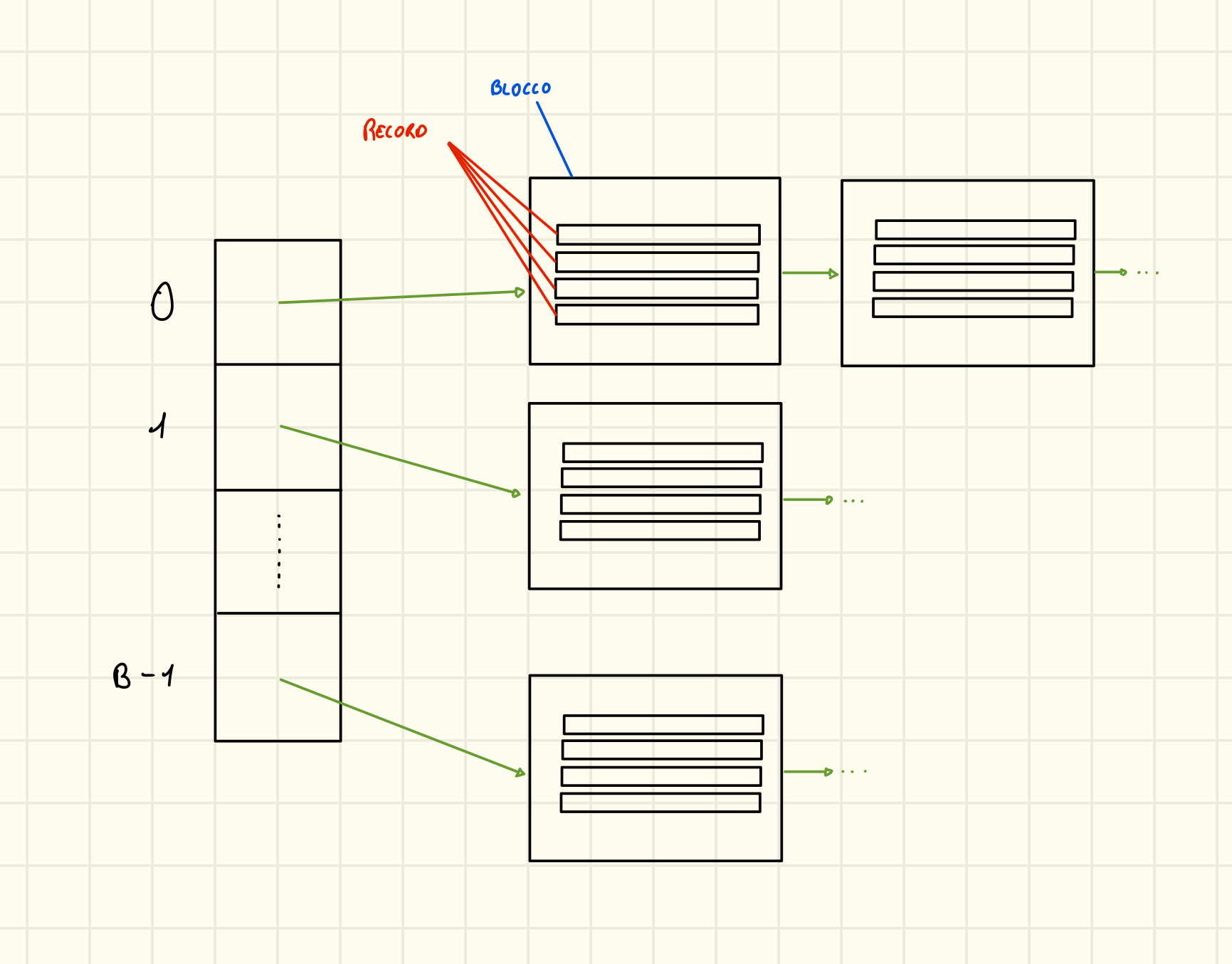
Funzione Hash

Dato un valore v per la chiave, il numero del bucket in cui deve trovarsi un record con chiave v è calcolato mediante una funzione chiamata funzione hash.

Una funzione di Hash per essere “buona” deve suddividere in modo equo i record nei vari bucket, quindi al variare della chiave tutti i bucket devono avere la stessa probabilità di “uscita”. In genere una funzione hash trasforma la chiave in un numero, lo divide per B e fornisce il resto della divisione come numero del bucket (in modo da rimanere limitati al numero di bucket), questo resto è il bucket dove andrà inserito il record.

Esempio Funzione Hash

Trattiamo il valore v della chiave come una sequenza di bit, ad esempio $100101111010$, dividiamo tale sequenza in gruppi di bit uguali fra loro e sommiamo tali gruppi come se fossero interi:

$$1001|0111|1010=9+7+10=26$$

Adesso dividiamo questo risultato per il numero di bucket e prendiamo il resto della divisione, questo sarà il bucket. Ad esempio se $B=3$ allora calcoliamo $26\%3=2$, quindi il record che ha questa chiave andrà inserito nell’ultimo blocco del bucket 2.

Operazioni

Una qualsiasi operazione in un file hash richiede:

• Valutazione della funzione di hash per v, $h(v)$, per individuare il bucket, per noi questo ha costo 0 dato che ci interessano soltanto gli accessi in memoria.
• Esecuzione dell’operazione sul bucket che è organizzato come un heap.

Inoltre dato che l’inserimento di nuovi record viene effettuato sull’ultimo bucket, la bucket directory dovrà contenere anche un puntatore all’ultimo record di ogni bucket oltre che al loro inizio.

Quindi se la funzione di hash distribuisce in modo uniforme i record nei vari bucket avremo che ogni bucket è costituito da $\frac{n}{B}$ blocchi e quindi il costo richiesto da un’operazione è approssimativamente $\frac{1}{B}$ - esimo del costo della stessa operazione eseguita su un file heap.

Osservazioni

Ovviamente più bucket abbiamo più è basso il costo delle operazioni, ma dobbiamo fare delle considerazioni che ci portano a limitare questo numero:

• Ogni bucket deve avere almeno un blocco
• La bucket directory deve avere una dimensione tale da essere mantenuta in memoria principale altrimenti effettueremo accessi per leggere i blocchi della bucket directory.

Osservazioni per esame e corso

• Ogni record deve essere contenuto completamente in un blocco
• I blocchi vengono allocati per intero

File con Indice

Quando le chiavi permettono un ordinamento significativo per l’applicazione ci conviene utilizzare un’organizzazione fisica che ne tiene conto in modo da avere più vantaggi.

Interi e stringhe ammettono i classici ordinamenti, quindi crescente o decrescente e per le stringhe lessicografico. Per i campi multipli si ordina prima sul primo campo poi sul secondo e così via.

Ordine Lessicografico

Un alfabeto finito totalmente ordinato di simboli è un insieme:

$$\Sigma =({\delta }_1,\dots ,{\delta }_n)$$

Dotato di ordine totale, quindi:

$${\delta }_1<{\delta }_2<\cdots <{\delta }_n$$

E date due sequenze di simboli:

$$\begin{array}{r}I={\delta }_{i1}{\delta }_{i2}\dots {\delta }_{in}\\ J={\delta }_{j1}{\delta }_{j2}\dots {\delta }_{jm}\end{array}$$

Diciamo che $I<J$ se esiste un numero $k\in \mathbb{N}$ per cui:

$${\delta }_{i1}{\delta }_{i2}\dots {\delta }_{ik}={\delta }_{j1}{\delta }_{j2}\dots {\delta }_{jk}$$

E vale una delle seguenti relazioni:

$${\delta }_{i(k+1)}<{\delta }_{j(k+1)}\text{ oppure }n=k<m$$

Quindi abbiamo preso due sequenze di simboli tali che fino ad un certo valore $k$ risultano uguali. Diciamo che la sequenza $I$ è minore della sequenza $J$ se il valore successivo a k di $I$ è minore a quello successivo in $J$ oppure se $I$ è una sottosequenza di $J$ e quindi $I$ è completamente contenuta in $J$.

Algoritmo di Confronto

Le condizioni appena viste sono equivalenti al seguente algoritmo:

• Si pone $n=1$
• Si confrontano i simboli nella posizione n-esima della stringa:
  • Se una delle due non possiede l’elemento n-esimo allora è minore dell’altra e terminiamo
  • Se entrambe le stringhe non possiedono l’elemento n-esimo allora sono uguali e l’algoritmo termina
  • Se i simboli sono uguali si passa alla posizione successiva
  • Se questi sono diversi, il loro ordine è l’ordine delle stringhe

File con Indice (sparso)

Il primo esempio è il file ISAM (Indexed Sequential Access Method).

Questo è il file che abbiamo come esempio:

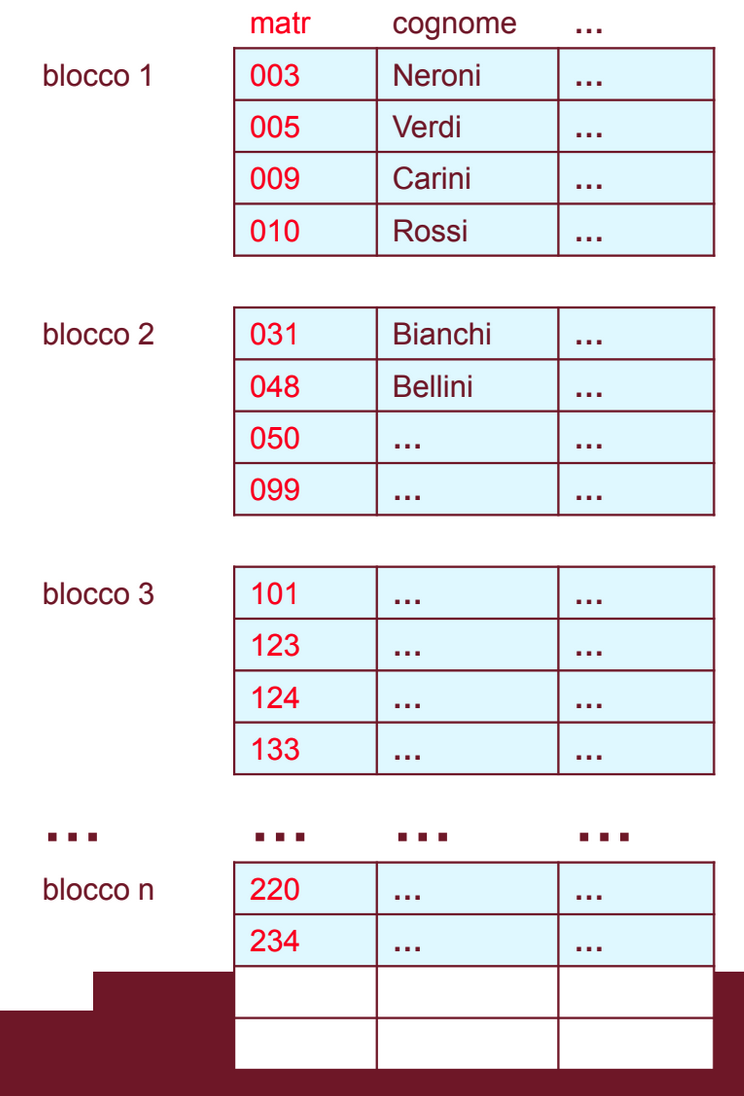
Questo file viene ordinato in base al valore della chiave, in questo caso la matricola. Per fare questo viene creato un nuovo file, il file indice, che contiene un record per ogni blocco del file principale, questi record hanno due campi, uno è il puntatore ad un blocco del file principale e affiancato a questo c’è il valore più piccolo della chiave presente in quel blocco:

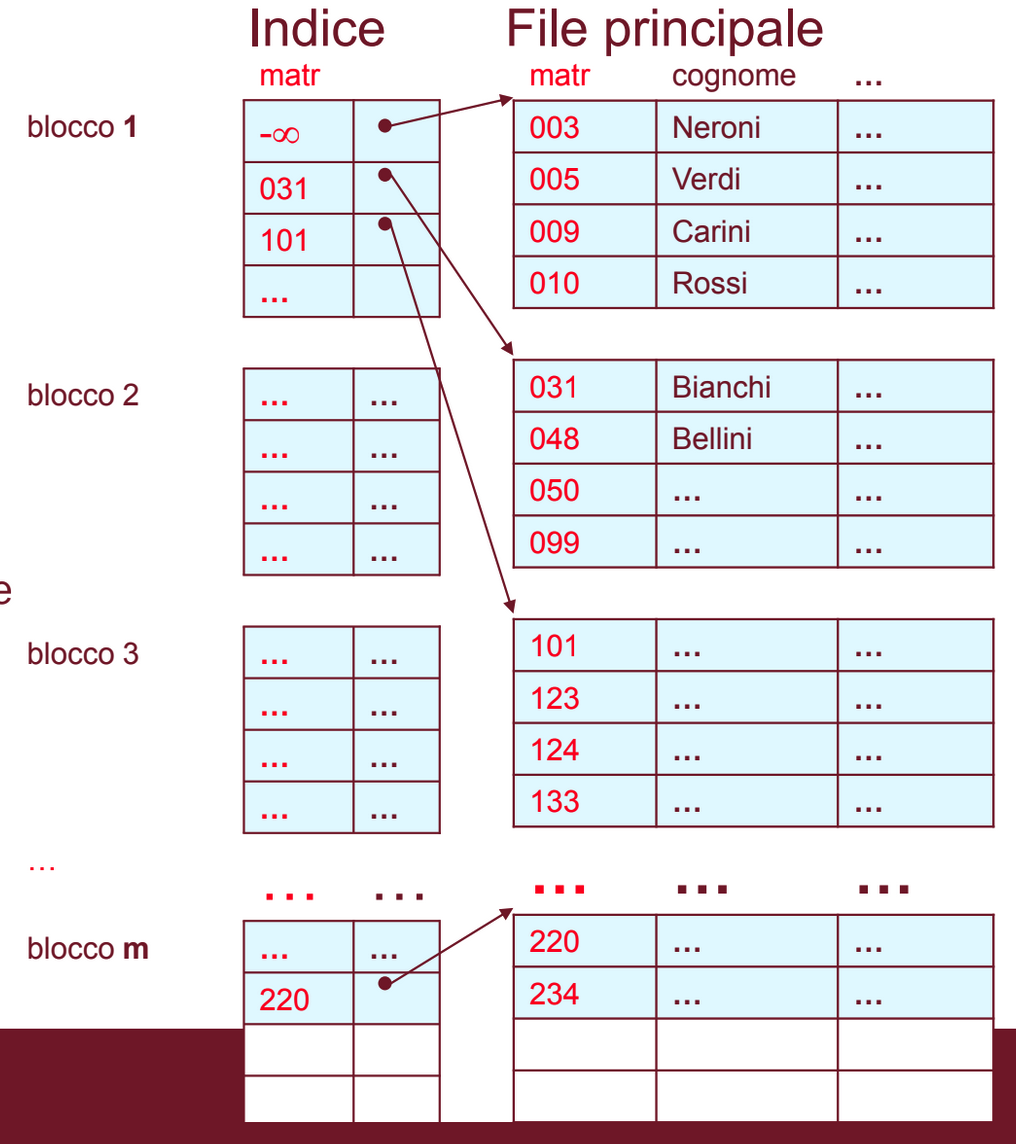
L’indice $-\infty$ è usato solo come notazione per indicare il primo blocco.

Ricerca

Ad esempio il record con chiave 090 deve trovarsi nel blocco del file principale che contiene 031 come valore più piccolo, dato che nel precedente il valore più piccolo è 003 e nei successivi sono $\ge 101$.

Oppure il record con chiave 234 deve trovarsi nell’ultimo blocco del file principale dato che nei precedenti i valori della chiave sono < 220.

Per ricercare un record con valore della chiave $k$ occorre ricercare sul file indice un valore $k^{\prime }$ della chiave che ricopre $k$ cioè tale che:

• $k^{\prime }\le k$
• Se il record con chiave $k^{\prime }$ non è l’ultimo record del file indice e $k^{\prime \prime }$ è il valore della chiave nel record successivo allora $k<k^{\prime \prime }$.

La ricerca di un record con chiave $k$ richiede una ricerca sul file indice più un accesso in lettura sul file principale.

Ricerca Binaria sul file Indice

Dato che il file indice è ordinato in base al valore della chiave, la ricerca di un valore che ricopre la chiave può essere effettuata tramite la ricerca binaria:

• Si fa un accesso in lettura al blocco $\frac{m}{2}+1$ e si confronta $k$ con $k1$ (prima chiave del blocco)
• Se $k=k1$ abbiamo finito
• Se $k<k1$ allora si ripete il procedimento sui blocchi da 1 a $\frac{m}{2}$
• Altrimenti si ripete il procedimento sui blocchi da $\frac{m}{2}+1$ a $m$ (ricontrolliamo anche questo blocco dato che prima abbiamo controllato solo la prima chiave e non il resto del blocco)

Ci si ferma quando lo spazio di ricerca è ridotto ad un unico blocco e quindi dopo $\lceil {\log }_{2}m\rceil$ accessi

Ricerca per Interpolazione

Si basa sulla conoscenza della distribuzione della chiave, abbiamo quindi bisogno di una funzione $f$ che dati tre valori $k1,k2,k3$ della chiave fornisca un valore che è la frazione dell’intervallo di valori della chiave compresi tra $k2$ e $k3$ in cui deve trovarsi $k1$ cioè la chiave che stiamo cercando.

Ad esempio quando andiamo a cercare un valore in un dizionario non partiamo sempre da metà ma se ad esempio cerchiamo una parola con la C cercheremo in una zona vicina all’inizio.

• $k1$ deve essere confrontato con il valore $k$ della chiave nel primo record del blocco $i$ del file indice, dove $i=f(k1,k2,k3)\ast m$
• Se poi $k1$ è minore di tale valore allora il procedimento deve essere ripetuto sui blocchi $1,2,\dots ,i-1$ mentre se è maggiore lo ripetiamo sui blocchi $i,i+1,\dots ,m$ finché la ricerca si restringe ad un unico blocco.

La ricerca per interpolazione richiede circa $1+{\log }_2({\log }_{2}m)$ accessi è quindi molto più veloce ma è anche molto difficile conoscere la $f$ e poi dobbiamo anche considerare che la distribuzione dei dati potrebbe cambiare nel tempo, possiamo quindi utilizzarla solo su strutture statiche nel tempo.

Esempio pratico

Supponiamo di avere un array ordinato: $[10,20,30,40,\dots ,90,100]$ e vogliamo cercare il valore 55.

Prendiamo quindi il valore minimo 10 e il massimo 100 e calcoliamo la posizione stimata con la seguente funzione (che può variare da caso a caso):

$$i=inizio+(\frac{v_1-v_2}{v_3-v_2})\cdot (fine-inizio)$$

Quindi sostituendo:

$$0+(\frac{55-10}{100-10})\cdot (9-0)=4.5$$

Adesso a seconda della funzione scegliamo se prendere 4 o 5 come indice e confrontiamo il valore di questo indice con il valore della chiave. Se combaciano abbiamo finito altrimenti se la chiave è più piccola ripetiamo il procedimento sulla metà inferiore o se più grande su quella superiore.

Inserimento

Per effettuare un inserimento dobbiamo sicuramente pagare il costo della ricerca + 1 accesso per scrivere il blocco modificato se nel blocco c’è spazio per inserirlo altrimenti possiamo seguire diverse strategie e abbiamo bisogno di più accessi (consideriamo B il blocco dove inserire il record):

• Se c’è spazio nel blocco successivo o nel precedente, il nuovo record o un record che era nel blocco pieno diventano il primo record del successivo e quindi modifichiamo anche il valore affiancato al record nel file indice.

• Se non c’è spazio né nel precedente né nel successivo dobbiamo richiedere un nuovo blocco che seguirà B al file system e dobbiamo ripartire i record tra B e il nuovo blocco, sarà necessario quindi inserire un nuovo record nel file indice relativo al nuovo blocco:

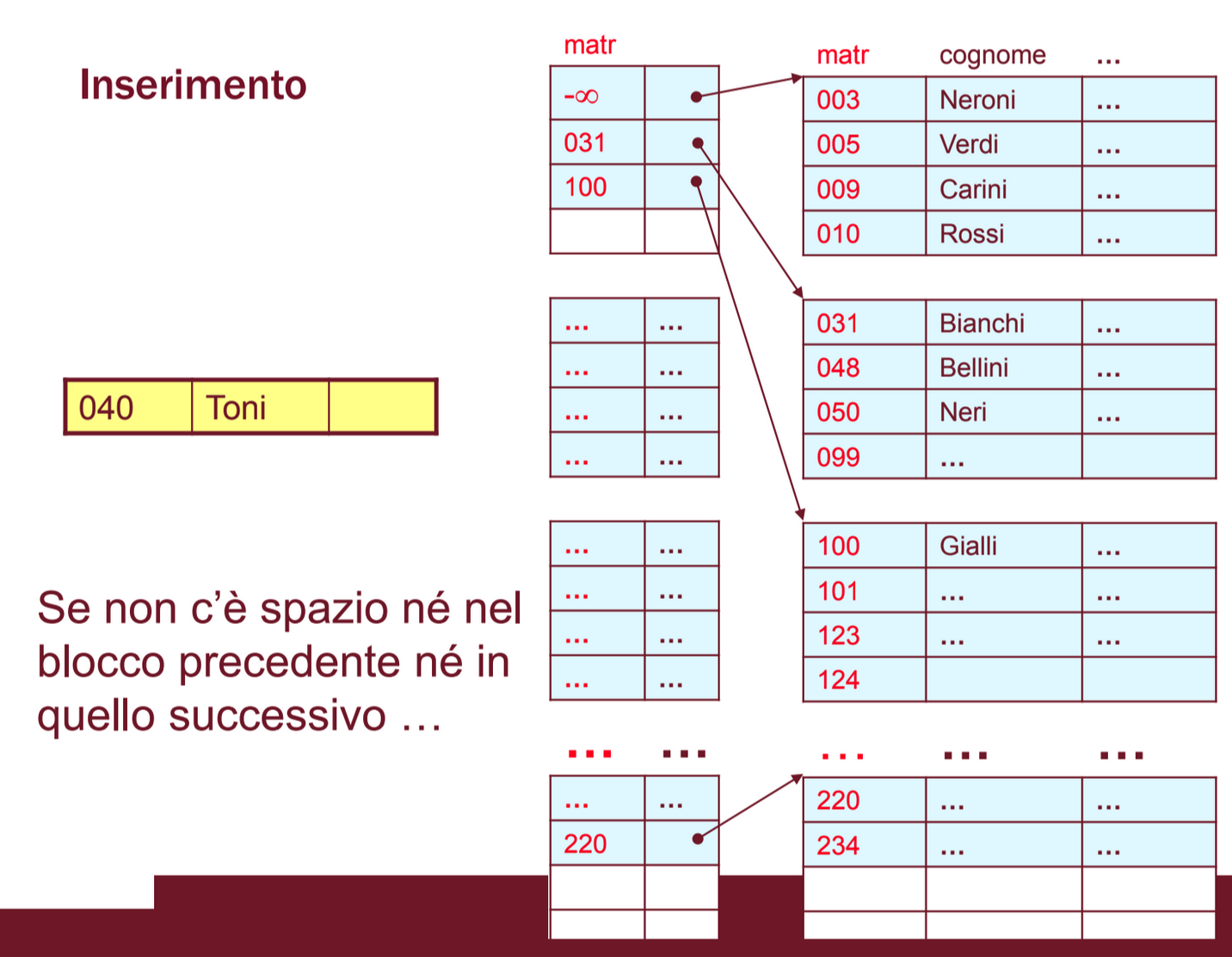
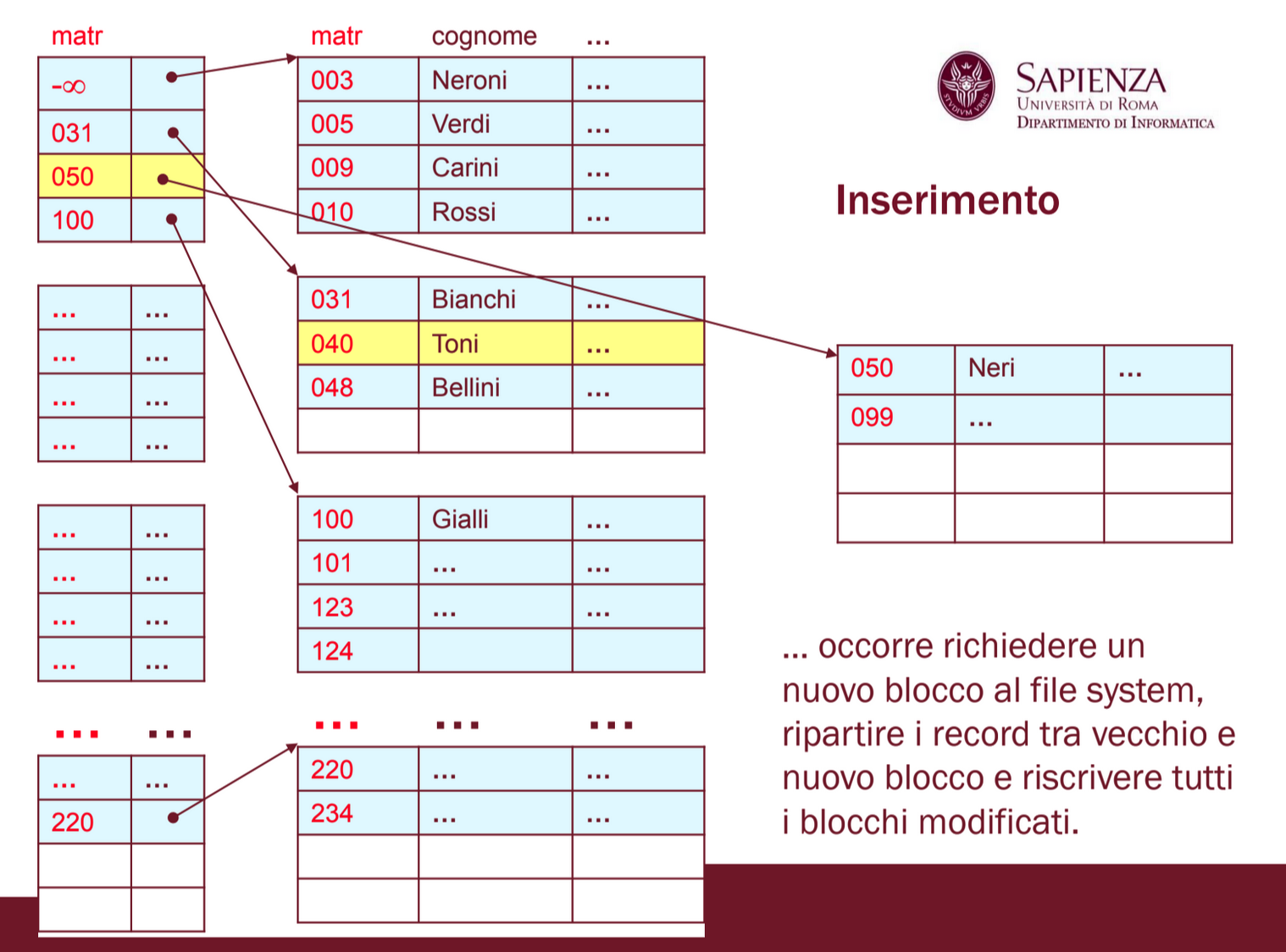  In ogni caso occorre modificare i bit usato / non usato nelle intestazioni dei blocchi

Cancellazione

Ci serve ovviamente il costo della ricerca + 1 accesso per modificare il blocco.

Se il record cancellato è il primo di un blocco abbiamo bisogno di ulteriori accessi per modificare il record nel file indice.

Se il record cancellato era l’unico del blocco, il blocco viene restituito al sistema e nel file indice cancelliamo il record relativo (anche in questo caso se il record è l’unico del blocco lo restituiamo al sistema).

In ogni caso occorre modificare i bit di usato / non usato nelle intestazioni dei blocchi.

Modifica

Come prima cosa occorre cercare il record poi distinguiamo due casi:

• Se la modifica non coinvolge i campi della chiave, il record viene modificato e il blocco riscritto.
• Altrimenti la modifica equivale ad una cancellazione seguita da un inserimento.

B-Tree

È una generalizzazione del file indice dove accediamo attraverso una gerarchia di file indice. L’indice a livello più alto viene detto radice ed é costituito da un singolo blocco, possiamo quindi caricarlo in RAM durante l’utilizzo del file.

Ogni blocco di un file indice é costituito da record contenenti una coppia $(v,b)$ dove $v$ è il valore della chiave del primo record della porzione di file principale accessibile attraverso il puntatore $b$, questo puntatore però può puntare anche ad un blocco del file indice a livello immediatamente più basso oppure ad un blocco del file principale.

In ogni file indice possiamo risparmiare spazio memorizzando, per il primo record, soltanto il puntatore infatti non ci serve sapere il valore più basso che troveremo, se dobbiamo cercare un valore più piccolo di quello presente nel secondo record lo andremo a cercare sicuramente nel primo.

Ogni blocco del file principale è memorizzato come quello di un ISAM.

Ogni blocco di un B-Tree sia indice che file principale, deve essere pieno almeno per metà tranne eventualmente la radice.

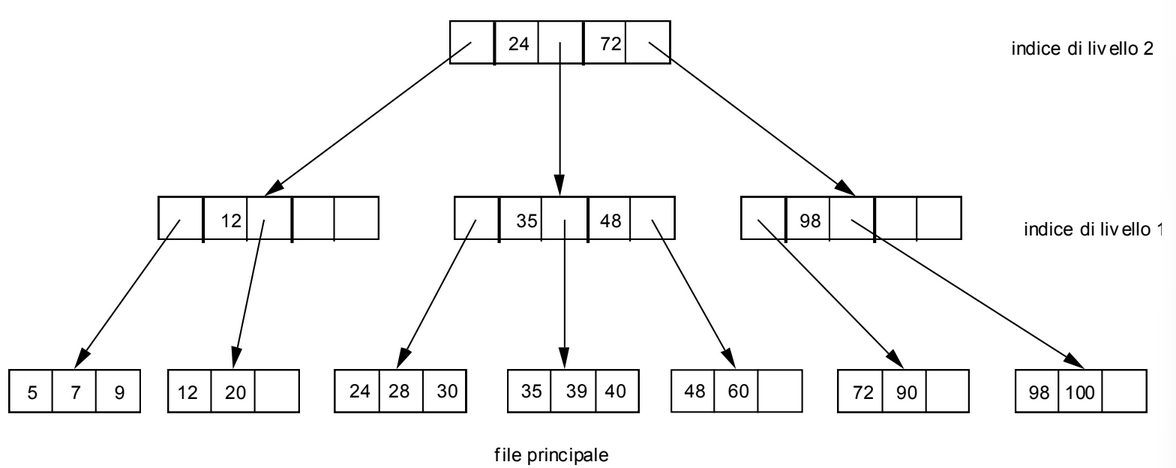
Notiamo che nei blocchi dei file indice non è mai presente il primo record per intero infatti manca il valore associato all’indirizzo ma come detto prima non ci serve.

Ricerca

Per cercare un record con un dato valore si accede agli indice di livello più alto e si scende nei livelli più bassi restringendo la porzione del file principale in cui potrebbe trovarsi il record in un unico blocco.

Partiamo quindi dalla radice ed esaminiamo blocco per blocco, se il blocco esaminato è un blocco del file principale allora quello è il blocco in cui potrebbe trovarsi il record, se invece è un blocco del file indice si cerca in quel blocco un valore della chiave che ricopre il valore che stiamo cercando e poi si segue il puntatore associato a quel valore proseguendo così in un altro livello.

Per la ricerca sono necessari quindi $h+1$ accessi dove $h$ è l’altezza dell’albero.

Osservazione

Più i blocchi sono pieni più sarà piccolo $h$ e quindi meno costerà la nostra ricerca e per questo chiediamo che i blocchi siano pieni almeno per metà. Ma se i blocchi sono completamente pieni un inserimento può richiedere una modifica dell’indice ad ogni livello e in alcuni casi far crescere l’altezza di un livello.

Esempio

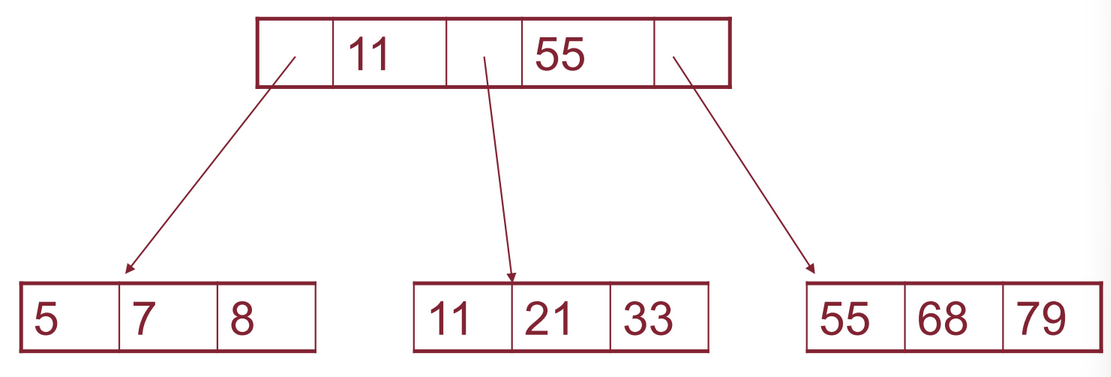
Vogliamo inserire in questo albero il record con chiave 40, dobbiamo quindi riorganizzare la struttura:

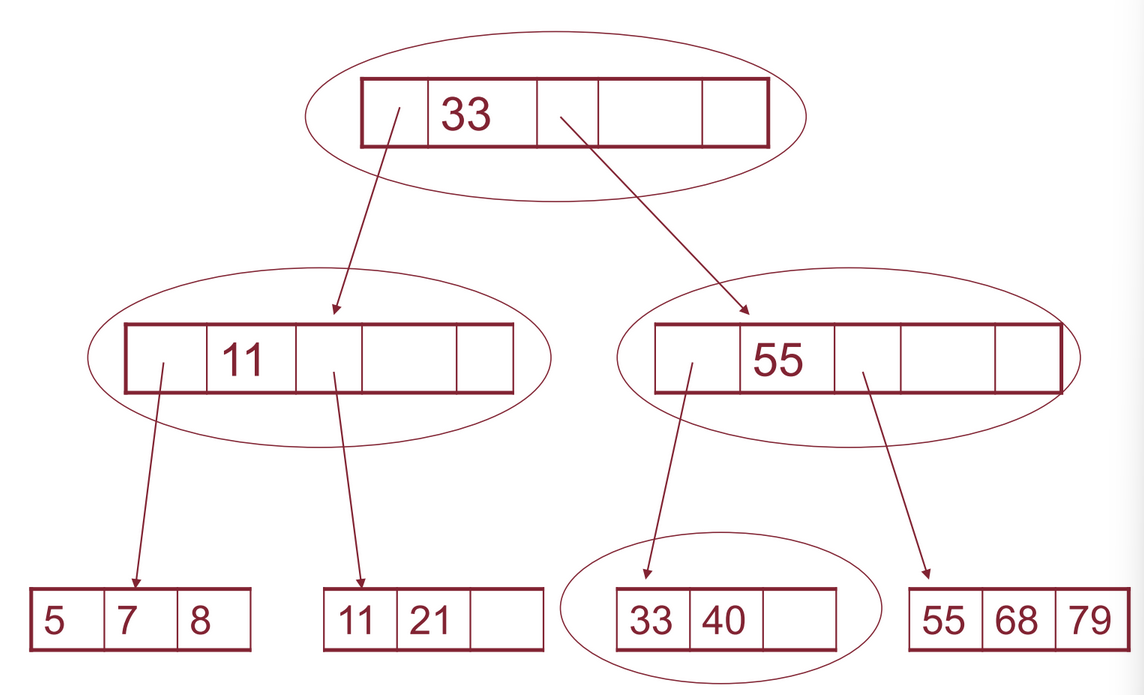
In questo modo abbiamo anche i blocchi non completamente occupati.

Ma qual è il massimo valore che può assumere $h$ nel caso peggiore?

Definiamo:

• $N$ numero di record nel file principale
• $2e-1$ numero di record del file principale che possono essere memorizzati in un blocco
• $2d-1$ numero di record del file indice che possono essere memorizzati in un blocco

Li rendiamo dispari per rendere semplici i calcoli

Siccome vogliamo che i blocchi siano pieni almeno per metà:

• Ogni blocco del file principale deve contenere almeno $e$ record
• Ogni blocco del file indice deve contenere almeno $d$ record

L’altezza massima dell’albero denotata con $k$ si ha quando i blocchi sono pieni al minimo e quindi quando i blocchi hanno esattamente il numero di elementi scritti sopra quindi $e$ per quelli del principale e $d$ per l’indice.

Quindi:

• Il file principale ha al massimo $\frac{N}{e}$ blocchi
• Al livello 1 il file indice ha $\frac{N}{e}$ record che possono essere memorizzati in $\frac{N}{ed}$ blocchi
• Al livello 2 il file indice ha $\frac{N}{ed}$ record possono essere memorizzati in $\frac{N}{e{d}^2}$ blocchi
• …
• Al livello $i$ il file indice ha $\frac{N}{e{d}^{i-1}}$ record che possono essere memorizzati in $\frac{N}{e{d}^i}$ blocchi.

Al livello $k$ che abbiamo detto essere il massimo, il file indice ha esattamente 1 blocco e quindi:

• $\frac{N}{e{d}^k}\le 1$, nelle divisioni prendiamo la parte intera superiore e quindi $\lceil \frac{N}{e{d}^k}\rceil =1$, consideriamo quindi per semplicità l’uguaglianza $e{d}^k=N$ da cui troviamo che $d^k=\frac{N}{e}$ e infine:

$$k={\log }_d\left(\frac{N}{e}\right)$$

Che rappresenta un valore che approssima sufficientemente il limite superiore per l’altezza dell’albero.

Inserimento

La ricerca costa $h+2$ ovvero il costo dell’accesso per cercare il blocco in cui deve essere inserito il record ($h+1$) + 1 accesso per riscrivere il blocco ma questo se nel blocco c’è spazio sufficiente per inserire il record.

Infatti se non c’è spazio nel blocco abbiamo il costo della ricerca $h+1$ e poi dobbiamo aggiungere $s$ accessi dove $s\le 2h+1$ infatti nel caso peggiore per ogni livello dobbiamo sdoppiare un blocco e quindi effettuare due accessi più uno alla fine per la nuova radice.

Vediamo quindi questo esempio più particolare:

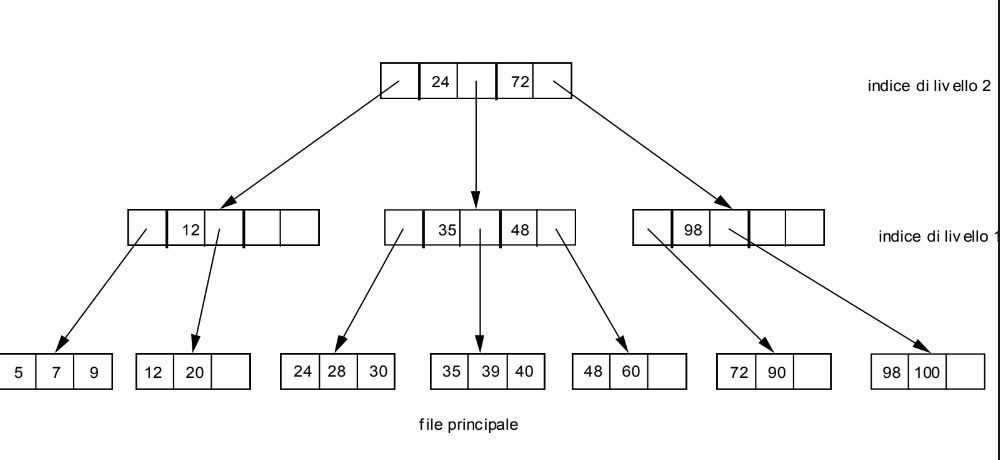
Vogliamo inserire il record con chiave 25 ma notiamo che il blocco in cui dovrebbe trovarsi è pieno, dobbiamo quindi riorganizzare la struttura sdoppiando dei blocchi:

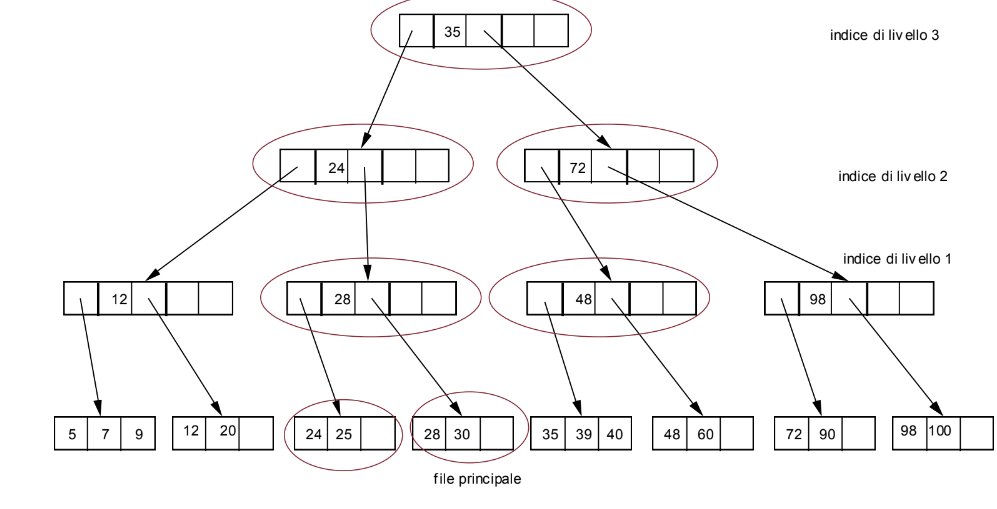
In questo modo i blocchi sono pieni almeno per metà e hanno anche spazio aggiuntivo per contenere successivi inserimenti.

Cancellazione

Abbiamo come sempre il costo della ricerca quindi $h+1$ e poi dobbiamo aggiungere un accesso per riscrivere il blocco modificato, ma questo solo se il blocco rimane pieno per almeno metà dopo la cancellazione altrimenti sono necessari ulteriori accessi.

Esempio

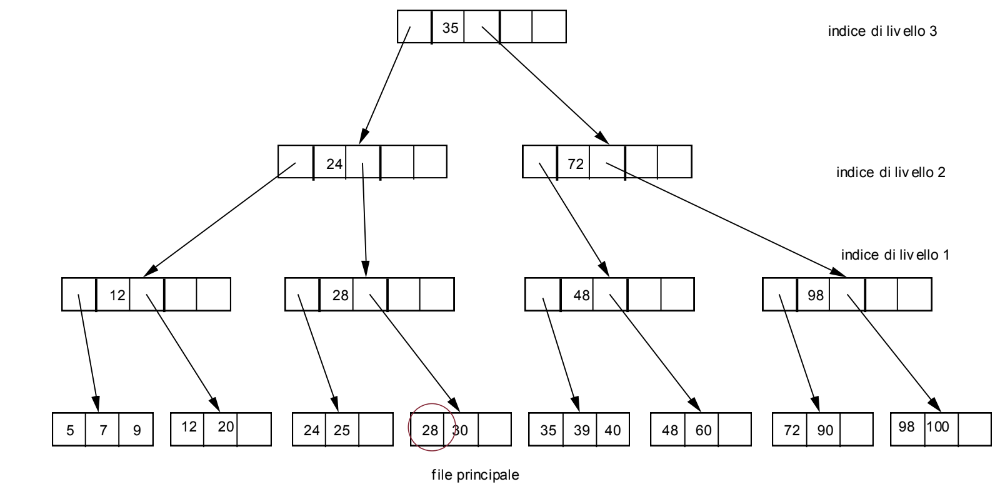
Vogliamo cancellare il record con chiave 28 ma se lo facciamo quel blocco rimane con meno della metà dello spazio occupato, quindi riorganizziamo la struttura:

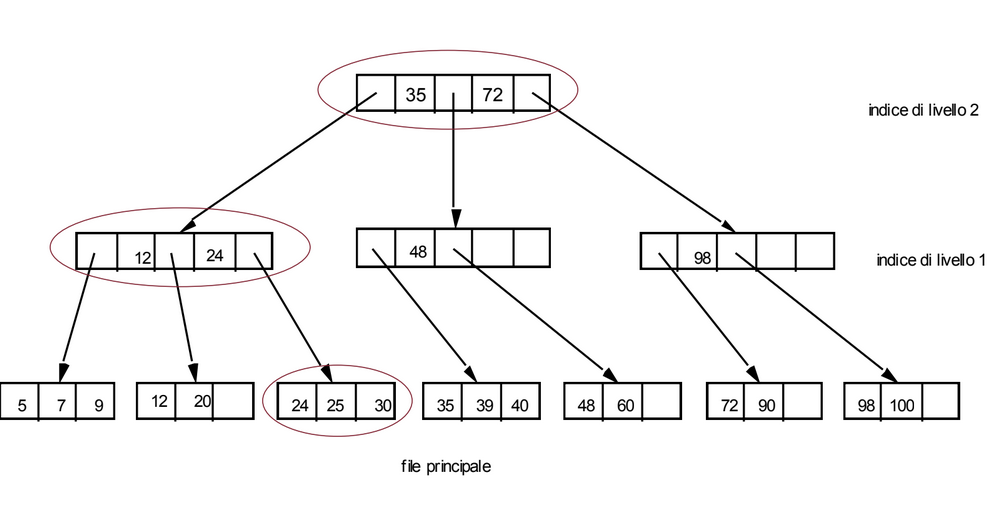
Modifica

Abbiamo sempre il costo della ricerca $h+1$, dobbiamo aggiungere un accesso per riscrivere il blocco se la modifica non coinvolge i campi della chiave altrimenti se li coinvolge abbiamo anche il costo della cancellazione e quello di un inserimento, infatti equivale a cancellare il record e inserirne uno nuovo.

Osservazioni

In un B-tree, per definizione, ogni blocco è sempre pieno almeno per metà (metà spazio fisico ovvero i byte) e quindi andrebbe sempre verificata questa condizione.

Per quanto riguarda il file principale:

• Se il numero di record massimo è dispari e quindi esprimibile come abbiamo fatto con $2e-1$ allora possiamo considerare $e$ come occupazione minima.
• Se il numero di record massimo è pari e quindi esprimibile come $2e$ allora consideriamo $e+1$ come occupazione minima, tranne nel caso in cui la taglia del record è esattamente un sottomultiplo di quella del blocco e quindi la metà dei record riempie esattamente la metà dei byte.

Per il file indice valgono le stesse regole ma dobbiamo fare attenzione al fatto che nei blocchi, il primo record contiene solo un puntatore e quindi vanno eseguiti dei calcoli diversi.