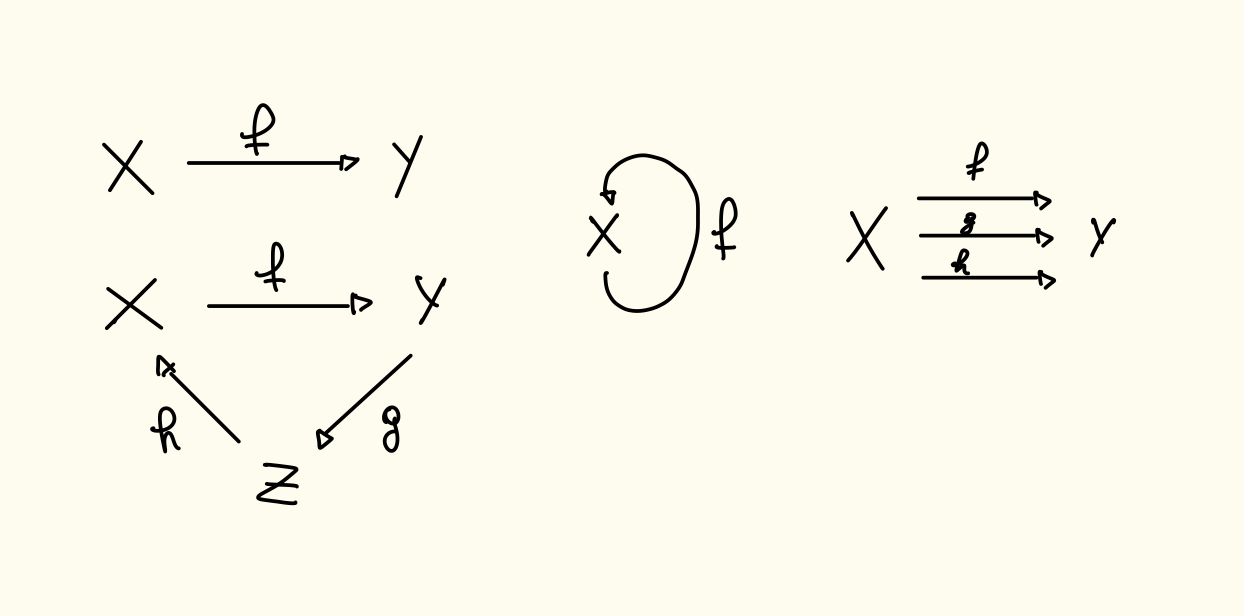Algebra

Ripasso Teoria degli Insiemi

Possiamo vedere un insieme in modo generico come una collezione di elementi, per rappresentarli possiamo o descrivere chi ci appartiene o enumerare tutti gli elementi:

{Rosso, Nero} → Insieme dei due colori Rosso e Nero {0, 1, 2, …} = $\mathbb{N}$ Insieme dei numeri naturali (non si usa questa convenzione di solito)

Poi c’è un insieme particolare chiamato Insieme Vuoto, si indica con $\varnothing$ e non ha nessun elemento al suo interno, inoltre questo è contenuto in tutti gli altri insiemi.

Per indicare un insieme il modo più utilizzato è quello di scegliere un insieme universo U e caratterizzare dei suoi sottoinsiemi attraverso delle proprietà, quindi gli elementi che rispettano tali proprietà faranno parte dei sottoinsiemi.

Esempio

$U=\mathbb{N}$ $I=\{x\in \mathbb{N}:\text{ x eˋ pari }\}$ L’insieme $I$ è formato da tutti gli elementi appartenenti ad $\mathbb{N}$ tali che siano pari.

Inclusione di Insiemi

Dati due insiemi $I,J$ sottoinsiemi di $U$, I si dice sottoinsieme di $J$ se tutti i suoi elementi appartengono a $J$:

$$I\subset J\leftrightarrow \forall x\in I,x\in J$$

La negazione si indica con:

$$I\not\subset J\leftrightarrow \exists x\in I,x\notin J$$

Insiemi Comparabili

Dati due insiemi $I,J\subset U$, si dicono comparabili se $I\subset J\bigvee J\subset I$ è vera. Se invece è vera $I\subset J\bigwedge J\subset I$ allora i due insiemi sono uguali.

Operazioni sugli Insiemi

Dati due insiemi $I,J\subset U$:

• Intersezione: sono gli elementi in comune fra i due insiemi

$$I\cap J=\{x\in U:x\in I\wedge x\in J\}$$

• Unione: sono gli elementi presi da entrambi gli insiemi

$$I\cup J=\{x\in U:x\in I\vee x\in J\}$$

Esempio

$I\subset \mathbb{N}=\{x\in \mathbb{N}:x\text{ eˋ pari}\}$ $J\subset \mathbb{N}=\{x\in \mathbb{N}:x\text{ eˋ dispari}\}$

$I\cup J=\mathbb{N}$ mentre $I\cap J=\varnothing$. Perché?

Algoritmo della Divisione Euclidea per 2

$$x\in \mathbb{N}\text{ Significa che }\exists !(q,r)\in \mathbb{Z}\times \mathbb{N}\text{ t.c. }x=2q+r\text{ con }0\le r\le 1$$

Infatti i numeri interi si dividono in pari o dispari, ovvero possono avere o resto 0 o resto 1, per dimostrarlo supponiamo per assurdo che esista un $x\in I\cap J$ questo significa che:

$$\begin{array}{r}x=2q=2q^{\prime }+1\\ 2(q-q^{\prime })=1\end{array}$$

Impossibile

Diagrammi di Venn

Sono un modo per rappresentare graficamente gli insiemi.

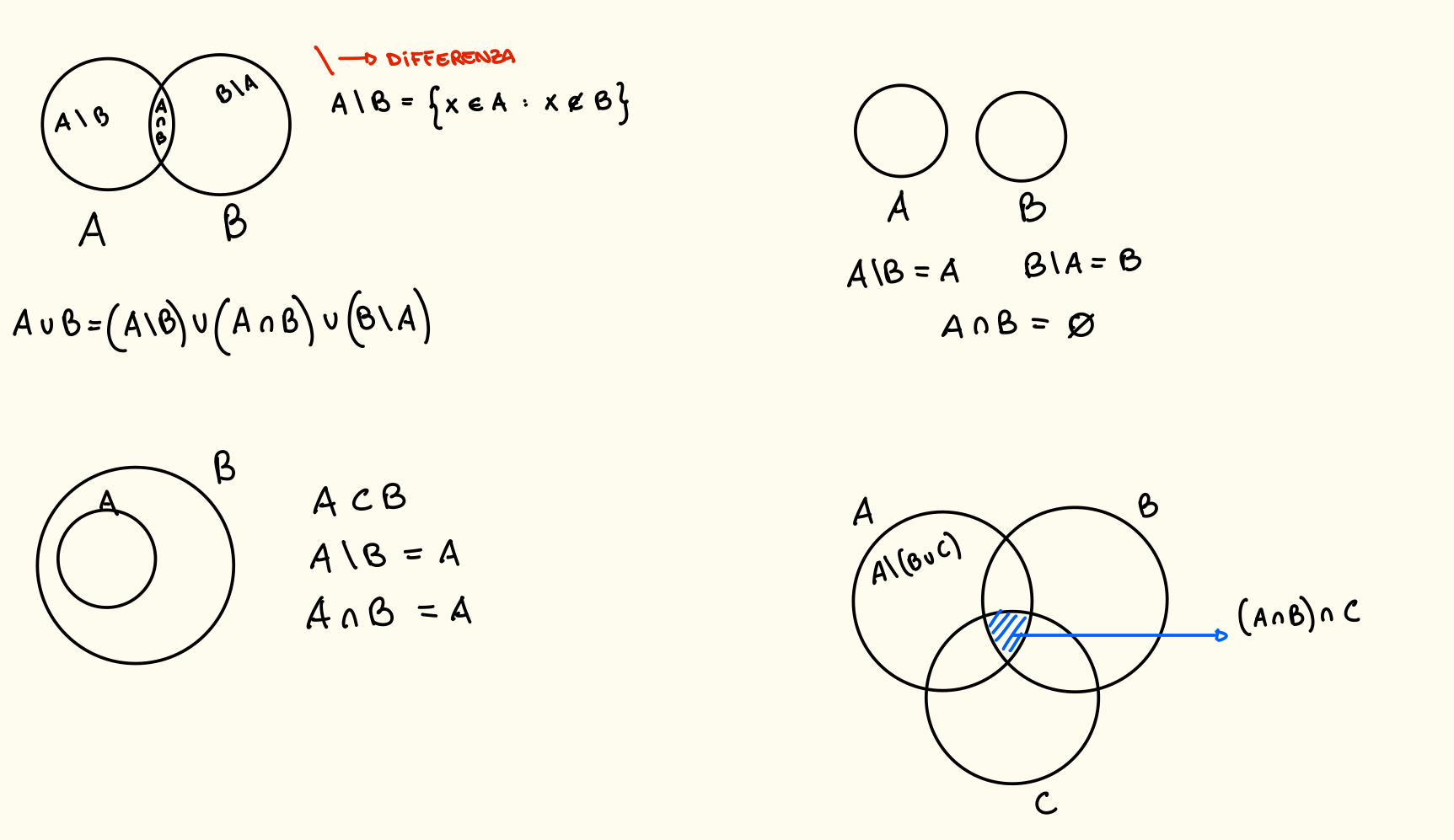
Per indicare gli insiemi possiamo anche utilizzare le tavole di verità basate sulle loro proprietà, utili per verificare alcune proprietà.

P	Q	R
0	0	0
0	0	1
0	1	0
0	1	1
1	0	0
1	0	1
1	1	0
1	1	1

Dalla tabella notiamo quindi che esistono 8 regioni nel nostro diagramma, una per ogni riga, infatti disegnandolo:

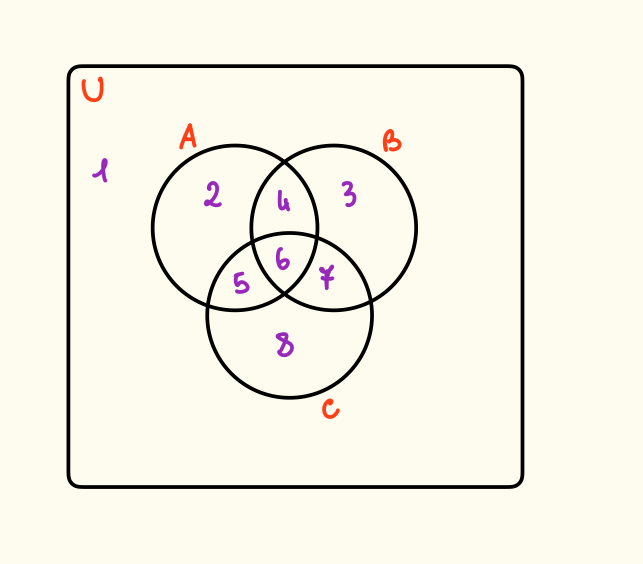
P, Q ed R sono rispettivamente le proprietà di A, B e C. Quindi a seconda del $n$ numero di insiemi abbiamo $2^n$ regioni.

I diagrammi di Venn hanno un limite infatti con dei soli cerchi non è possibile disegnare 4 insiemi o più, questo perché non rappresenteremo tutte le zone e avremo bisogno di figure più complesse.

Terminologia

$A\bigsqcup B$ indica l’unione di due insiemi nel caso in cui $A\cap B=\varnothing$.

Esempio

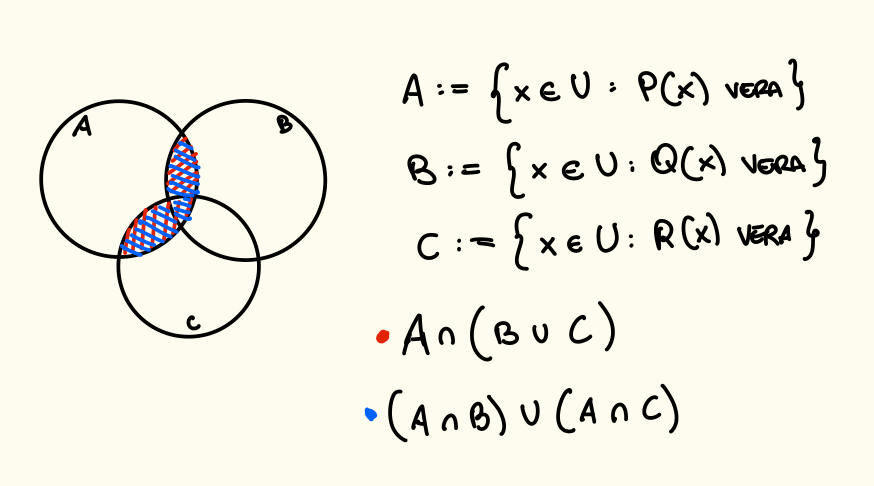
Notiamo che le zone colorate delle due proprietà che abbiamo scritto sono uguali, dimostriamolo anche con la tavola di verità, ricordando che:

• In caso di Congiunzione (and) si fa il prodotto.
• In caso di Disgiunzione (or) si fa il massimo.

$\begin{array}{cccccccc}P& Q& R& Q\vee R& P\wedge (Q\vee R)& P\wedge Q& P\wedge R& (P\wedge Q)\vee (P\wedge R)\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 1& 0& 0& 0& 0\\ 0& 1& 0& 1& 0& 0& 0& 0\\ 0& 1& 1& 1& 0& 0& 0& 0\\ 1& 0& 0& 0& 0& 0& 0& 0\\ 1& 0& 1& 1& 1& 0& 1& 1\\ 1& 1& 0& 1& 1& 1& 0& 1\\ 1& 1& 1& 1& 1& 1& 1& 1\end{array}$

Anche le due tabelle di verità sono uguali quindi significa che gli insiemi sono uguali, caratterizzati dalla stessa proprietà.

Queste infatti prendono il nome di Leggi di De Morgan.

1. $A\cap (B\cup C)=(A\cap B)\cup (A\cap C)$
2. $A\cup (B\cap C)=(A\cup B)\cap (A\cup C)$

Prodotto Cartesiano

Dati due insiemi $X,Y$ non vuoti si definisce $X\times Y=\{(x,y):x\in X,y\in Y\}$. Con la scrittura ${\mathbb{R}}^2$ indichiamo $\{(x,y):x,y\in \mathbb{R}\}$. Il prodotto cartesiano è formato da coppie ordinate quindi non confondiamo $(x,y)$ con $\{x,y\}$.

Si pone $(x,y)=\{x,\{x,y\}\}$. Infatti anche nell’insieme non possiamo scambiare $x,y$ altrimenti cambiamo significato a quest’ultimo.

Se aggiungiamo un elemento: $(x,y,z)=(x,(y,z))=(x,\{y,\{y,z\}\})=\{x,\{x,\{y,\{y,z\}\}\}\}$.

Questo serve per definire il concetto di ordine usando gli insiemi, una struttura dove l’ordine non conta. Abbiamo quindi rappresentato una coppia ordinata, mantenendo l’ordine, con un insieme.

Altre notazioni:

• ${\mathbb{R}}^n:=\mathbb{R}\times {\mathbb{R}}^{n-1}$
• ${\mathbb{R}}^1:=\mathbb{R}$

Corrispondenze

Prendiamo due insiemi $X,Y\ne \varnothing$, una corrispondenza su $X$ e $Y$ è il dato:

$$(X,Y,\Gamma )\subset (X,Y,X\times Y)$$

Dove:

• $X$ indica il dominio
• $Y$ indica il codominio
• $\Gamma$ è un sottoinsieme non vuoto di $X\times Y$ detto “grafo”.

Relazioni

Una relazione è una corrispondenza dove dominio e codominio coincidono quindi $(X,X,\Gamma )$, possiamo anche scrivere $(X,\Gamma )$.

Definiamo $R=(X,\Gamma )$, quindi $\Gamma$ sarà un sottoinsieme di $X^2$, presi due elementi $x,y\in X$ si dicono in relazione se:

$$xRy\iff (x,y)\in \Gamma$$

La parte a sinistra è una convenzione per dire che $x$ è in relazione con $y$.

Proprietà delle Relazioni:

• Riflessiva: $R$ è riflessiva se $\forall x\in X$ abbiamo che $xRx$ (oppure che $\forall x\in X,(x,x)\in \Gamma$).
• Simmetrica: $R$ è simmetrica se $\forall x,y\in X$ se $xRy$ allora $yRx$ (oppure se $(x,y)\in \Gamma$ allora anche $(y,x)\in \Gamma$).
• Transitiva: $R$ è transitiva se presi 3 elementi $x,y,z\in X$, se $xRy\wedge yRz\Rightarrow xRz$.
• Equivalenza: $R$ è una relazione di equivalenza se è contemporaneamente Riflessiva, Simmetrica e Transitiva.

Esempio 1 - Relazione d’uguaglianza

Si prenda $R=(\mathbb{R},\Delta )$ dove $\Delta =\{(x,x):x\in \mathbb{R}\}$. Al posto di scrivere $R$ scriviamo $=$.

• $=$ è riflessiva infatti $\forall x\in \mathbb{R},x=x$
• $=$ è simmetrica infatti $\forall x,y\in \mathbb{R},x=y\Rightarrow y=x$
• $=$ è transitiva infatti $\forall x,y,z\in \mathbb{R},x=y\wedge y=z\Rightarrow x=z$

Esempio 2 - Rette parallele

$X=\{\text{rette di }{\mathbb{R}}^2\}$

Dati $r,r^{\prime }\in X$ abbiamo che $r||r^{\prime }\iff$ $r$ e $r^{\prime }$ sono parallele.

• || è riflessiva: Ogni retta è parallela a se stessa
• || simmetrica: Se $r||r^{\prime }$ allora anche $r^{\prime }||r$
• || transitiva: Se $r||r^{\prime }$ e $r^{\prime }||r^{\prime \prime }$ allora $r||r^{\prime \prime }$

Dimostrazione della transitività:

Vettori

Quando indichiamo $(x^{\prime },y^{\prime })\in {\mathbb{R}}^2$ stiamo indicando dei vettori, se li sommiamo alla retta non cambiamo il suo coefficiente angolare e rimangono quindi parallele, infatti data l’equazione di una retta:

$$y=mx+q$$

Se sommiamo un vettore otteniamo:

$$y^{\prime }=m(x+x^{\prime })+(q+y^{\prime })$$

Notiamo quindi che $m$, il coefficiente angolare, è rimasto invariato.

• $r||r^{\prime }\iff r^{\prime }=r+(x^{\prime },y^{\prime })$ con $(x^{\prime },y^{\prime })\in {\mathbb{R}}^2$.
• $r^{\prime }||r^{\prime \prime }\iff r^{\prime \prime }=r^{\prime }+(x^{\prime \prime },y^{\prime \prime })$ con $(x^{\prime \prime },y^{\prime \prime })\in {\mathbb{R}}^2$

Queste due condizioni implicano che:

• $r^{\prime \prime }=r+(x^{\prime },y^{\prime })+(x^{\prime \prime },y^{\prime \prime })$ ovvero $r^{\prime \prime }=r+(x^{\prime }+x^{\prime \prime },y^{\prime }+y^{\prime \prime })$

Quindi dato che $r^{\prime \prime }$ è formata da $r$ traslata sul piano da un vettore e mantenendo quindi la stessa pendenza abbiamo che anche $r||r^{\prime \prime }$.

Esempio 3 - Rette Ortogonali

$X=\{\text{rette di }{\mathbb{R}}^2\}$

Date $r,r^{\prime }\in X$, abbiamo che $r\perp r^{\prime }\iff r,r^{\prime }$ sono ortogonali.

In questo caso:

• $\perp$ è simmetrica
• $\perp$ non è riflessiva
• $\perp$ non è transitiva

Esempio 4 - Minore o Uguale

$X=\mathbb{R}$, dati due elementi $x,y\in X$ abbiamo che $xRy\iff x\le y$

• Riflessiva, $\forall x,x\le x$
• Transitiva, $\forall x,y,z$ se $x\le y\wedge y\le z$ allora $y\le z$
• Non è simmetrica, $2\le 3$ ma $2\nleqq 3$

Però è:

• Antisimmetrica: $\forall x,y\in X,x\le y\wedge y\le x\iff x=y$
• Totale: $\forall x,y\in \mathbb{R}$ o $x\le y$ o $y\le x$

Relazione Antisimmetrica

Presi qualsiasi due elementi $x,y$ se $x$ è in relazione con $y$ e $y$ e in relazione con $x$ allora $x=y$.

$$\forall x,yxRy\wedge yRx\iff x=y$$

Relazione Totale

Tutti gli elementi sono in relazione con almeno un altro elemento.

$$\forall x,y\in \mathbb{R}xRy\vee yRx$$

Notiamo che l’inclusione come relazione è, come il minore o uguale, riflessiva, antisimmetrica e transitiva ma non totale.

Studio delle Relazioni d’equivalenza

Sia $R=(X,\Gamma )$ relazione d’equivalenza e $x\in X$, poniamo $Cl(x)=\{y\in Xt.c.xRy\}$.

$Cl$ è la classe di equivalenza di un elemento e da notare che non può essere vuota $Cl(x)\ne \varnothing$ infatti dato che siamo in una relazione d’equivalenza $x$ è in relazione con se stesso e quindi $x\in Cl(x)$ ovvero $xRx$.

L’elemento $x$ si chiama rappresentante della classe d’equivalenza, infatti si può avere che $Cl(x)=Cl(x^{\prime })$ con $x\ne x^{\prime }$.

Proposizione 1

Data $R=(X,\Gamma )$ una relazione d’equivalenza abbiamo che:

1. Se $x,y\in X$, allora $Cl(x)=Cl(y)\iff xRy$
2. $\forall x,y\in X$ allora:
   1. o $Cl(x)=Cl(y)$
   2. oppure $Cl(x)\cap Cl(y)=\varnothing$

Quindi due classi di equivalenza di una relazione d’equivalenza o sono uguali o sono disgiunte, inoltre data una classe d’equivalenza $C,\forall x\in C,C=Cl(x)$ ovvero ogni elemento è rappresentante.

Dimostrazione

Ricordiamo che $Cl(x)=\{y\in X:xRy\}$.

1° punto: Supponiamo che $Cl(x)=Cl(y)$, dato che $R$ è riflessiva si ha che $y\in Cl(y)$ e quindi per l’ipotesi abbiamo che $y\in Cl(x)$ ovvero che $x$ è in relazione con $y$ $xRy$.

Adesso supponiamo che $xRy$, allora $y\in Cl(x)$. Sia $z\in Cl(y)$ si ha che $yRz$ quindi dato che $xRy\wedge yRz$ otteniamo che $xRz$ ovvero $z\in Cl(x)$ dato che la relazione è transitiva.

Quindi $Cl(y)\subset Cl(x)$, ma dato che $R$ è simmetrica e quindi $xRy\iff yRx$ posso scambiare $x$ e $y$ e mostrare nello stesso modo che $Cl(x)\subset Cl(y)$. Quindi siccome ho dimostrato che $Cl(y)\subset Cl(x)\wedge Cl(x)\subset Cl(y)$ allora so che $Cl(x)=Cl(y)$.

2° punto: Vogliamo dimostrare che $\forall x,y\in X$ o $Cl(x)=Cl(y)$ oppure sono disgiunte ovvero $Cl(x)\cap Cl(y)=\varnothing$.

Siano $x,y\in X$ se $Cl(x)\cap Cl(y)=\varnothing$ non c’è nulla da dimostrare.

Supponiamo che $Cl(x)\cap Cl(y)\ne \varnothing$, sia $z\in Cl(x)\cap Cl(y)$ allora si ha che $xRz,yRz$ (per simmetria abbiamo che $zRy$) e quindi per transitività $xRz\wedge zRy\Rightarrow xRy$, inoltre per il punto 1 abbiamo che $Cl(x)=Cl(y)$ dato che sono in relazione.

Insieme delle Parti

Dato $X\ne \varnothing$, consideriamo un insieme $\mathcal{P}$ di sottoinsiemi di $X$, quindi $P\in \mathcal{P}\Rightarrow P\subset X$.

Quindi $\mathcal{P}(X):=\{P:P\subset X\}$ viene chiamato insieme delle parti, si ha quindi che $P\in \mathcal{P}(X)\iff P\subset X$.

Sia $\mathcal{P}\subset \mathcal{P}(X)$ non vuoto si dice che $\mathcal{P}$ è una partizione di $X$ se:

1. $\forall P\in \mathcal{P}P\ne \varnothing$
2. $\forall P,Q\in \mathcal{P}P\ne Q\Rightarrow P\cap Q\ne \varnothing$
3. $\forall x\in X\exists !P\in \mathcal{P}t.c.x\in P$

Quindi, gli insiemi non devono essere vuoti, non ci devono essere insiemi con elementi in comune e tutti i punti del dominio devono stare in un solo insieme. L’unicità nell’ultima condizione non è obbligatoria dato che sono “coperto” dalla seconda condizione.

Esempio

Partizione di $X$ in 9 parti.

$$X=\underset{i=1}{\overset{9}{⨆}}{P}_i$$

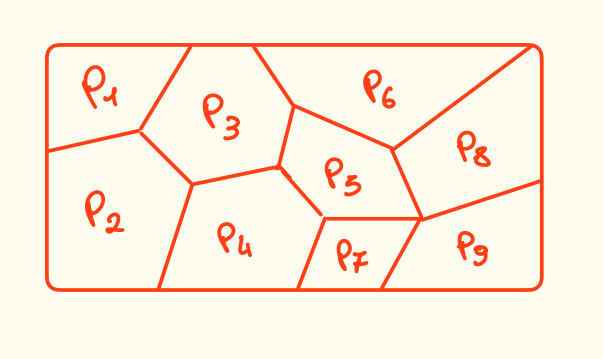
Proposizione 2

Data $R=(X,\Gamma )$ una relazione d’equivalenza, $\mathcal{P}=\{Cl(x):x\in X\}$ è una partizione di $X$.

Dimostrazione

Se $P\in \mathcal{P}$, allora $P$ è una classe di equivalenza di un elemento quindi $P=Cl(x)$ con $\exists x\in X$.

Dato che $R$ è riflessiva abbiamo che $x$ stesso appartiene alla classe di equivalenza e quindi $x\in P\Rightarrow P\ne \varnothing$ (Rispettiamo la prima condizione).

Se $Cl(x)\ne Cl(y)\Rightarrow Cl(x)\cap Cl(y)=\varnothing$ per via della preposizione precedente che ci dice che le intersezioni o sono uguali o sono disgiunte. (Rispettiamo anche la seconda condizione).

Come detto prima dato che $R$ è riflessiva abbiamo che sia $x\in X$ allora $x\in Cl(x)$. (Terza condizione).

Definizione Quoziente di $X$ per $R$

Prendiamo $X$ con relazione d’equivalenza $R$. Il quoziente di $X$ per $R$ indicato da:

$$X/R\text{ Oppure }\frac{X}{R}$$

È l’insieme delle classi di equivalenza di $X$ per $R$:

$$X/R=\{Cl(x):x\in X\}$$

Sistema completo di Rappresentanti

Dati $X$ con relazione d’equivalenza $R$, un sistema completo di rappresentanti (SCR) è un sottoinsieme $X^{\prime }\subset X$ tale che:

1. $\forall x_1^{\prime },x_2^{\prime }\in X^{\prime }$ diversi si ha che $x_1^{\prime }/R{x}_2^{\prime }\Rightarrow Cl(x_1^{\prime })\cap Cl(x_2^{\prime })=\varnothing$
2. $\forall x\in X\exists x^{\prime }\in X^{\prime }$ tale che $x\in Cl(x^{\prime })$ ($x^{\prime }$ è unico perché garantito dalla prima condizione)

Quindi un sistema completo di rappresentanti è un insieme di elementi scelti in modo che rappresentino esattamente una sola classe d’equivalenza.

Esempio 1

$X=\{r\text{ retta di }{\mathbb{R}}^2\}$, $R=||$ parallelismo, allora $R$ è una relazione d’equivalenza.

$X^{\prime }=\{\text{rette per l’origine}\}$ è un sistema completo di rappresentanti per $R=||$, infatti:

1. Due rette che passano per l’origine distinte non sono parallele, quindi nessun elemento di $X^{\prime }$ è in relazione con un altro.
2. Data una retta $r\in X$ esiste un’unica retta $r^{\prime }\in X^{\prime }$ con $r^{\prime }||r$, ovvero un’unica retta parallela ad $r$ passante per l’origine.

Osservazione

Non c’è unicità nella scelta di un SCR, questo significa che abbiamo a disposizione più scelte possibili purché rispettiamo le condizioni.

Un esempio più semplice per capire il funzionamento può essere ad esempio la divisione per 3 e i suoi resti, abbiamo 3 resti possibili:

• resto 0 dato da: {0, 3, 6, 9, 12, …}
• resto 1 dato da: {1, 4, 7, 10, 13, …}
• resto 2 dato da: {2, 5, 8, 11, 14, …}

Possiamo scegliere come SCR {0, 1, 2} ma anche {9, 4, 14} e così via, l’importante è che scegliamo un solo elemento per ogni classe d’equivalenza.

Esempio 2

1. $X\ne \varnothing$ e dati $x,x^{\prime }\in X$ si ha che $x{R}_1{x}^{\prime }\iff x=x^{\prime }$ quindi $R_1$ è l’uguaglianza. In questo modo otteniamo che $X/R_1=X$ quindi ogni classe d’equivalenza è un singleton infatti ogni elemento è uguale solo a se stesso e quindi $X$ è l’unico SCR

2. Se invece abbiamo $x,x^{\prime }\in X$ allora $x{R}_2{x}^{\prime }$ avviene sempre, in questo caso abbiamo una sola classe di equivalenza e quindi $X/R_2$ è un singleton, ogni SCR è quindi un singleton della forma $\{x\}$ con $x\in X$.

   Ovvero possiamo prendere qualsiasi elemento dell’insieme come SCP dato che sono tutti in relazione fra loro.

Applicazioni (funzioni)

Una corrispondenza $f=(A,B,\Gamma )$ con la proprietà che $\forall a\in A\exists !b\in B$ con $(a,b)\in \Gamma$ si dice applicazione e si scrive $b=f(a)$. Si scrive anche $A\stackrel{f}{\to }B$.

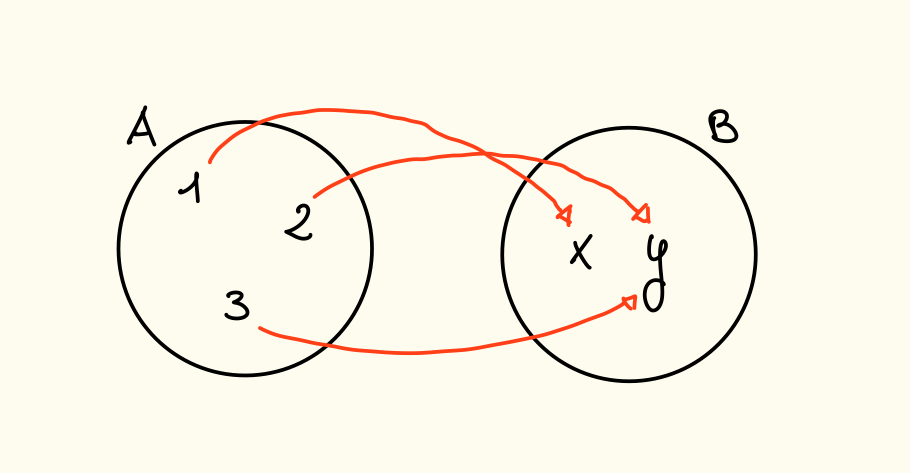
Quindi otteniamo che $\Gamma =\{(1,x),(2,y),(3,y)\}$ e ad esempio $x=f(1)$.

Il codominio si dice anche insieme immagine.

Sia $f:X\to Y$ applicazione e $X^{\prime }\subset X$ allora $f(X^{\prime }):=\{y\in Y:\exists x\in X^{\prime }\text{ con }f(x)=y\}$, questo è l’insieme immagine di $X^{\prime }$ per $f$, quindi $f(X^{\prime })\subset Y$.

Dato invece un insieme $Y^{\prime }\subset Y$, l’insieme $f^{-1}(Y^{\prime })=\{x\in X:f(x)\in Y^{\prime }\}$ è detto co-immagine o anche immagine inversa di $Y^{\prime }$, abbiamo che $f^{-1}(Y^{\prime })$ è sottoinsieme di $X$.

In poche parole l’insieme coimmagine è l’insieme delle classi di equivalenza create dalla relazione, quindi prendendo l’esempio di prima abbiamo come insieme coimmagine: $\{\{1\},\{2,3\}\}$ dato che 1 è l’unico elemento che mappa $x$ mentre 2 e 3 sono gli elementi che mappano $y$.

Se invece noi scriviamo $f^{-1}(\{y\})$ otteniamo $2,3$.

Tipi di Applicazioni

Funzioni Iniettive

È detta iniettiva se $x,x^{\prime }\in X$ e $f(x)=f(x^{\prime })$ allora $x=x^{\prime }$ oppure possiamo scrivere anche $\forall y\in Y$ abbiamo $f^{-1}(\{y\})=\varnothing \vee \text{singleton}$.

Funzioni Suriettive

Si dice che $f$ è suriettiva se $f(X)=Y$ oppure $\forall y\in Y,\exists x\in X$ tale che $f(x)=y$, quindi ogni valore del codominio deve essere raggiunto da almeno un valore del dominio.

Si può anche scrivere $\forall y\in Y,f^{-1}(\{y\})\ne \varnothing$.

Funzioni Biettive

Una funzione $f:X\to Y$ è biiettiva se è al tempo stesso suriettiva e iniettiva.

Quindi $f$ biiettva se e solo se $\forall y\in Y,f^{-1}(\{y\})$ è un singleton, ovvero ogni elemento del codominio ha un unico elemento del dominio associato. Infatti la suriettività toglie una possibilità all’esito della condizione di initetività ($\varnothing$) lasciando soltanto il caso singleton.

Operazioni sulle Funzioni

Prima di vedere le operazioni, vediamo cos’è un diagramma.

Definizione Diagramma

È una collezione di insiemi non vuoti collegati da applicazioni Esempi

Noi vedremo diagrammi del tipo:

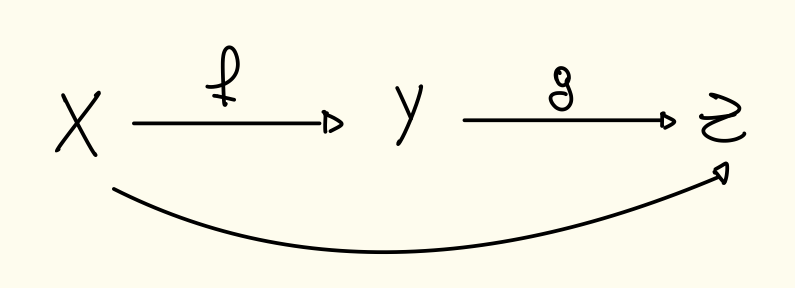
Composizione

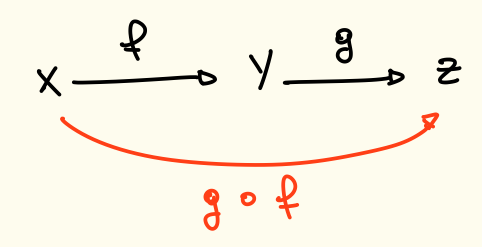
Si definisce funzione composta $X\stackrel{g\circ f}{\to }Z$.

Notazioni

Nel diagramma vediamo prima $f$ e poi $g$ ma nella funzione composta scriviamo prima $g$ e poi $f$ questo perché si calcola prima il risultato di $f$ e si “fornisce” a $g$ ovvero $g(f(x))$. Si legge “g composta f”.

Con tre funzioni:

$$X\stackrel{f}{\to }Y\stackrel{g}{\to }Z\stackrel{h}{\to }T$$

Otteniamo:

$$(h\circ g\circ f)(x)=h(g(f(x)))$$

Per le funzioni composte vale la proprietà associativa:

$$(h\circ g)\circ f=h\circ (g\circ f)$$

Proposizione

Dato il diagramma $X\rightleftarrows Y$ con $f:X\to Y$ e $g:Y\to X$.

Diciamo che $f$ è biiettiva $\iff \exists g:Y\to X,t.c.f\circ g\stackrel{②}{=}i{d}_y,g\circ f\stackrel{①}{=}i{d}_x$. Quindi $f$ è biiettiva se e solo se esiste una funzione $g$ che va da $Y$ ad $X$ tale che $f$ composta $g$ restituisca $y$ (parto da $Y$ con $g$ e ritorno in $Y$ con $f$) e tale che $g$ composta $f$ restituisca $x$ (parto da $X$ con $f$ e ritorno in $X$ con $g$).

$g$ è detta funzione inversa di $f$, se esiste è unica.

Dimostrazione

Partiamo dalla condizione che $f$ è biiettiva, allora $\forall y\in Y\exists !x\in Xt.c.f(x)=y$.

Poniamo $g(y)=x$.

Se $x\in X$, $g(f(x))=g(y)=x$ e $x$ è l’unico elemento t.c. $f(x)=y$ allora $g(x)=x\Rightarrow g\circ f=i{d}_x$ (①), analogamente possiamo ottenere $f\circ g=i{d}_y$ ovvero ②.

---

Partiamo dalla condizione a destra quindi abbiamo il diagramma $X\rightleftarrows Y$ con $f:X\to Y$ e $g:Y\to X$ e $f\circ g\stackrel{①}{=}i{d}_y$ e $g\circ f\stackrel{②}{=}i{d}_x$.

Possiamo mostrare allo stesso modo sia $f$ che $g$ suriettive e iniettive, mostriamo $g$:

Suriettiva:

Sia $x\in X$ poniamo $y=f(x)$, quindi $g(y)=g(f(x))=(g\circ f)(x)=x$ per via di ② ne deduciamo che $g^{-1}(\{x\})\ne \varnothing$ e quindi $g$ è suriettiva.

Iniettiva:

Siano $y,y^{\prime }\in Y$ t.c. $g(y)=g(y^{\prime })=x$ allora applicando $f$ ottengo:

$$\underset{\underset{\text{Per ①, = y}}{\underbrace{(f\circ g)(y)}}}{\underbrace{f(g(y))}}=\underset{\underset{\text{Per ①, = y’}}{\underbrace{(f\circ g)(y^{\prime })}}}{\underbrace{f(g(y^{\prime }))}}=\underset{y}{\underbrace{f(x)}}$$

Quindi $y=y^{\prime }$, $g$ è iniettiva.

Se $g$ è sia iniettiva che suriettiva allora è biiettiva.

Teorema Struttura Applicazioni

$X\stackrel{f}{\to }Y$, abbiamo come obiettivo quello di costruire una relazione d’equivalenza $\sim$ su $X$.

Si pone $x,x^{\prime }\in X,x\sim x^{\prime }\iff f(x)=f(x^{\prime })$ allora $\sim$ è una relazione d’equivalenza:

• $x\sim x:f(x)=f(x)$ | Riflessiva
• $x\sim x^{\prime }\iff f(x)=f(x^{\prime })\iff f(x^{\prime })=f(x)\iff x^{\prime }\sim x$ | Simmetrica
• $x\sim x^{\prime },x^{\prime }\sim x^{\prime \prime }\iff f(x)=f(x^{\prime }),f(x^{\prime })=f(x^{\prime \prime })\Rightarrow f(x)=f(x^{\prime \prime })\Rightarrow x\sim x^{\prime \prime }$ | Transitiva

Consideriamo l’insieme quoziente $X\backslash \sim$ allora:

$$X^{\prime }\in X\backslash \sim \iff X^{\prime }\subset Xe\exists y\in Y:X^{\prime }=f^{-1}(\{y\})$$

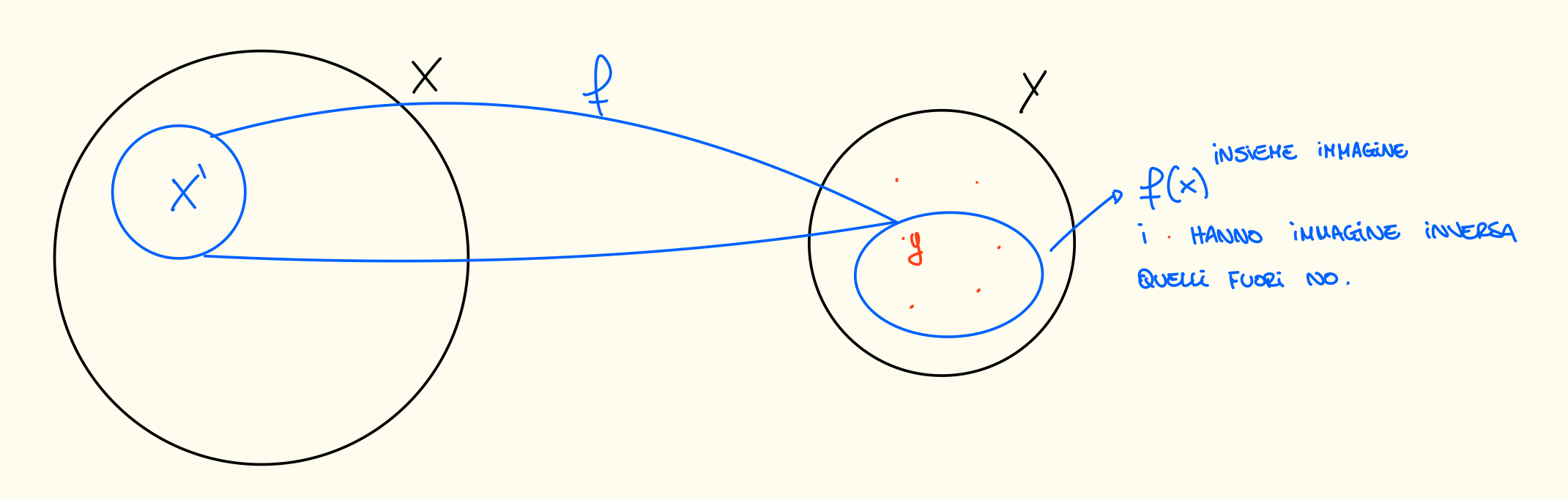
1. $\forall x\in X\exists X^{\prime }\in X\backslash \sim t.c.x\in X^{\prime }$ Ogni elemento fa parte di una classe di equivalenza.
2. $X_1^{\prime },X_2^{\prime }\in X\backslash \sim$ e $X_1^{\prime }\ne X_2^{\prime }\Rightarrow X_1^{\prime }\cap X_2^{\prime }=\varnothing$ Le classi di equivalenza non hanno elementi in comune.
3. Se $X^{\prime }\in X\backslash \sim$ allora $f{|}_{X^{\prime }}$ è costante ovvero l’immagine è un singleton, questo perché elementi di X in relazione (fanno parte di un X’) hanno la stessa immagine.

Adesso, costruiamo a partire da $X\stackrel{f}{\to }Y$ un’applicazione $\varphi =X\backslash \sim \to f(X)\subset Y$.

Sia $X^{\prime }\in X\backslash \sim$ allora $X^{\prime }=[x]\exists x\in X$.

Si pone $y=f(x)\in Y$ allora definiamo $\varphi (X^{\prime })=y$ non deve dipendere dal rappresentante (ben definita):

$$C=[x]=[x^{\prime }]f(x)=f(x^{\prime })$$

$\varphi$ è biiettiva e permette di calcolare $f$ fattorizzandola nel diagramma:

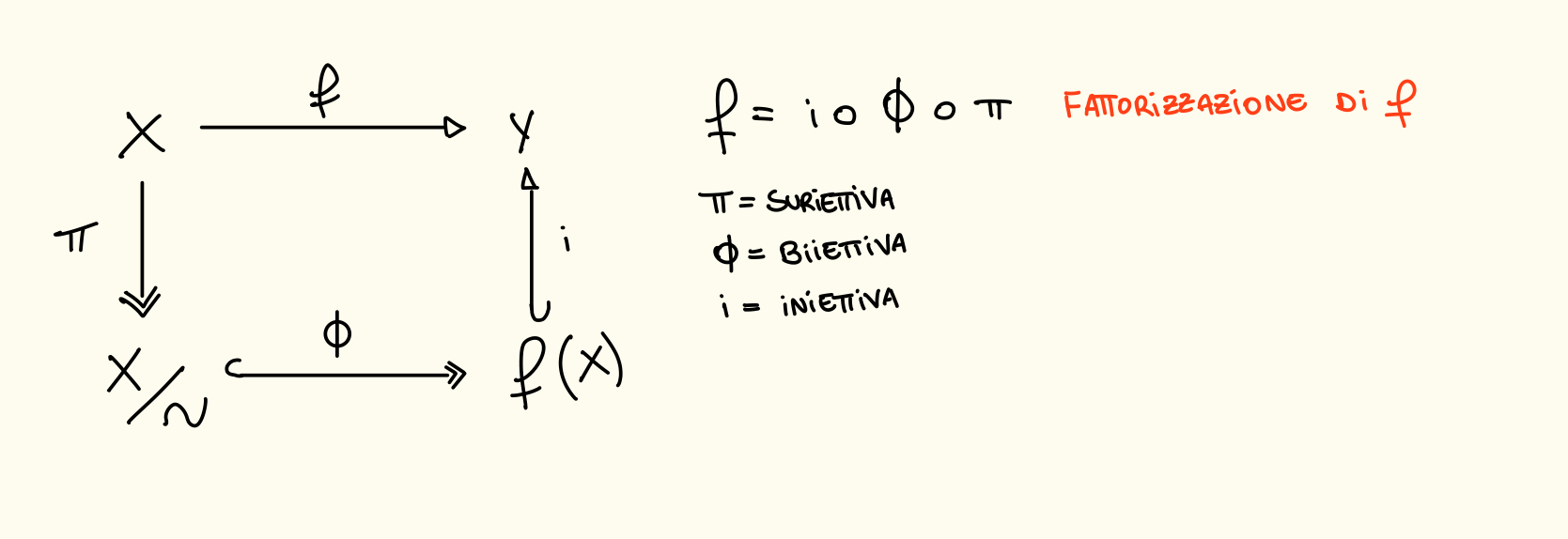
** f(x) è un sottoinsieme di Y

Biiettiva

Per vedere che $\varphi$ è biiettiva poniamo per $y\in f(X),\psi (y)=\{x\in X:f(x)=y\}$ tale insieme è $\ne \varnothing$ quindi $f$ è suriettiva nella sua immagine. $\psi (y)=[x]$ con $f(x)=y$ (dato che tutti gli elementi di $X$ in relazione hanno stessa immagine) di modo che $\psi ={\varphi }^{-1}$.

1. $\varphi$ è ben definita. Questo perché se $X^{\prime }=[x]=[x^{\prime }]$ si ha $f(x)=f(x^{\prime })=y\in f(X),f(X^{\prime })$ è un singleton di $f(X)$
2. $\varphi$ è biiettiva, ${\varphi }^{-1}(y)=f^{-1}(\{y\})\in X\backslash \sim$, $f^{-1}(\{y\})$ mi restituisce tutti gli elementi di $X$ che hanno come immagine $y$
3. $f=i\circ \varphi \circ \pi$. Poniamo $y=f(x)$ con $x\in X$. Allora $\pi (x)=f^{-1}(\{y\})$. Quindi $(\varphi \circ \pi )(x)=y$ e $(i\circ \varphi \circ \pi )(x)=y=f(x)$.

Esempio

Abbiamo $X=\mathbb{Z},b\in {\mathbb{N}}^{\ast }$ e $Y=\{0,\dots ,b-1\}$, ricordiamo che ${\mathbb{N}}^{\ast }=\mathbb{N}\backslash \{0\}$.

Algoritmo della divisione euclidea per b

$\forall x\in \underset{X}{\underbrace{\mathbb{Z}}}\exists !(q,r)\in \mathbb{Z}\times \underset{Y}{\underbrace{\{0,\dots ,b-1\}}}$ tale che $x=qb+r$ dove:

• $r$ resto
• $q$ quoziente

Stiamo dicendo quindi che per ogni numero appartenente a Z esiste una sola coppia appartenente al prodotto cartesiano fra Z e i possibili resti (da 0 a b-1). Infatti le coppie sono composte da un numero q quoziente e il resto associato.

Definiamo $f:X\to Y$ ponendo $f(x):=r$. Questa è ben definita e si chiama riduzione modulo b, è un’applicazione suriettiva: $f(X)=Y$. Ad esempio se $b=2$ allora $f(5)=1,f(4)=0$.

Allora la relazione d’equivalenza associata, che scriviamo come $\equiv$ e la chiamiamo congruenza modulo b.

Se due interi $x,x^{\prime }$ sono in relazione allora si scrive $x\equiv x^{\prime }(modb)$ e si legge x congruente a x’ modulo b.

$$X^{\prime }\in X\backslash \equiv \iff \exists r\in Y,\forall x\in X^{\prime },x=qb+r$$

Quindi tutte le $x$ di $X^{\prime }$ devono avere lo stesso resto. Inoltre l’insieme $Y\subset \mathbb{Z}$ è in questo caso un SCR dato che:

1. $f$ suriettiva e quindi $\forall r\in Y,\exists x\in X$ t.c. $x\equiv r(modb)$
2. Presi $r,r^{\prime }\in Y$ con $r\ne r^{\prime }$ si ha che $r\not\equiv r^{\prime }(modb)$ infatti supponiamo per assurdo che $r\equiv r^{\prime }(modb)$:

$$\{\begin{array}{l}r=qb+\tilde{r}\\ r^{\prime }=q^{\prime }b+\tilde{r}\end{array}$$

Quindi $r-r^{\prime }=(q-q^{\prime })\cdot b$

$r-r^{\prime }=b\cdot k(\underset{\text{percheˊ }r\ne r^{\prime }}{\underbrace{k\in \mathbb{Z}\backslash \{0\}}}),k>0\Rightarrow r=r^{\prime }+bk\ge r^{\prime }+b$ ma $r\ge r^{\prime }+b\ge b$ è una contraddizione dato che i resti vanno da 0 a $b-1$.

$\varphi$ è la biiezione tra $X\backslash \equiv$ e $Y$ che manda ogni classe $X^{\prime }$ nell’unico $r\in Y$ t.c. $\forall x\in X^{\prime },f(x)=r$, in pratica $r$ è il resto in $Y$ della divisione euclidea di $x$ per $b$ e non cambia al variare di $x$ in $X^{\prime }$, ovvero tutti gli elementi presenti in $X^{\prime }$ hanno lo stesso resto.

$$\forall X^{\prime }\in X\backslash \equiv \text{ si scrive }{X}^{\prime }=\overline{x}=\overline{x^{\prime }}=\overline{r}\forall x,x^{\prime }\in X$$

e se

$$\varphi (X^{\prime })=r\in Y=f(X)=f(Y)$$

Congettura di Collatz

Spiegato a lezione non so di preciso perché, però è simpatico wikipedia

Esercizio

Studiare l’applicazione $f:\mathbb{Z}\to \mathbb{Z}$ che ad $x\in \mathbb{Z}$ associa $f(x)=ax+1$. Al variare del parametro $a\in \mathbb{Z}$ dire quando la funzione è suriettiva e iniettiva.

• Se $a=0$ allora $\forall x\in \mathbb{Z}$ abbiamo che $f(x)=1$ e quindi $f$ non è ne iniettiva ne suriettiva, infatti a $x$ diverse abbiamo immagini uguali (iniettività) e non tutto il codominio ha controimmagine (suriettività).

• Se $a=1$, otteniamo che $f(x)=x+1$, ha anche una formula inversa $g(y)=y-1$ ed è quindi biiettiva, infatti:

$(f\circ g)(y)=f(y-1)=(y-1)+1=y\Rightarrow f\circ g=I{d}_{\mathbb{Z}}$ e,

$(g\circ f)(x)=g(x+1)=(x+1)-1=x\Rightarrow g\circ f=I{d}_{\mathbb{Z}}$

• Se $a=-1$ con ragionamenti analoghi troviamo lo stesso risultato ovvero che $f$ è biiettiva

• Se $a\notin \{0\}$ allora $f$ è iniettiva, infatti: $f(n_1)=f(n_2)\iff a{n}_1+1=a{n}_2+1\iff \underset{\text{Ricordiamo che a non puoˋ essere nullo}}{\underbrace{a(n_1-n_2)=0\iff n_1-n_2=0}}\iff n_1=n_2$

• Se $a\notin \{-1,0,1\}$ $f$ non è suriettiva, infatti:

$f^{-1}(\{a\})=\varnothing$ infatti qualsiasi valore prendo per $a$ è impossibile che io copra tutto il codominio o comunque è impossibile che ci trovo $a$ stesso.

Infatti se $f$ fosse suriettiva avremmo $\exists x\in \mathbb{Z}t.c.f(x)=a$ e quindi $f(x)=ax+1=a$ che per risolverla $a(x-1)=-1\to a(1-x)=1$.

Per risolvere questa equazione in $\mathbb{Z}$ abbiamo solo due casi o $1\cdot 1$ oppure $-1\cdot (-1)$ e questo implica che $a\in \{-1,1\}$ ovvero un’ipotesi che abbiamo escluso all’inizio.

Esercizio preparazione al 21

Sia $\mathcal{P}=\{X_1,X_2\}$ una partizione di $X\ne \varnothing$ e $\mathcal{Q}=\{Y_1,Y_2,Y_3\}$ una partizione di $Y\ne \varnothing$. Graficamente abbiamo una situazione come questa:

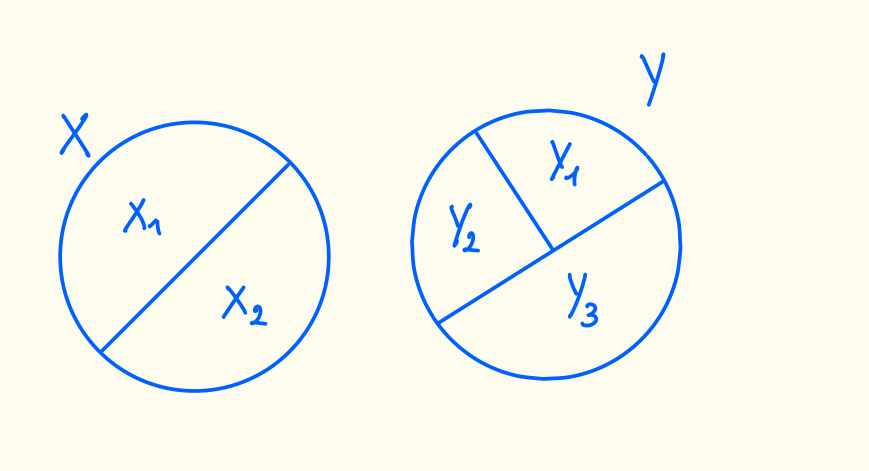
Quindi per la definizione di partizione abbiamo che $X$ ha sicuramente 2 elementi e $Y$ ne ha sicuramente 3.

Obiettivo: Mostrare che $\mathcal{R}=\{X_i\times Y_j:i=1,2;j=1,2,3\}$ è una partizione di $X\times Y$.

Proviamo prima di tutto a rappresentare in modo grafico cosa vogliamo dimostrare:

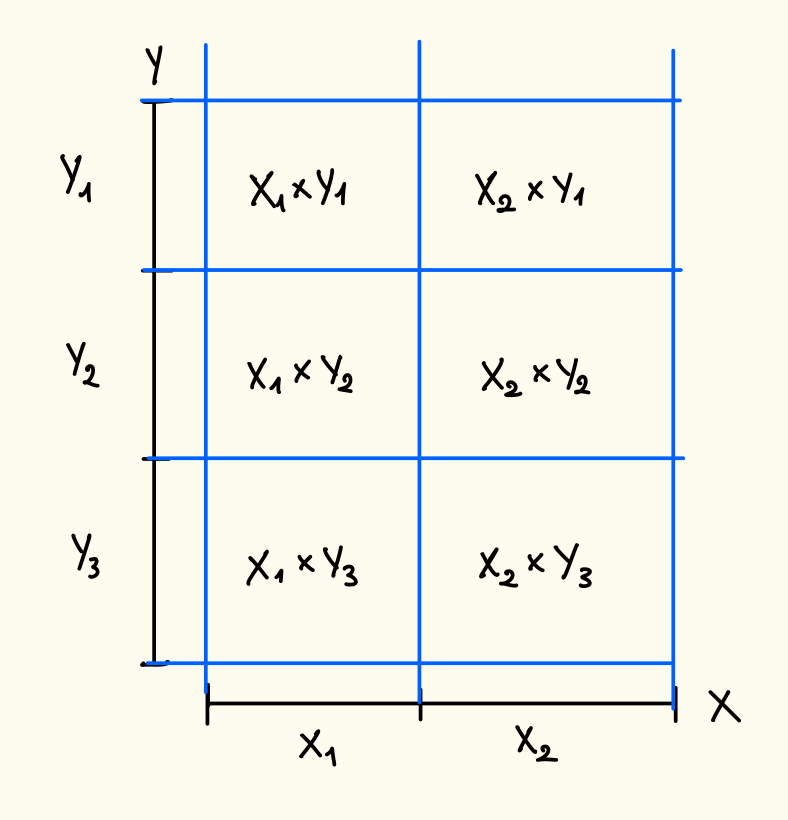
Notiamo quindi che effettivamente è una partizione, adesso dobbiamo scriverlo in linguaggio matematico.

Nel nostro caso possiamo scrivere che $X=\underset{i\in \{1,2\}}{⨆}{X}_i$ e $Y=\underset{i\in \{1,2,3\}}{⨆}{Y}_i$ con $\{X_1,X_2,Y_1,Y_2,Y_3\}\cap \{\varnothing \}=\varnothing$, ovvero dove nessun di questi insiemi è vuoto, inoltre poniamo $I=\{1,2\},J=\{1,2,3\}$.

Allora $\mathcal{R}=\{X^{\prime }\times Y^{\prime }:X^{\prime }\in \mathcal{P},Y^{\prime }\in \mathcal{Q}\}$=$\{X_1\times Y_1,X_2\times Y_1,X_1\times Y_2,X_2\times Y_2,X_3\times Y_1,X_3\times Y_2\}$.

Dobbiamo quindi dimostrare 3 punti:

1. $\forall (i,j)\in I\times J,X_i\times X_j\ne \varnothing$

   Ovvero nessuna partizione deve essere vuota, per dimostrare questo sappiamo che $X_i$ ed $Y_j$ sono partizioni rispettivamente di $\mathcal{P}$ e $\mathcal{Q}$ quindi non possono essere vuote e questo significa che non lo è nemmeno il loro prodotto cartesiano, possiamo quindi dire $(x,y)\in X_i\times Y_j\Rightarrow X_i\times Y_j\ne \varnothing$.

---

2. $\forall (x,y)\in X\times Y\exists (i,j)t.c.(x,y)\in X_i\times Y_j$

   Quindi che ogni elemento del prodotto cartesiano è all’interno di una partizione.

   Dati $(x,y)\in X\times Y$ dato che $\mathcal{P}$ è una partizione allora l’elemento $x$ farà sicuramente parte di una partizione di $X$: $x\in X_i\exists i\in I$, inoltre per lo stesso ragionamento dato che $\mathcal{Q}$ è una partizione allora anche $y$ farà sicuramente parte di una partizione di $Y:y\in Y_j\exists j\in J$.

   Mettendo insieme le conclusioni possiamo dire che $(x,y)\in X_i\times Y_j$, ovvero che qualsiasi coppia $(x,y)$ del prodotto cartesiano farà sicuramente parte di una partizione.

---

3. Se $(i,j)\ne (i^{\prime },j^{\prime })$ allora $X_i\times Y_j\cap X_{i^{\prime }}\times Y_{j^{\prime }}=\varnothing$

   Questo significa che due partizioni diverse non hanno elementi in comune.

   $(i,j)\ne (i^{\prime },j^{\prime })\iff i\ne i^{\prime }\text{ oppure }j\ne j^{\prime }$, vediamo entrambi i casi:

   Se $i\ne i^{\prime }$ allora $X_i\cap X_{i^{\prime }}=\varnothing$ dato che $\mathcal{P}$ è una partizione

   Calcoliamo allora $(X_i\times Y_j)\cap (X_{i^{\prime }}\times Y_{j^{\prime }})$=

   $$\{(x,y):x\in \underset{=\varnothing }{\underbrace{X_i\cap X_{i^{\prime }}}};y\in Y_j\cap Y_{j^{\prime }}\}=\varnothing$$

   Se invece $j\ne j^{\prime }$ allora $Y_j\cap Y_{j^{\prime }}=\varnothing$ e questo, per lo stesso ragionamento visto prima implica che $(X_i\times Y_j)\cap (X_{i^{\prime }}\times Y_{j^{\prime }})=\varnothing$.

Esercizio 12

Sia $f:\{1,\dots ,n\}\to \{1,\dots ,m\}$ un’applicazione. Si provi che se $n>m$ allora $f$ non è iniettiva e se $n>m$ allora $f$ non è suriettiva.

Iniziamo rappresentando graficamente il nostro problema per avere più chiarezza.

In questo caso $n>m$ è impossibile che $f$ sia iniettiva dato che tutti gli elementi del dominio devono avere un’immagine nel codominio.

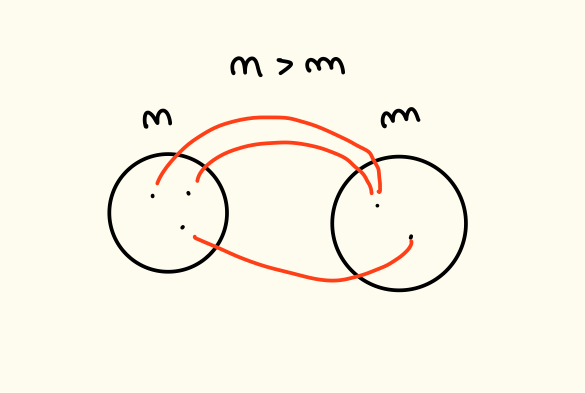
In questo caso invece $m>n$ e non possiamo avere $f$ suriettiva dato che un elemento del dominio può avere una sola immagine nel codominio e quindi alcuni elementi del codominio rimangono “scoperti” cioè senza controimmagine.

---

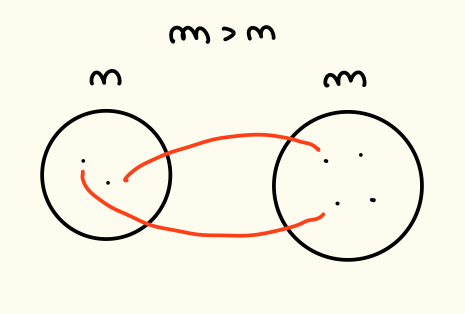
Iniziamo mostrando che se $n>m\ge 1$ allora $f$ non è iniettiva $\forall f$ applicazione.

Definiamo $E_n=\{1,\dots ,n\}$, abbiamo bisogno delle seguenti proprietà:

1. $E_n=E_{n-1}⨆\{n\}$.
2. $\forall m_0\in E_m,\exists E_m\backslash \{m_0\}\underset{\cong }{\stackrel{f}{\to }}{E}_{m-1}$
3. Sia $X\stackrel{h}{\to }Y$ iniettiva allora il grafo $\Gamma$ di $h$ ha le proprietà che $\forall y\in Y,\text{ se }\exists x\in X\text{ con }(x,y)\in \Gamma$ allora $x$ è unico.

Quindi:

1. Per questa proprietà non abbiamo nulla da dimostrare infatti dato un insieme del tipo definito prima $E_n$ questo possiamo scriverlo come l’unione fra se stesso meno un elemento e l’insieme che contiene l’elemento mancante.

2. L’applicazione $E_m\backslash \{m_0\}\stackrel{f}{\to }{E}_{m-1}$ definita da:

$$f(x)=\{\begin{array}{l}x\text{ se }x<m_0\\ x-1\text{ se }x>m_0\end{array}$$

è invertibile, infatti:

$$f^{-1}(y)=\{\begin{array}{l}y\text{ se }y<m_0\\ \\ y+1\text{ se }y\ge m_0\end{array}$$

Esempi

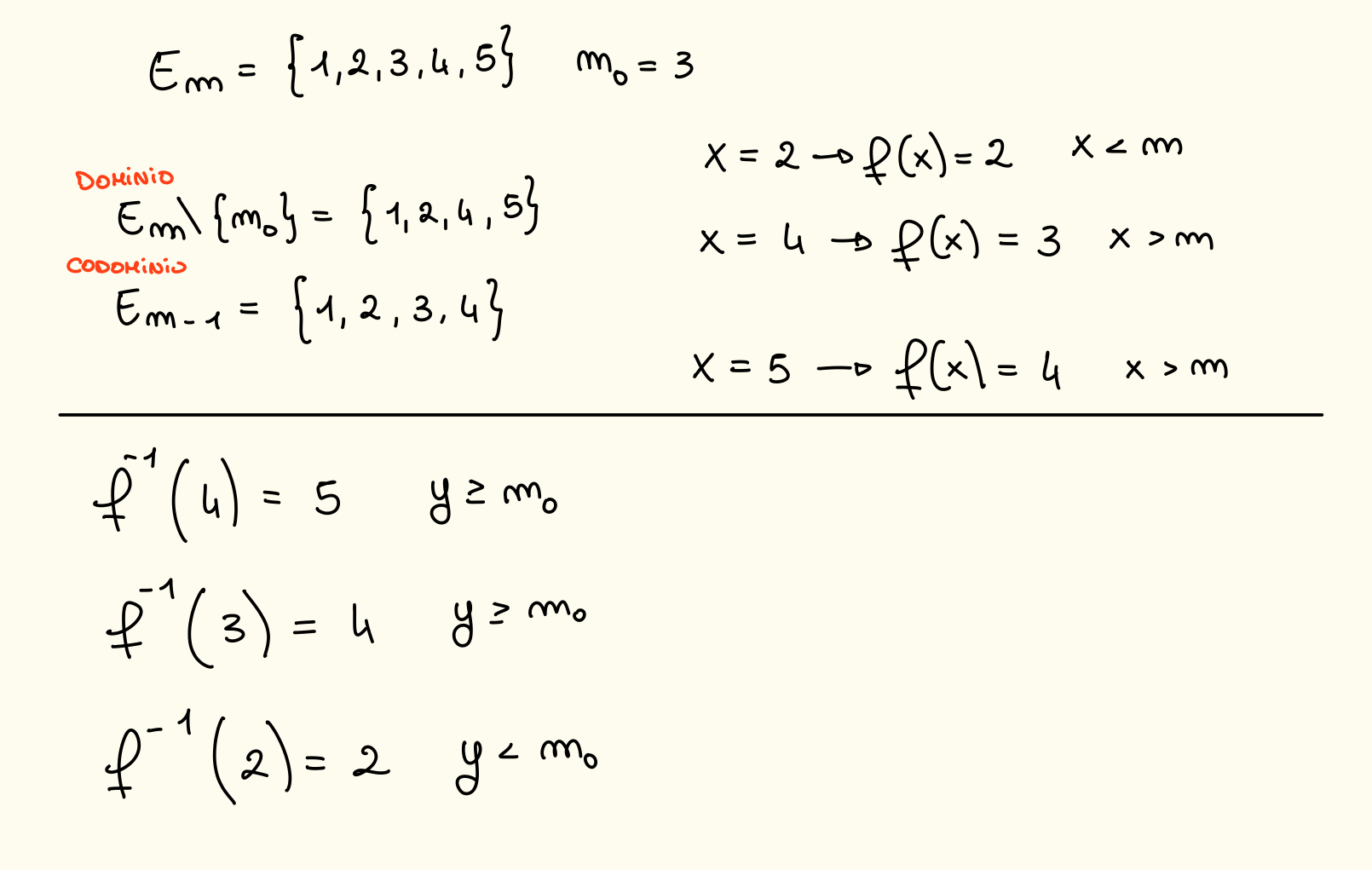
Quindi esiste una funzione biiettiva definita come prima.

3. Abbiamo $h$ iniettiva $\iff \forall y\in Y,h^{-1}(y)=\varnothing \text{ oppure singleton}$. Si ha che $\exists x\in Xt.c.h(x)=y\iff h^{-1}(y)\ne \varnothing$ dato che nel grafo $\Gamma$ ci sono solo $(x,y)t.c.\exists x\in X$ quindi la possibilità del vuoto è esclusa e quindi $x$ è sicuramente unico.

   Allora in questo caso $(x,y)\in \Gamma \iff f(x)=y\iff \{x\}=f^{-1}(y)$.

---

Adesso usiamo queste 3 proprietà per dimostrare il punto principale dell’esercizio.

Se $m=1$ non ho nulla da dimostrare, infatti sto prendendo come dominio un insieme da almeno due elementi $(n>m)$ e come codominio un insieme con un solo elemento, l’applicazione non può essere iniettiva dato che tutti gli elementi hanno come immagine lo stesso elemento (Come abbiamo mostrato con il disegno sopra).

Adesso per dimostrarlo in generale, supponiamo per assurdo che l’enunciato sia falso.

Allora $\exists n_o,m\text{ con }{n}_0>m>1eg:E_{n_0}\to E_m$ iniettiva, questi $n_0$ li possiamo “collezionare” e quindi ne esiste uno che è il più piccolo possibile, focalizziamoci su questo elemento, dato che la nostra ipotesi dovrebbe funzionare sempre.

Quindi adesso consideriamo $n_0$ come l’elemento più piccolo possibile adesso possiamo porre $m_0:=g(n_0)\in E_m$

Allora per la seconda proprietà sappiamo che $\exists E_m\backslash \{m_0\}\underset{\cong }{\stackrel{f}{\to }}{E}_{m-1}$, quindi abbiamo $g$ iniettiva e $f$ biiettiva.

Adesso dato che $n_0>m$ allora $n_0-1>m-1$ e dato che $m>1$ possiamo supporre $m\ge 1$, allora:

$$E_{n_0-1}\underset{g^{\prime }=f\circ g{|}_{E_{n_0-1}}}{\underbrace{\stackrel{g{|}_{E_{n_0-1}}}{\to }{E}_m\backslash \{m_0\}\stackrel{f}{\to }}}{E}_{m-1}$$

$g^{\prime }$ non è iniettiva perché va da $E_{n_0-1}$ a $E_{m-1}$, e noi avevamo affermato che $n_0$ era il più piccolo valore per cui esisteva una funzione iniettiva.

---

Per la proprietà 3 sappiamo che sia ${\Gamma }^{\prime }$ il grafo di $g^{\prime }$ e $g^{\prime }$ non è iniettiva allora $\exists y\in Y=E_{m-1}$ e $x_1,x_2\in X=E_{n_0-1}{x}_1\ne x_{2}t.c.(x_1,y),(x_2,y)\in {\Gamma }^{\prime }$, ovvero che esistono due valori del dominio diversi tali che hanno la stessa immagine.

Questo implica che $g{|}_{E_{n_0-1}}$ non è iniettiva.

Da capire meglio:

Infatti $(x_1,f^{-1}(y)),(x_2,f^{-1}(y))$ appartengono al suo grafo $\tilde{\Gamma }$ , ma il grafo $\Gamma$ di $g$ è dato da $\tilde{\Gamma }⨆\{(n_0,m_0)\}$ che contiene sempre i due elementi visti prima, per cui $g$ non è iniettiva → contraddizione.

Anelli

Possiamo prendere come esempio di anello l’insieme dei numeri relativi $\mathbb{Z}$.

Definizione Anello

Un anello commutativo unitario è una sestupla del tipo $(A,+,-,\cdot ,0_A,1_A)$.

Prendendo come esempio $\mathbb{Z}$ abbiamo che:

• $A$ è un insieme $\ne \varnothing$
• $+,\cdot$ sono applicazioni $A\times A\to A$ dette somma e moltiplicazione
• $-$ è un’applicazione $A\to A$, e si chiama opposto; abbiamo che $a+(-a)=0$
• $0_A$ è l’elemento neutro per l’operazione $+$
• $1_A$ è l’elemento neutro per l’operazione $\cdot$

Nel caso della moltiplicazione abbiamo che:

$$a\cdot b=\{\begin{array}{l}\text{se }b=0{\to }_0\\ \text{se }b>0\to \underset{b\text{ volte}}{\underbrace{a+\cdots +a}}\\ \text{se }b<0\to (-a)\cdot (-b)\text{ che eˋ ben definita dall’opposto}\end{array}$$

Deve soddisfare varie proprietà e le dividiamo in due categorie:

1. Proprietà Commutativa per la Somma: $\forall a,b\in A,a+b=b+a$
2. Associatività dell’addizione: $\forall a,b,c\in A,(a+b)+c=a+(b+c)$
3. Elemento Neutro addizione: $\exists 0_A\in At.c.\forall a\in A,a+0_A=0_A+a=a$
4. Elementro Opposto: $\forall a\in A\exists (-a)t.c.a+(-a)=0_A$

Queste 4 proprietà ci spiegano che $(A,+,-,0_A)$ è un gruppo commutativo abeliano.

5. Commutatività moltiplicazione: $\forall a,b\in Aa\cdot b=b\cdot a$, grazie a questa si dice che l’anello è commutativo
6. Associtatività moltiplicazione: $\forall a,b,c\in A(a\cdot b)\cdot c=a\cdot (b\cdot c)$, A è associativo
7. Elemento neutro moltiplicazione: $\exists 1_A\in At.c.\forall a\in A,a\cdot 1_A=1_A\cdot a=a$, si dice che A è unitario
8. Proprietà distributiva: $\forall a,b,c\in A,a\cdot (b+c)=a\cdot b+a\cdot c$

$(\mathbb{Z},+,\cdot )$ è un anello commutativo unitario. Questo perché l’addizione lo è sempre, quindi dobbiamo guardare se valgono le operazioni per la moltiplicazione.

Elementi Neutri

Se gli elementi neutri di moltiplicazione e addizione coincidono allora l’anello è un singleton 0. Se $1_A=0_A$ allora $A=\{0\}$.

Esistono anche altre due proprietà che valgono per $\mathbb{Z}$:

Proprietà di Tricotomia:

Esiste un sottoinsieme ${\mathbb{N}}^{\ast }\subset \mathbb{Z}$ che permette di definire una relazione su $\mathbb{Z}$:

$$a>b\iff a-b\in {\mathbb{N}}^{\ast }$$

Infatti:

$$\forall a\in \mathbb{Z}\text{ si ha }\{\begin{array}{l}a\in N^{\ast }\text{ oppure}\\ a=0\text{ oppure }\\ -a\in {\mathbb{N}}^{\ast }\end{array}$$

Quindi: Un intero può essere soltanto positivo, negativo o nullo.

Assioma di buon ordinamento:

Ogni sottoinsieme $E\subset {\mathbb{N}}^{\ast }$ non vuoto possiede un più piccolo elemento che per $<\text{ vale la proposizione }\exists c\in Et.c.\forall e\in E\backslash \{c\}$ si ha $e>c$.

Un anello che rispetta buon ordinamento e triconomia è “essenzialmente $\mathbb{Z}$“.

Se $a<b,c<d$ allora $a+c<b+d$ e $-a>-b$, le operazioni $+,>$ sono compatibili e in modo simile c’è compatibilità anche tra $\cdot ,>$.

Legge di Cancellazione in $\mathbb{Z}$:

Se $ab=ac$ con $a\ne 0$ allora $b=c$ infatti si può supporre che $a>0$, nel caso $a=1$ è chiaro mentre prendiamo $(a-1)$ e vediamo per induzione:

$$\begin{array}{rl}& (a-1)\cdot b=(a-1)\cdot c\\ & \text{Se }b\ne c\text{ e }b>c\Rightarrow (a-1)\cdot b+b>(a-1)\cdot c+c\\ & \text{E questo significa che }\underset{ab}{\underbrace{(a-1+1)\cdot b}}>\underset{ac}{\underbrace{(a-1+1)\cdot c}}\end{array}$$

Abbiamo aggiunto $+b,+c$ anche se valori diversi per l’ipotesi perché abbiamo portato l’espressione da $=$ a $>$ e dato che abbiamo detto $b>c$ questo non altera il valore dell’espressione.

Dato che avevamo supposto $ab=ac$ ma abbiamo ottenuto una contraddizione ovvero $ab>ac$ con $b\ne c$, per tricotomia deve essere necessariamente vero che $b=c$.

Elementi Invertivibili:

$A$ è un anello commutativo unitario dove $1_A\ne 0_A$.

Definizione

$a\in At.c.\exists b\in A:ab=ba=1_A$, è detto elemento invertibile (si dice che $b$ è l’inverso di $a$ e si scrive $b=a^{-1}$)

Esempio

$1_A$ è invertibile con inverso $1_A^{-1}=1_A$

Esercizio

Se $a$ è invertibile allora $a^{-1}$ è unicamente determinato.

$$\begin{array}{rl}& a\cdot b=a\cdot b^{\prime }=1\text{ con }b,b^{\prime }\in A\\ & \text{allora}\\ & (a\cdot b)\cdot b^{\prime }=1_A\cdot b^{\prime }=b^{\prime }e(a\cdot b^{\prime })\cdot b=1_A\cdot b=b\\ & \\ & \underset{(a\cdot b)\cdot b^{\prime }}{\underbrace{(a\cdot b)\cdot b^{\prime }}}=a(b\cdot b^{\prime })\underset{=}{\underbrace{=}}a\cdot (b^{\prime }\cdot b)=\underset{(a\cdot b^{\prime })\cdot b}{\underbrace{(a\cdot b^{\prime })\cdot b}}\end{array}$$

Quindi abbiamo ottenuto che le due proposizioni iniziali sono uguali e quindi $b=b^{\prime }$ e l’inverso $a^{-1}$ di $a$ è ben determinato.

Altri Esempi

$A$ è sempre anello.

---

$\forall a\in A,a\cdot 0_A=0_A$

Allora

$$\begin{array}{rl}a\cdot 0_A=a\cdot (0_A+(-0_A))=a\cdot 0_A+a\cdot (-0_A)& =a\cdot 0_A+(-a)\cdot 0_A\\ & =a\cdot 0_A+(-a\cdot 0_A)\\ & =\underset{\text{Somma fra opposti}}{\underbrace{a\cdot 0_A+(-(a\cdot 0_A))}}=0_A\end{array}$$

---

Supponiamo che $0_A=1_A$ mostriamo che $\forall a\in A$ si ha che $a=0_A$ ovvero $A=\{0_A\}$.

$$a\in A:1_A=0_A\Rightarrow \underset{a}{\underbrace{a\cdot 1_A}}=a\cdot 0_A\stackrel{(1)}{=}{0}_A\text{ Quindi }\forall a\in A:a=0_A$$

---

Se $1_A\ne 0_A$ allora $0_A\notin A^X$ (non invertibile). Infatti supponiamo per assurdo che sia invertibile allora $\exists x\in A^{X}t.c{1}_A=x\cdot 0_A\text{ Ma sappiamo che eˋ}\stackrel{(1)}{=}{0}_A$ ed è quindi una contraddizione.

Nota:

Si pone $A^X=\{a\in At.c.\text{a eˋ invertibile}\}$.

Elementi neutri pt2

Anello con $0_A\ne 1_A$ significa che $0_A$ non è invertibile, questa proprietà infatti vale solo in anelli $=\{0\}$ ovvero quando $0_A=1_A$.

Esercizio - Unico elemento neutro ad ogni anello commutativo unitario

Siano $u,u^{\prime }$ due elementi neutri quindi significa che $\forall a\in A$ otteniamo:

$$au=ua=aea{u}^{\prime }=u^{\prime }a=a$$

Se prendiamo $a=u$? Otteniamo $u{u}^{\prime }=u^{\prime }u=u$

Se prendiamo $a=u^{\prime }$? Otteniamo $u^{\prime }u=u{u}^{\prime }=u^{\prime }$

Quindi notiamo che $u=u^{\prime }$ e quindi l’elemento neutro per la moltiplicazione è unicamente determinato.

Relazione di Divisibilità

Introduciamo la relazione che dati $a,b\in A$ $a|b\iff \exists c\in At.c.b=a\cdot c$, ovvero ”$a$ divide $b$” se e solo se esiste un certo $c$ in $A$ tale che possiamo scrivere $b=a\cdot c$. Ad esempio $2|6$ infatti $6=2\cdot 3$

Innanzitutto notiamo che questa è una relazione riflessiva infatti $\forall a\in A,a=a\cdot 1_A$ ovvero $a$ divide sempre $a$.

Inoltre è anche transitiva infatti supponiamo di avere $a,b,c\in A$ e supponiamo che $a|b$ e $b|c$:

$$\begin{array}{rl}& a|b\iff b=a\cdot a^{\prime }\exists a^{\prime }\in A\\ & b|c\iff c=b\cdot b^{\prime }\exists b^{\prime }\in A\\ & \text{Facendo una sostituzione notiamo che}\\ & c=a\cdot \underset{a^{\prime \prime }}{\underbrace{(a^{\prime }\cdot b^{\prime })}}=a\cdot a^{\prime \prime }\end{array}$$

Abbiamo mostrato che anche $c$ quindi è divisibile per $a$, infatti possiamo scriverlo come $a$ moltiplicato per un altro valore $a^{\prime \prime }$ e quindi $a|c$.

Non è simmetrica né antisimmetrica.

Altre proprietà della divisibilità

Se $a|b$ e $a|c$ allora $a|b+c$ (compatibilità con l’addizione), vediamo perché:

$$\begin{array}{rl}& a|b\iff \exists a^{\prime }\in A\text{ t.c. }b=a{a}^{\prime }\\ & a|c\iff \exists a^{\prime \prime }\in A\text{ t.c. }c=a{a}^{\prime \prime }\\ & \\ & \text{Quindi}\\ & b+c=a{a}^{\prime }+a{a}^{\prime \prime }=a\underset{a^{\prime \prime \prime }}{\underbrace{(a^{\prime }+a^{\prime \prime })}}=a{a}^{\prime \prime \prime }\iff a|b+c\end{array}$$

Più generalmente se $\alpha ,\beta \in A$ e $a|b,a|c\iff a|\alpha b+\beta c$. Infatti facendo sempre lo stesso ragionamento di prima otteniamo tramite le sostituzioni otteniamo che:

$$\alpha b+\beta c=\alpha a{a}^{\prime }+\beta a{a}^{\prime \prime }=a\underset{a^{\prime \prime \prime }}{\underbrace{(\alpha a^{\prime }+\beta a^{\prime \prime })}}=a{a}^{\prime \prime \prime }$$

E quindi, come prima, $a|\alpha b+\beta c$.

---

In $\mathbb{Z}$ la relazione di divisibilità è “quasi antisimmetrica”, ovvero:

$$\begin{array}{rl}& \text{Prendiamo }a,b\in \mathbb{Z}\text{ t.c. }a|b\text{ e }b|a\\ & a|b\text{ e }b|a\stackrel{?}{\Rightarrow }\exists c\in {\mathbb{Z}}^X\text{ t.c. }a=bc(\text{Ovvero }a\in \{b,-b\}\text{ oppure }\{a,-a\}=\{b,-b\})\\ & \\ & (\text{nota dopo})\text{Possiamo supporre che }a,b\ne 0\text{ e quindi:}\\ & a|b,b|a\iff b=a{a}^{\prime },a=b{b}^{\prime }\exists a^{\prime },b^{\prime }\in \mathbb{Z}\\ & \\ & \text{Adesso facendo le sostituzioni:}\\ & \cancel{b}=\cancel{b}{b}^{\prime }{a}^{\prime }\Rightarrow 1=a^{\prime }{b}^{\prime }\underset{\text{Questo percheˋ a’,b’ sono invertibili}}{\underbrace{\Rightarrow a^{\prime }{b}^{\prime }\in \{1,-1\}}}\\ & \\ & \text{Questo significa che i due numeri devono essere o uguali o opposti, dato che }{a}^{\prime }{b}^{\prime }\in \{1,-1\}\end{array}$$

Nota, possiamo supporre che i due numeri sono non nulli, questo perché 0 non divide mai un altro elemento non nullo e quindi se uno dei due fosse 0, questo significa che lo sarebbe anche l’altro.

Elementi Irriducibili e Primi

Numero irriducibile

Definizione: $a\in A\backslash A^X$ con $a\ne 0$, questo è detto irriducibile se $\forall b,c\in A$ con $a=bc$ allora si che o $b\in A^X$ oppure $c\in A^X$ .

Esempi con $A=\mathbb{Z}$, ricordiamo inoltre che ${\mathbb{Z}}^X=\{-1,1\}$

$$\begin{array}{rl}& 12=4\cdot 3\text{ ma }4,3\notin {\mathbb{Z}}^X\Rightarrow \text{12 non eˋ irriducibile}\\ & 7=1\cdot 71\in {\mathbb{Z}}^X\Rightarrow \text{7 eˋ irriducibile}\\ & 9=3\cdot 3\Rightarrow \text{Non eˋ irriducibile}\end{array}$$

Numero Primo

Definizione: $a\in A\backslash A^X$ con $a\ne 0$ è detto primo se $\forall b,c\in A$ se $a|bc$ allora $a|b$ oppure $a|c$.

Supponiamo che $A=\mathbb{Z}$

Lemma: $p\in \mathbb{Z}$ primo allora $p$ è irriducibile, quindi primo $\Rightarrow$ irriducibile

Dimostrazione

Scegliamo $p$ primo, siano $a,b\in \mathbb{Z}t.c.p=a\cdot b$, per dimostrare che è irriducibile dobbiamo quindi dimostrare che o $a$ o $b$ sono uguali a 1 o -1.

$$\begin{array}{rl}& p=a\cdot b\Rightarrow p|a\cdot b\Rightarrow \underset{p\text{ eˋ primo}}{\underbrace{\text{o }p|a\text{ o }p|b}}\\ & \text{Prendiamo il primo caso, quindi supponiamo che }p|a:\\ & p|a\Rightarrow a=p\cdot a^{\prime }\exists a^{\prime }\in \mathbb{Z}\\ & \\ & \text{Se adesso sostituiamo con la condizione iniziale }p=a\cdot b:\\ & \cancel{p}=\cancel{p}\cdot a^{\prime }\cdot b\Rightarrow 1=a^{\prime }\cdot b\Rightarrow a^{\prime },b\in \{1,-1\}={\mathbb{Z}}^X\\ & \\ & \text{Quindi:}\\ & \text{Se }{a}^{\prime }=1\text{ allora }a=p\Rightarrow p=pb\Rightarrow b=1\\ & \text{Se }{a}^{\prime }=-1\text{ allora }a=-p\Rightarrow p=-pb\Rightarrow b=-1\\ & \\ & \text{Quindi in entrambi i casi almeno un fattore eˋ uguale a 1 o -1}\\ & \text{Quindi p eˋ irriducibile}\end{array}$$

Valore Assoluto

È un’applicazione che si denota $\mathbb{Z}\to \mathbb{N}$, prendiamo un $a\in \mathbb{Z}$:

$$\begin{array}{rl}& \text{Se }a=0\text{ allora }|a|=0\\ & \text{Se }a\ne 0\text{ allora }|a|=\text{L’unico elemento di }\mathbb{N}\text{ contenuto in }\{a,-a\}\end{array}$$

Teorema algoritmo divisione euclidea

Prendiamo $a,n\in \mathbb{Z}$ con $n\ne 0$ allora esistono unicamente determinati $q\in \mathbb{Z}$ ed $r\in \{0,\dots ,|n|-1\}$ tali che $a=nq+r$, dove $n$ è il quoziente e $r$ il resto.

Non facciamo dimostrazione dato che è una riformulazione del principio del minimo su $\mathbb{N}$.

Legame con le Congruenze

$a\equiv b(\text{mod n})\iff n|a-b\iff \exists q\in \mathbb{Z}t.c.a-b=qn$ ovvero il resto della divisione euclidea di $a-b$ per $n$ è 0.

Ricordiamo inoltre che la congruenza è una relazione d’equivalenza.

Esempio Congruenza Modulo 2

Nota, con la notazione $2\mathbb{Z}$ indichiamo l’insieme di tutti i numeri

$\mathbb{Z}=\underset{\text{pari}}{\underbrace{2\mathbb{Z}}}⨆\underset{\text{dispari}}{\underbrace{2\mathbb{Z}+1}}$

E notiamo che: $2\mathbb{Z}=\overline{0}$ e che $2\mathbb{Z}+1=\overline{1}$ notiamo infatti che $\mathbb{Z}\backslash {\equiv }_{\text{mod2}}=\{2\mathbb{Z},2\mathbb{Z}+1\}$

Ad esempio con la congruenza modulo 3 otteniamo $\mathbb{Z}\backslash {\equiv }_{\text{mod3}}=\{3\mathbb{Z},3\mathbb{Z}+1,3\mathbb{Z}+2\}$

In generale otteniamo che:

$$\mathbb{Z}\backslash {\equiv }_{\text{mod n}}=\{\underset{\overline{0}}{\underbrace{n\mathbb{Z}}},\underset{\overline{1}}{\underbrace{n\mathbb{Z}+1}},\dots ,\underset{\overline{n-1}}{\underbrace{n\mathbb{Z}+n-1}}\}$$

Notiamo che:

$${\overline{2}}_3=\{m\in \mathbb{Z}:m\equiv 2\text{ mod3}\}=\{m\in \mathbb{Z}:3|m-2\}$$

Con la notazione ${\overline{2}}_3$ indichiamo la classe di equivalenza di $2$ nell’applicazione congruenza modulo 3.

Esempio

$m=5,m-2=3,3|3$ quindi $5\in {\overline{2}}_3$ oppure $m=-1,m-2=-3,3|-3$ quindi $-1\in {\overline{2}}_3$

Compatibilità con la congruenza modulo n

Le operazione $+,\cdot ,-$ di $\mathbb{Z}$ sono compatibili con ${\equiv }_n$ con $n>0$ se rispettano delle proprietà:

1. $\forall a,a^{\prime }\in \mathbb{Z}$ abbiamo che $a\equiv a^{\prime }(\text{mod n})\iff -a\equiv -a^{\prime }(\text{mod n})$.
2. $a,a^{\prime },b,b^{\prime }\in \mathbb{Z}$ se $a\equiv a^{\prime }$ e $b\equiv b^{\prime }$ allora $a+b\equiv a^{\prime }+b^{\prime }$
3. $a,a^{\prime },b,b^{\prime }\in \mathbb{Z}$ se $a\equiv a^{\prime }$ e $b\equiv b^{\prime }$ allora $ab\equiv a^{\prime }{b}^{\prime }$

In tutti i casi intendiamo ${\equiv }_n$

Dimostrazione di 2

$a{\equiv }_n{a}^{\prime }\iff n|a^{\prime }-a$ e allo stesso modo $b{\equiv }_n{b}^{\prime }\iff n|b^{\prime }-b$ quindi:

$$\begin{array}{rl}& \text{Sappiamo che }a{\equiv }_n{a}^{\prime }\iff n|a^{\prime }-a\\ & \text{E che }b{\equiv }_n{b}^{\prime }\iff n|b^{\prime }-b\\ & \text{Inoltre:}\\ & n|a^{\prime }-a\iff \exists k\in \mathbb{Z}t.c.a^{\prime }-a=nk\\ & n|b^{\prime }-b\iff \exists k^{\prime }\in \mathbb{Z}t.c.b^{\prime }-b=n{k}^{\prime }\\ & \\ & \text{Addizionando termine a termine:}\\ & a^{\prime }+b^{\prime }-(a+b)=n(k+k^{\prime })\iff n|n(k+k^{\prime })\\ & \text{Quindi dato che n divide }{a}^{\prime }+b^{\prime }-(a+b)\text{ otteniamo che:}\\ & a^{\prime }+b^{\prime }{\equiv }_{n}a+b\end{array}$$

---

Adesso prendiamo l’insieme $\mathbb{Z}\backslash n\mathbb{Z}$ e data $\overline{a}\in \mathbb{Z}\backslash n\mathbb{Z}$ definiamo la classe $-(\overline{a}):=\overline{(-a)}$, questa applicazione $\mathbb{Z}\backslash n\mathbb{Z}\to \mathbb{Z}\backslash n\mathbb{Z}$ è ben definita ed è l’operazione di opposto.

Date le classi $\overline{a},\overline{b}\in \mathbb{Z}\backslash n\mathbb{Z}$ definiamo $\overline{a}+\overline{b}:=\overline{a+b}$ ed è ben definito quindi è indipendente dalla scelta di un rappresentante. Dimostriamolo:

$$\begin{array}{rl}& \text{Scelgo }{a}^{\prime }\in \overline{a},b^{\prime }\in \overline{b}\text{ quindi }(\overline{a}=\overline{a^{\prime }},\overline{b}=\overline{b^{\prime }})\\ & \overline{a^{\prime }+b^{\prime }}=\{m:n|m-a^{\prime }-b^{\prime }\}=\{m:n|m-a-b\}\iff \overline{a+b}=\overline{a^{\prime }+b^{\prime }}\end{array}$$

Definiamo inoltre una funzione che date $\overline{a},\overline{b}\in \mathbb{Z}\backslash n\mathbb{Z}$ allora $\overline{a}\cdot \overline{b}=\overline{a\cdot b}$, che è sempre ben definita.

Teorema

$(\mathbb{Z}\backslash n\mathbb{Z},+,-,\cdot ,\overline{0},\overline{1})$ è un anello.

Alcuni sottoinsiemi di $\mathbb{Z}$

$$\begin{array}{rl}& n\mathbb{Z}=\{m\in \mathbb{Z}t.c.\exists k\in \mathbb{Z}\text{ con }m=kn\}=\text{multipli di }n\\ & \mathbb{Z}\backslash \{0\}={\mathbb{Z}}^{\ast }\end{array}$$

Esercizio

Dati $a,b\in {\mathbb{Z}}^{\ast }$ con $a|b\iff b\mathbb{Z}\subset a\mathbb{Z}$:

$$\begin{array}{rl}& \text{Supponiamo che }a|b\text{ allora }\exists k\in \mathbb{Z}t.c.b=ka\\ & \text{Sia }{b}^{\prime }\in b\mathbb{Z}\text{ allora }\exists l\in \mathbb{Z}t.c.b^{\prime }=lb\text{ ma sappiamo che }b=ka\text{ quindi:}\\ & b^{\prime }=\underset{:=l^{\prime }}{(lk)}a\Rightarrow b^{\prime }\in a\mathbb{Z}\end{array}$$

---

Adesso vediamo insiemi nella forma $a\mathbb{Z}+b\mathbb{Z}:=\{m\in \mathbb{Z}:\exists k,k^{\prime }\in \mathbb{Z}\text{ con }m=ka+k^{\prime }b\}$.

Ad esempio possiamo scrivere che $2\mathbb{Z}+3\mathbb{Z}=\{0,2,4,6,\dots ,-2,-4,-6,\dots ,3,6,9,-3,-6,-9,\dots ,5,8,7,\dots \}=\mathbb{Z}$

Questo perché appunto prendiamo ogni volta due valori $k,k^{\prime }$ con i quali moltiplicare 2 e 3 in questo caso, e sempre in questo caso notiamo che stiamo sommando i numeri pari e quelli dispari quindi otteniamo tutti i numeri.

$a\mathbb{Z}+b\mathbb{Z}=MCD(a,b)\mathbb{Z}$ quindi ad esempio nel caso di prima $MCD(2,3)=1$ e infatti come abbiamo notato $2\mathbb{Z}+3\mathbb{Z}=1\mathbb{Z}$

Lemma:

Poniamo $\mathcal{E}:=a\mathbb{Z}+b\mathbb{Z}$ con $ab\ne 0$ allora esiste $\delta \in {\mathbb{N}}^{\ast }$ unico t.c. $\mathcal{E}=\delta \mathbb{Z}$.

Dimostrazione:

$$\begin{array}{rl}& \text{Poniamo }{\mathcal{E}}^{\ast }:=\mathcal{E}\cap {\mathbb{N}}^{\ast }\subset {\mathbb{N}}^{\ast }\\ & \text{Sappiamo che }{\mathcal{E}}^{\ast }\text{ sicuramente non eˋ vuoto}\\ & \text{Infatti se }a,b>0\text{ esiste una coppia }(k,k^{\prime })\in {\mathbb{N}}^{2}t.c.\underset{\in {\mathcal{E}}^{\ast }}{\underbrace{ka+k^{\prime }b}}>0\\ & \text{Se invece }a>0,b<0\text{ allora esiste }(k,k^{\prime })\in \mathbb{N}\times (-\mathbb{N})\\ & \text{Ci sono ancora 2 casi semplice che non vediamo}\\ & \\ & \text{Adesso poniamo }\delta =min({\mathcal{E}}^{\ast })\text{ ed eˋ ben definito in }{\mathbb{N}}^{\ast }\text{(principio del minimo)}\\ & \text{Osserviamo che }\delta <|a|,\delta <|b|\text{ infatti }|a|,|b|\in {\mathcal{E}}^{\ast }\\ & \\ & \text{Diciamo che }\delta |a\text{ e per il principio della divisione euclidea:}\\ & a=q\delta +rr\in \{0,\dots ,\delta -1\}\text{ dobbiamo quindi dimostrare che }r=0\\ & \text{Notiamo che }r=a-q\delta \\ & \\ & a\in \mathcal{E}\\ & \delta \in {\mathcal{E}}^{\ast }\subset \mathcal{E}=a\mathbb{Z}+b\mathbb{Z}\text{ quindi:}\\ & \delta =\underset{\in \mathbb{Z}}{\mathrm{ua}}+\underset{\in \mathbb{Z}}{\mathrm{vb}}\\ & \\ & r=a-q(ua+vb)=a(1-qu)+b(-qv)\Rightarrow r\in \mathcal{E}\\ & \text{Quindi dato che }r\text{ puoˋ essere o uguale a 0 o positivo}:\\ & \text{Se}=0\text{ abbiamo finito dato che }\delta |a\\ & \text{Altrimenti se > 0 otteniamo che }r\in {\mathcal{E}}^{\ast }\text{ e quindi }r>\delta \text{ ma eˋ impossibile per la definizione di r iniziale}\end{array}$$

Per la stessa ragione abbiamo che $\delta |b$.

$$\begin{array}{rl}& \forall \alpha ,\beta \in \mathbb{Z}\delta |\alpha a+\beta b\Rightarrow \mathcal{E}\subset \delta \mathbb{Z}(\text{ Per la dimostrazione di prima }a|b\iff b\mathbb{Z}\subset a\mathbb{Z})\\ & \text{D’altronde }\delta \in \mathcal{E}\iff \delta =ka+k^{\prime }b\\ & \forall l\in \mathbb{Z},l\delta =lka+l{k}^{\prime }b\Rightarrow l\delta \in \mathcal{E}\Rightarrow \delta \mathbb{Z}\subset \mathcal{E}\\ & \text{ Se i multipli di }\delta \text{ sono elementi di }\mathcal{E}\text{ allora }\delta \mathbb{Z}\text{ eˋ contenuto in }\mathcal{E}.\\ & \text{Abbiamo ottenuto quindi che }\mathcal{E}\subset \delta \mathbb{Z}\text{ e che }\delta \mathbb{Z}\subset \mathcal{E}\text{ quindi }\mathcal{E}=\delta \mathbb{Z}\end{array}$$

Massimo Comun Divisore

Data $(a,b)\in \mathbb{Z}\times \mathbb{Z}$ con $(a,b)\ne (0,0)$

Definizione

$d\in {\mathbb{N}}^{\ast }$ è MCD di $a$ e $b$ se:

1. $d|a$ e $d|b$
2. Se $d^{\prime }\in {\mathbb{N}}^{\ast }$ t.c. $d^{\prime }|a$ e $d^{\prime }|b$ allora $d^{\prime }|d$

Lemma: Se $d$ soddisfa (1) e (2) allora è unicamente determinato

Dimostrazione

Supponiamo che $d_1,d_2$ soddisfano (1) e (2) e mostriamo che $d_1=d_2$

$$\begin{array}{rl}& \text{Si ha che:}\\ & d_2|d_1\text{ e che }{d}_1|d_2\Rightarrow \{d_1,-d_1\}=\{d_2,-d_2\}\Rightarrow d_1=d_2\text{ Dimostrato sopra nelle proprietaˋ}\end{array}$$

Si scrive $d=MCD(a,b)$, inoltre se $MCD(a,b)=1$ si dice che $a,b$ sono primi fra loro (co-primi).

Lemma:

$$\begin{array}{rl}& \delta =MCD(a,b)\\ & a\mathbb{Z}+b\mathbb{Z}=\delta \mathbb{Z}(\delta >0;a,b\ne 0)\end{array}$$

Dimostrazione

$$\begin{array}{rl}& \delta \mathbb{Z}=a\mathbb{Z}+b\mathbb{Z}\supset a\mathbb{Z}\Rightarrow \delta |a\\ & \text{Allo stesso modo }\delta \mathbb{Z}=a\mathbb{Z}+b\mathbb{Z}\supset b\mathbb{Z}\Rightarrow \delta |b\\ & \text{Abbiamo quindi verificato la prima condizione del MCD }\\ & \\ & \text{Sia }{d}^{\prime }\in {\mathbb{N}}^{\ast }t.c.d^{\prime }|a,d^{\prime }|b\\ & d^{\prime }|a\iff a\mathbb{Z}\subset d^{\prime }\mathbb{Z}\\ & d^{\prime }|b\iff b\mathbb{Z}\subset d^{\prime }\mathbb{Z}\\ & \text{Quindi}\\ & \underset{\delta \mathbb{Z}}{\underbrace{a\mathbb{Z}+b\mathbb{Z}}}\subset \underset{d^{\prime }\mathbb{Z}}{\underbrace{d^{\prime }\mathbb{Z}+d^{\prime }\mathbb{Z}}}\Rightarrow d^{\prime }|\delta \\ & \text{Abbiamo quindi verificato anche la seconda condizione}\end{array}$$

Algoritmo di Euclide per trovare MCD

Possiamo vederlo come una funzione che prende in input $a,b>0$ e restituisce un $\delta =MCD(a,b)$

Esempio

Prendendo l’esempio sopra allora sappiamo che $\exists u,v\in \mathbb{Z}t.c.3=3522u+321v$ ma come si calcolano? Identità di Bèzout

Lemma di Gauss: Se $a,b\in {\mathbb{Z}}^X$ e $c\in \mathbb{Z}$ e se $MCD(a,b)=1$ allora $a|bc\Rightarrow a|c$

Dimostrazione

Sappiamo che $MCD(a,b)=1$ e quindi sappiamo che $a\mathbb{Z}+b\mathbb{Z}=\delta \mathbb{Z}=\mathbb{Z}$ (teoremi visti precedentemente). Questo inoltre significa che $\exists u,v\in \mathbb{Z}t.c.au+bv=1$, allora:

$$\begin{array}{rl}& \text{Moltiplichiamo per c}\\ & auc+\underset{\text{Divisibile per a}}{\underbrace{bc}}v=c\\ & \text{Questo significa che }\exists kt.c.b=k\cdot a\\ & auc+kav=c\to a\underset{\exists lt.c.c=al}{\underbrace{(uc+kv)}}=c\\ & \text{Questo significa quindi che }a|c\end{array}$$

Lemma: Dato $p\in \mathbb{N},p>1$ allora $p$ è irriducibile $\Rightarrow p$ è primo.

Dimostrazione

Prima di tutto dimostriamo una proprietà utile per dopo: Se $p$ è irriducibile e $p\nmid a$ allora $a\mathbb{Z}+p\mathbb{Z}=\mathbb{Z}\iff MCD(a,p)=1$, altrimenti $\exists \delta >1t.c.\delta |ae\delta |p$ ma visto che $p$ è irriducibile allora $\delta$ è $=p\Rightarrow p|a$ ma questo va in contraddizione con l’ipotesi ovvero che $p$ non divide $a$.

Adesso passiamo alla dimostrazione del Lemma.

Supponiamo che $p|ab$ con $p$ irriducibile. Allora $p$ deve dividere $a$ o $b$, senza perdere generalità possiamo quindi supporre che non divide $a$ e dobbiamo dimostrare che necessariamente divide $b$.

$$\begin{array}{rl}& a\mathbb{Z}+p\mathbb{Z}=\mathbb{Z}\\ & \text{Moltiplichiamo per b}\\ & \underset{\subset p\mathbb{Z}}{\underbrace{\underset{p|ab}{\underbrace{ab}}\mathbb{Z}+\underset{p|pb}{\underbrace{pb}}\mathbb{Z}}}=b\mathbb{Z}\\ & \text{Quindi dato che }b\mathbb{Z}\subset p\mathbb{Z}\Rightarrow p|b\end{array}$$

Esercizio

Calcolare $(\mathbb{Z}\backslash N\mathbb{Z}{)}^X$ con $N\in \mathbb{N}$

Premesse:

• $A=\mathbb{Z}\backslash N\mathbb{Z}=\mathbb{Z}\backslash {\equiv }_N$
• $[a]+[b]=[a+b]$ e $[a]\cdot [b]=[a\cdot b]$
• Con l’elemento $[0]=(N\mathbb{Z})$ per l’elemento neutro di $+$ e con l’elemento $[1](=N\mathbb{Z}+1)$ per l’elemento neutro di $\cdot$, si ottiene che $A$ è un anello commutativo unitario

Si cerca:

• $A^X=\{[n]t.c.\exists [m]\text{ con }[m]\cdot [n]=[1]\}$ “Insieme delle unità”

1. Sia $[a]\in (\mathbb{Z}\backslash N\mathbb{Z}{)}^X$ allora esiste $b\in \mathbb{Z}\backslash N\mathbb{Z}$ t.c. $[a]\cdot [b]=[1]$, $[ab]=[1]\iff N|ab-1\iff \exists k\in \mathbb{Z}$ t.c. $kN=ab-1$. (È invertibile se e solo se scelto un qualsiasi rappresentante, quando faccio $ab-1$ è divisibile per N).

   Spostando i termini di prima otteniamo $ab-kN=1$ che è un’identità di Bèzout per $a,N$ e questo significa che $a,N$ sono primi fra loro perché il loro MCD è 1.

Quindi otteniamo che $(\mathbb{Z}\backslash N\mathbb{Z}{)}^X=\{[a]:a\in \mathbb{Z}eMCD(a,N)=1\}$.

Esiste quindi un’applicazione biiettiva tra $\{r\in \{0,\dots ,N-1\}t.c.MCD(r,N)=1\}$ e $(\mathbb{Z}\backslash N\mathbb{Z}{)}^X$, $r\to [r]$.

Esempio

$N=24=2^3\cdot 3$, verificare che $(\mathbb{Z}\backslash 24\mathbb{Z}{)}^X=\{r:2\nmid r,3\nmid r\}$, quindi $(\mathbb{Z}\backslash 24\mathbb{Z}{)}^X=\{[5],[7],[11],[13],[17],[19],[23]\}$.

Cosa si osserva se N è primo?

• $N=p$ primo: Sia $r\in \{[1],\dots ,[p-1]\}$ allora $MCD(p,r)=1$ altrimenti qualora si avesse $\delta =MCD(p,r)>1$ avrei che $\delta |p,\delta |r\Rightarrow \delta =p$ e quindi si avrebbe che $p|r$ ma $r<p$ siccome è resto e quindi è una contraddizione, abbiamo quindi che $r,p$ sono coprimi.

Si ottiene $(\mathbb{Z}\backslash p\mathbb{Z}{)}^X=\{[r]:1\le r\le p-1\}(\forall r\in \mathbb{Z}\backslash p\mathbb{Z}-\{0\},r\text{ eˋ invertibile})$

Terminologia

Dato un anello $A$ commutativo t.c. $\forall a\in A\backslash \{0\}$ invertibile, si dice campo. Ad esempio $\mathbb{Z}\backslash p\mathbb{Z}={\mathbb{F}}_p$ è un campo.

---

Esercizio 5

Dimostrare il Piccolo Teorema di Fermat.

Dato un numero $p$ primo e un intero $n$ tali che $n^p\equiv n\text{(mod p)}$ mostrare che se $n$ e $p$ sono primi fra loro allora $n^{p-1}\equiv 1\text{(mod p)}$.

A cosa serve il teorema di Fermat? Serve a ridurre l’esponente nel calcolo delle potenze quando il numero è molto grande.

---

Proprietà: Sappiamo che ${\mathbb{F}}_p=\mathbb{Z}/p\mathbb{Z}$ è un campo ovvero ${\mathbb{F}}_p^X=\{[1],[2],\dots ,[p-1]\}$ inoltre sappiamo anche che $([a]+[b]{)}^p=[a{]}^p+[b{]}^p$ con $[a],[b]\in {\mathbb{F}}_p$, (non vera in $\mathbb{Z}$).

Scegliamo come $a,b$ come rappresentanti e scriviamo:

$$(a+b{)}^p=a^p+(\genfrac{}{}{0ex}{}{p}{1})\cdot a^{p-1}\cdot b+(\genfrac{}{}{0ex}{}{p}{2})\cdot a^{p-2}\cdot b^2+\cdots +(\genfrac{}{}{0ex}{}{p}{p-2})\cdot a^2\cdot b^{p-2}+(\genfrac{}{}{0ex}{}{p}{p-1})\cdot a\cdot b^{p-1}+b^p$$

• Prendiamo $0<i<p$ e scriviamo $\left(\genfrac{}{}{0ex}{}{p}{i}\right)=\frac{p!}{i!\cdot (p-i)!}\in \mathbb{N}$ e quindi si ha che $p|i!\cdot (p-i)!$
• Supponiamo che $1\le i\le p-1$ e inoltre $i\ne i(i-1)\dots 3\cdot 2\cdot 1$ e quindi siccome $p>i$ ed $i$ si scompone in tutti fattori più piccoli di $p$ e quindi non divisibili per $p$ (nemmeno il loro prodotto dato che $p$ è primo) abbiamo che $p\nmid i$
• Allo stesso modo otteniamo che $p>p-i$ e quindi $p\nmid (p-i)!$

Quindi abbiamo che:

$$p\ne \underset{a}{\underbrace{k}}\cdot \underset{b}{\underbrace{i!\cdot (p-i)!}}\exists k\in N^{\ast }$$

E per le condizioni viste sopra sappiamo che $p\nmid b$, ma per definizione di fattoriale sappiamo che $p|p!=ab$, quindi visto che $p$ è primo e non divide $b$ allora deve sicuramente dividere $a$ per il lemma di Gauss.

Noi sappiamo però che $a=k=\left(\genfrac{}{}{0ex}{}{p}{i}\right)$ dato che $\left(\genfrac{}{}{0ex}{}{p}{i}\right)=\frac{p!}{i!(p-i)!}\to p!=\left(\genfrac{}{}{0ex}{}{p}{i}\right)\cdot i!\cdot (p-i)!$.

Quindi siccome $p$ dividi tutti i $\left(\genfrac{}{}{0ex}{}{p}{i}\right)$ questi si riducono tutti a $\overline{0}$ nella formula vista sopra, ad eccezione del primo e l’ultimo.

Abbiamo dimostrato che $([a]+[b]{)}^p=[a{]}^p+[b{]}^p$ dato che se $1\le i\le p-1$ e $p$ primo abbiamo che $\left(\genfrac{}{}{0ex}{}{p}{i}\right)=\left(\genfrac{}{}{0ex}{}{p}{p-i}\right){\equiv }_{p}0$.

---

Tornando alla dimostrazione del teorema di Fermat

$$\begin{array}{rl}& [0{]}^p=[0]\\ & [1{]}^p=[1]\\ & [2{]}^p=([1]+[1]{)}^p=[1{]}^p+[1{]}^p=[1]+[1]=[2]\end{array}$$

Facciamo una dimostrazione per induzione, la nostra ipotesi è $[n-1{]}^p=[n-1]$, quindi:

$$[n{]}^p=([n-1]+[1]{)}^p=[n-1{]}^p+[1{]}^p=[n-1]+[1]=[n]$$

In questo modo abbiamo dimostrato che $\forall n\in \mathbb{Z},n^p{\equiv }_{p}n$ con $p$ primo.

Precisazione

Se $[n]\ne [0]$ in ${\mathbb{F}}_p$ ovvero se $[n]\in {\mathbb{F}}_p^X$ allora $[n]$ è invertibile di inverso $[n{]}^{\prime }$, per il PTF sappiamo che $[n{]}^p=[n]$, moltiplichiamo per $[n{]}^{\prime }$:

$$\underset{[n{]}^{\prime }[n][n{]}^{p-1}=[n{]}^{p-1}}{\underbrace{[n{]}^p[n{]}^{\prime }}}=\underset{1}{\underbrace{[n][n{]}^{\prime }}}$$

Otteniamo quindi che $[n{]}^{p-1}=[1]$

Difetti del PTF

Se $[a]\in F_p^X$ e quindi è invertibile, calcolare il suo inverso $[a{]}^{-1}$ usando il PTF, ricordiamo che $[a{]}^{p-1}=[1]$

So che $[a{]}^{p-1}=[a{]}^{p-2}\cdot [a]$, quindi:

$$\begin{array}{rl}& [1]=\underset{\text{Inversi}}{\underbrace{[a{]}^{p-2}\cdot [a]}}\\ & [a{]}^{-1}=[a{]}^{p-2}\end{array}$$

Questo però per numeri molto grandi risulta scomodo, infatti se ad esempio vogliamo calcolare $[2{]}^{-1}$ con $p=691$, dobbiamo calcolare $[2{]}^{p-2}=[2{]}^{689}$.

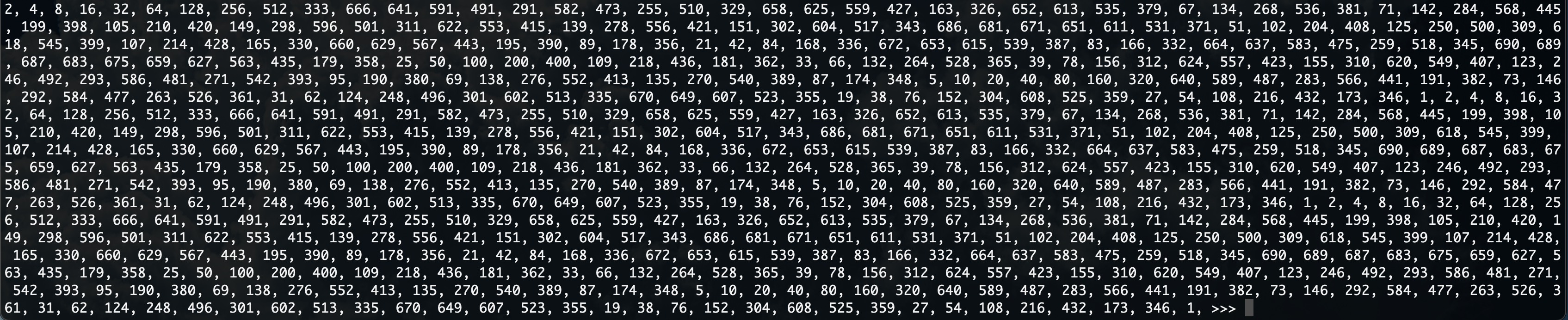
Svolgendo i calcoli però, ovvero calcolando $2^i\%691$ per $i$ che va da $1$ a $690$ notiamo che si l’ultima è 1 e quindi il suo inverso (689) ma ci sono anche altri 1 prima, perché le classi sono cicliche.

Esercizio

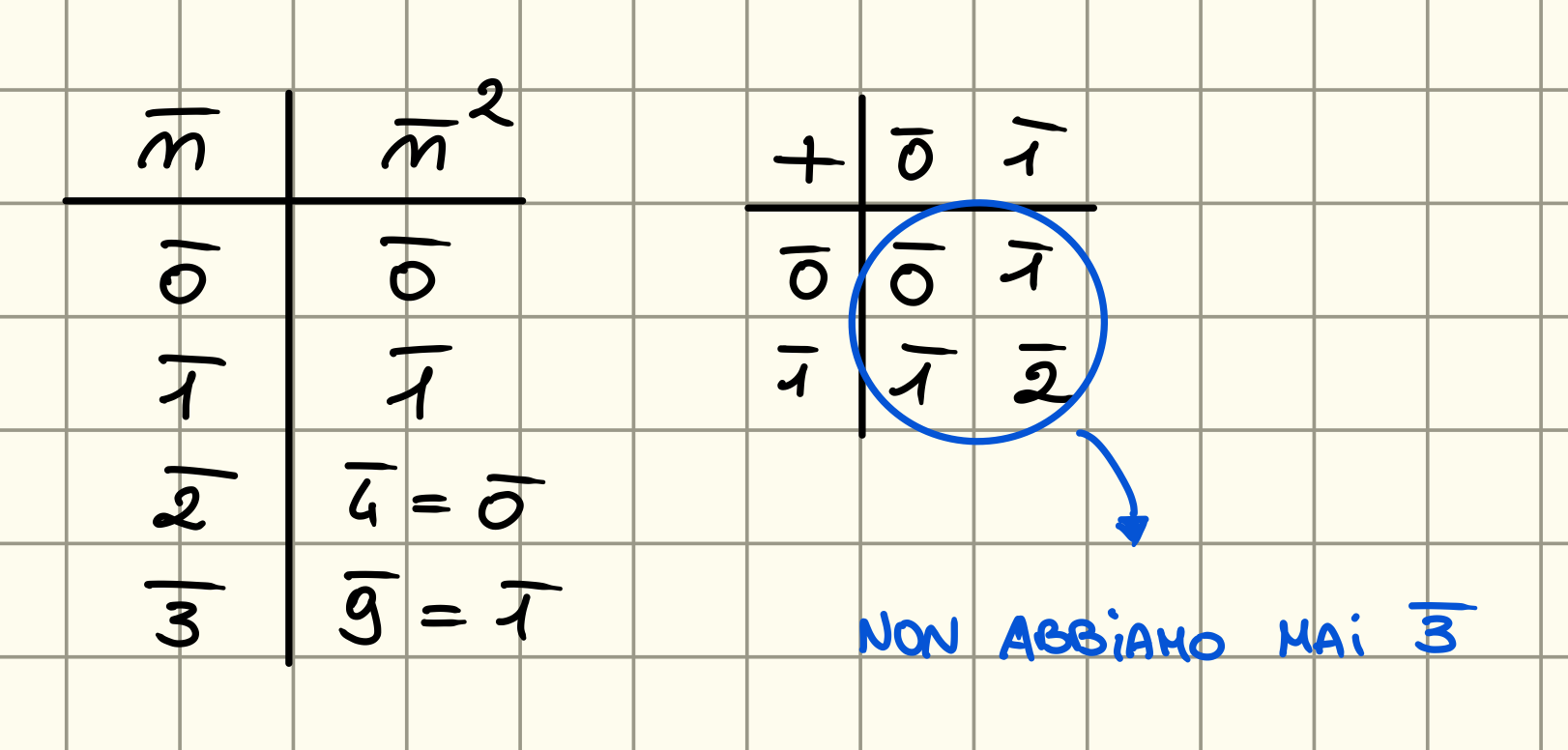
Dimostrare che in $4\mathbb{Z}+3$ nessun intero è somma di due quadrati.

Calcoliamo le classi dei resti modulo 4 e i loro quadrati.

Successione di Fibonacci

La successione di Fibonacci è definita induttivamente da $F_0=0,F_1=1,F_n=F_{n-1}+F_{n-2}$, i numeri della successione di Fibonacci hanno alcune proprietà:

• $MCD(F_m,F_n)=F_{MCD(m,n)}$
• $MCD(F_m,F_{m+1})=F_1=1$

Dimostriamolo per Induzione

Quindi sappiamo che:

$$F_0=0;F_1=1;F_{n+1}=F_n+F_{n-1}$$

Definiamo $MCD(F_n,F_{n+1})={\delta }_n$, possiamo inoltre scrivere $\mathbb{Z}{F}_n+\mathbb{Z}{F}_{n+1}=\mathbb{Z}{\delta }_n$ e dobbiamo dimostrare che $\mathbb{Z}{\delta }_n=1\mathbb{Z}$ ovvero che il loro $MCD$ è 1.

$$\begin{array}{r}\mathbb{Z}{F}_n+\mathbb{Z}{F}_{n+1}=\{a{F}_n+b{F}_{n+1}:a,b\in \mathbb{Z}\}=\underset{\text{Dobbiamo dimostrare che }=\mathbb{Z}{F}_{n-1}+\mathbb{Z}{F}_n}{\underbrace{\{a{F}_n+b\stackrel{\text{Definizione Fib.}}{\overbrace{(F_n+F_{n-1})}}:a,b\in \mathbb{Z}\}}}\end{array}$$

Quell’insieme possiamo scriverlo come:

$$\{(a+b)F_n+b{F}_{n-1}:a,b\in \mathbb{Z}\}$$

E quindi possiamo scrivere:

$$\underset{A}{\underbrace{\{(a+b)F_n+b{F}_{n-1}:a,b\in \mathbb{Z}\}}}\subseteq \mathbb{Z}{F}_{n-1}+\mathbb{Z}{F}_n$$

Quindi l’insieme a sinistra è sicuramente sottoinsieme di quello a destra, ma per dimostrare che sono uguali devo dimostrare che esiste un’applicazione biiettiva $f:{\mathbb{Z}}^2\to {\mathbb{Z}}^2$ che manda $(a,b)\to (\underset{u}{\underbrace{a+b}},\underset{v}{\underbrace{b}})$. Sia $f({\mathbb{Z}}^2)$ l’immagine noi sappiamo che $A=\{u{F}_{n-1}+v{F}_n:(u,v)\in {\mathbb{Z}}^2\}$ quindi se dimostriamo che l’applicazione è suriettiva abbiamo dimostrato che qualsiasi $a,b$ prendo raggiungo tutti gli $u,v$ e quindi i due insiemi sono uguali.

Dimostreremo che l’applicazione è biiettiva che comprende anche suriettiva.

Richiamo

$A\stackrel{f}{\to }B$ è biiettiva $\iff \forall b\in B,f^{-1}(\{b\})$ è un singleton, ma deve esserci anche un’inversa $\exists g:B\to A$ t.c. $f\circ g=I{d}_B$ e simultaneamente $g\circ f(A)=I{d}_A$.

Quindi noi sappiamo che $f(a,b)=(a+b,b)=:(u,v)$ e questo è equivalente a un sistema:

$$\{\begin{array}{l}a+b=u\\ b=v\end{array}\iff \{\begin{array}{l}a=u-v\\ b=v\end{array}$$

Adesso poniamo l’inversa $g:{\mathbb{Z}}^2\to {\mathbb{Z}}^2$ e quindi abbiamo le coppie $(u,v)\to (u-v,v)$ adesso verifichiamo se le funzioni composte ci danno le Identità.

$$\begin{array}{rl}& (f\circ g)(u,v)=f(g(u,v))=f(u-v,v)=(u-v+v,v)=(u,v)\text{ La prima eˋ verificata}\\ & (g\circ f)(a,b)=g(f(a,b))=g(a+b,b)=(a+b-b,b)=(a,b)\text{ Anche la seconda eˋ verificata}\end{array}$$

Quindi l’applicazione è biiettiva e quindi suriettiva e quindi i due insiemi sono uguali.

Sapendo che è sempre verificato possiamo sempre diminuire il numero di Fibonacci e ottenere:

$$\forall n>0F_{n+1}\mathbb{Z}+F_n\mathbb{Z}=F_n\mathbb{Z}+F_{n-1}\mathbb{Z}=F_{n-1}\mathbb{Z}+F_{n-2}\mathbb{Z}=\cdots =F_1\mathbb{Z}+F_0\mathbb{Z}$$

Quindi $F_1\mathbb{Z}+\{0\}=\mathbb{Z}$ che può essere anche scritto $\forall n>0,F_n\mathbb{Z}+F_{n-1}\mathbb{Z}=\mathbb{Z}$ e questo equivale anche a dire che $MCD(F_{n-1},F_n)=1$.

Teorema Fondamentale Dell’Aritmetica

$\forall a\in {\mathbb{Z}}^{\ast }$ abbiamo che:

1. $I_a=\{p\text{ primo}:p|a\}$ è finito, quindi c’è solo un numero finito di primi che dividono $a$.
2. Inoltre $a=(\pm 1)\cdot \prod _p{p}^{v_p(a)}$ dove $v_p(a)$ è un certo esponente in $\mathbb{N}$ e sono unicamente determinati. Ovvero ogni numero intero diverso da 0 è il prodotto di alcuni numeri primi elevati a determinati esponenti.

Notiamo che nella seconda condizione i numeri primi sono infiniti e quindi otterremmo un valore infinito, però ad un certo punto $v_p(a)$ sarà uguale a 0 e quindi avremo un numero finito di primi e poi un numero infinito di 1 che non cambia il nostro valore. Formalizziamolo

Osservazione

Si sa che $\mathbb{P}=\{p\in \mathbb{N},\text{p primo}\}$ è infinito però siccome $\forall a\in {\mathbb{Z}}^{\ast }$ abbiamo che $I_a$ è finito:

$$\prod _p{p}^{v_p(a)}=\underset{\text{Questo eˋ finito}}{\underbrace{\prod _{p\in I_a}{p}^{v_p(a)}}}\cdot \underset{\text{Questo eˋ infinito}}{\underbrace{\prod _{p\notin I_a}{p}^{v_p(a)}}}$$

Però nell’insieme infinito avremo che $v_p(a)=0$ e quindi tutto quel prodotto sarà uguale a $1\cdot ...\cdot 1=1$.

Esempi

$$\begin{array}{rl}& a=1\\ & 1=+1\cdot \prod _p{p}^{v_p(1)}\text{ Con }{v}_p(1)=0\forall p\\ & \text{Questo ci dice che }{I}_1=\varnothing \text{ Ovvero non abbiamo nessun primo}\end{array}$$ $$\begin{array}{rl}& a=2\\ & 2=+1\cdot \prod _p{p}^{v_p(2)}\\ & v_p(2)=1\text{ se }p=2,\text{altrimenti }{v}_p(2)=0\\ & \\ & \text{Quindi possiamo scrivere }2=2\cdot \prod _{p\ne 2}{p}^0\end{array}$$ $$\begin{array}{rl}& a=7!=7\cdot 5\cdot 3^2\cdot 2^4\\ & \text{Possiamo definire:}\\ & v_p(a)=\{\begin{array}{l}1p=7\\ 1p=5\\ 2p=3\\ 4p=2\\ 0p>7\end{array}\\ & \text{Possiamo poi utilizzare la formula:}\\ & 7!=+1\cdot \prod _p{p}^{v_p(a)}\end{array}$$

Cosa possiamo dedurre con queste notazioni? Scriviamo due numeri $a,b$:

$$\begin{array}{rl}& a=\prod _p{p}^{v_p(a)}b=\prod _p{p}^{v_p(b)}\\ & \\ & \text{Scriviamo }a\cdot b=\prod _p{p}^{v_p(a)}\cdot \prod _{p^{\prime }}{p^{\prime }}^{v_{p^{\prime }}(b)}\\ & \\ & \text{Che eˋ uguale a: }\prod _p{p}^{v_p(a)+v_p(b)}\\ & \\ & \text{Cosa ci dice questo? Che }{v}_p(ab)=v_p(a)+v_p(b)\end{array}$$

Vediamo un esempio:

$$\begin{array}{rl}& a=12=2^2\cdot 3\\ & b=15=5\cdot 3\\ & \\ & \{\begin{array}{l}{v}_2(a)=2\\ v_3(a)=1\\ v_5(a)=0\end{array}\{\begin{array}{l}{v}_2(b)=0\\ v_3(b)=1\\ v_5(b)=1\end{array}\\ & \\ & v_p(a\cdot b)=v_p(12\cdot 15)=v_p(a)+v_p(b)\\ & \\ & \text{Otteniamo quindi, facendo le somme:}\\ & v_2(ab)=2;v_3(ab)=1;v_5(ab)=1;v_p(ab)=0\text{ Quando }p>5\end{array}$$

---

Dimostriamo il teorema ovvero che:

$$a=(\pm 1)\cdot \prod _p{p}^{v_p(a)}$$

Per prima cosa dimostriamo che $I_a$ è un insieme finito. (1)

Supponiamo per assurdo che $I_a$ sia infinito e questo significa che esiste una collezione infinita di primi $p$ t.c. $p|a$ e questo significa che ogni $p\le a$. Supponiamo anche $a>0$.

Abbiamo ottenuto una contraddizione, infatti essendo $a$ un intero, non esiste un numero infinito di numero inferiori a lui. Abbiamo provato che $I_a$ è finito.

Adesso dimostriamo la fattorizzazione per induzione (2).

Per $a=1$ lo abbiamo già mostrato prima, abbiamo che per ogni $\forall p,v_p(a)=0$ e otteniamo un prodotto infinito di 1 che fa 1.

Adesso supponiamo che $a>1$, abbiamo due casi:

• Se $a$ è primo non abbiamo nulla da dimostrare infatti il $v_p(a)$ è sempre 0 tranne quando $p=a$.

• Se $a$ non è primo allora non è irriducibile e allora posso scrivere $a=u\cdot v$ con $1<u<a,1<v<a$ ovvero due divisori di $a$ diversi da 1.

  Per ipotesi induttiva visto che $u,v<a$ posso scrivere:

  $$\begin{array}{rl}& u=\prod _p{p}^{v_p(u)}\\ & v=\prod _p{p}^{v_p(v)}\\ & a=u\cdot v=\prod _p{p}^{v_p(u)+v_p(v)}\\ & \text{Per la formula di prima sappiamo che }{v}_p(uv)=v_p(u)+v_p(v)\\ & \text{Quindi dato che }uv=a\text{ allora quell’esponente eˋ }=v_p(a)\end{array}$$

---

Enunciato Teorema

$\forall a>0,\exists$ un numero finito di primi distinti $p_1,\dots ,p_r$ tali che $a=p_1^{{\alpha }_1},\dots ,p_r^{{\alpha }_r}$ e questa fattorizzazione è unicamente determinata.

Questo è un enunciato differente ma con lo stesso significato di quello visto sopra, ma qui dobbiamo numerare i $p$.

Esercizio

Prendiamo $a,b\in {\mathbb{N}}^{\ast }$ e quindi possiamo scriverli come:

$$\begin{array}{r}a=\prod _p{p}^{v_p(a)}\\ b=\prod _p{p}^{v_p(b)}\end{array}$$

Mostrare che $a|b\iff \forall p,v_p(a)\le v_p(b)$.

1:

Supponiamo che $v_p(a)\le v_p(b)$ e questo è equivalente a dire che $\underset{\in \mathbb{N}}{\underbrace{v_p(b)-v_p(a)}}\ge 0$ .

Adesso poniamo $k=\prod _p{p}^{v_p(b)-v_p(a)}$ e quindi l’esponente è un intero.

Adesso calcoliamo $k\cdot a$:

$$\prod _p{p}^{v_p(b)-v_p(a)}\cdot \prod _p{p}^{v_p(a)}=\prod _p{p}^{v_p(b)-\cancel{v_p(a)}+\cancel{v_p(a)}}=b$$

Questo implica che $b=k\cdot a,\exists k\in {\mathbb{N}}^{\ast }$ e quindi $a|b$.

2:

Supponiamo che $a|b$ questo implica che $b=k\cdot a,\exists k\in {\mathbb{N}}^{\ast }$, applichiamo il teorema fondamentale dell’aritmetica:

$$\prod _p{p}^{v_p(b)}=\prod _p{p}^{v_p(k)}\cdot \prod _p{p}^{v_p(a)}=\prod _p{p}^{v_p(k)+v_p(a)}$$

Per unicità della fattorizzazione (quando prendo un primo, gli esponenti devono essere uguali da entrambe le parti) $v_p(b)=\underset{\ge 0}{\underbrace{v_p(k)}}+v_p(a),\forall p$ quindi questo significa che $v_p(b)\ge v_p(a)$.

---

Esercizio

Prendiamo $a,b\in {\mathbb{N}}^{\ast }$ dimostriamo che:

$$MCD(a,b)=\prod _p{p}^{min(v_p(a),v_p(b))}$$

Come abbiamo definito $MCD(a,b)$? L’abbiamo definito come l’unico intero $\delta$ in $N^{\ast }$ tale $\delta |a,\delta |b$ (1) e $\forall d^{\prime }\in {\mathbb{N}}^{\ast }$ tale che $d^{\prime }|a,d^{\prime }|b$ allora $d^{\prime }|\delta$ (2)

Come traduciamo queste condizioni in termini di produttorie usando il teorema fondamentale?

Ricordiamo che nell’esercizio precedente abbiamo dimostrato che $a|b\iff \forall p,v_p(a)\le v_p(b)$, quindi:

1. Equivale a dire $\forall p,v_p(\delta )\le v_p(a)$ e $v_p(\delta )\le v_p(b)$
2. Se $d^{\prime }$ soddisfa la condizione 1 (al posto di $\delta$) allora soddisfa anche $v_p(d^{\prime })\le v_p(\delta )$

La condizione (1) ci suggerisce che $v_p(\delta )\le min(v_p(a),v_p(b))$ allora (2) vuol dire che se $d^{\prime }$ è tale che $v_p(d^{\prime })\le min(v_p(a),v_p(b))$ allora $v_p(d^{\prime })\le v_p(\delta )$

Quindi $\forall p,v_p(\delta )$ è il più grande degli interi $n$ t.c. $n\le min(v_p(a),v_p(b))$ questo implica che $v_p(\delta )=min(v_p(a),v_p(b))$.

Divisori di Zero

Iniziamo da degli esempi:

Prendiamo $\mathbb{Z}/6\mathbb{Z}=\{[0],[1],[2],[3],[4],[5]\}$, notiamo che ad esempio le classi $[2],[3]$ non sono nulle ma il loro prodotto da $[6]$ che è uguale a $[0]$. In $\mathbb{Z}$ questo non può accadere, non ci sono due elementi non nulli che moltiplicati fra loro danno come risultato zero, qui invece può succedere.

Definizione

Dato $A$ anello, $a\in A$ è divisore di zero se $\exists b\in A\backslash \{0\}t.c.ab=0_A$, non impostiamo che $a\ne 0$ perché vogliamo ammettere 0 come divisore di 0.

Esempi

In $\mathbb{Z}/6\mathbb{Z}$ come divisori di zero abbiamo $[0],[2],[3]$.

In $A$ qualsiasi $0_A$ è divisore di zero. Con $A\ne \{0\}$ ovvero quando i due elementi neutri sono distinti.

Invece, dove non abbiamo divisori di zero? Nei campi, se $A=K$ campo (ad esempio $A=\mathbb{Q},\mathbb{R},\mathbb{C},{\mathbb{F}}_p$ primo) cioè $\forall a\in K\backslash \{0\},a$ è invertibile ovvero $K^X=K^{\ast }$. L’unico di divisore di zero in un $K$ campo è $0_K$, perché?

Supponiamo di avere $a$ divisore di zero, allora $\exists b\ne 0t.c.ab=0$, però $b$ è invertibile perché non nullo, quindi $\exists b^{-1}\in K^{X}t.c.b\cdot b^{-1}=1$.

Adesso moltiplichiamo termine a termine $ab=0$ per $b^{-1}$ e otteniamo:

$$\begin{array}{rl}& a\cdot \stackrel{1}{\overbrace{b\cdot b^{\prime }}}=0\cdot b^{\prime }\\ & a\cdot 1=0\end{array}$$

Quindi se $a$ è divisore di 0 allora $a=0$.

---

In $\mathbb{Z}$ se $a$ è divisore di zero allora $a=0$ anche se $\mathbb{Z}$ non è campo, dimostriamolo:

Sia $a$ divisore di zero allora $\exists b\in {\mathbb{Z}}^{\ast }t.c.ab=0$, e anche $-a$ è divisore di zero:

$$\begin{array}{rl}& (-a)\cdot (-b)=a\cdot b=0\\ & \text{Questo vuol dire a divisore di zero}\iff -a\text{ eˋ divisore di zero}\end{array}$$

Possiamo supporre quindi, senza perdere generalità, che $a$ sia $\ge 0$.

Quindi abbiamo detto che $\exists b\ne 0t.c.ab=0$ e quindi possiamo scrivere:

$$0=a\cdot b=\underset{\text{a volte}}{\underbrace{b+b+\cdots +b}}\ge b>0$$

Se $a>0$ questo non è possibile e allora l’unica scelta che ci rimane è $a=0$, quindi abbiamo dimostrato che $\mathbb{Z}$ ha come unico divisore di zero, 0.

Definzione Dominio

Dato un anello $A\ne \{0\}$ si dice che è un dominio se l’unico divisore di zero in $A$ è zero. Quindi ogni campo è un dominio, ma anche $\mathbb{Z}$ è un dominio. Invece ad esempio $\mathbb{Z}/6\mathbb{Z}$ non è un dominio.

---

Se $a\in A$ non è divisore di zero e se $ax=0$ allora $x=0$, da questo possiamo scrivere il seguente lemma

Lemma - Legge di Cancellazione

Prendiamo $a\in A$ non divisore di zero, allora se $ab=ac\Rightarrow b=c$.

Dimostrazione:

Supponiamo $ab=ac$, che è equivalente a $a(b-c)=0$, se $a$ non è divisore di zero allora $b-c=0\Rightarrow b=c$.

Osservazione, questo implica la legge di cancellazione in $\mathbb{Z}$.

Risoluzione di Equazioni in A

Come anello $A$ prendiamo $A=\mathbb{Z},A=\mathbb{Z}/n\mathbb{Z}$.

Studieremo l’equazione lineare:

$$aX=ba,b\in A$$

$X$ viene detta Indeterminata. Se vogliamo risolverla significa che vogliamo trovare tutti gli $X$ tali che la soddisfano. Vediamo i casi semplici:

$$A=\mathbb{Z}:2X=3\text{ L’insieme delle soluzioni eˋ }\{x\in \mathbb{Z}:2x=3\}=\varnothing$$

Infatti sia $x$ soluzione dell’equazione $2x=3$ allora $x$ è un intero tale che moltiplicato per 2 mi dà 3 ovvero che $2|3$ che è impossibile.

Cambiamo l’equazione:

$$2X=6\text{ Soluzioni:}\{x\in \mathbb{Z}:2x=6\}=\{3\}$$

In questo caso abbiamo una soluzione, in $\mathbb{Z}$. Osserviamo che utilizzando il T.F.A (Teorema Fondamentale dell’Aritmetica) $6=2\cdot 3$ e sia $x$ una soluzione allora $2x=2\cdot 3$ e utilizzando la legge di cancellazione su $2$ otteniamo $x=3$.

In generale una soluzione di $aX=b$ (sempre con $A=\mathbb{Z}$) esiste $\iff a|b$. Infatti se l’insieme delle soluzioni è non vuoto e se $x$ è soluzione, si ha $ax=b\iff a|b$.

Allo stesso tempo se $a|b$ allora $\exists k\in \mathbb{Z}t.c.ak=b$ e posso prendere $x=k$.

---

Adesso vediamo cosa succede nel caso $A=\mathbb{Z}/n\mathbb{Z}$ con $n\in N^{\ast }$. Vogliamo risolvere:

$$aX=b$$

Nel caso in cui $A$ è un anello qualsiasi e $a\in A^X$ di inverso $a^{-1}$, possiamo moltiplicare termine a termine e ottenere:

$$\underset{1}{\underbrace{a^{-1}\cdot a}}\cdot X=b\cdot a^{-1}$$

E quindi otteniamo che $x=b\cdot a^{-1}$ che è un’unica soluzione.

Indeterminata X

Con $X$ indichiamo l’insieme delle soluzioni mentre con $x$ un elemento di questo insieme.

Se per esempio $A=K$ campo (anelli dove ogni elemento non nullo è invertibile, visto che un elemento invertibile non è divisore di zero allora un campo è sempre dominio di integrità, infatti l’unico divisore di zero è zero), allora in questo caso l’equazione $aX=b$ con $a\ne 0$ ammette sempre l’unica soluzione $x=a^{-1}\cdot b$.

Torniamo nel caso $\mathbb{Z}/n\mathbb{Z}$ e scriviamo la seguente

Proposizione:

$$aX=ba,b\in A=\mathbb{Z}/n\mathbb{Z}$$

L’equazione ammette soluzioni se e solo se dati $a=\overline{\alpha },b=\overline{\beta }(\alpha ,\beta \in \mathbb{Z})$, $MCD(\alpha ,n)|\beta$

Dimostrazione:

Sia $\overline{x}$ una soluzione, questo significa che $a\overline{x}=b$, quindi sostituendo $\overline{a}\cdot \overline{x}=\overline{\beta }$ e questo significa che $\alpha x-\beta =nk\exists k\in \mathbb{Z}$. Se spostiamo i membri possiamo scrivere $\alpha x-nk=\beta$ e questo implica che $\beta \in \alpha \mathbb{Z}+n\mathbb{Z}$, notiamo che $\alpha \mathbb{Z}+n\mathbb{Z}=\delta \mathbb{Z}$ dove $\delta =MCD(\alpha ,n)$ e quindi possiamo scrivere che $\delta |\beta$ e questo dimostra che se ammette soluzioni allora $MCD(\alpha ,n)|\beta$.

Adesso dimostriamola nel senso opposto.

Supponiamo quindi che $\delta =MCD(\alpha ,n)|\beta$ quindi possiamo scrivere che $\beta =\delta x$ e questo significa che $\beta \in \alpha \mathbb{Z}+n\mathbb{Z}\iff \exists u,v\in \mathbb{Z}t.c.\beta =u\alpha +vn\iff (\text{Riduzione modulo n})\beta \equiv u\alpha (modn.)\iff \overline{\beta }=\overline{u}\overline{\alpha }$. Possiamo chiamare $\overline{u}=x$ e abbiamo trovato la soluzione.

---

Esempio

L’equazione $\overline{3}\cdot x=\overline{0}$ in $A=\mathbb{Z}/6\mathbb{Z}$ quindi abbiamo che $\alpha =3,\beta =0,n=6$ e $MCD(\alpha ,6)=3|\beta$ e quindi ci sono soluzioni: $x=\overline{2},x=\overline{4},x=\overline{0}$, questo è l’insieme delle soluzioni.

Lemma

Prendiamo $a,b,c\in \mathbb{Z}$ se $a,b|c$ e $MCD(a,b)=1$ allora $ab|c$.

Dimostrazione

Sappiamo che $a,b|c\iff c=ak=bh$ ma questo vuol anche dire che $ak=bh$ e quindi $a|bh$. Notiamo che se $MCD(a,b)=1$ allora implica che $a|h$ e quindi $ab|c$, mostriamolo.

$MCD(a,b)=1\iff b\text{ eˋ invertibile modulo a}\Rightarrow \exists b^{\prime }t.c.b{b}^{\prime }\in 1+a\mathbb{Z}$ (equivalente a dire che $b{b}^{\prime }$ appartiene alla classe di 1 modulo $a$).

Possiamo dire che $a|bh\Rightarrow a{b}^{\prime }|\underset{(1+ak)\cdot h\exists k\in \mathbb{Z}}{\underbrace{b\cdot b^{\prime }\cdot h}}$ adesso facendo un po’ di manipolazioni:

$$\begin{array}{rl}& a{b}^{\prime }=h+ahk\\ & a{b}^{\prime }-ahk=h\\ & a(b^{\prime }-hk)=h\Rightarrow a|h\end{array}$$

---

Teorema Cinese dei Resti

È un modo di risoluzione di sistemi di equazioni lineari a coefficienti interi, queste equazioni sono di tipo congruenziale.

Prendiamo $r_1,\dots ,r_s\in {\mathbb{N}}^{\ast }$ e supponiamo che $MCD(r_i,r_j=1)\forall i\ne j$ quindi sono 2 a 2 primi fra loro. Inoltre consideriamo degli interi $c_1,\dots ,c_s\in \mathbb{Z}$, allora il sistema di congruenze:

$$\ast \{\begin{array}{l}X\equiv c_1\text{mod }{r}_1\\ X\equiv c_2\text{mod }{r}_2\\ \dots \\ X\equiv c_s\text{mod }{r}_s\end{array}$$

Questo sistema ha un’unica soluzione modulo $R:=r_1\cdot ...\cdot r_s$. Ovvero, l’insieme ${\mathcal{E}}_{\ast }=\{x\text{ soluzione in }\mathbb{Z}\text{ di *}\}$ è della forma $x_0+\mathbb{Z}R$. Ricordiamo che abbiamo $X$ indeterminata che è una sola e abbiamo $s$ equazioni congruenziali.

Calcoliamo una soluzione particolare $x_0$ del sistema.

Poniamo $R_i:=\frac{R}{r_i}=r_1\cdot ...\cdot \cancel{r_i}\cdot ...\cdot r_s$ ovvero il prodotto fra tutti gli $r$ senza $r_i$, notare che $MCD(R_i,r_i)=1$ questo vuol dire che $\overline{R_i}$ con $R_i\in \mathbb{Z}/r_i\mathbb{Z}$ è invertibile, ovvero $\exists \overline{S_i}\in \mathbb{Z}/r_i\mathbb{Z}t.c.\overline{R_i}\cdot \overline{S_i}=\overline{1}$ allora questo implica che moltiplicando possiamo scrivere $\overline{R_i}\cdot \underset{=:\overline{y_i}\in \mathbb{Z}/r_i\mathbb{Z}}{\underbrace{\overline{S_i}\cdot \overline{c_i}}}=\overline{c_i}$, in questo modo abbiamo costruito elementi $\overline{y_i},\dots ,\overline{y_s}$ ciascuno in $\mathbb{Z}/r_{i\mathbb{Z}}$.

Dimostriamo che $x_0=\sum _{i=1}^s{y}_i{R}_i\in \mathbb{Z}$ è soluzione di $\ast$.

Se $i\ne j$ allora abbiamo che $r_i|R_j$ quindi $x_0=\sum _{j=1}^s{y}_j{R}_j$ e siccome $R_j$ è divisibile da tutti gli $r_i$ che sono diversi da $r_j$ possiamo scrivere $x_0=\underset{\equiv 0\text{ mod }{r}_i}{\underbrace{\sum _{j=1,j\ne i}^s{y}_j{R}_j}}+y_i{R}_i\equiv y_i{R}_i\text{ mod }{r}_i\equiv c_i\text{ mod }{r}_i$ e questo è valido $\forall i=1,\dots ,s$. Dunque $x_0=\sum _j{y}_j{R}_j$ è una soluzione particolare del nostro sistema $\ast$.

Adesso vogliamo trovare tutte le soluzioni e non soltanto una. Sistema Omogeneo Associato

$${\ast }_H\{\begin{array}{l}X\equiv 0\text{mod }{r}_1\\ X\equiv 0\text{mod }{r}_2\\ \dots \\ X\equiv 0\text{mod }{r}_s\end{array}$$

Ovvero $x\equiv 0\text{ mod }{r}_i$ con $i=1,\dots ,s$, quali sono tutte le soluzioni?

$$\begin{array}{rl}& x\equiv 0\text{ mod}{r}_1\iff r_1|x\\ & x\equiv 0\text{ mod}{r}_2\iff r_2|x\\ & \text{Ma }{r}_{1}e{r}_2\text{ sono primi fra loro quindi (lemma) }{r}_1{r}_2|x\\ & x\equiv 0\text{ mod}{r}_3\iff r_3|x\\ & \text{Ma }MCD(r_3,r_1,r_2)=1\Rightarrow r_1\cdot r_2\cdot r_3|x\\ & \text{Iterando fino a }{r}_s\to R:=r_1\cdots r_s|x\end{array}$$

Le soluzioni di questo sistema quindi sono tutti i multipli di $R$ e quindi $R\mathbb{Z}$. Scriviamolo:

L’insieme delle soluzioni ${\mathcal{E}}_H:=R\mathbb{Z}$, concludiamo con la proposizione: L’insieme delle soluzioni di $\ast$ denotato ${\mathcal{E}}_{\ast }$ è dato da $x_0+R\mathbb{Z}$ ovvero il “traslato” dell’insieme di tutti i multipli di $R$ appunto traslato dalla soluzioni particolare $x_0$, dimostriamolo.

Dimostrazione:

$x_0+R\mathbb{Z}$ è contenuto nell’insieme delle soluzioni, infatti se $x\in x_0+R\mathbb{Z}$ allora posso scrivere $x=x_0+Rk,\exists k\in \mathbb{Z}$ ma $Rk\equiv 0$ mod $r_i$ $\forall i=1,\dots ,s$ infatti $r_i|Rk$ e addizionando con $x_0$ che è soluzione particolare ottengo che $x\equiv c_i+0\equiv c_i$ mod $r_i$.

Dimostriamo adesso che l’insieme delle soluzioni è contenuto in $x_0+R\mathbb{Z}$, sia $x$ una soluzione di $\ast$, allora $x-x_0\equiv 0$ mod $r_i$ $\forall i=1,\dots ,s$ e questo vuol dire che $x-x_0\in R\mathbb{Z}(lemma)$, questo implica che $x\in x_0+R\mathbb{Z}\Rightarrow {\mathcal{E}}_{\ast }\subset x_0+R\mathbb{Z}$.

We’re so cooked :’(

Esercizio 8

Trovare le indeterminate.

$(i)4x\equiv 7(mod.15)$

Dato che $MCD(4,15)=1$ allora significa che $\overline{4}$ è invertibile e quindi $\exists n\in \mathbb{Z}$ tale che $4n\equiv 1(mod.15)$, ad esempio $n=4$.

Quindi moltiplicando $4$ termine a termine otteniamo $4\cdot 4\cdot x\equiv 28(mod.15)$ siccome $4\cdot 4$ ci darà resto 1 possiamo toglierlo e ottenere $x\equiv 13(mod.15)$ che è congruente alla congruenza iniziale, possiamo quindi dire che l’insieme delle soluzioni $\mathcal{E}=15\mathbb{Z}+13$.

$(ii)$ $6x\equiv 8(mod.9)$

Possiamo scrivere quindi che $6x-8=9k$ per un certo $k$ intero e spostando i termini otteniamo $8=6x-9k$. Dato che $MCD(6,9)=3$ e quindi che $3|6x$ e $3|9k$, implica che $3|8$ ma è impossibile e quindi l’insieme delle soluzioni $\mathcal{E}=\varnothing$

$(iii)$ Sistema

$$\{\begin{array}{l}1025x\equiv 5312065(mod.8)\\ 36x\equiv 322(mod.5)\\ 4x\equiv 7(mod.3)\end{array}$$

Abbiamo che $r_1=8,r_2=5,r_3=3$ che sono tutti primi fra loro. Riduciamo nei rispettivi moduli i vari coefficienti.

$$\begin{array}{rl}& 1025=2^{10}+1=(2^3{)}^3\cdot 2+1\equiv 1(mod.8)\\ & 36=35+1\equiv 1(mod.5)\\ & 4\equiv 1(mod.3)\end{array}$$

Quindi dato che sono tutti congruenti a 1 possiamo toglierli dal sistema e semplificarlo in:

$$\{\begin{array}{l}x\equiv 5312065(mod.8)\\ x\equiv 322(mod.5)\\ x\equiv 7(mod.3)\end{array}$$

Adesso passiamo a semplificare i resti:

$$\begin{array}{rl}& 53120658|4\cdot 10^6\Rightarrow 5312065{\equiv }_{8}1312065\\ & 8|1200000\Rightarrow 1312065{\equiv }_{8}112065\\ & 8|120000\Rightarrow 112065{\equiv }_8-7935\\ & 8|8000\Rightarrow -7935{\equiv }_{8}65{\equiv }_{8}1\end{array}$$

Per gli altri valori è più semplice infatti:

$$\begin{array}{rl}& 322{\equiv }_5-3{\equiv }_{5}2\\ & 7{\equiv }_{3}1\end{array}$$

Quindi possiamo riscrivere il nostro sistema nel seguente modo:

$$\{\begin{array}{l}x\equiv 1(mod.8)\\ x\equiv 2(mod.5)\\ x\equiv 1(mod.3)\end{array}$$

E applicare il Teorema Cinese dei Resti quindi denominiamo $c_1=1,c_2=2,c_3=1$ e $r_1=8,r_2=5,r_3=3$ poi scriviamo $R=3\cdot 5\cdot 8=120$ e inoltre $R_1=5\cdot 3=15,R_2=8\cdot 3=24,R_3=8\cdot 5=40$.

Calcoliamo gli inversi:

$$\begin{array}{r}{R}_1\text{ invertibile mod }{r}_1\to S_1=7(15{\equiv }_{8}7)\\ R_2\text{ invertibile mod }{r}_2\to S_2=4(24{\equiv }_{5}4)\\ R_3\text{ invertibile mod }{r}_3\to S_3=1(40{\equiv }_{3}1)\end{array}$$

Adesso calcoliamo i vari $y_i=S_i{c}_i$ che utilizziamo per calcolare $x_0$

$$x_0=\sum _{i=1}^3{y}_i{R}_i=7\cdot 15+3\cdot 24+1\cdot 40=217$$

Quindi la soluzione generale del sistema è data da $x_0+R\mathbb{Z}=217+120\mathbb{Z}$ e possiamo scrivere $\mathcal{E}=97+120\mathbb{Z}$. (97 = 217-120 anche se non ho ben capito perché lo abbiamo fatto ma credo perché sia resto (?))

Polinomi in una Indeterminata a Coefficienti in un Campo

Dato un $K$ campo, abbiamo un polinomio in $X$ a coefficienti in $K$ nella forma:

$$P=\sum _{i=0}^n{a}_i{X}^i$$

Dove $i$ coefficienti con $a_i\in K$ mentre $n$ è un intero che dipende dal polinomio.

Ad esempio possiamo prendere $3x^2+2x+1$ con $K=\mathbb{R}$. Oppure con $K={\mathbb{F}}_2$ abbiamo $\overline{1}{x}^5+\overline{0}{x}^4+\overline{2}{x}^3+\overline{6}{x}^2+\overline{1}x+\overline{1}$ che dato che siamo in modulo 2 possiamo scriverlo anche $x^5+x+\overline{1}$.

---

Possiamo scrivere $A=K[X]$ come l’insieme dei polinomi dove ogni $P\in A$ è definito come:

$$P=\sum _{i\ge 0}{a}_i{X}^i{a}_i=0\forall i\gg 0$$

Con $\gg$ intendiamo per ogni $i$ abbastanza grande il coefficiente diventa 0, ovvero fino ad un certo punto avremo dei valori non nulli e poi sempre 0.

Possiamo appunto notare che c’è una struttura ad anello, definiamo quindi le operazioni di somma e moltiplicazione.

Abbiamo i due polinomi:

$$\begin{array}{r}P=\sum _{i\ge 0}{a}_i{X}^i{a}_i=0\forall i\gg 0\\ Q=\sum _{i\ge 0}{b}_i{X}^i{b}_i=0\forall i\gg 0\end{array}$$

Possiamo scrivere la somma come:

$$P+Q:=\sum _{i\ge 0}(a_i+b_i)X^i$$

Mentre per la moltiplicazione:

$$P\cdot Q=\sum _{k\ge 0}{c}_k{X}^k\text{dove }{c}_k=\underset{\text{Formula Cauchy}}{\underbrace{\sum _{i+j=k}{a}_i{b}_j}}$$

Si nota che $c_k=0$ per ogni $k$ abbastanza grande perché avremo che $a_i$ oppure $b_j$ nullo.

Possiamo quindi definire l’anello $(A,-,+,\cdot ,0,1)$

Grado di un Polinomio

Prendiamo un polinomio $P\in A[X]$ e quindi definito come $P=\sum _{i{\ge }_0}{a}_i{X}^i$ con $a_i=0\forall i\gg 0$ e inoltre $P\ne 0\{j\in \mathbb{N}t.c.a_j\ne 0\}$ ovvero finito non vuoto.

$deg(P)=max\{j\in \mathbb{N}{a}_j\ne 0\}$ (credo con j intenda i (?)).

Grado di P

Si pone per definizione $deg(0)=-\infty$ e quindi l’insieme dei gradi possibili è dato da $\mathbb{N}\bigsqcup \{-\infty \}$.

Esempio

$\{P\in K[X]:deg(P)=0\}=K^X$

Applicazione deg

La funzione $deg$ è definita $\underset{A}{\underbrace{K[X]}}\to \mathbb{N}\bigsqcup \{-\infty \}$

Lemma: Dati $a,b\in A$ abbiamo 3 proposizioni:

1. $deg(a)=-\infty \iff a=0$
2. $deg(ab)=deg(a)+deg(b)$
3. $deg(a+b)\le max(deg(a),deg(b))$ e per l’uguaglianza nello specifico: $deg(a+b)=max(deg(a),deg(b))\iff deg(a)\ne deg(b)$

Esempi

$a=x^2+x+1$ e $b=x+1$ abbiamo che $deg(a+b)=2=max(1,2)$ e infatti $deg(a)\ne deg(b)$

$a=x^5+6x-3$ e $b=-x^5+4x^2+2x-1$ dato che $a+b=4x^2+8x-4$ abbiamo che $deg(a+b)=2<max(5,5)$

Casi Particolari

In alcuni casi può comunque capitare che $deg(a)=deg(b)=d$ e $deg(a+b)=d$

Analogia tra Interi e Polinomi

Vedremo che tutti gli enunciati visti per gli interi valgono anche sui polinomi, per alcuni di questi vedremo anche le loro dimostrazioni mentre altri li prenderemo per giusti.

Valore Assoluto

Su $\mathbb{Z}$ abbiamo l’applicazione valore assoluto: $\mathbb{Z}\stackrel{|\cdot |}{\to }\mathbb{N}$, questa soddisfa alcune proprietà:

1. $|a|=0\iff a=0$
2. $|ab|=|a|\cdot |b|$ - Compatibilità con la moltiplicazione
3. $|a+b|\le |a|+|b|$ - Disuguaglianza Triangolare Invece su $A$ (anello di polinomi) abbiamo visto il grado: $A\stackrel{deg}{\to }\mathbb{N}\bigsqcup \{-\infty \}$, queste soddisfa:
4. $deg(a)=-\infty \iff a=0$
5. $deg(ab)=deg(a)+deg(b)$
6. $deg(a+b)\le max(deg(a),deg(b))$

Notiamo che ci sono delle somiglianze, ma ci serve un’altra struttura per rendere queste operazioni ancora più simili e avere quindi un valore assoluto anche sui polinomi.

Scegliamo un numero reale $c>1$, poi dato un polinomio $P\in A\backslash \{0\}$ definiamo:

$$|P{|}_c:=c^{deg(P)}\text{ Valore assoluto di P relativo a c (dipende da c)}$$

Poniamo anche $|0{|}_c:=0$ che non è altro che $c^{-\infty }$, questa è una nostra convenzione.

Allora le 3 proprietà viste prima sono equivalenti a:

1. $|a{|}_c=0\iff a=0$
2. $|a\cdot b{|}_c=|a{|}_c\cdot |b{|}_c$
3. $|a+b{|}_c\le max(|a{|}_c,|b{|}_c)\le |a{|}_c+|b{|}_c$

Vediamo perché 2 funziona:

$|a\cdot b{|}_c=c^{deg(a\cdot b)}=c^{deg(a)+deg(b)}=c^{deg(a)}\cdot c^{deg(b)}=|a{|}_c\cdot |b{|}_c$

Vediamo perché 3 funziona:

$|a+b{|}_c=c^{deg(a+b)}\le c^{max(deg(a),deg(b))}\le c^{deg(a)}+c^{deg(b)}=|a{|}_c+|b{|}_c$

Algoritmo della Divisione Euclidea (per polinomi)

Teorema: Dati $a,b\in A=K[X]$ con $(a,b)\ne (0,0)$:

$$\exists !(q,r)\in A\times At.c.a=q\cdot b+r\text{ dove }\underset{|r{|}_c<|b{|}_c}{\underbrace{deg(r)<deg(b)}}$$

Se usiamo il valore assoluto in relazione a $c$, notiamo che siamo molto vicini alla definizione di divisione euclidea in $\mathbb{Z}$ infatti abbiamo che il resto deve essere strettamente inferiore al divisore ma in questo caso abbiamo il suo grado.

Analogie

Vediamo nel dettaglio le analogie tra $\mathbb{Z}$ e $A=K[X]$.

• In entrambi i casi abbiamo la divisione euclidea.
• In $\mathbb{Z}$ abbiamo il valore assoluto $|\cdot |$ mentre per i polinomi abbiamo $|\cdot {|}_c$ e il grado $deg(\cdot )$.

---

A cosa corrisponde ${\mathbb{N}}^{\ast }$ di $\mathbb{Z}$? Ovvero l’insieme degli interi positivi.

Nei polinomi abbiamo i polinomi monici $A^{+}=\{\text{polinomi monici}\}$, i polinomi monici sono quei polinomi che hanno il coefficiente del termine con grado più alto uguale a 1. In altre parole il termine che rappresenta il grado del polinomio deve avere coefficiente 1.

---

In $\mathbb{Z}$ come elementi invertibili abbiamo ${\mathbb{Z}}^X=\{\pm 1\}$.

Per quanto riguarda $A^X$? Sia $a\in A^X$ allora $\exists b\in A^X$ tale che $ab=1$, adesso calcoliamo il grado da entrambe le parti.

$ab=1\Rightarrow deg(a)+deg(b)=0$ notiamo che $deg(a)$ e $deg(b)$ sono sicuramente in $\mathbb{N}$ infatti non possono essere $-\infty$ altrimenti non otterremmo 0 come risultato. Ma la somma di due interi superiori uguali a 0 è 0 se e solo se sono entrambi 0. Quindi $deg(a)=deg(b)=0$.

Questo implica che $a,b\in K^X$ ovvero che sono due numeri.

Tutto questo significa che $A^X=K^X$ ed è quindi l’analogo di ${\mathbb{Z}}^X$ in $A$.

Ricordiamo che gli elementi invertibili di un campo sono tutti gli elementi tranne zero

---

Per la divisibilità in $\mathbb{Z}$ abbiamo una relazione sugli interi tale che $a|b\iff b=ak\exists k\in \mathbb{Z}$ che è equivalente anche alle scritture:

• $b\in a\mathbb{Z}$
• $b\mathbb{Z}\subset a\mathbb{Z}$

Vediamo cosa succede in $A$:

$a|b\iff \exists H\in At.c.b=aH$ che è equivalente alle scritture:

• $b\in aA=\{al:l\in A\}$
• $bA\subset aA$

Proprietà della divisibilità di polinomi

• Riflessiva dato che ogni polinomio divide se stesso
• Transitiva: Se abbiamo $a|b$ e $b|c$ è equivalente a dire $cA\subset bA\subset aA\Rightarrow cA\subset aA\Rightarrow a|c$.

---

Esercizio

Prendiamo $a,b\in A\backslash \{0\}$ e supponiamo che $a|b\wedge b|a$ questo equivale a dire:

• $\exists U\in At.c.b=aU$
• $\exists V\in At.c.a=bV$ Adesso se sostituiamo: $a=UVa$ e calcoliamo il grado:

$$deg(a)=deg(a)+deg(U)+deg(V)\to 0=deg(U)+deg(V)$$

Questo significa, come visto prima, $deg(U)=deg(V)=0$ e quindi significa che i miei polinomi sono $U=\lambda \in K^X$ e $V=\mu \in K^X$

Abbiamo dimostrato quindi che $\exists \lambda \in K^X=A^X$ tale che $b=\lambda a$ che è analogo a quello che abbiamo visto in $\mathbb{Z}$ ovvero:

$$a,bt.c.a|b\wedge b|a\Rightarrow \exists \lambda \in {\mathbb{Z}}^{X}t.c.b=\lambda a$$

---

Lemma: $A=K[X]$ è un dominio d’integrità (non ha divisori di zero escluso zero).

Dimostrazione:

Sia $P\in A$ un divisore di zero allora $\exists Q\in A\backslash \{0\}$ tale che $PQ=0$, calcoliamo i gradi.

$$deg(PQ)=deg(P)+deg(Q)=deg(0)\Rightarrow deg(P)+deg(Q)=-\infty$$

Però sappiamo che $Q$ non è nullo e quindi non può avere grado $-\infty$, questo significa che è $P$ ad avere grado $-\infty$, questo grado implica che $P=0$

Congruenze con i Polinomi

In $\mathbb{Z}$ abbiamo che $a{\equiv }_{n}b\iff n|a-b$ e questo porta ad una struttura di anello che si scrive $\mathbb{Z}/n\mathbb{Z}$ e gli elementi di questo anello sono le classi di equivalenza che sono dei traslati per degli interi di tutti i multipli di $n$, quindi ad esempio se $a\in \mathbb{Z}$ allora $[a]:=a+n\mathbb{Z}$.

Per $A$ cosa possiamo dire?

Prendiamo $a,b\in A$ e $H\in A\backslash \{0\}$. Diciamo che $a{\equiv }_{H}b$ e questo è equivalente alle congruenze in $\mathbb{Z}$, proviamo a osservare la transitività.

Supponiamo quindi che $a{\equiv }_{H}b$ e $b{\equiv }_{H}c$ quindi questo significa che $H|a-b$ e $H|b-c$. Inoltre possiamo dire che $a-b=HU$ per un certo $U$ e $b-c=HV$ per un certo $V$. Addizioniamo termine a termine:

$$a-b+b-c=H(U+V)\to a-c=H(U+V)\iff H|a-c\iff a{\equiv }_{H}c$$

Quindi troviamo l’anello $A/HA$ e notiamo che la congruenza è compatibili con le varie operazioni come in $\mathbb{Z}$. Quindi ad esempio $[a]=a+HA$ che è anche $\subset A$.

---

Quindi $A/HA=\{[a]:a\in A\}$, però vogliamo trovare un SCR modulo H, quindi scriviamo l’insieme di prima come $A/HA=\{a+HA:a\in At.c.deg(a)<deg(H)\}$ e notiamo che l’insieme $\{a\in A:deg(a)<deg(H)\}$ è un SCR per la congruenza modulo H.

Massimo Comun Divisore

Dati $a,b\in A$ poniamo $aA+bA=\{m\in A:\exists u,v\in A\text{ con }m=ua+vb\}$ è valido quindi il lemma di Bezout.

Lemma: Dati $a,b\in A$ supponiamo che $(a,b)\ne (0,0)$ e allora $aA+bA=\delta A$ con $\exists !\delta \in A^{+}$ (monico).

Confrontiamo i due insiemi.

Su $\mathbb{Z}$ abbiamo per definire MCD abbiamo $(a,b)\in {\mathbb{Z}}^2\backslash \{(0,0)\}$ deve $\exists !d\in {\mathbb{N}}^{\ast }$ tale che:

• $d|a\wedge d|b$
• Se $d^{\prime }\in \mathbb{Z}$ tale che $d^{\prime }|a\wedge d^{\prime }|b$ allora $d^{\prime }|d$

Su $A$ prendiamo $(a,b)\in A^2\backslash \{(0,0)\}$ e abbiamo che $\exists !d\in A^{+}$ (monico) tale che:

• $d|a\wedge d|b$
• Se $d^{\prime }\in A$ tale che $d^{\prime }|a\wedge d^{\prime }|b$ allora $d^{\prime }|d$

Inoltre in entrambi i casi possiamo scrivere $MCD(a,b)=d=\delta$.

Polinomi primi fra loro

Si dice che $a,b\in A$ sono primi fra loro se $MCD(a,b)=1$ come accade su $\mathbb{Z}$. Anche qui funziona il calcolo del massimo comun divisore con l’algoritmo euclideo.

Polinomi Irriducibili

Prendiamo $P\in A\backslash A^X(deg(P)>0)$ si dice che $P$ è irriducibile se scrivendo una fattorizzazione di $P$ come prodotto tra due polinomi $Q$ ed $R$ con almeno uno grado 0, quindi $P=QR$ si ha che o $Q\in K^X$ oppure $R\in K^X$.

Polinomi Primi

Prendiamo sempre un $P\in A\backslash A^X$, $P$ si dice primo se quando $P|QR$ allora o $P|Q$ o $P|R$.

Inoltre abbiamo un lemma: $\text{P irriducibile}\iff \text{P primo}$.

---

Quindi se prendiamo l’anello $A/PA$ con $P$ irriducibile, è un campo.

Teorema Fattorizzazione Unica (T.F.A.)

Ogni $H\in A\backslash \{0\}$ si decompone in modo unico come prodotto:

$$H=\underset{\in A^X}{\lambda }\cdot \prod _{P\in A^{+}\text{ e irriducibile}}{P}^{v_p(H)}$$

Dove $v_p(H)\in \mathbb{N}$ e $\{Pt.c.v_p(H){\ne }_0\}$ è un insieme finito. È quindi uguale all’enunciato di $\mathbb{Z}$.

Questa fattorizzazione è facile in $K=\mathbb{R},\mathbb{C}$:

In $\mathbb{C}[X]$ i polinomi monici e irriducibili sono tutti i polinomi nella forma:

$$X-\alpha :\alpha \in \mathbb{C}$$

Quindi su $\mathbb{C}$ i polinomi irriducibili sono tutti i polinomi di grado 1.

Mentre in $\mathbb{R}[X]$ se $P$ è monico e irriducibile allora si ha una delle due proprietà:

• $deg(P)=1$ e quindi come prima $P=X-\alpha :\alpha \in \mathbb{R}$
• $deg(P)=2$ e quindi quando scriviamo $P=X^2+aX+b$ deve accadere $\Delta =a^2-4b<0$

---

La fattorizzazione è più difficile in ${\mathbb{F}}_p,\mathbb{Q}$ perché non c’è un algoritmo che permette di scrivere la lista dei polinomi irriducibili monici. Questo soprattutto per $\mathbb{Q}$.

Valutazione

Prendiamo $x\in K$ e $F\in K[X]$, con $F=F_0,F_1,X+\cdots +F_n{X}^n$ la valutazione di $F$ in $x$ è:

$$e{v}_x(F):=F_0+F_{1}x+\cdots +F_n{x}^n$$

Quindi abbiamo $e{v}_x:K[X]\to K$, infatti sostituiamo il valore dell’indeterminata e abbiamo una somma fra valori. Questa operazione di valutazione è compatibili con le operazioni di addizione e moltiplicazione.

Osservazione

1. $e{v}_x(F+G)=e{v}_x(F)+e{v}_x(G)$
2. $e{v}_x(FG)=e{v}_x(F)\cdot e{v}_x(G)$
3. $\lambda \in K,e{v}_x(\lambda )=\lambda$

Si dice che $e{v}_x:K[X]\to K$ è un morfismo di anelli (lo vedremo sui gruppi, per ora non serve molto).

Esempio

Prendiamo $F=X^2+1\in \mathbb{R}[X]$ e $x=1$ allora:

$$e{v}_x(F)=x^2+1=2$$

---

Lemma: Sia $x\in K$ allora $e{v}_x^{-1}(\{0\})=\{P\in At.c.e{v}_x(P)=0\}=(X-x)A$. L’immagine inversa di 0 è l’insieme di tutti gli $x\in K$ tali che se li sostituiamo nel polinomio, questo ci da 0. È quindi l’insieme dei polinomi che si annullano in $x$.

Dimostrazione: Dobbiamo dimostrare che i due insiemi sono uno incluso nell’altro.

Mostriamo che $(X-x)A\subset \{P\in At.c.e{v}_x(P)=0\}$ ovvero dimostrare che ogni multiplo di $(X-x)$ ha la proprietà che $e{v}_x=0$.

Sia $Q=(X-x)H$ allora $e{v}_x(Q)=\underset{x-x=0}{\underbrace{e{v}_x(X-x)}}\cdot e{v}_x(H)=0\Rightarrow Q\in e{v}_x^{-1}(\{0\})$

Mostriamo l’inclusione inversa

Sia $P\in A$ tale che $v{p}_x(P)=0$. Applichiamo l’algoritmo della divisione euclidea per il polinomio $(X-x)$ quindi:

$$\exists !(q,r)\in A\times At.c.P=q\stackrel{b}{\overbrace{(X-x)}}+r$$

E per il grado di $r$ abbiamo due possibilità $deg(r)\in \{-\infty ,0\}$ dato che $b$ è di grado 1 e quindi il grado di $r$ deve essere strettamente minore. Questo è equivalente a dire che $r\in K$ perché è o 0 o un elemento non nullo.

Adesso valutiamo entrambe le parti:

$$\begin{array}{rl}\stackrel{0}{\overbrace{e{v}_x(P)}}& =e{v}_x(q(X-x)+r)\\ & =e{v}_x(q)\cdot \underset{0}{\underbrace{e{v}_x(X-x)}}+e{v}_x(r)\Rightarrow e{v}_x(r)=0\end{array}$$

Quindi $r$ si annulla in $x$, però sappiamo che $r\in K$ inoltre sappiamo che $e{v}_x(\lambda )$ con $\lambda \in K$ è uguale a $\lambda$ stesso e quindi $e{v}_x(r)=0\Rightarrow r=0$

Quindi se $r=0$ significa che $(X-x)|P$ e questo è equivalente a dire che $P\in (X-x)A$.

Possiamo dire che $P$ ha una radice in $x\iff X-x|P$ che significa $e{v}_x(P)=0$.

Osservazione

Se prendiamo $X-x$ polinomio è sempre irriducibile (e quindi anche primo) $\forall x\in K$ perché:

$$X-x=U\cdot V$$

Calcolando i gradi:

$$\stackrel{1}{\overbrace{deg(X-x)}}=deg(U)+deg(V)$$

Questo implica che $\{deg(U),deg(V)\}=\{0,1\}$ dato che non possono essere $-\infty$, e quindi uno dei due è invertibile ovvero che $\{U,V\}\cap A^X\ne \varnothing$.

---

Esercizi sulla fattorizzazione di polinomi

Esercizio

$X^2+X+6$ in $\mathbb{R}[X]$

Calcoliamo $\nabla (X^2+X+6)=-23<0$ e quindi dato che negativo il polinomio è irriducibile in $\mathbb{R}[X]$

Esercizio

$X^3-6X^2+11X-6$ in $\mathbb{R}[X]$

Possiamo fare dei tentativi e notare che $1$ è radice del polinomio, ovvero sostituendo $X$ con $1$ otteniamo $0$.

Sappiamo quindi che $x-1$ divide il nostro polinomio, dobbiamo trovare il quoziente della divisione, lo facciamo attraverso la divisione euclidea (non scrivo i passaggi, è la divisione fra polinomi).

Come quoziente otteniamo $X^2-5X+6$ e quindi possiamo scrivere il polinomio come:

$$(X-1)\underset{\text{Ancora scomponibile}}{\underbrace{(X^2-5X+6)}}$$

Possiamo scomporlo in $(X-2)(X-3)$ e quindi alla fine otteniamo come fattorizzazione:

$$(X-1)(X-2)(X-3)$$

In $\mathbb{R}[X]$

Esercizio

$F=X^2-2X+2$ in $\mathbb{C}[X]$ ma osserviamo che $F\in \mathbb{R}[X]\subset \mathbb{C}[X]$, quindi le fattorizzazioni ottenute in $\mathbb{R}[X]$ possiamo mantenerle in $\mathbb{C}[X]$

Notiamo che $\nabla (F)=-4<0$ ed è quindi irriducibile su $\mathbb{R}[X]$ però in $\mathbb{C}[X]$ ammette due radici:

$$X_1=\frac{2+2i}{2}{X}_2=\frac{2-2i}{2}$$

E quindi otteniamo $F=(X-(1+1))(X-(1-i))$

Esercizio

$F=X^3-1$ in $\mathbb{R}[X]$ e $\mathbb{C}[X]$

Osserviamo che $e{v}_1(F)=0$ e quindi in $\mathbb{R}[X]$, svolgendo la divisione otteniamo:

$$F=(X-1)\underset{\text{Irrid. in }\mathbb{R}}{\underbrace{(X^2+X+1)}}$$

Quindi in $\mathbb{R}[X]$ ci fermiamo, ma possiamo continuare su $\mathbb{C}[X]$ con le radici:

$$X_1=\frac{-1-\sqrt{-3}}{2}{X}_2=\frac{-1+\sqrt{-3}}{2}$$

E quindi mantenendo anche $X-1$ abbiamo $F=(X-1)(X-X_1)(X-X_2)$

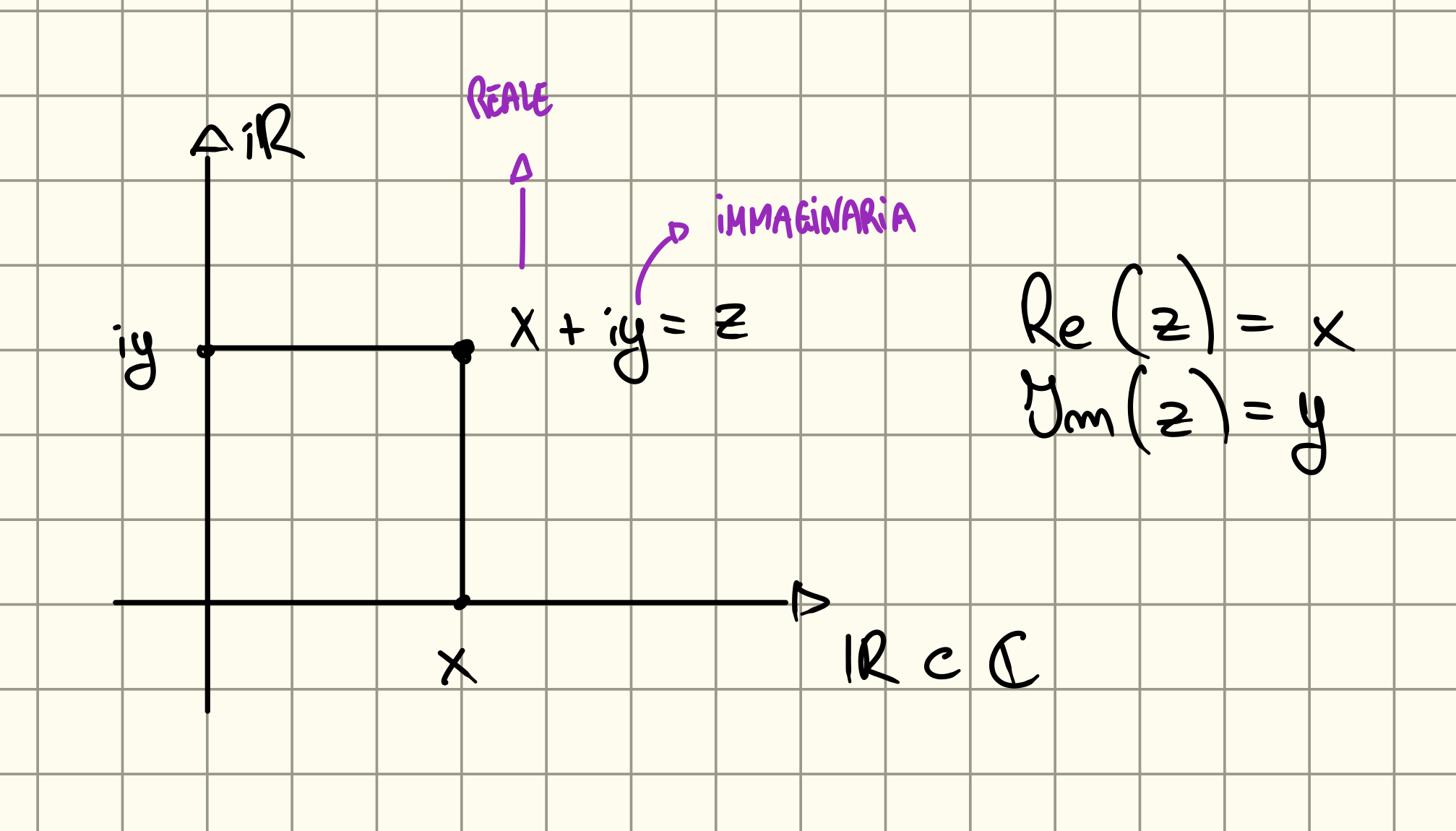
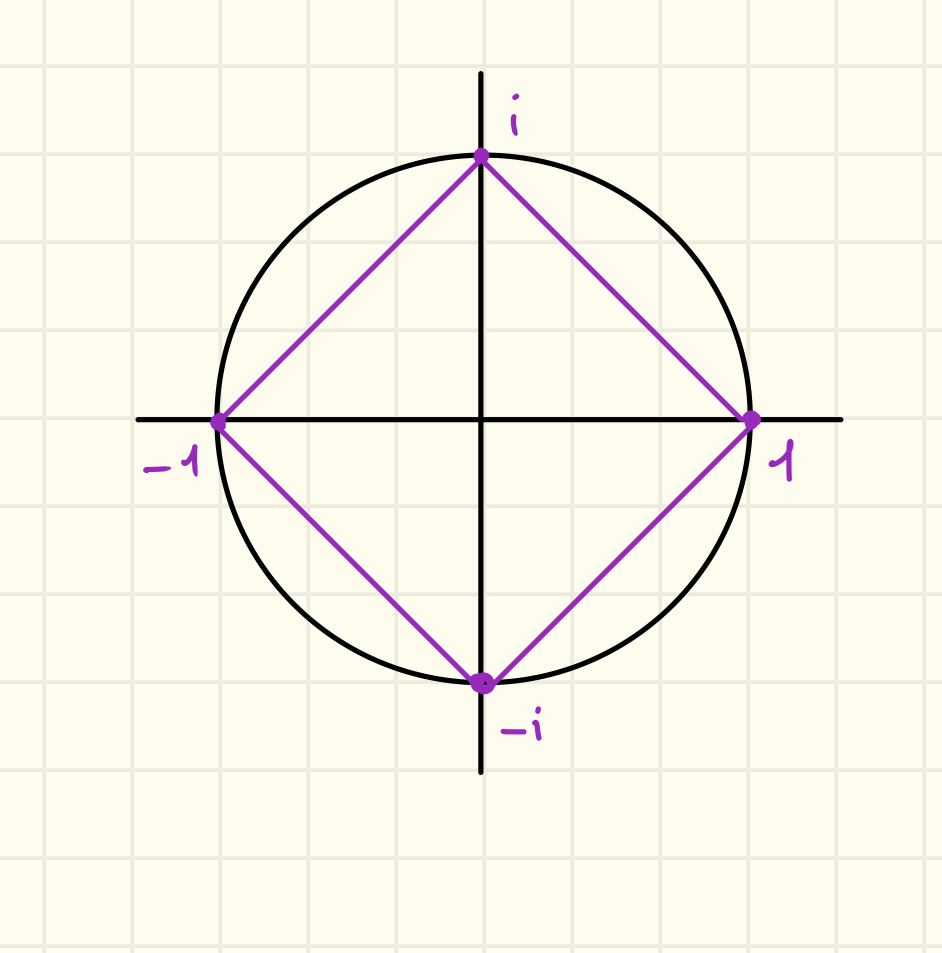
Numeri Complessi

L’insieme dei numeri complessi è definito $\mathbb{C}=\{x+iy:x,y\in \mathbb{R}\}$ dove $i:=\sqrt{-1}$ e quindi $i^2=-1$, possiamo anche dire che $\mathbb{C}=\mathbb{R}+i\mathbb{R}$.

Operazioni sui numeri Complessi:

Definiamo $z=x+iy$ e $z^{\prime }=x^{\prime }+i{y}^{\prime }$ due numeri complessi.

• $-z:=-x+i(-y)$
• $z+z^{\prime }:=(x+x^{\prime })+i(y+y^{\prime })$
• $z\cdot z^{\prime }:=(x+iy)(x^{\prime }+i{y}^{\prime })=x{x}^{\prime }+xi{y}^{\prime }+iy{x}^{\prime }+i^{2}y{y}^{\prime }=x{x}^{\prime }-y{y}^{\prime }+i(y{x}^{\prime }+x{y}^{\prime })$

Quindi $(\mathbb{C},-,+,\cdot ,0,1)$ è un anello

Rappresentazione nel Grafico

Esponenziale di Eulero

$e^{i\sigma }:=\cos \sigma +i\sin \sigma \in \mathbb{C}$ con $\sigma \in \mathbb{R}$.

Eulero ha notato che se $\sigma ,\eta \in \mathbb{R}$:

$$e^{i\sigma }\cdot e^{i\eta }=e^{i(\sigma +\eta )}$$

E in modo simile troviamo anche che $(e^{i\sigma }{)}^n=e^{in\sigma }\forall n\in \mathbb{N}$.

Esempi

• $e^{i2\pi }=\cos (2\pi )+i\sin (2\pi )=1+i0=1$
• $e^{i0}=\cos (0)+i\sin (0)=1+i0=1$
• $1=e^{i2\pi }=e^{\frac{i2\pi }{3}\cdot 3}=(e^{\frac{i2\pi }{3}}{)}^3$

Quindi se poniamo $x=e^{\frac{2\pi i}{3}}$ possiamo dire che $x^3=1$ e quindi $x$ è radice di $x^3-1$ ovvero $e{v}_x(x^3-1)=0$.

Osserviamo che possiamo scrivere:

$$1=1^2=(e^{\frac{2\pi i}{3}}{)}^{3\cdot 2}=(e^{\frac{2\pi i}{3}\cdot 2}{)}^3=(e^{\frac{4\pi i}{3}}{)}^3$$

E quindi anche $x^2$ è radice di $x^3-1$.

Notiamo che:

$$\begin{array}{rl}& x^0=e^{\frac{0\pi i}{3}}=\cos (\frac{0\pi }{3})+i\sin (\frac{0\pi }{3})=1\\ & x^1=e^{\frac{2\pi i}{3}}=\cos (\frac{2\pi }{3})+i\sin (\frac{2\pi }{3})\\ & x^2=e^{\frac{4\pi i}{3}}=\cos (\frac{4\pi }{3})+i\sin (\frac{4\pi }{3})\end{array}$$

L’insieme $\{x^0,x^1,x^2\}=\mathcal{R}$ ha 3 elementi distinti e $\forall y\in \mathcal{R}$ abbiamo che

$$e{v}_y(X^3-1)=0\Rightarrow X^3-1=(X-x^0)(X-x^1)(X-x^2)$$

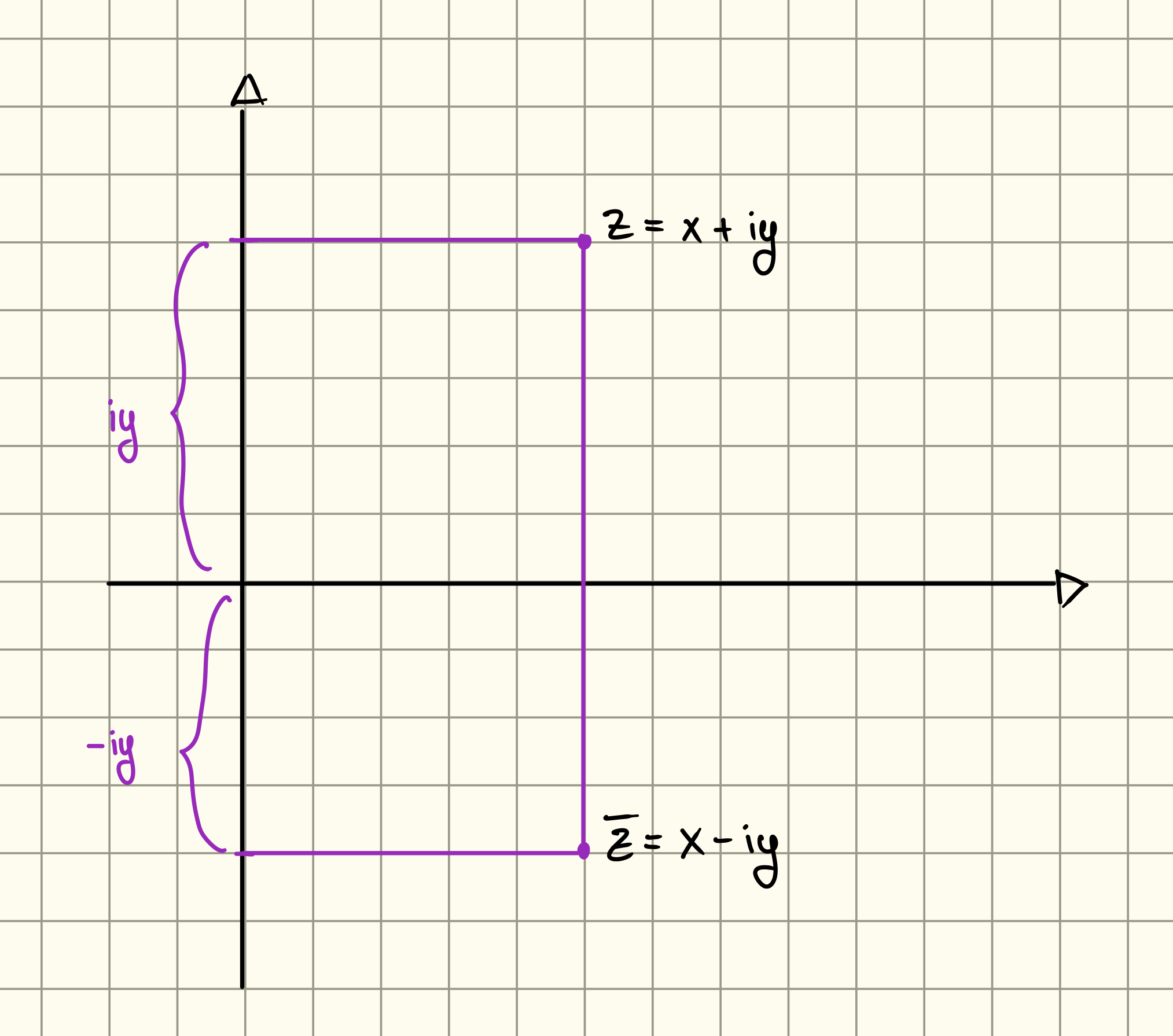
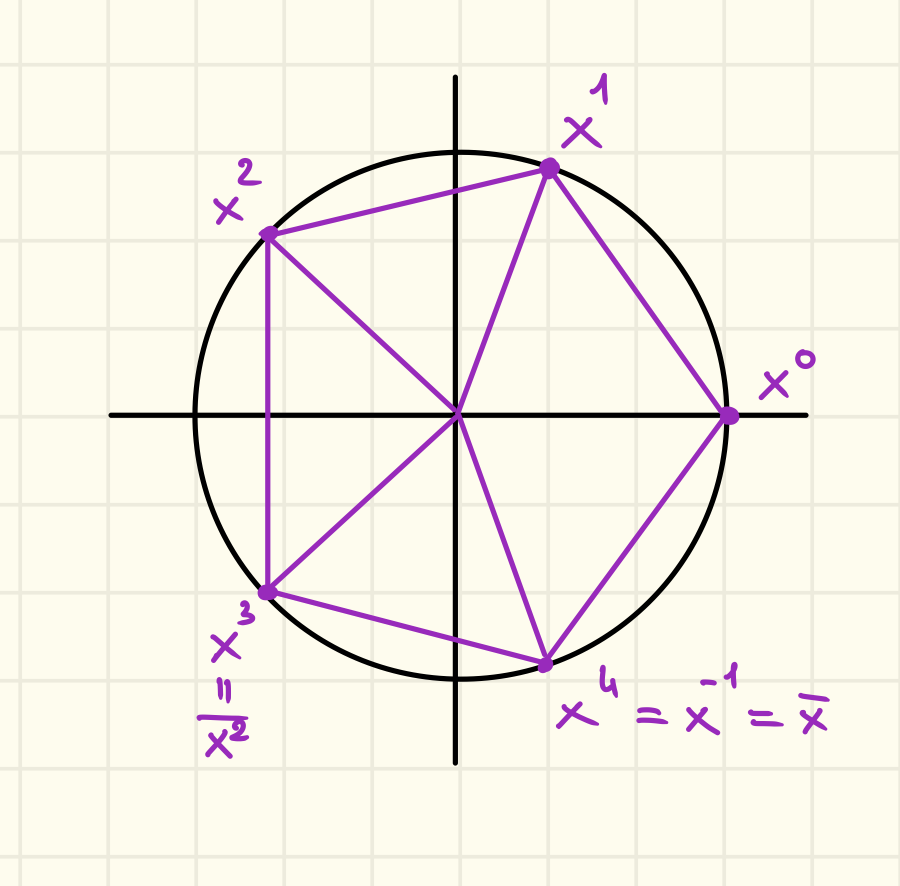
Coniugazione Complessa

Si pone per $z=x+iy\in \mathbb{C},\overline{z}=x-iy\in \mathbb{C}$.

Poniamo anche $h:\mathbb{C}\to \mathbb{C}$ e quindi $h(z):=\overline{z}$.

$\forall z,z^{\prime }\in \mathbb{C}$ si ha:

• $h(z+z^{\prime })=h(z)+h(z^{\prime })$
• $h(z{z}^{\prime })=h(z)h(z^{\prime })$
• $h(-z)=-h(z)$
• $h$ è una biiezione ovvero $h^{-1}=h$

Le formule viste sopra possiamo anche scriverle: $\overline{z+z^{\prime }}=\overline{z}+\overline{z^{\prime }},\overline{z\cdot z^{\prime }}=\overline{z}\cdot \overline{z^{\prime }},ecc\dots$

Quando $h$ rispetta queste proprietà si dice che è un isomorfismo d’anelli ovvero un morfismo invertibile.

Nei reali, abbiamo che $z=\overline{z}$ infatti non hanno parte immaginaria. Graficamente la coniugazione complessa corrisponde alla riflessione rispetto all’asse $\mathbb{R}$:

Formule Fondamentali

• $z\cdot \overline{z}=(x+iy)\cdot (x-iy)=x^2-ixy+ixy+y^2=x^2+y^2$

  Questo è uguale a 0 se e solo se $x=y=0$ mentre è maggiore di 0 se e solo se $z\in \mathbb{C}\backslash \{0\}$

• $|z|=\sqrt{z\overline{z}}=\sqrt{x^2+y^2}$, valore assoluto complesso

---

Dimostriamo che $\mathbb{C}$ è un campo ovvero che ogni elemento non nullo è invertibile.

Dato $z\in \mathbb{C}\backslash \{0\}$, prendiamo $z\overline{z}=x^2+y^2$, che sappiamo essere maggiore di 0 dato che $z$ non è nullo. Lo moltiplichiamo per il suo inverso $(x^2+y^2{)}^{-1}$.

Quindi sappiamo che $z\overline{z}\cdot (x^2+y^2)=1$ dato che è il suo inverso ma possiamo anche dire che:

$$z\cdot \underset{\text{Inverso di z}}{\underbrace{\overline{z}(x^2+y^2{)}^{-1}}}=1$$

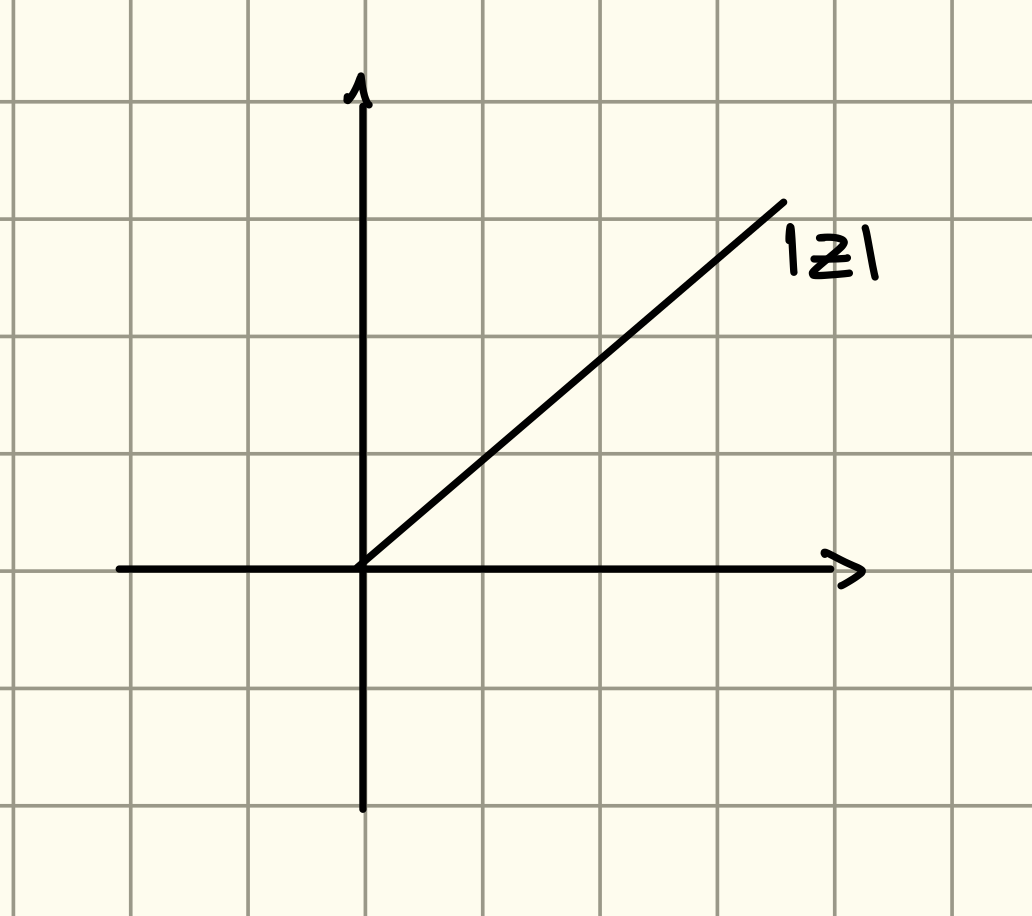
Valore Assoluto Complesso

Graficamente possiamo vederlo come:

Questo ha diverse proprietà:

• $|z|=0\iff z=0$
• $|z{z}^{\prime }|=|z|\cdot |z^{\prime }|$
• $|z+z^{\prime }|\le |z|+|z^{\prime }|$

---

Vediamo altre proprietà e dimostriamole:

$\forall \sigma \in \mathbb{R}$:

• $|e^{i\sigma }|=1$
• $(e^{i\sigma }{)}^{-1}=\overline{e^{i\sigma }}=e^{-i\sigma }$

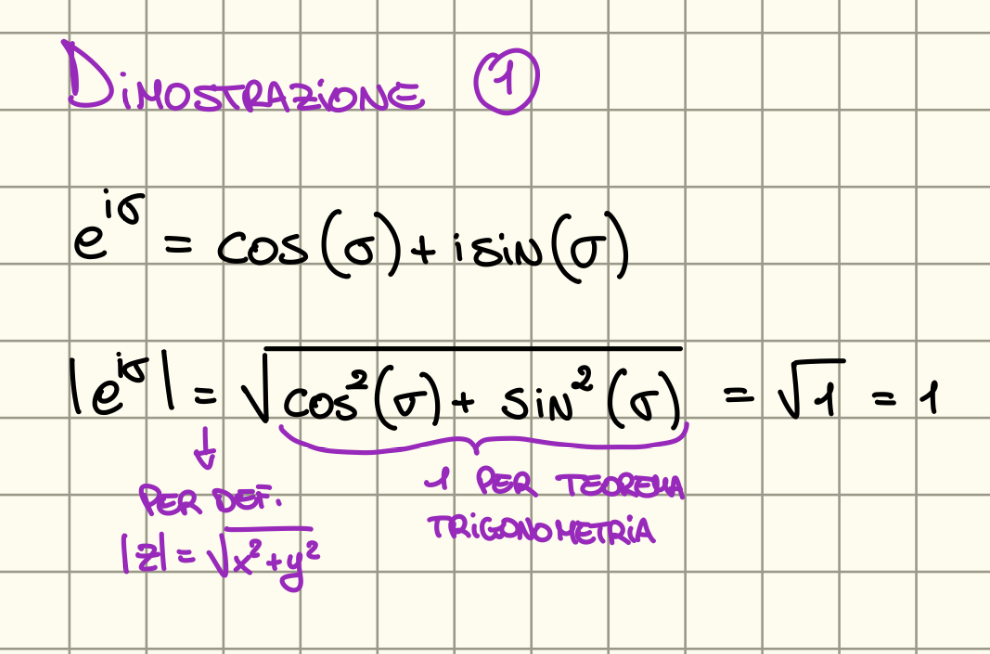
Dimostrazione 2 da finire di controllare su iPad.

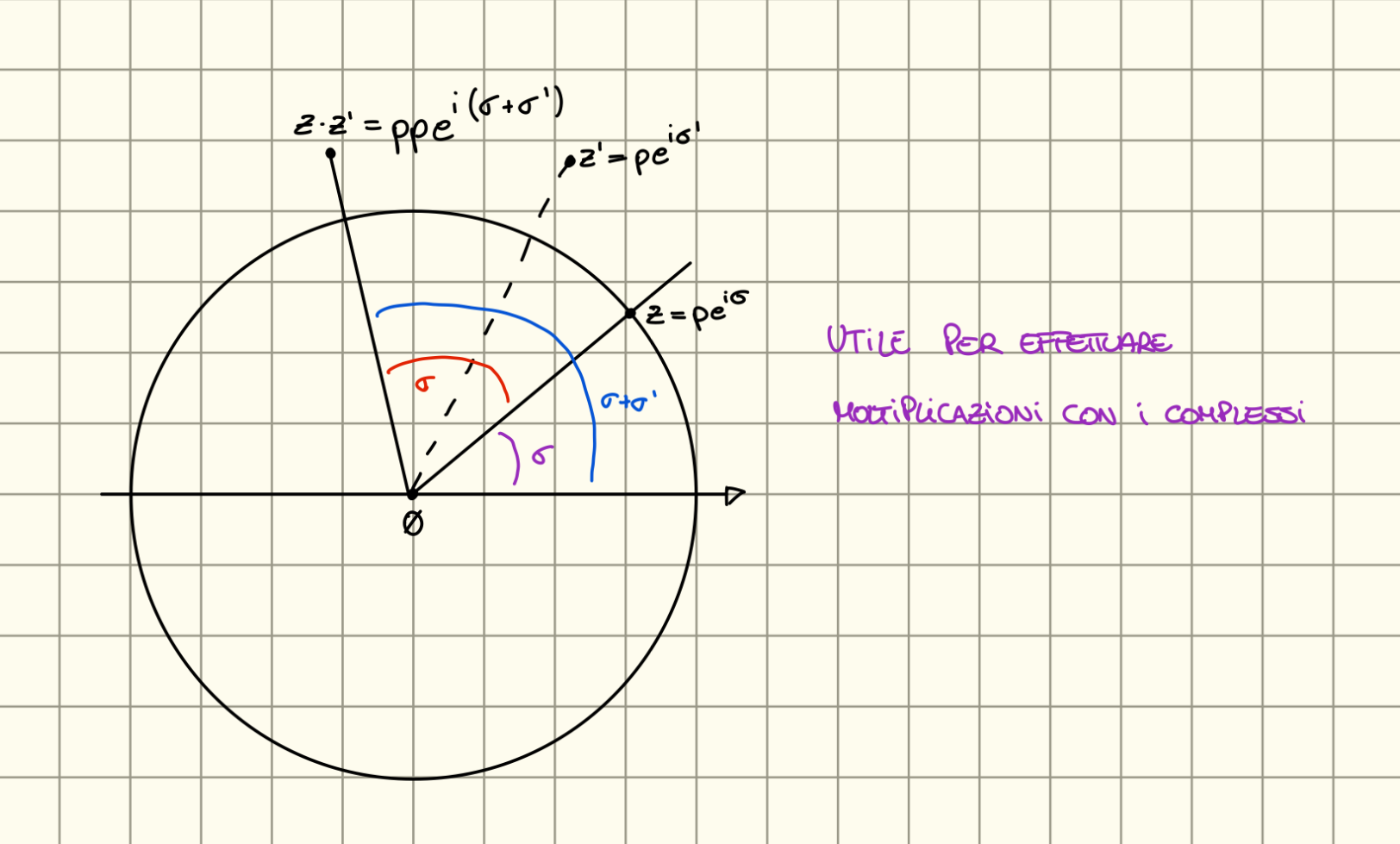
Rappresentazione Polare

Dati $z\in \mathbb{C}$ e $z=x+iy,p=\sqrt{x^2+y^2}$

Lemma

Esiste $\sigma \in \mathbb{R}$ tale che $z=p\cdot e^{i\sigma }$, inoltre $\sigma +2\pi \mathbb{Z}$ è unicamente determinato.

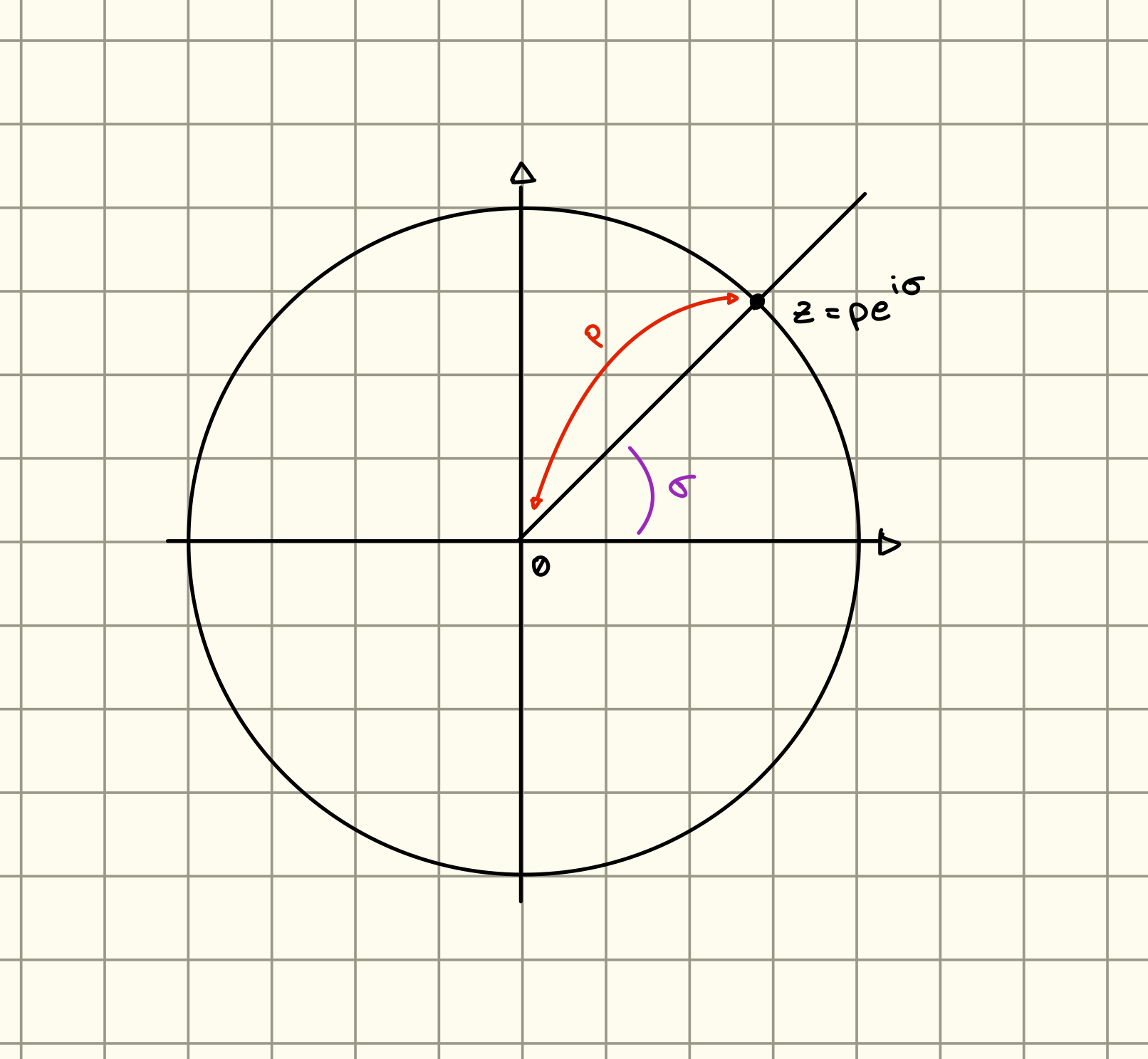
Dimostrazione

Sappiamo che $p=\sqrt{z\overline{z}}$, inoltre definiamo $z^{\prime }:=p^{-1}\cdot z$

• $z^{\prime }\overline{z^{\prime }}=p^{-1}z\cdot \overline{p^{-1}}\overline{z}$ sappiamo che $p$ è reale quindi il suo coniugato è un reale, moltiplicando tutto possiamo scrivere $p^{-2}z\overline{z}=p^{-2}{p}^2=1$

• $z^{\prime }=x^{\prime }+i{y}^{\prime }$ allora $\exists \sigma$ tale che $x^{\prime }=\cos (\sigma )$ e $y^{\prime }=\sin (\sigma )$ (1)

  Sostituendo in $z^{\prime }$ otteniamo $z^{\prime }=\cos (\sigma )+i\sin (\sigma )=e^{i\sigma }$

  Quindi dato che $z^{\prime }=p^{-1}z$ possiamo dire che $z=p{e}^{i\sigma }$ (facendo la formula inversa)

Le soluzioni di (1) sono gli elementi $\sigma +2\pi \mathbb{Z}$ per un certo $\sigma \in [0,2\pi )$

• Su $\mathbb{R}$ c’è la relazione di congruenza $mod.2\pi$

$\alpha ,\beta \in \mathbb{R}$ diciamo che $\alpha {\equiv }_2\beta \iff \alpha -\beta \in 2\pi \mathbb{Z}$ da cui $\sigma +2\pi \mathbb{Z}$ è una classe di equivalenza e si identifica con un elemento di $\mathbb{R}/2\pi \mathbb{Z}$

Algebricamente Chiuso

Un $K$ campo è detto algebricamente chiuso se $\forall F\in K[X]\backslash K$ (tolte le costanti):

$$\exists x\in Kt.c.x\text{ eˋ radice di }F\iff \exists x\in K:X-x|F$$

Lemma

$K$ è algebricamente chiuso se i soli polinomi irriducibili e monici sono i polinomi $X-x,x\in K$, quindi di grado 1.

Dimostrazione

Parte $\Rightarrow$, sia $P\in K[X]$ irriducibile e monico. Siccome $K$ è chiuso algebricamente abbiamo che $\exists x\in K$ tale che $X-x|P$.

Quindi possiamo scrivere $P=(X-x)Q$ con $Q\in K[X]\backslash \{0\}$

Il grado di $P$ è quindi $deg(P)=1+deg(Q)$, se $deg(P)=1$ abbiamo dimostrato

Ma se $deg(P)\ge 2$ allora $deg(Q)\ge 1$ quindi $Q\notin K[X{]}^X=K^X$ ma anche $(X-x)\notin K[X{]}^X$ e questo contraddice $P$ irriducibile ($\Rightarrow deg(P)=1;\Rightarrow P=X-x$)

---

Parte $\Leftarrow$ Supponiamo $\{P\in K[X]\text{ monico e irriducibile}\}=\{X-x:x\in K\}$.

Sia $P$ monico con $deg\ge 1$ allora $P=\prod Q^{V_Q(P)}$

Da completare

---

Molteplicità

$K$ algebricamente chiuso $\Rightarrow \forall F\in K[X]\backslash \{0\}$ si scrive in modo unico come:

$$F=\underset{\in K^X}{\lambda }\prod _{x\in K}(X-x{)}^{V_X(F)}$$

Dove $V_X(F)$ è la molteplicità di $F$ in $x$

Si ha che $\{X:V_X(F)\ne 0\}=\{X:e{v}_X(F)=0\}=\{X\text{ radice di }F\}=\mathcal{R}$

Questo insieme ha cardinalità $\le deg(F):=n$

$$deg(F)=\sum _{x\in K}{V}_x(F)=\sum _{x\in \mathcal{R}}{V}_x(F)\ge \sum _{x\in \mathcal{R}}1=\text{cardinalitaˋ di }\mathcal{R}$$

Infatti un polinomio di grado $n$ ha $\le n$ soluzioni.

Teorema Fondamentale Algebra

$\mathbb{C}$ è algebricamente chiuso, omettiamo la dimostrazione.

Teorema

$\forall K$ campo esiste sempre un altro campo algebricamente chiuso che lo contiene ad esempio $\mathbb{R}$ non è algebricamente chiuso ma $\mathbb{R}\subset \mathbb{C}$.

---

Molte di queste cose le ho sistemate in un documento scritto dopo, lo caricherò da qualche parte su github =P.

---

Esempi Fattorizzazzione

Prendiamo un polinomio $X^n-1$ con $n\le 5$, questo polinomio ha sempre come radice $1$, inoltre se $n$ è pari come radice abbiamo anche $-1$. Quindi possiamo scriverlo:

$$X^n-1=(X-1)Q$$

Dove $Q$ è il quoziente della divisione euclidea con $X-1$ e ha quindi grado $n-1$, è unicamente determinato.

Possiamo scriverlo come:

$$Q=X^{n-1}+X^{n-2}+\cdots +X+1$$

Ovvero tutte le potenze di $X$ con coefficiente 1, ha in totale $n$ termini. Perché possiamo scriverlo così? Facciamo la moltiplicazione:

$$(X-1)(X^{n-1}+\cdots +X+1)=X^n+X^{n-1}+\cdots +X+1-(X^{n-1}+\cdots +X+1)=X^n-1$$

Infatti escluso primo e ultimo termine gli altri si cancellano tutti fra loro.

Esempio con n=3

$$X^3-1=(X-1)(X^2+X+1)$$

Dato che $\Delta (X^2+X+1)<0$, questa è la sua fattorizzazzione in $\mathbb{R}[X]$, ma possiamo continuare in $\mathbb{C}[X]$, infatti qui gli irriducibili sono solo i polinomi nella forma $X-x$ con $x\in \mathbb{C}$.

Calcoliamo le radici di quel polinomio di grado 2 in $\mathbb{C}[X]$ e manteniamo $X-1$ di $\mathbb{R}[X]$:

$$X^2+X+1=\left(X+\frac{1}{2}+i\frac{\sqrt{3}}{2}\right)\left(x+\frac{1}{2}+i\frac{\sqrt{3}}{2}\right)$$

Tutte le sue radici si trovano nel cerchio unità, rappresentiamole:

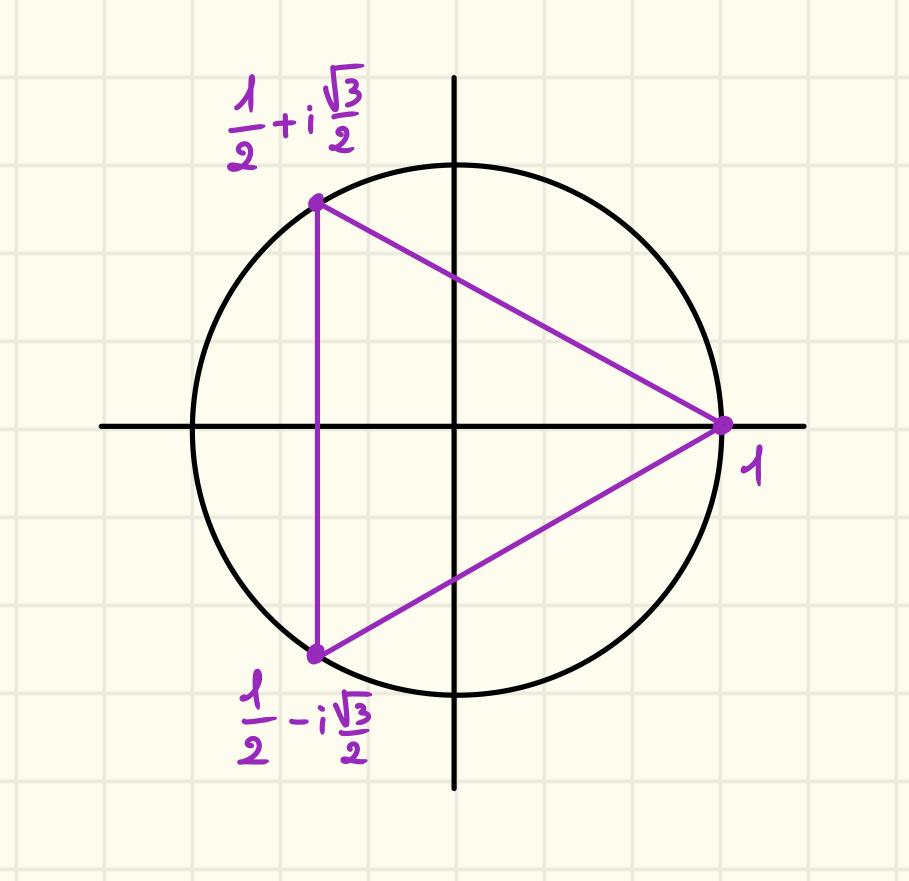
Possiamo anche scriverle in forma esponenziale, $X^3-1$ ha come radici:

• $X^0=1$
• $X^1$
• $X^2$

Dato $X=e^{\frac{i2\pi }{3}}=\cos \left(\frac{2\pi }{3}\right)+i\sin \left(\frac{2\pi }{3}\right)$.

Esempio n=4

Come detto prima oltre alla radice $1$ abbiamo anche radice $-1$, quindi:

$$X^4-1=(X-1)(X+1)(X^2+1)$$

Questa è la sua fattorizzazzione in $\mathbb{R}[X]$, mentre in $\mathbb{C}[X]$ abbiamo:

$$(X-1)(X+1)(X-i)(X+i)$$

Che scritta in forma esponenziale:

$$(X-x^0)(X-x^1)(X-x^2)(X-x^3)x=e^{\frac{i2\pi }{4}}=\cos \left(\frac{\pi }{2}\right)+i\sin \left(\frac{\pi }{2}\right)$$

Anche queste sono tutte sul cerchio unità, rappresentiamole:

Cosa iniziamo a notare?

Che se ci sono radici complesse, allora ci sono anche le loro coniugate, questo è sempre vero per polinomi in $\mathbb{R}[X]$, queste coppie ci danno dei fattori irriducibili in $\mathbb{R}[X]$.

Esempio n=5

$$X^5-1=(X-1)\underset{\text{Riducibile in }\mathbb{R}[X]}{\underbrace{(X^4+X^3+X^2+X+1)}}$$

Il polinomio di grado 4 che vediamo ha un fattore di grado 1 se e solo se ha una radice reale e questo se e solo se $X^5-1$ ha una radice reale differente da 1.

Vediamo le radici in $\mathbb{C}[X]$:

$$\begin{array}{rl}& (e^{\frac{i2\pi }{5}}{)}^k\text{ con }k=0,1,2,3,4\text{ sostituamolo:}\\ & \\ & ((e^{\frac{i2\pi }{5}}{)}^k{)}^5=(e^{i2\pi }{)}^k=1\text{ sono tutte radici distinte}\end{array}$$

Sono distinte perché:

$${\left(e^{\frac{2\pi i}{5}}\right)}^k=\cos \left(\frac{2\pi k}{5}\right)+i\sin \left(\frac{2\pi k}{5}\right)$$

Che graficamente:

Con $x=e^{\frac{2\pi i}{5}}$.

Notiamo che abbiamo una sola radice reale quindi $X^4+X^3+X^2+X+1$ si spezza in due polinomi di grado 2.

Scriviamo questi polinomi:

$$\begin{array}{r}{P}_1=(X-x)(X-x^4)\in \mathbb{R}[X]\\ P_2=(X-x^2)(X-x^3)\in \mathbb{R}[X]\end{array}$$

Infatti:

$$P_1=(X-x)(X-\overline{x})=X^2-X\underset{\in \mathbb{R}}{\underbrace{(x+\overline{x})}}+\underset{1}{\underbrace{\stackrel{|x{|}^2}{\overbrace{x\overline{x}}}}}$$ $$P_2=(X-x^2)(X-\overline{x^2})=X^2-X\underset{\in \mathbb{R}}{\underbrace{(x^2+\overline{x^2})}}+\underset{1}{\underbrace{\stackrel{|x^2{|}^2}{\overbrace{x^2\overline{x^2}}}}}$$

Infatti se scriviamo $x=\alpha +i\beta$ e $\overline{x}=\alpha -i\beta$ notiamo che:

$$x+\overline{x}=2\alpha \text{ e quindi eˋ reale}$$

Mentre

$$x\cdot \overline{x}={\alpha }^2+{\beta }^2=1\text{ dato che sta sul cerchio unitaˋ}$$

Effettuiamo i calcoli:

$$\begin{array}{rl}& x+\overline{x}=2\mathrm{Re}(x)=2\cos \left(\frac{2\pi }{5}\right)\\ & x^2+\overline{x^2}=2\mathrm{Re}(x^2)=2\cos \left(\frac{4\pi }{5}\right)\\ & \\ & P_1=x^2-2\cos \left(\frac{2\pi }{5}\right)X+1\\ & P_2=x^2-2\cos \left(\frac{4\pi }{5}\right)X+1\end{array}$$

Quindi possiamo scrivere:

$$X^5-1=\underset{\text{Fattorizzazzione }\mathbb{C}[X]}{\underbrace{\prod _{i=0}^4(X-x^i)}}=(X-x^0)(X-x)(X-\overline{x})(X-x^2)(X-\overline{x^2})=(X-x^0)P_1\cdot P_2$$

Dove i due polinomi:

$$P_1\cdot P_2=X^4+X^3+X^2+X+1$$

Caso veloce n=7

Avremo la stessa situazione, quindi:

$$X^7-1=(X-x^0)\stackrel{P_1}{\overbrace{\left(X^2-2\cos \left(\frac{2\pi }{7}\right)+1\right)}}\stackrel{P_2}{\overbrace{\left(X^2-2\cos \left(\frac{4\pi }{7}\right)+1\right)}}\stackrel{P_3}{\overbrace{\left(X^2-2\cos \left(\frac{6\pi }{7}\right)+1\right)}}$$

---

Quindi l’esponenziale di Eulero ci permette di fattorizzzare polinomi $X^n-1$ con $n>1$ nella forma:

$$X^n-1=\prod _{i=0}^{n-1}(X-x^i)\text{ con }x=e^{\frac{i2\pi }{n}}$$

E la radici si trovano in un poligono inscritto nel cerchio unità, ovvero sono i suoi vertici. Sappiamo che una si trova in $-1$ se $n$ è pari. Questa è la fattorizzazzione in $\mathbb{C}[X]$.

Coniugato di un Polinomio

Dato $F=f_0+f_{1}X+\cdots +f_n{X}^n\in \mathbb{C}[X]$ e ogni $f_{\cdot }\in \mathbb{C}$ poniamo:

$$\overline{F}=\overline{f_0}+\overline{f_1}X+\cdots +\overline{f_n{X}^n}$$

Osserviamo che:

$$F\in \mathbb{R}[X]\iff F=\overline{F}\text{ inoltre se }F\in \mathbb{R}[X]ee{v}_z(F)=0\text{ allora }e{v}_{\overline{z}}(F)=0$$

Dimostrazione

$$e{v}_{\overline{z}}(F)=e{v}_{\overline{z}}(\overline{F})\underset{\text{Per comp. di }\overline{\cdot }}{=}\overline{e{v}_z(F)}=\overline{0}=0$$

Le radici di un polinomio in $\mathbb{R}[X]$ sono sempre o reali o 2 a 2 complessi coniugati. Questo implica un lemma.

Lemma

Dato $F\in \mathbb{R}[X]$ e detto $\mathcal{R}$ l’insieme delle sue radici, allora:

$$\mathcal{R}={\mathcal{R}}_{\mathbb{R}}\bigsqcup {\mathcal{R}}_{\mathbb{C}\backslash \mathbb{R}}^{+}\bigsqcup {\mathcal{R}}_{\mathbb{C}\backslash \mathbb{R}}^{-}$$

Dove:

• ${\mathcal{R}}_{\mathbb{R}}$ indica le radici reali
• ${\mathcal{R}}_{\mathbb{C}\backslash \mathbb{R}}^{+}$ indica le radici immaginarie con parte immaginaria positiva
• ${\mathcal{R}}_{\mathbb{C}\backslash \mathbb{R}}^{-}$ indica radici immaginarie con parte immaginaria negativa

Graficamente

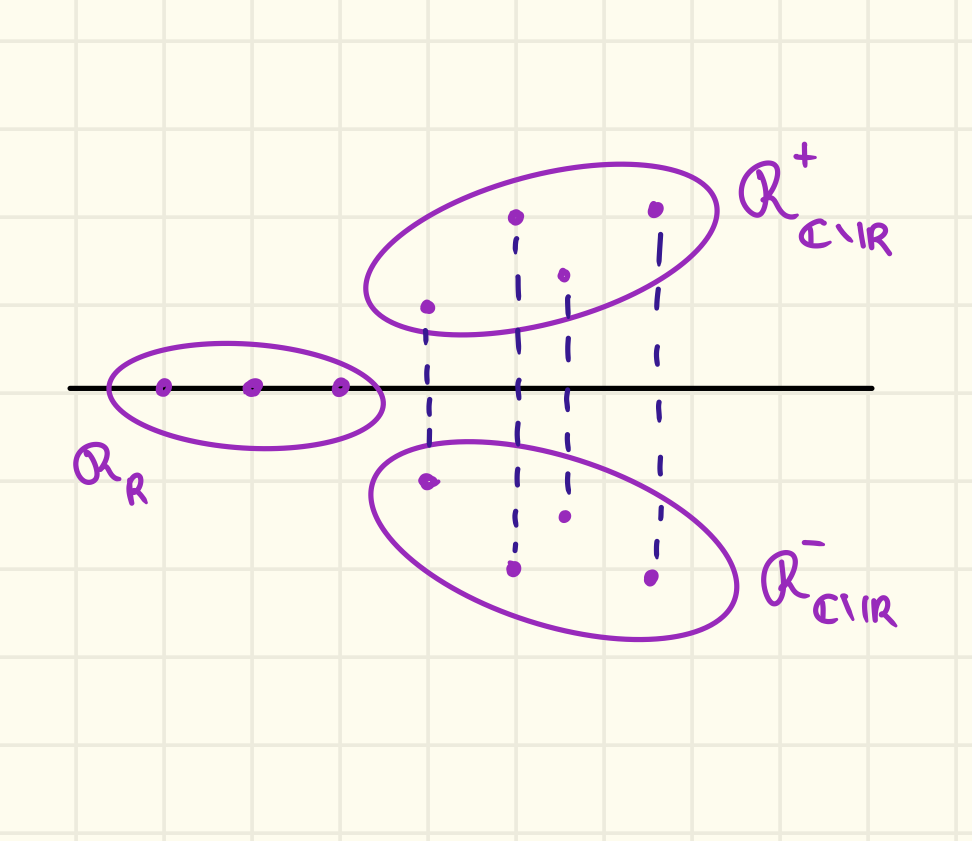
Possiamo dire che:

$${\mathcal{R}}_{\mathbb{C}\backslash \mathbb{R}}={\mathcal{R}}_{\mathbb{C}\backslash \mathbb{R}}^{+}\bigsqcup {\mathcal{R}}_{\mathbb{C}\backslash \mathbb{R}}^{-}$$

E inoltre i complessi sono coniugati quindi:

$$\overline{{\mathcal{R}}_{\mathbb{C}\backslash \mathbb{R}}^{-}}={\mathcal{R}}_{\mathbb{C}\backslash \mathbb{R}}^{+}$$

Lemma

$X^2+\beta X+\gamma \in \mathbb{R}[X]$ è irriducibile in $\mathbb{R}[X]\iff \Delta ={\beta }^2-4\gamma <0$

Dimostrazione

Supponiamo $P$ irriducibile e quindi non ha radici reali ${\mathcal{R}}_{\mathbb{R}}=\varnothing$

Ha però due radici complesse $z$ e $\overline{z}$ dato che $deg(P)=2$. Scriviamo quindi:

$$P=(X-z)(X-\overline{z})=X^2-\underset{2\mathrm{Re}(z)}{\underbrace{(z+\overline{z})}}X+\underset{|z{|}^2}{\underbrace{z\overline{z}}}$$

Adesso calcoliamo $\Delta$:

$$\begin{array}{rl}(z+\overline{z}{)}^2-4z\overline{z}& =z^2+2z\overline{z}+{\overline{z}}^2-4z\overline{z}\\ & =z^2-2z\overline{z}+{\overline{z}}^2=(z-\overline{z}{)}^2\\ & \\ & \text{Scriviamo }z=x+iyx,y\in \mathbb{R}\\ & \\ & z-\overline{z}=2iy\text{ quindi }(2iy{)}^2=-4y^2\text{ che eˋ }<0\end{array}$$

Lemma

Ogni $F\in \mathbb{R}[X]$, in $\mathbb{R}[X]$ si spezza come:

$$F=\underset{\in {\mathbb{R}}^X}{\lambda }\prod _{x\in {\mathcal{R}}_{\mathbb{R}}}(X-x)\underset{\text{Polinomio di grado 2 irr. in }\mathbb{R}[X]}{\underbrace{\prod _{z\in {{\mathcal{R}}^{+}}_{\mathbb{C}\backslash \mathbb{R}}}[(X-z)(x-\overline{z})]}}$$

Esercizio / Proprietà

Sia $P\in \mathbb{R}[X]$ di grado dispari allora $P$ ammette almeno una radice reale. Infatti il lemma ci dice che:

$$deg(P)=\#{\mathcal{R}}_{\mathbb{R}}+\#{\mathcal{R}}_{\mathbb{C}\backslash \mathbb{R}}=\underset{\text{Mostrare che }\ne 0}{\underbrace{\stackrel{r}{\overbrace{\#{\mathcal{R}}_{\mathbb{R}}}}}}+2\stackrel{s}{\overbrace{\#{\mathcal{R}}_{\mathbb{C}\backslash \mathbb{R}}^{+}}}$$

Ovvero vogliamo mostrare che c’è almeno una radice reale.

Siccome $deg(P)$ è dispari allora $deg(P)=2n+1$ scriviamo:

$$2n+1=2s+r\to r=2(n-s)+1\Rightarrow r{\equiv }_{2}1\Rightarrow r\ne 0$$

Un’altra strada che possiamo prendere è quella di utilizzare il Teorema dei Valori Intermedi, ovvero l’analisi matematica. Infatti è impossibile dimostrare che $\mathbb{C}$ è algebricamente chiuso basandosi solo sull’algebra, ci serve anche l’analisi matematica, nello specifico il Teorema dei valori intermedi.

Possibili fattorizzazioni in $\mathbb{Q}$

Prendiamo $Q\in \mathbb{Q}[X]$ o qualsiasi campo, scriviamo per ogni grado tutti i casi possibili:

• Se $deg(Q)=1$

  • Irriducibile

• Se $deg(Q)=2$

  • Irriducibile
  • $P_1{P}_2$ entrambi di grado 1 e irriducibili

• Se $deg(Q)=3$

  • Irriducibile
  • $P_1{P}_2$ con $P_1$ grado 1 e $P_2$ grado 2 irriducibili
  • $P_1{P}_2{P}_3$ tutti irriducibili di grado 1

In tutti questi casi se $Q$ non è irriducibile su $K$ allora ammette sempre almeno una radice, nel caso di grado uguale a 4 questo non è vero

• Se $deg(Q)=4$
  • Irriducibile
  • $P_1{P}_2$ con uno grado 1 e uno grado 3
  • $P_1{P}_2$ entrambi grado 2, ma non abbiamo radici
  • $P_1{P}_2{P}_3$ due di grado 1 e uno di grado 3
  • $P_1{P}_2{P}_3{P}_4$ tutti di grado 1

Ecc…

Teoria dei Gruppi

Dato un insieme $G\ne \varnothing$ con $\ast$ operazione binaria su $G$ e quindi definita come:

$$G\times G\to G|(a,b)\to a\ast b$$

Inoltre selezioniamo un elemento $e\in G$ allora la terna $G=(G,+,e)$ è un gruppo se:

1. $\forall a,b,c\in G$ abbiamo che $a\ast (b\ast c)=(a\ast b)\ast c$ e scriviamo quindi $a\ast b\ast c$ | Associatività
2. $\forall a\in G$ si verifica $a\ast e=e\ast g=a$ | Elemento neutro per l’operazione binaria
3. $\forall a\in G$ deve $\exists a^{\prime }\in G$ tale che $a\ast a^{\prime }=a^{\prime }\ast a=e$ | Inverso per l’operazione

Inoltre se si verifica anche: 4) $\forall a,b\in G,a\ast b=b\ast a$ allora $G$ è un gruppo abeliano (o commutativo)

Gruppi in Notazione Additiva

La terna $(G,+,0)$ dove scriviamo $+$ per l’operazione e $0$ o $0_G$ per l’elemento neutro si dive in notazione additiva, di solito i gruppi in questa notazione sono anche commutativi e in questa notazione l’inverso di $a\in G$ si chiama opposto e si scrive $-a$.

Ad esempio dato un anello $(A,+,-,\cdot ,1_A,0_A)$ se lo scriviamo $(A,+,0_A)$ è un gruppo in notazione additiva, inoltre è un gruppo abeliano dato che è derivato da un anello (sicuramente additivo per definizione). Inoltre possiamo prendere come esempio anche $\mathbb{Z}=(\mathbb{Z},+,0)$, $\mathbb{R}=(\mathbb{R},+,0)$ o anche $K=(K,+,0)$ con $K$ un qualsiasi campo.

Gruppi in notazione Moltiplicativa

La terna $(G,\cdot ,1)$ dove scriviamo $\cdot$ per l’operazione e $1$ o $1_G$ per l’elemento neutro si dicono in notazione moltiplicativa.

Ad esempio se prendiamo $(A,+,-,\cdot ,1_A,0_A)$ Anello, allora $A^X=(A^X,\cdot ,1)$ è un gruppo in notazione moltiplicativa, infatti abbiamo visto che il prodotto di elementi invertibili è invertibile, il prodotto è associativo e infine se $a,b\in A^X$ allora $ab\in A^X$ e inoltre sappiamo che $(ab{)}^{-1}=b^{-1}{a}^{-1}$. $A^X$ è abeliano.

Sottogruppo

Dato un gruppo $G$ in notazione moltiplicativa e un sottoinsieme $H\subset G$ non vuoto, si dice che $H$ è un sottogruppo di $G$ se $\forall a,b\in H$ si ha che $a\cdot b^{-1}\in H$. Si scrive $H<G$.

Osservazione

$H$ è un gruppo. Se $a\in H$ allora $a{a}^{-1}=1_G\in H$. Ma allora $\forall b\in H,1_G\cdot b^{-1}=b^{-1}\in H$ inoltre $1_G=1_H$ e $\forall b\in H,b^{-1}\in H$.

Infine se $a,b\in H$ e anche $b^{-1}\in H$ allora $a(b^{-1}{)}^{-1}\in H$

Esempio $\mathbb{Z}<\mathbb{Q}<\mathbb{R}<\mathbb{C}$

In notazione additiva per il sottogruppo deve verificarsi:

$$H<G\iff \forall a,b\in H,a-b\in H$$

Omomorfismi di gruppi

Dati $G_1,G_2$ due gruppi in notazione moltiplicativa e sia $G_1\stackrel{f}{\to }{G}_2$ un’applicazione, $f$ si dice omomorfismo di gruppi se:

1. $f(1_{G_1})=1_{G_2}$
2. $\forall a\in G_1,\underset{\text{Inverso in }{G}_1}{\underbrace{f(a^{-1})}}=\underset{\text{Inverso in }{G}_2}{\underbrace{f(a{)}^{-1}}}$
3. $\forall a,b\in G_1,f(\underset{\text{operazione }{G}_1}{\underbrace{ab}})=f(a)(\text{operazione }{G}_2)f(b)$ Esercizio

Mostrare che $f:G_1\to G_2$ è un omomorfismo di gruppi $\iff a,b\in G,f(a{b}^{-1})=f(a)f(b{)}^{-1}$

Isomorfismo

Sia $f:G_1\to G_2$ un omomorfismo di gruppi, se $f$ è biiettiva allora si dice che $f$ è isomorfismo

Esercizio

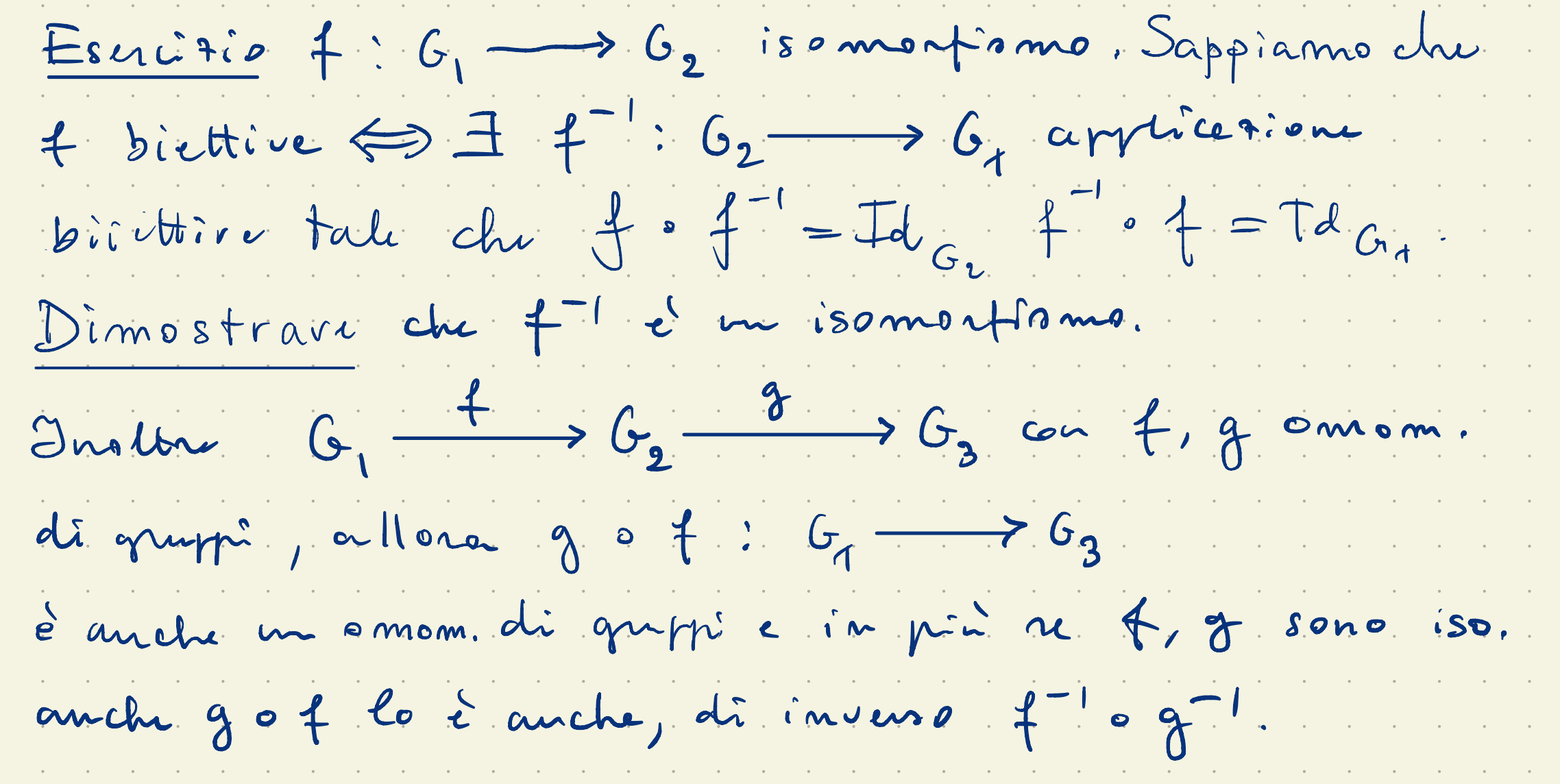
Quindi se $f$ è isomorfismo lo è anche $f^{-1}$, inoltre date due funzioni $f,g$ omomorfismi allora anche $g\circ f$ è omomorfismo. In più se sono isomorfismi allora lo è anche $g\circ f$, anche di inverso $f^{-1}\circ g^{-1}$.

Esempi

Prendiamo tutto in notazione additiva

$$\mathbb{Z}\stackrel{f}{\to }m\mathbb{Z}<\mathbb{Z}$$

Osserviamo che $m\mathbb{Z}$ è un gruppo e un sottogruppo di $\mathbb{Z}$.

Definiamo $f(n):=mn$ con $m\ne 0$ applicazione, questa è isomorfismo di gruppi infatti:

1. $f(n-n^{\prime })=m(n-n^{\prime })=mn-m{n}^{\prime }=f(n)-f(n^{\prime })\Rightarrow$ è omomorfismo
2. $f$ iniettiva: $f(p)=f(q)\iff pm=qn\iff m(p-q)=0\iff p=q$
3. $f$ suriettiva: Sia $y\in m\mathbb{Z}$ allora $\exists k\in \mathbb{Z}$ t.c. $y=mk$, ponendo $x=k$ si ha $f(x)=mk=y$

---

Altro esempio, mischiando $+,\cdot$

$G_1=\mathbb{R}$ con operazione $+$.

$G_2={\mathbb{R}}_{>0}$ ovvero i reali positivi con operazione $\cdot$, da notare che ${\mathbb{R}}_{>0}<{\mathbb{R}}^X$, adesso poniamo:

$$\begin{array}{rl}& f:\mathbb{R}\to {\mathbb{R}}_{>0}f(x):=e^x\\ & g:{\mathbb{R}}_{>0}\to \mathbb{R}g(y):=\log (y)\end{array}$$

Sono due isomorfismi di gruppi, l’uno inverso dell’altro. Quindi abbiamo che $f^{-1}=g$ e $g^{-1}=f$, inoltre:

$$\begin{array}{rl}& f(0)=e^0=1=1_{G_2}\in G_2\\ & f(-x)=e^{-x}=(e^x{)}^{-1}\text{ Compatibile con inverso}\\ & f(x-x^{\prime })=e^{x-x^{\prime }}=e^x{e}^{-x^{\prime }}=f(x)f(x^{\prime }{)}^{-1}\end{array}$$

In modo analogo:

$$\begin{array}{rl}& g(1)=0\\ & g(y^{-1})=\log (y^{-1})=-g(y)\\ & g(y^{\prime }{y}^{-1})=g(y^{\prime })-g(y)\text{ infatti sarebbe }\log \left(\frac{y^{\prime }}{y}\right)=\log (y^{\prime })-\log (y)\end{array}$$

Costruzioni canoniche di un sottogruppo

Sia $G_1\stackrel{f}{\to }{G}_2$ omomorfismo in notazione moltiplicativa.

Lemma

Sia $f:G_1\to G_2$ un omomorfismo di gruppi indichiamo con:

$$H=\{g\in G_1:f(g)=1_{G_2}\}=f^{-1}(\{1_{G_2}\})\subset G_1$$

Ovvero gli elementi di $G_1$ che puntano all’elemento neutro di $G_2$, questo è un sotto gruppo di $G_1$: $H<G_1$ e si chiama nucleo di $f$, lo indichiamo con $H=Ker(f)$ (kernel).

Osservazione

Un gruppo qualsiasi ha due sottogruppi evidenti: $\{1_G\}$ e se stesso, se in notazione additiva allora $\{0_G\}$

Dimostrazione

Dati $a,b\in H$ con $f(a)=f(b)=1_{G_2}$.

$$f(a{b}^{-1})=f(a)f(b^{-1})=f(a)f(b{)}^{-1}=1G_{2}1G_2^{-1}=1G_2$$

Quindi $a{b}^{-1}\in H$ dato che in $H$ abbiamo tutti gli elementi che puntano a $1G_2$

Lemma

Sia $f:G_1\to G_2$ un omomorfismo di gruppi si ha che:

$$Ker(f)=\{1_{G_1}\}\iff f\text{ eˋ iniettiva}$$

Questo è detto kernel banale dato che per definizione di omomorfismo di gruppi $f(1_{G_1})=1_{G_2}$

Questo è il più piccolo sottogruppo di $G_1$.

Dimostrazione

Dimostriamo la parte $\Rightarrow$

Quindi supponiamo che $Ker(f)=1_G=\{x\in G_1:f(x)=1_{G_2}\}$

Siano $x,x^{\prime }\in G_1$ tali che $f(x)=f(x^{\prime })\underset{\text{Divisione}}{\underbrace{\iff }}f(x)f(x^{\prime }{)}^{-1}=1_{G_2}$

Per omomorfismo possiamo dire che $f(x)f(x^{\prime }{)}^{-1}=f(x{x}^{\prime -1})$

Quindi $x(x^{\prime }{)}^{-1}\in Ker(f)=\{1_{G_1}\}$ dato che la sua $f$ punta a $G_2$, questo significa che $x(x^{\prime }{)}^{-1}=1G_1$, possiamo poi moltiplicare per $x^{\prime }$ e ottenere:

$$x(x^{\prime }{)}^{-1}\cdot x^{\prime }=1_{G_1}\cdot x^{\prime }\iff x^{\prime }=x$$

Quindi $f$ è iniettiva.

Dimostriamo la parte $\Leftarrow$

Supponiamo quindi $f$ iniettiva e sia $x\in Ker(f)$ e allora $f(x)=1_{G_2}$.

Ma $f$ è un omomorfismo di gruppi da cui deduciamo che $f(1_{G_1})=1_{G_2}$.

Siccome $f(x)=f(1_{G_1})=1_{G_2}$ e $f$ iniettiva, dobbiamo avere che $x=1_{G_1}\Rightarrow Ker(f)=\{1_{G_1}\}$

Esercizio Gruppi - Sottogruppo Immagine

Data una funzione $f:G_1\to G_2$ e omomorfismo di gruppi con $f(G_1)\subset G_2$, infatti:

$$f(G_1)=\{y\in G_2:\exists x\in G_1\text{ con }f(x)=y\}$$

Dimostrare che $f(G_1)<G_2$, sottogruppo immagine, ovvero dimostrare che se $y,y^{\prime }\in f(G_1)$ allora $y(y^{\prime }{)}^{-1}\in f(G_1)$.

Soluzione

$$\begin{array}{rl}& \exists x,x^{\prime }\in G_{1}t.c.f(x)=yf(x^{\prime })=y^{\prime }\\ & \\ & y(y^{\prime }{)}^{-1}=f(x)f(x^{\prime }{)}^{-1}=f(\underset{\text{Elemento di }{G}_1}{\underbrace{x(x^{\prime }{)}^{-1}}})=f(z)\text{ con }z\in G_1\\ & \\ & \text{Abbiamo mostrato che:}\\ & \\ & \exists z\in G_{1}t.c.f(z)=y(y^{\prime }{)}^{-1}\iff y(y^{\prime }{)}^{-1}\in f(G_1)\end{array}$$

Sottogruppi Coniugati

Dato un gruppo $G$, un altro gruppo $H<G$ e un elemento $g\in G$, definiamo:

$$H^g:=\underset{\text{Coniugato di H per g}}{\underbrace{\{g^{\prime }\in Gt.c.\exists h\in Ht.c.g^{\prime }=g^{-1}hg\}}}$$

Osservazione

Se $G$ è abeliano allora $g^{-1}hg=h$ e quindi $H^g=H\forall g$, per gruppi abeliani quindi non ci porta a nulla questo insieme.

Nota

Ricordiamo che se un gruppo non è abeliano allora $(abc{)}^{-1}=c^{-1}{b}^{-1}{a}^{-1}$, mentre se è abeliano e quindi commutativo non ci importa dell’ordine.

Lemma $H^g<G$

Dimostrazione

Prendiamo due elementi $a,b\in H^g$, vogliamo dimostrare che $a{b}^{-1}\in H^g$, per definizione possiamo scrivere (con $g$ fissato):

$$\begin{array}{rl}& a=g^{-1}{a}^{\prime }g\exists a^{\prime }\in H\\ & b=g^{-1}{b}^{\prime }g\exists b^{\prime }\in H\\ & \\ & a{b}^{-1}=g^{-1}{a}^{\prime }g{g}^{-1}(b^{\prime }{)}^{-1}g=g^{-1}\underset{\in H\text{ visto che }H<G}{\underbrace{a^{\prime }(b^{\prime }{)}^{-1}}}g\Rightarrow a{b}^{-1}\in H^g\forall a,b\in H^g\Rightarrow H^g<G\end{array}$$

Dimostrazione Alternativa

Definiamo dato $g\in G$, un’applicazione $G\stackrel{fg}{\to }G$, $x\to fg(x)=g^{-1}xg$ e osserviamo che $\forall g$, $fg$ è un omomorfismo di gruppi (e dato che va $G$ a $G$, si parla di endomorfismo), per verificarlo devo mostrare che $\forall a,b\in G,f(a{b}^{-1})=f(a)fg(b^{-1})$

$$fg(a)fg(b^{-1})=g^{-1}ag(g^{-1}bg{)}^{-1}=g^{-1}ag{g}^{-1}{b}^{-1}(g^{-1}{)}^{-1}=g^{-1}a{b}^{-1}g=fg(a{b}^{-1})$$

Questo dimostra perché se $H<G_1$ e $G_1\stackrel{f}{\to }{G}_2$ omomorfismo allora $f(G_1)<G_2$, se $G_1=G_2=G$ e $f=fg$ otteniamo che $\forall H<G,\underset{g^{-1}Hg=H^g}{\underbrace{fg(H)}}<G\Rightarrow H^g<G$

Permutazioni

Dato $\mathcal{E}$ insieme finito, sia $S(\mathcal{E})=\{f:\mathcal{E}\to \mathcal{E}:f\text{ biiettiva}\}$ gli elementi di questo insieme sono chiamati permutazioni.

Su $S(\mathcal{E})$ esiste l’operazione di composizione di applicazioni:

$$\mathcal{E}\stackrel{f}{\to }\mathcal{E}\stackrel{g}{\to }\mathcal{E}allora\mathcal{E}\stackrel{g\circ f}{\to }\mathcal{E}$$

E se $f,g\in S(\mathcal{E})$ allora $g\circ f\in S(\mathcal{E})$.

Inoltre $(g\circ f{)}^{-1}=f^{-1}\circ g^{-1}\Rightarrow (S(\mathcal{E}),\circ ,I{d}_{\mathcal{E}})\text{ eˋ un gruppo}$ perché:

• $f\circ (g\circ h)=(f\circ g)\circ h$, associativo
• $f\circ Id=Id\circ f=f\forall f\in S(\mathcal{E})$, elemento neutro
• $\forall f\in S(\mathcal{E})$ invertibile e $f\circ f^{-1}=f^{-1}\circ f\in S(\mathcal{E})$ inverso per $\circ$

Sia $\mathcal{E}=\{1,\dots ,n\}=:I_n$ con $n\ge 1$ allora si scrive $S_n=S(I_n)(=S(\mathcal{E}))$

Ogni elemento di $S_n,f\in S_n$ può essere identificato con un diagramma:

Definizione di n-ciclo

È una permutazione del tipo:

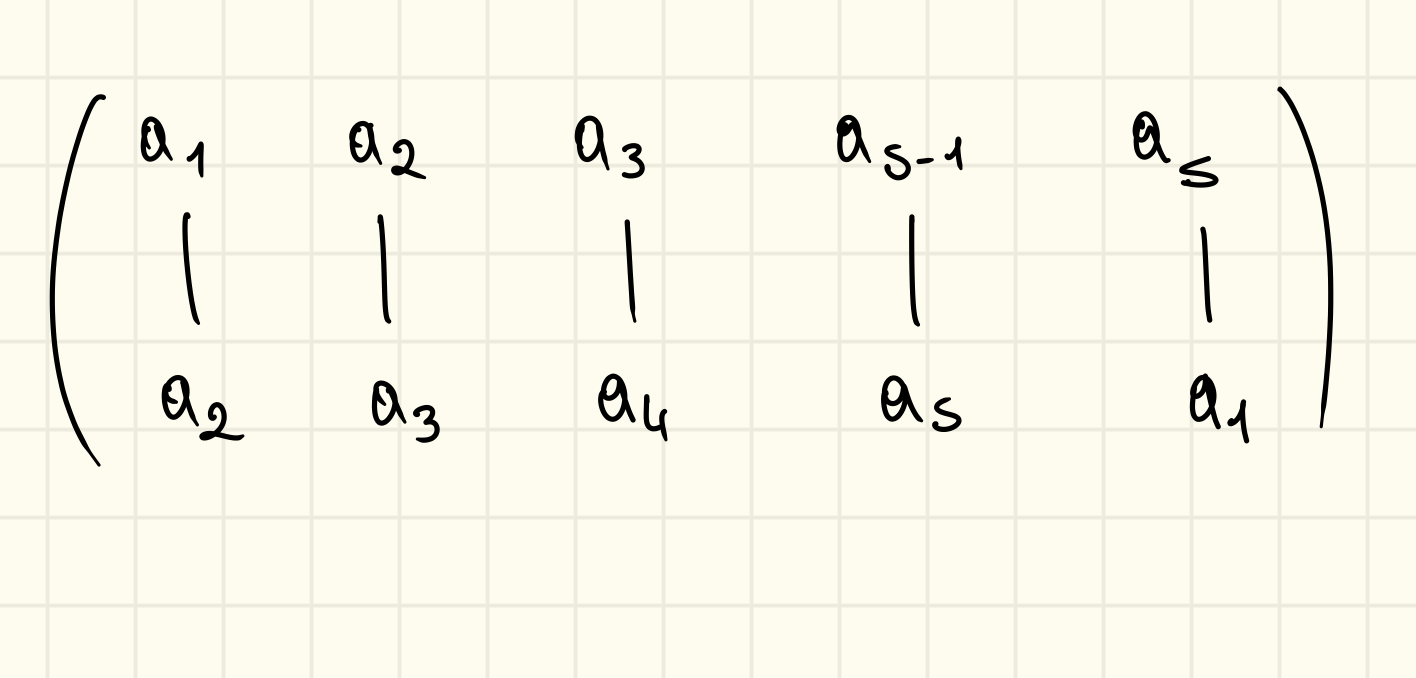
Con $a_1,a_2,\dots a_s\in I_n$ con $s\le n$ distinti, che fissa ovvero manda su se stessi tutti gli elementi che non appartengono a $\{a_1,\dots ,a_s\}$, invece quelli che ci appartengono li manda in maniera ciclica su di loro quindi $a_1\to a_2\to a_3\to a_s\to a_1$, si chiama s-ciclo e si scrive $(a_1{a}_2\dots a_s)$ e bisogna rispettare l’ordine del ciclo nella notazione.

Esempi

Terminologia

Tutti i 2-cicli si chiamano trasposizioni, l’identità è uno 0-ciclo

Nota

Tutti i cicli sono permutazioni, ma non tutte le permutazioni sono cicli:

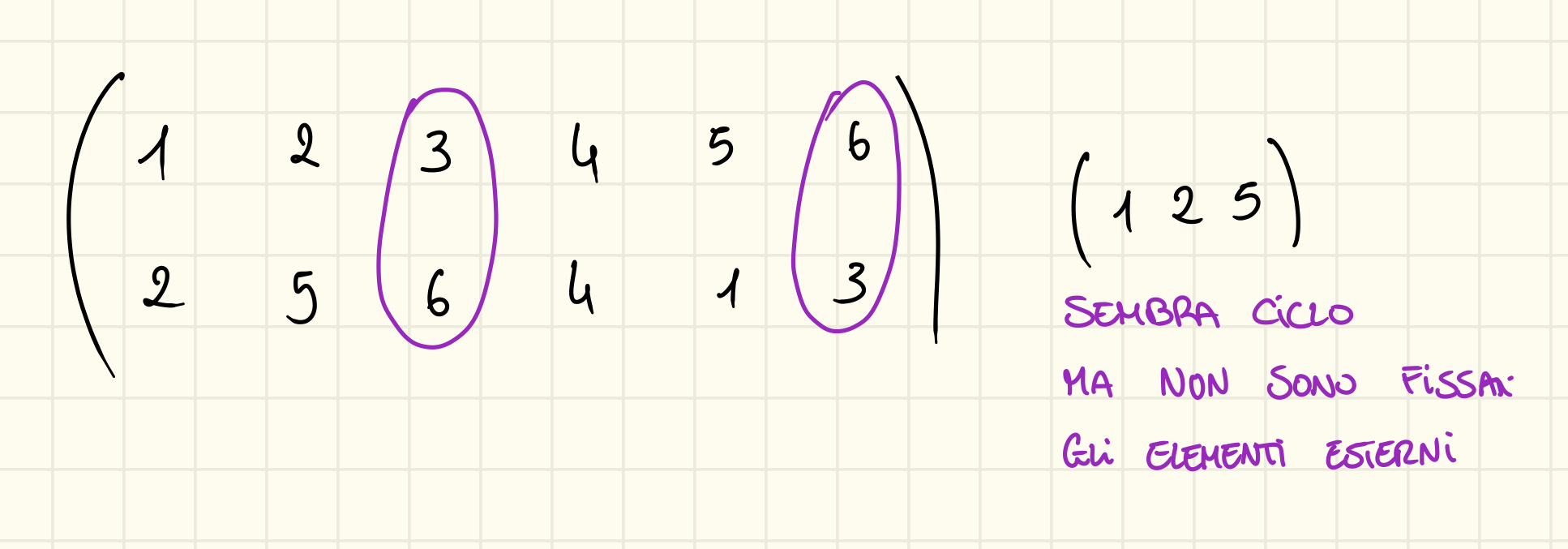
Inversione

$${\left(\begin{array}{ccccccc}1& 2& 3& 4& 5& 6& 7\\ 4& 6& 7& 5& 1& 3& 2\end{array}\right)}^{-1}=\left(\begin{array}{ccccccc}4& 6& 7& 5& 1& 3& 2\\ 1& 2& 3& 4& 5& 6& 7\end{array}\right)$$

Ovviamente possiamo anche cambiare l’ordine delle colonne, l’importante è mantenere le associazioni.

Nella notazione a ciclo l’inverso si ottiene leggendo da destra a sinista:

$$(a_1{a}_2\dots a_s{)}^{-1}=(a_s\dots a_2{a}_1)$$

Composizione (o Prodotto)

Definiamo

$$\sigma =\left(\begin{array}{ccccc}1& 2& 3& 4& 5\\ 3& 1& 4& 2& 5\end{array}\right)=(1342)\in S_5,\tau =\left(\begin{array}{ccccc}1& 2& 3& 4& 5\\ 5& 4& 2& 1& 3\end{array}\right)=(15324)\in S_5$$

Calcoliamo $\sigma \circ \tau =\sigma \tau$, agisce prima $\tau$

Quindi il risultato sarà:

$$\left(\begin{array}{ccccc}1& 2& 3& 4& 5\\ 5& 2& 1& 3& 4\end{array}\right)=(543)$$

Se calcoliamo invece $\tau \sigma$ e quindi agisce prima $\sigma$:

$$\left(\begin{array}{ccccc}1& 2& 3& 4& 5\\ 2& 5& 1& 4& 3\end{array}\right)=(1253)$$

I due cicli non sono uguali dato che $S_5$ non è commutativo.

Descrizione di $S_3$

Quindi abbiamo che:

$$S_3=\{Id,(23),(12),(123),(132),(13)\}$$

Ogni permutazione è un s-ciclo con $s=0,2,3$.

Quindi $\#S_3=3\cdot 2\cdot 1$

• Qual è il più piccolo $n$ t.c. in $S_n$ esiste una permutazione che non è un ciclo? $n=4$

Infatti prendiamo ad il prodotto $(12)(34)$ e calcoliamo i valori per $1,2,3,4$:

$$\begin{array}{r}(12)(34)(1)=(12)((34)(1))=(12)(1)=2\\ (12)(34)(2)=(12)((34)(2))=(12)(2)=1\\ (12)(34)(3)=(12)((34)(3))=(12)(4)=4\\ (12)(34)(4)=(12)((34)(4))=(12)(3)=3\end{array}$$

$(12)(34)(1)$ significa che applichiamo all’elemento 1 il ciclo $(34)$ che lascia invariato 1 e poi ci applichiamo il ciclo (12) che lo porta in 2.

In questo modo otteniamo:

$$\left(\begin{array}{cccc}1& 2& 3& 4\\ 2& 1& 4& 3\end{array}\right)$$

Che non è un ciclo

Esercizio

Mostrare che $(123{)}^{-1}=(132)$:

$$(123)=\left(\begin{array}{ccc}1& 2& 3\\ 2& 3& 1\end{array}\right);(123{)}^{-1}=\left(\begin{array}{ccc}1& 2& 3\\ 3& 1& 2\end{array}\right)=(132)$$

Cicli a Supporti Disgiunti

Dati due cicli $(a_1\dots a_s)$ e $(b_1\dots b_s)$ di $S_n$, si dice che sono a supporti disgiunti se $\{a_1,\dots ,a_s\}\cap \{b_1,\dots ,b_s\}=\varnothing$.

Più generalmente dati $r$ cicli $c_1,\dots ,c_r$ di $S_n$ sono a supporti disgiunti.

Per esempio $(12),(34)$ sono a supporti disgiunti.

Teorema - Decomposizione di permutazione

Ogni $\sigma \in S_n$ può essere decomposto in prodotto di cicli a supporti disgiunti. Inoltre, tali cicli sono unicamente determinati e commutano tra loro. (C’è analogia tra i cicli e i numeri primi nel TFA).

Esempio

$$\sigma =\left(\begin{array}{cccccccc}1& 2& 3& 4& 5& 6& 7& 8\\ 2& 4& 6& 7& 3& 8& 1& 5\end{array}\right)$$

Estraiamo i cicli, partiamo da un elemento ad esempio 1:

$$1\to 2\to 4\to 7\to 1=(\underset{\text{Orbita}}{\underbrace{1247}})$$

Questo ciclo muove solo questi elementi, troviamone altri quindi partendo da altri elementi non appartenenti all’orbita.

$$3\to 6\to 8\to 5\to 3=(3685)$$

I due cicli sono disgiunti e il loro prodotto commutativi ci restituisce $\sigma$:

$$(1247)(3685)=(3685)(1247)=\sigma$$

---

Sia $G$ gruppo in notazione moltiplicativa e $H<G$, introduciamo una relazione su $G$:

$$x,x^{\prime }\in Gx\sim x^{\prime }\iff x(x^{\prime }{)}^{-1}\in H$$

Lemma: ~ è di equivalenza

Dimostrazione

• Riflessività

$$H<G\Rightarrow 1_G\in H\text{ ma }{1}_G=x{x}^{-1}\forall x\in G\text{ quindi }x\sim x$$

• Simmetria

$$\begin{array}{rl}& x\sim x^{\prime }\iff x(x^{\prime }{)}^{-1}\in H\\ & \text{Ma }\forall h\in H,h^{-1}\in H\\ & \text{Quindi }(x(x^{\prime }{)}^{-1}{)}^{-1}=x^{\prime }{x}^{-1}\in H\end{array}$$

• Transitività

Supponiamo $x$ ~ $x^{\prime }$ e $x^{\prime }$ ~ $x^{\prime \prime }$ allora $x(x^{\prime }{)}^{-1},x^{\prime }(x^{\prime \prime }{)}^{-1}\in H$. Se $a,b$ appartengono al sottogruppo allora ne fa parte anche il loro prodotto e quindi:

$$x(x^{\prime }{)}^{-1}{x}^{\prime }(x^{\prime \prime }{)}^{-1}=x(x^{\prime \prime }{)}^{-1}\in H$$

Domanda

È possibile costruire su $G/\sim$ un’operazione binaria in modo tale che $G/\sim =G/H$ acquisisca una struttura di gruppo? Talvolta si, talvolta no, quali sono le condizioni?

Vorremmo che questa identità fosse valida per la nuova operazione:

$$[x]\circ [x^{\prime }]=[x\cdot x^{\prime }]\text{ Indipendentemente dai rappresentanti}$$

Dove $\circ$ indica la nuova operazione mentre $\cdot$ la vecchia operazione di $G$.

Supponiamo:

$$\begin{array}{rl}& x\sim y\iff [x]=[y]\iff x(y{)}^{-1}\in H\\ & x^{\prime }\sim y^{\prime }\iff [x^{\prime }]=[y^{\prime }]\iff x^{\prime }(y^{\prime }{)}^{-1}\in H\end{array}$$

Ci serve che $[x{x}^{\prime }]=[y{y}^{\prime }]$ ovvero che $x{x}^{\prime }(y{y}^{\prime }{)}^{-1}\in H$ ma notiamo che:

$$x{x}^{\prime }(y{y}^{\prime }{)}^{-1}=x\underset{\in H}{\underbrace{x^{\prime }{y}^{\prime -1}}}{y}^{-1}$$

E questo suggerisce una definizione.

Definizione Sottogruppo Normale

$H$ è un sottogruppo normale di $G$ se $\forall x\in G,xH=Hx$ e si scrive $H◃G$

Condizioni Equivalenti

1. $H◃G$
2. $\forall g\in G$ e $h\in H$, $\exists h^{\prime }\in Ht.c.gh=h^{\prime }g$
3. $\forall g\in G,H^g=H$

Ci basta mostrare che $3\Rightarrow 1\Rightarrow 2\Rightarrow 3$

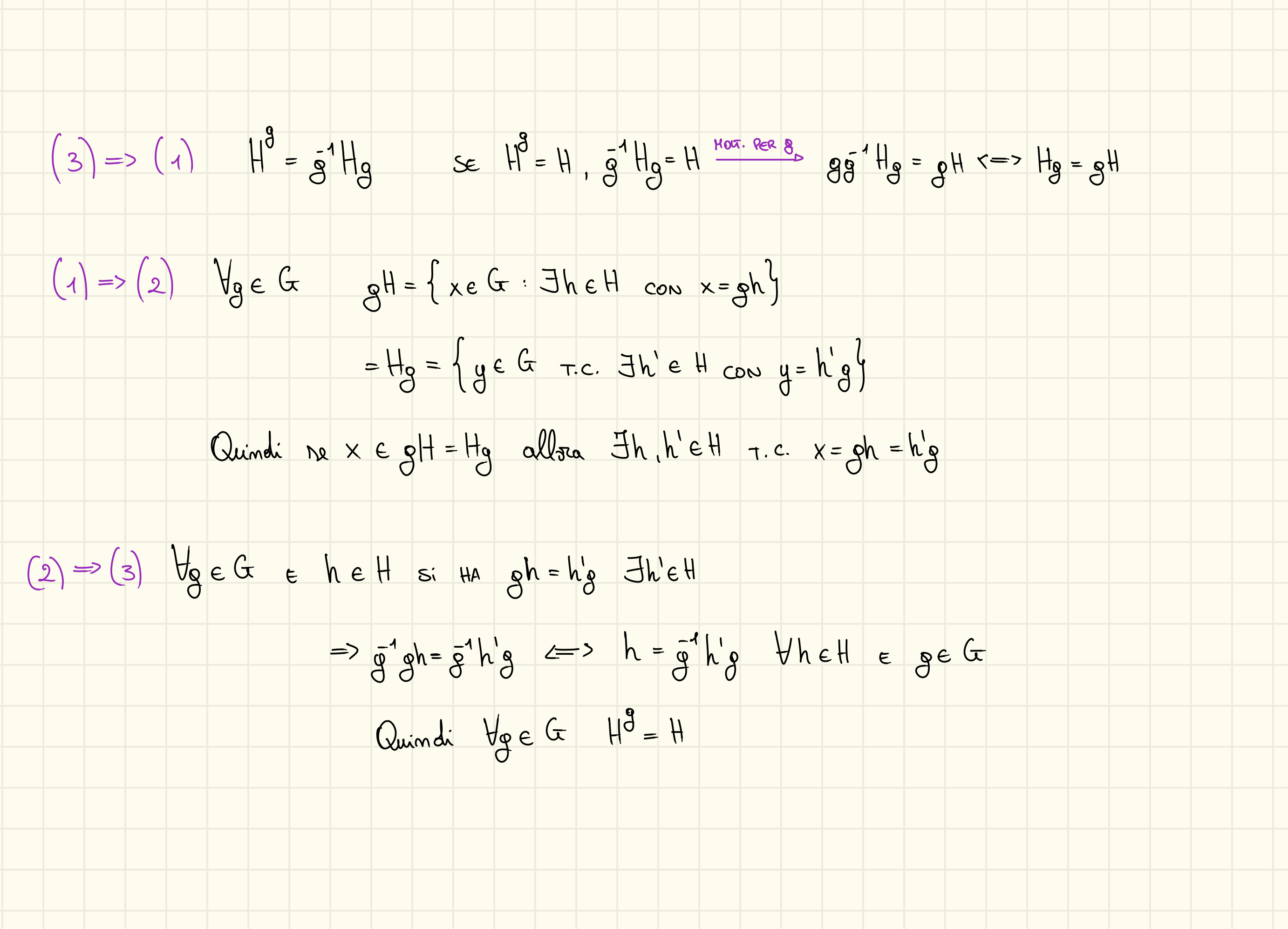
Osservazione

Se $G$ abeliano e $H<G$ allora $H◃G$, tutti i sottogruppi di un gruppo abeliano sono normali.

Inoltre dato $G$ qualsiasi ho $G◃G$ infatti $\forall x\in G,xG=GxeG/G=\{G\}$; e anche $\{1_G\}◃G$ infatti $\forall x\in G,x{1}_G=1_{G}x=x$ e $G/\{1_G\}=\{\{g\}:g\in G\}$.

Tornando all’operazione di prima:

$$x{x}^{\prime }(y{y}^{\prime }{)}^{-1}=x\underset{\in H}{\underbrace{x^{\prime }{y}^{\prime -1}}}{y}^{-1}=xh{y}^{-1}=h^{\prime }\underset{\in H}{\underbrace{x{y}^{-1}}}\in H$$

Quindi $[x{x}^{\prime }]=[y{y}^{\prime }]$ e in questo caso possiamo definire su $G/$~ l’operazione $[x]\cdot [x^{\prime }]:=[x{x}^{\prime }]$

Teorema

Dati $H◃G$ e ~ di equivalenza, allora l’operazione su $G/$~ $[x][x^{\prime }]=[x{x}^{\prime }]$ definisce una struttura di gruppo su $G/$~.

Si scrive $G/H=G/$~ gruppo quoziente di G per H, l’elemento neutro è $1_{G/H}=H$

Lemma

L’applicazione:

$$\begin{array}{r}G\stackrel{{\pi }_H}{\to }{G}_H\\ g\to [g]\end{array}$$

È un omomorfismo di gruppi suriettivo.

Dimostrazione

La suriettività di ${\pi }_H$ è chiara, perché ogni classe contiene un rappresentante inoltre:

$${\pi }_H(g(g^{\prime }{)}^{-1})=[g(g^{\prime }{)}^{-1}]=[g][(g^{\prime }{)}^{-1}]={\pi }_H(g){\pi }_H(g^{\prime }{)}^{-1}$$

Osserviamo inoltre $[g]=gH=Hg$

Infatti $g^{\prime }\in [g]\iff g^{\prime }{g}^{-1}\in H\iff g^{\prime }\in Hg$

Gli elementi di $G/H$ (sottoinsieme di G) sono le classi laterali di H

Lemma

Data $G_1\stackrel{f}{\to }{G}_2$ omomorfismo di gruppi allora $\underset{{=}^{\prime }{H}^{\prime }}{\underbrace{Ker(f)}}◃G_1$ inoltre se $H◃G_1$ allora $H=Ker({\pi }_H)$

Dimostrazione

Se $h\in G_1$ tale che $f(h)=1_{G_2}$ ($\iff h\in Ker(f)$) mostriamo che $\forall x\in G,Ker(f{)}^x=Ker(f)$.

Allora si ha $\forall x\in G_1$:

$$\begin{array}{rl}& f(x^{-1}hx)=f(x^{-1})f(h)f(x)\\ & =f(x{)}^{-1}1G_{2}f(x)\\ & =f(x{)}^{-1}f(x)=1G_2\\ & \iff x^{-1}hx\in Ker(f)\forall h\in Ker(f),\forall x\in G\iff Ker(f{)}^x=Ker(f)\end{array}$$

Se $H◃G$ poniamo $f={\pi }_H$, mostriamo che $H=Ker({\pi }_H)$. Ma se $y\in G$ soddisfa:

$${\pi }_H(g)=1_{G/H}=H\iff gH=H\iff g\in H$$

---

/ff

Prendeteli da Aglaia