Il limite stretto asintotico e la notazione Θ Theta

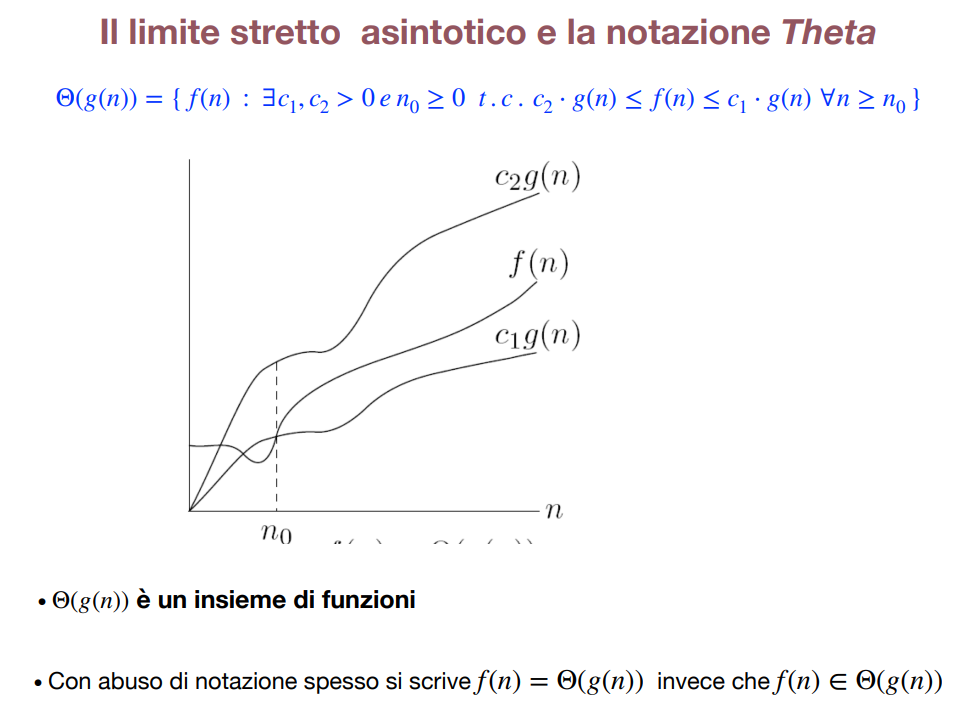
Date due funzioni asintoticamente positive $f(n)$ e $g(n)$ si dice che $f(n)$ è in $\Theta (g(n))$ se esistono tre costanti $c_1,c_2>0$ e $n_0\ge 0$ tali che $c_{1}g(n)\le f(n)\le c_{2}g(n)$ per ogni $n\ge n_0$ Quindi in $\Theta (g(n))$ troviamo tutte le funzioni che hanno lo stesso ordine asintotico di $g(n)$.

Esempio: Prova che

${\log }_{a}n\in \Theta ({\log }_{b}n)$

per ogni $a,b>1$

Ricordiamo che $f(n)\in \Theta (g(n))$ se il limite per $n\to +\infty$ del rapporto $\frac{f(n)}{g(n)}=k$ con $k$ costante diversa da zero. Nel nostro caso otteniamo:

${\lim }_{x\to +\infty }\frac{f(n)}{g(n)}={\lim }_{x\to +\infty }\frac{{\log }_{a}n}{{\log }_{b}n}$

Applicando il cambio di base dei logaritmi otteniamo che

${\log }_{a}n=\frac{{\log }_{b}n}{{\log }_{b}a}$

Quindi:

${\lim }_{x\to +\infty }\frac{{\log }_{b}n}{{\log }_{b}a}\ast \frac{1}{{\log }_{b}n}={\lim }_{x\to +\infty }\frac{1}{{\log }_{b}a}=\frac{1}{{\log }_{b}a}$

Ovvero una costante maggiore di 0

Cambio di base

Il cambio di base è dunque asintoticamente irrilevante ed è per questo che nella notazione asintotica la base del logaritmo viene spesso omessa e si scrive ad esempio semplicemente ${\log }_{a}n\in \Theta (\log n)$.