Esistono diversi tipi di algoritmi di ordinamento alcuni di questi sono molto semplici ma per migliorare l’efficienza dovremo pensare a cose più complesse:

Algoritmi semplici:

Selection Sort
Insertion Sort
Bubble Sort

Algoritmi più complessi:

Mergesort
Quicksort
Heapsort

Selection Sort

Seleziona iterativamente l’elemento più piccolo dell’array non ordinato e lo sposta nella posizione corretta dell’array ordinato.

Una possibile implementazione è:

def SelectionSort(A):
	n = len(A)
	for i in range(n-1):
		min = i
		for j in range(i+1, n):
			if A[j] < A[min]:
				min = j
		A[i], A[min] = A[min], A[i]

Questo algoritmo non ha distizione tra caso migliore e peggiore e abbiamo un costo computazionale di $θ (n^{2})$ .

Insertion Sort

Abbiamo l’array diviso in due parti una ordinata e una non, l’algoritmo prende un elemento dalla parte non ordinata, lo sposta nella parte ordinata e le confronta con tutti gli elementi ordinati fino a che non trova la sua posizione corretta.

Possibile implementazione:

def InsertionSort(A):
	n = len(A)
	for i in range(1, n):
		x = A[i]
		j = i-1
		while j>=0 and A[j]>x:
			A[j+1] = A[j]
			j -= 1
		A[j+1]=x

Nel caso di una lista già ordinata abbiamo una complessità di $θ (n)$

In un caso generale abbiamo una complessità di $θ (n^{2})$

Bubble Sort

Controlla gli elementi due a due partendo da destra e ordinandoli, quindi alla prima “passata” avremo sistemato l’elemento maggiore, alla seconda il precedente al maggiore e così via fino a quando non avremo ordinato la lista.

Possibile implementazione:

def BubbleSort(A):
	n = len(A)
	for i in range(n-1):
		for j in range(n-i-1):
			if A[j] > A[j+1]:
				A[j],A[j+1] = A[j+1],A[j]

Non abbiamo distinzioni per casi migliori o peggiori, in ogni caso abbiamo un costo computazionale di $θ (n^{2})$

La complessità dell’ordinamento

Come facciamo a stabilire un limite sotto al quale nessun algoritmo di ordinamento basato su confronti fra coppie di elementi possa andare?

Possiamo utilizzare uno strumento chiamato albero di decisione che permette di rappresentare tutte le strade che la computazione di un algoritmo può intraprendere. Per gli algoritmi di ordinamento basati sui confronti, ogni test può prendere due strade, minore o maggiore. Quindi un albero di decisione relativo ad un algoritmo di ordinamento basato su confronti ha queste proprietà:

É un albero binario che rappresenta tutti i confronti possibili
Ogni nodo rappresenta un confronto e i figli gli esiti
Ogni foglia rappresenta una possibile soluzione del problema la quale è una permutazione della sequenza in ingresso

Il percorso che facciamo dalla radice alla foglia rappresenta l’esecuzione dell’algoritmo e la lunghezza di tale cammino rappresenta il numero di confronti necessari. Il percorso più lungo rappresenta il caso peggiore.

Cerchiamo quindi di capire se possiamo trovare una limitazione peggiore Dato che come soluzione abbiamo una possibile permutazione della sequenza in ingresso, l’albero deve contenere nelle foglie tutte le permutazioni possibili che per un problema di $n$ elementi sono $n!$ . Inoltre un albero di altezza $h$ non può contenere $2^{h}$ foglie.

Quindi possiamo dire che l’altezza $h$ di un qualunque albero di questo tipo deve essere:

2^{h} \geq n!; h \geq l o g_{2} (n!)

Che in notazione asintotica vale a dire $\ohm (n l o g n)$ .

Costo Computazionale di un ordinamento basato su confronti

Il costo computazionale di un qualunque algoritmo di ordinamento basato su confronti è $\ohm (n l o g n)$

Merge Sort

È un algoritmo ricorsivo che adotta la tecnica divide et impera ovvero:

Divide il problema in sottoproblemi
Risolve i sottoproblemi ricorsivamente
Combina le soluzioni per risolvere il problema originale

Nello specifico il merge sort funziona nel seguente modo:

Divide la sequenza di $n$ elementi in due sottosequenze da $\frac{n}{2}$ elementi
Ordina ricorsivamente le sottosequenze
La ricorsione termina quando la sottosequenza è costituita da un solo elemento e quindi è già ordinata
Le due sottosequenze ormai ordinate vengono fuse in un’unica sequenza ordinata

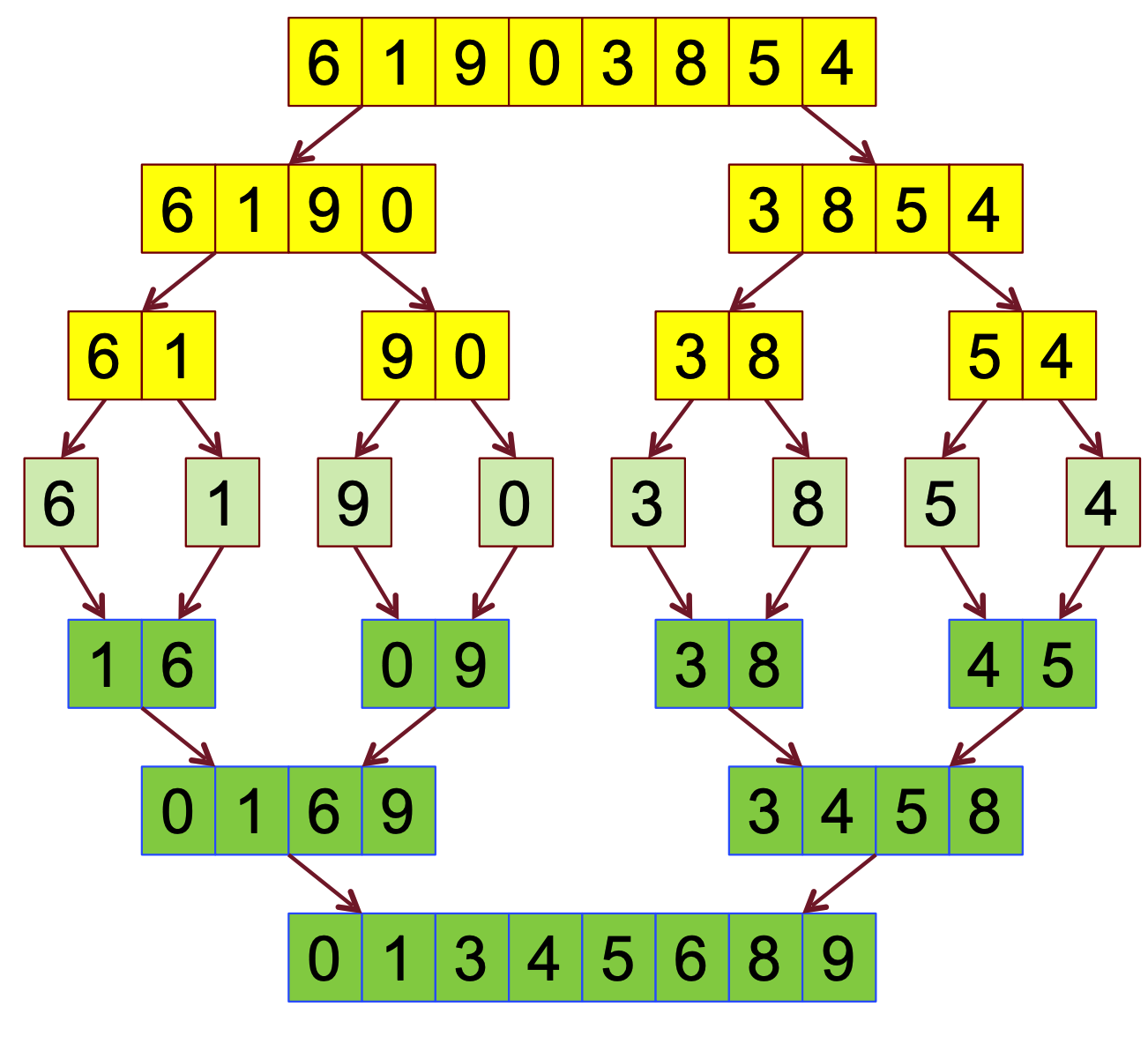
Per scrivere un codice abbiamo bisogno di due funzioni, la funzione Merge_Sort che spezza in due le sequenze e si occupa quindi della ricorsione e la funzione Fondi che unisce due sequenze ordinate

Esempio Codice

def Merge_Sort(A, i, j):
	if i < j:
		m = (i + j) // 2         # Costo 1
		Merge_Sort(A, i, m)      # Costo n/2
		Merge_Sort(A, m + 1, j)  # Costo n/2
		fondi(A, i, m, j)        # Costo di fondi S(n)

Quindi abbiamo una complessità di:

T (n) = θ (n /2) + S (n) T (1) = θ (1)

La funzione fondi si basa sul fatto che le due sottosequenze sono ordinate, inizia a unire gli elementi delle due sequenze scegliendo il minimo fra i due e poi continuando con il prossimo minimo sugli elementi rimanenti delle due sottosequenze, infine copierà gli elementi della lista non terminata.

def fondi(A, i, m, j):
	a, b = i, m+1
	B = []
	while a <= m and b <= j:
		if A[a] <= A[b]:
			B.append(A[a])
			a += 1
		else:
			B.append(A[b])
			b += 1
	while a <= m: # La prima sottolista non è terminata
		B.append(A[a])
		a += 1
	while b <= j: # La seconda sottolista non è terminata
		B.append(A[b])
		b += 1
	for x in range(len(B)): # Ricopio in A gli elementi in B
		A[i+x] = B[x]

Costo di fondi

Il primo ciclo while varia da un minimo di $n /2$ a $n$ quindi è $θ (n)$
Il secondo e il terzo non vengono mai eseguiti entrambi e in ogni caso si ricopia in B gli eventuali elementi rimanenti quindi $O (n)$
Nell’ultimo for copiamo il vettore B in A, quindi $θ (n)$ Costo Totale:

S (n) = θ (1) + θ (n) + O (n) + θ (n) = θ (n)

Costo totale Merge Sort

$T (n) = 2 T (n /2) + θ (n) T (1) = θ (1) T (n) = θ (n l o g n)$

Spazio e Tempo

L’operazione di fusione non si può effettuare senza creare un nuovo vettore B senza incorrere in un aumento del costo. Infatti se vogliamo fare spazio al nuovo minimo dovremmo spostare tutta la sequenza ordinata che costerebbe $θ (n)$ per ciascun elemento da ordinare che porterebbe la nostra equazione di ricorrenza a:
$T (n) = 2 T (n /2) + θ (n^{2}) T (1) = θ (1) T (n) = θ (n^{2})$
Risparmiamo quindi memoria ma non tempo

QuickSort

L’algoritmo di quicksort ha costo $O (n^{2})$ nel caso peggiore ma spesso è la soluzione migliore per grandi valori di $n$ perché il suo tempo di esecuzione medio è $θ (n l o g n)$ e permette un ordinamento in loco quindi con poco utilizzo di memoria. Anche il quicksort è ricorsivo con la tecnica divide et impera, nello specifico funziona nel seguente modo:

Nella sequenza di $n$ elementi si selezione un pivot nella sua giusta posizione in modo da ottenere due sottosequenze, quella degli elementi minori o uguali al pivot e quella degli elementi maggiori.
Le due sottosequenze vengono ordinate ricorsivamente
La ricorsione termina quando le sottosequenze sono formate da un solo elemento
Non occorre combinare i risultati dato che viene effettuata in loco

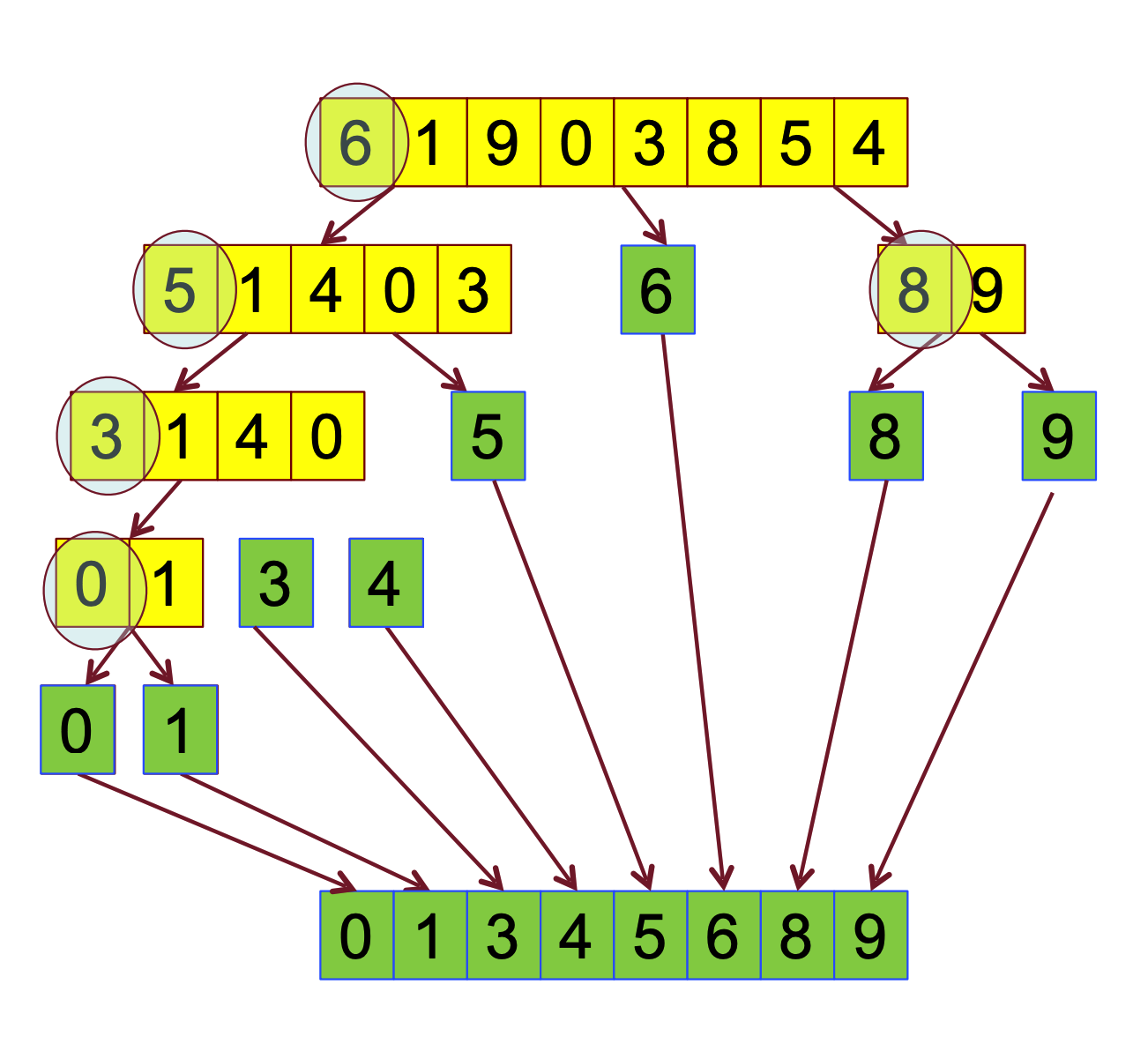
Pseudocodice

def Quick_sort(A, i, j):
	if i < j:
		p = Partition(A, i, j)
		Quick_sort(A, i, p - 1)
		Quick_sort(A, p + 1, j)

In questa implementazione utilizziamo una funzione Partition che sceglie nel sottovettore di A che va dalla posizione $i$ alla posizione $j$ un elemento detto pivot e posiziona tutti gli elementi in modo che a sinistra ci siano i minori o uguali e a destra i maggiori o uguali. In questo modo il pivot si trova nella posizione corretta e tutto questo viene svolto senza utilizzare spazio ausiliario, la funzione restituisce la posizione del pivot.

def partition(A, a, b):
	pivot = A[a] # Seleziona il pivot
	i = a + 1 # Inizializza il punto di divisione
	for j in range(a+1,b+1):
		if A[j] < pivot:
			A[j], A[i] = A[i], A[j]
			i += 1
	A[a], A[i-1] = A[i-1], A[a]
	# Posizionati tutti gli elementi
	return i-1 # Restituisce posizione del pivot

Sia $n$ la porizione di array da partizionare, la complessità di Partition è $θ (n)$

T (n) = T (k) + T (n - 1 - k) + θ (n) T (1) = θ (1) dove 0 \leq k < n

Il caso peggiore è quindi quando il vettore è composto da elementi distinti già ordinati in modo crescente o decrescente mentre il caso migliore si verifica quando ad ogni passo la dimensione dei due sotto-problemi è identica.

Caso Migliore: $θ (n l o g n)$ Caso Peggiore: $θ (n^{2})$

Heap Sort

L’algoritmo di Heap Sort ha un costo computazionale di $O (n l o g n)$ anche nel caso peggiore e ordina in loco senza utilizzare memoria aggiuntiva. Sfrutta una struttura dati chiamata Heap.

Supponiamo di avere una lista $A$ di $n$ elementi su cui nel tempo dovremo effettuare un certo numero di determinate operazioni:

Estrazione del Minimo
Aggiunta di un Elemento

Per la struttura dati Heap abbiamo questo costo delle operazioni:

Crea struttura → $θ (n)$
Estrazione del minimo → $O (l o g ∣ n ∣)$
Aggiunta di un elemento → $O (l o g ∣ n ∣)$

Vedremo successivamente il motivo dietro questi costi e come funziona nello specifico la struttura dati.

In Python la struttura Heap viene implementata con la libreria heapq che ci mette a disposizione alcuni metodi:

heapify(A): Crea la struttura prendendo come parametro una lista
heappop(A): Rimuove e restituisce l’elemento minimo della lista e ristabilisce le proprietà della struttura heap
heappush(A,x): Inserisce l’elemento $x$ in modo che l’heap mantenga le sue proprietà

L’algoritmo di Heap Sort si basa sull’organizzare gli elementi in A come un heap minimo, estrarre gli elementi uno alla volta ed accodarli ad un nuovo vettore B, restituire il vettore B. Ad ogni estrazione infatti si estrae da A il valore minimo quindi in B gli elementi verranno aggiunti in ordine crescente.

def Heapsort(A):
	from heapq import heapify, heappop
	heapify(A) #O(n)
	B = []
	while A: # Eseguito n volte
		B.append(heappop(A)) #O(logn)
	return B

Quindi abbiamo un costo totale di $T (n) = O (n) + θ (n) * O (l o g n) = O (n l o g n)$ .

La struttura dati Heap

Nell’algoritmo abbiamo utilizzato i metodi proposti dalla libreria heapq senza vedere la loro implementazione e senza conoscere le proprietà della struttura dati heap, vediamo ora come funziona.

Cosa succede ad una lista quando viene trasformata in heap

import heapq
A = [12,3,8,4,18,16,11,15,17,10,1]
heapq.heapify(A)
print(A)
# [1,3,8,4,10,12,14,11,15,17,18,16]

Notiamo che la lista è semi - ordinata, infatti nella struttura heap i valori vengono ordinati per rispettare una forma debole di ordinamento chiamata ordinamento verticale, questo significa che guardando gli elementi come se fossero in un albero binario i nodi presenti in ogni cammino radice-foglia risultano ordinati in modo crescente. In questo modo l’elemento minimo si troverà sempre alla radice.

In generale:

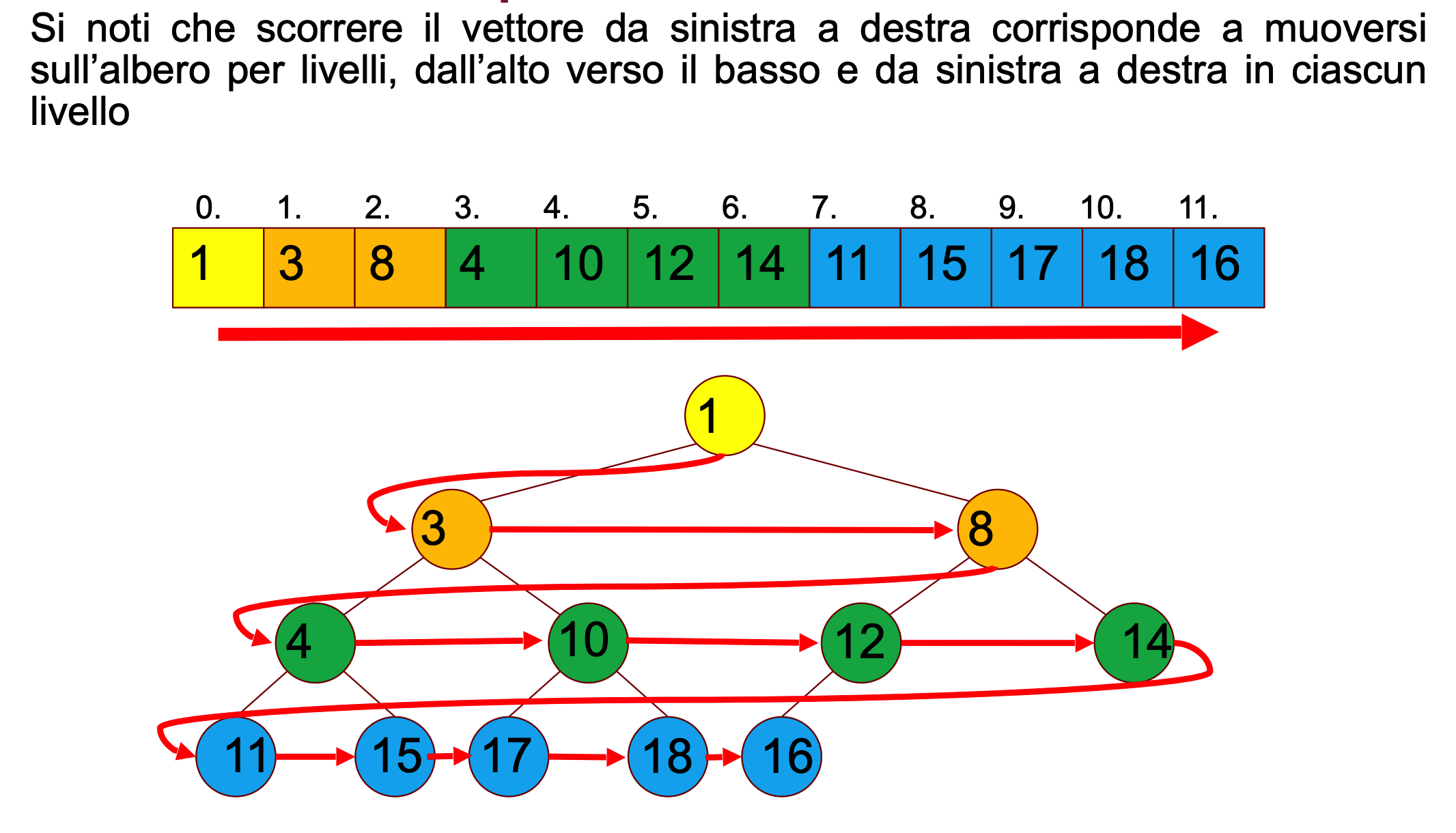
Ogni nodo rappresenta un valore della lista
La radice corrisponde ad A[0]
Il figlio sinistro del nodo A[i], se esiste, corrisponde all’elemento A[2i+1] mentre il figlio destro a A[2i+2]
Il padre del nodo A[i] corrisponde all’elemento $A [∣ \frac{i - 1}{2} ∣]$

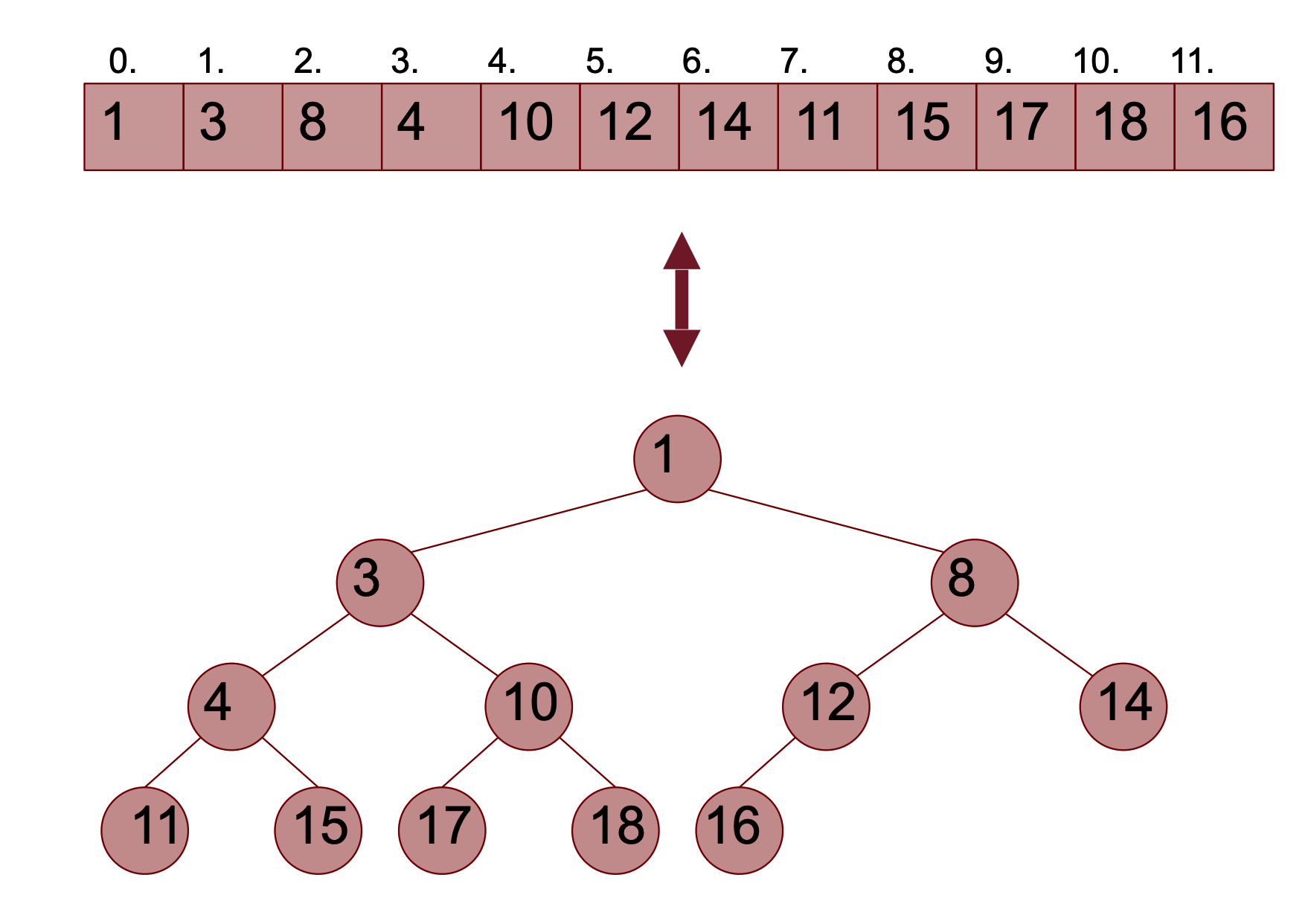
Quindi ogni nodo padre deve essere più piccolo dei figli

Heap minimo e Heap massimo

In questo caso stiamo utilizzando un heap minimo dove la radice è l’elemento minimo e ogni nodo deve essere più piccolo dei suoi figli, esiste anche la struttura heap massimo dove alla radice troviamo il valore più grande e quindi ogni nodo deve essere più grande dei suoi figli

Proprietà:

Siccome tutti i livelli sono pieni tranne al più l’ultimo la sua altezza è $l o g n$
Per ogni nodo vale che i suoi figli sono più grandi di lui
L’elemento minimo si trova sempre alla radice quindi possiamo trovarlo in tempo $θ (1)$

Funzioni di heapq

Funzione Heapify L’algoritmo di heapify si avvale di un’altra funzione heapify1 che ha lo scopo di mantenere le proprietà dell’heap, sotto l’ipotesi che nell’albero su cui viene eseguita sia garantita la proprietà eccette che per la radice. La funzione infatti opera sulla radice confrontandola con i figli e posizionandola al posto giusto in modo ricorsivo

Esempio Funzionamento

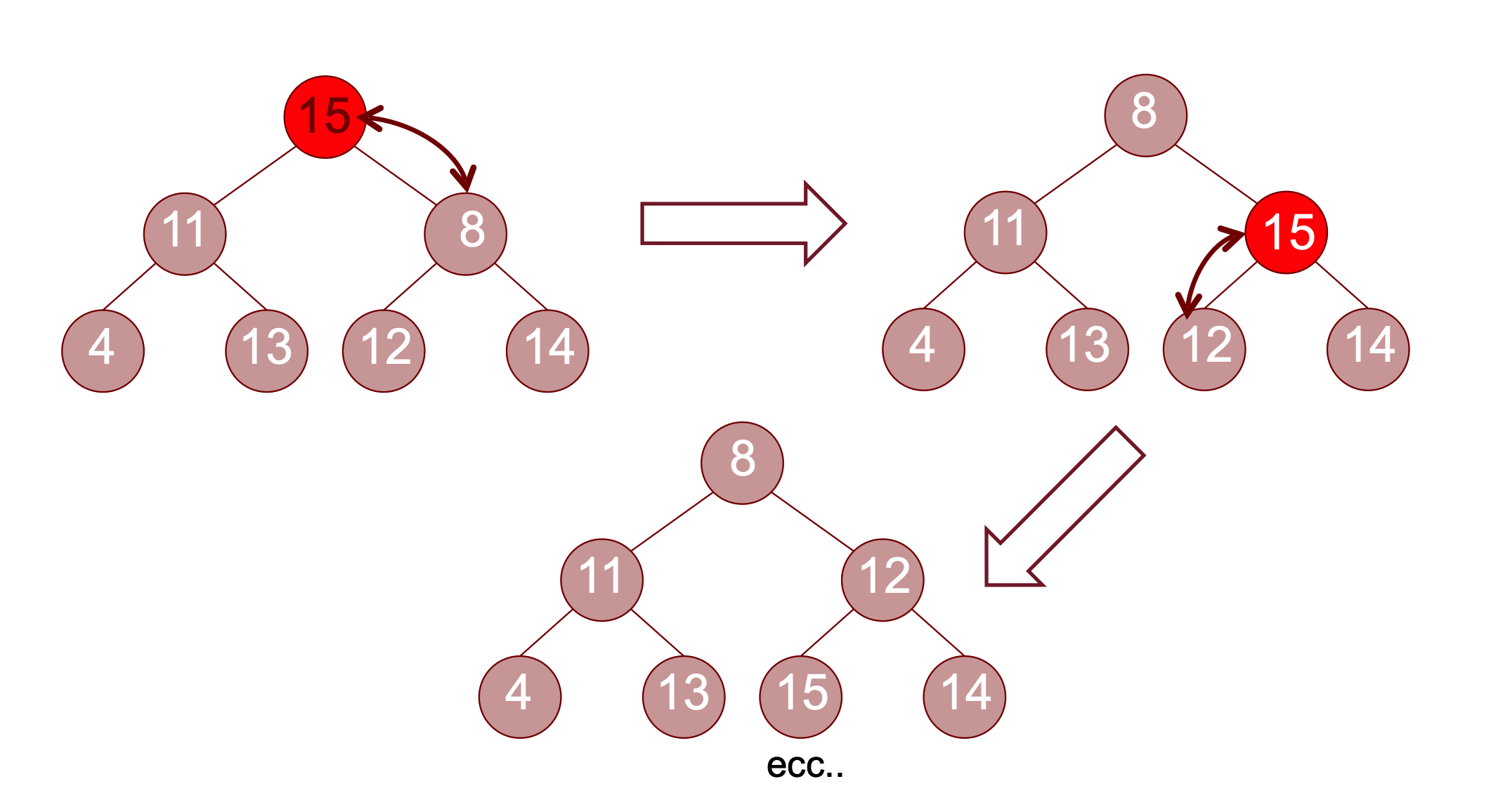
Codice

def Heapify1(A, i):
	n = len(A)
	L = 2*i + 1
	R = 2*i + 2
	indice_min = i
	if L < n and A[L] < A[indice_min]:
		indice_min = L
	if R < n and A[R] < A[indice_min]:
		indice_min = R
	if indice_min != i:
		A[i], A[indice_min] = A[indice_min], A[i]
		Heapify1(A, indice_min)

Dove tutto ha costo costante tranne la chiamata ricorsiva che ha costo pari al numero di nodi del sottoalbero di i che ha più nodi

Funzione Heapify Serve a trasformare un qualunque vettore A in un heap chiamando ripetutamente heapify1 sugli opportuni nodi.

Poiché heapify1 presuppone che entrambi i sottoalberi della radice siano heap, dobbiamo chiamarla scorrendo l’albero dal basso verso l’alto e quindi sul vettore da destra verso sinistra.
Ogni foglia è già un heap quindi ci basta chiamare heapify a partire dal nodo interno più a destra ovvero il padre del nodo ha posizione $n - 1$ e che quindi avrà posizione $∣ \frac{n - 2}{2} ∣$

def Heapify(A):
	for i in range((len(A)-2)//2, -1, -1):
		heapify1(A, i)

La funzione Heapify effettua non più di $n$ chiamate a Heapify1 che sappiamo avere ciascuna $O (l o g n)$ quindi $T (n) = O (n l o g n)$ ma con opportune dimostrazioni in realtà il cosot è di $T (n) = θ (n)$

Implementazione funzione heappop(A)

Salviamo in una variabile il minimo cioè $A [0]$
Copiamo in $A [0]$ l’ultimo elemento $A [n - 1]$ e cancelliamo l’ultimo
Fuori posto ora abbiamo soltanto la radice che possiamo sistemare chiamando heapify1(A, 0)
Restituiamo la variabile x

def Heappop(A):
	x = A[0]
	A[0] = A[n - 1]
	A.pop()
	Heapify1(A, 0)
	return x

Dove l’unico costo non costante è la chiamata a Heapify1 che sappiamo costare $O (l o g n)$

Implementazione funzione heappush(A, x)

Aggiungiamo l’elemento x all’ultimo posto nell’heap
Facciamo risalire x nell’heap fino a che non risulta maggiore del padre o raggiunge la radice

def Heappush(A, x):
	A.append(x)
	i = len(A) - 1
	while i > 0 and A[i]<A[(i-1)//2]:
		A[i], A[(i-1)//2] = A[(i-1)//2], A[i]
		i = (i-1)//2

La complessità è data dal ciclo while che è $O (l o g n)$ infatti il caso pessimo si ha quando l’elemento da inserire è il minimo e dobbiamo finire quindi alla radice ovvero $θ (h)$ dove $h$ è l’altezza. Poiché l’heap contiene $n$ elementi l’altezza dell’albero binario è $θ (l o g n)$

Ordinamenti Stabili

Un algoritmo di ordinamento si dice stabile se mantiene l’ordine relativo per gli elementi con stessa chiave. Questo significa che se due elementi hanno la stessa chiave, un algoritmo stabile deve garantire che l’elemento che compare prima nella lista non ordinata dovrà comparire prima anche nella lista ordinata.

Ad esempio nel Selection Sort abbiamo un ordinamento non stabile dato che presa una lista $[2, 2, 1]$ se la ordiniamo otteniamo $[1, 2, 2]$ ma il 2 a posizione 0 è finito nell’ultima posizione, questo significa che abbiamo scambiato l’ordine dei 2 rispetto alla lista originale.

Algoritmi stabili:

BubbleSort
InsertionSort
MergeSort
TimSort Algoritmi non Stabili:
SelectionSort
QuickSort
HeapSort

Ordinamenti Lineari

Finora abbiamo utilizzato algoritmi di ordinamento basati su confronti e sappiamo che questi hanno un costo computazionale di $θ (n l o g n)$ , per ottenere degli algoritmi lineari dobbiamo rimuovere l’ipotesi che l’algoritmo sia unicamente basato su confronti.

Counting Sort

Ipotesi: Ciascuno degli $n$ elementi da ordinare è un intero nell’intervallo $[0, \dots, k]$ Idea: Fare in modo che il valore di ogni elemento della sequenza determini direttamente la sua posizione nella sequenza ordinata.

Il costo computazionale è di $θ (n + k)$ . Se $k = 0$ allora l’algoritmo ordina $n$ elementi in tempo lineare.

Quindi nello specifico dobbiamo:

Trovare l’elemento $k$ massimo dell’array $A$ da ordinare
Inizializzare l’array $C$ coni i $k$ contatori delle occorrenze di $A$
Scorrere $A$ e per ogni indice $i$ incrementiamo il contatore alla posizione $C [A [i]]$ delle occorrenze di $A [i]$
Scorriamo $C$ e per ogni indice $i$ inseriamo $C [i]$ occorrenze all’elemento $i$ in $A$

Esempio Grafico:

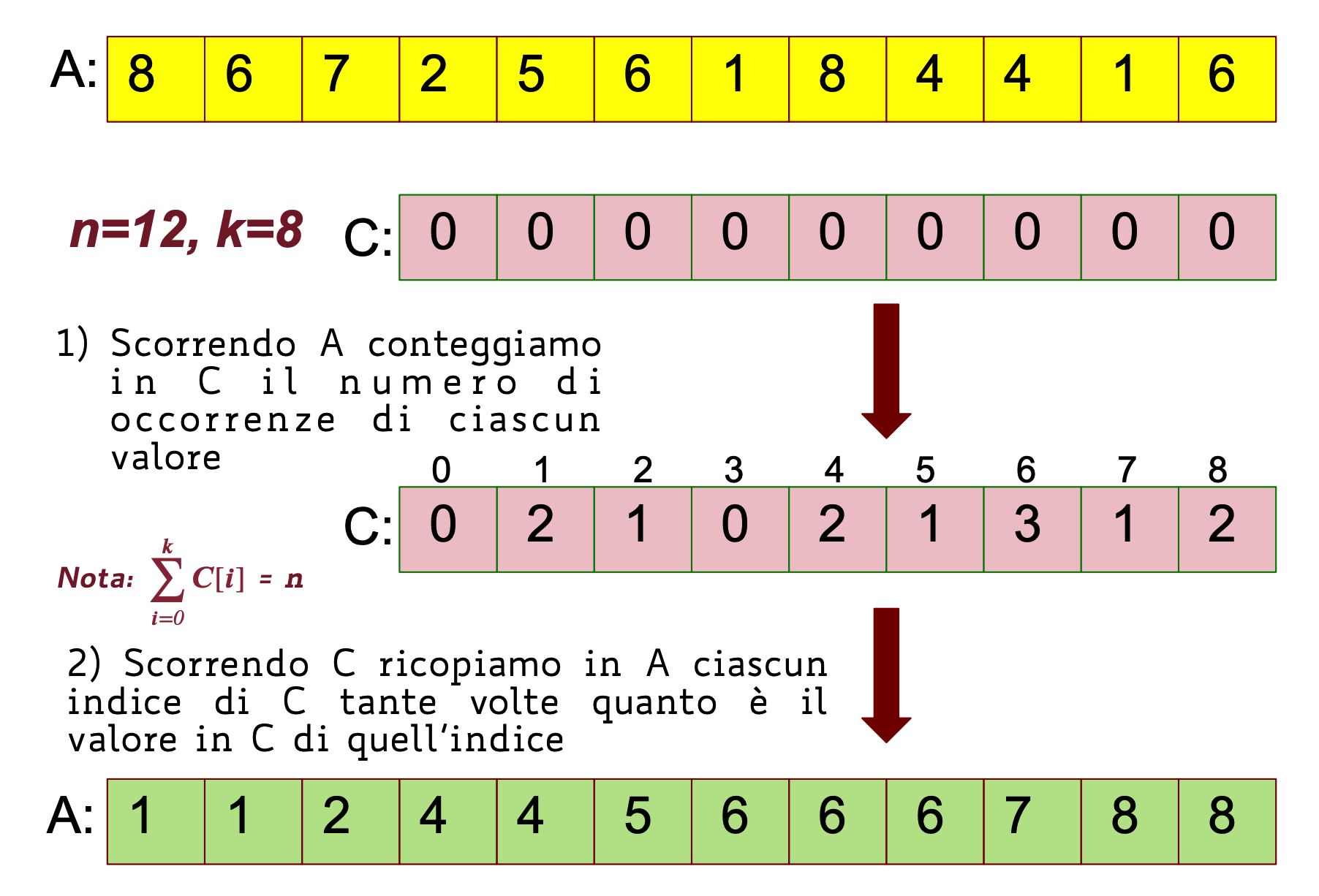
Codice

def Counting_Sort(A):
	k = max(A) # Theta(n)
	n = len(A)
	C = [0] * (k + 1) # Theta(k)
	for i in range(n): # Theta(n)
		C[A[i]] += 1
	j = 0
	for i in range(len(C)): # Eseguito k + 1 volte
		for _ in range(C[i]): # Eseguito C[i] volte
			A[j] = i
			j += 1
	# I due ultimi for vengono eseguiti n volte

Quindi eseguendo le somme asintotiche otteniamo $T (n) = θ (n + k)$

Bucket Sort (k buckets)

Ipotesi: Gli $n$ elementi da ordinare appartengono all’intervallo $[0, \dots, M]$ e non sono necessariamente interi ma equamente distribuiti nell’intervallo. Idea: Dividere l’intervallo $[0, \dots, M]$ in $k$ sottointervalli detti bucket e distribuire i valori nei loro bucket per poi ordinarli separatamente. Un elemento $x$ finisce nel bucket $⌊ k \cdot \frac{x}{M + 1} ⌋$

Il costo computazionale dipenderà dall’algoritmo utilizzato per ordinare i vari buckets ma dato che gli elementi in input sono uniformemente distribuiti non ci si aspetta che molti elementi cadano nello stesso bucket, infatti in ognuno ci saranno circa $\frac{n}{k}$ elementi.

Se prendiamo $k = \frac{n}{c}$ dove $c$ è una opportuna costante allora in ogni bucket ci saranno $\frac{n}{n / c} = c$ elementi e quindi otteniamo un costo di ordinamento pari a $θ (1)$

BucketSort con numero di bucket pari a n

Creiamo una lista di $n$ buckets vuoti
Troviamo $M$ ovvero l’elemento massimo dell’array $A$ da ordinare
Scorriamo $A$ e per ogni valore $x$ inseriamo $x$ nel bucket $B [⌊ n \cdot \frac{x}{M + 1} ⌋]$
Ordiniamo gli elementi di ciascun bucket
Concateniamo gli elementi ordinati dei vari bucket

Esempio Grafico

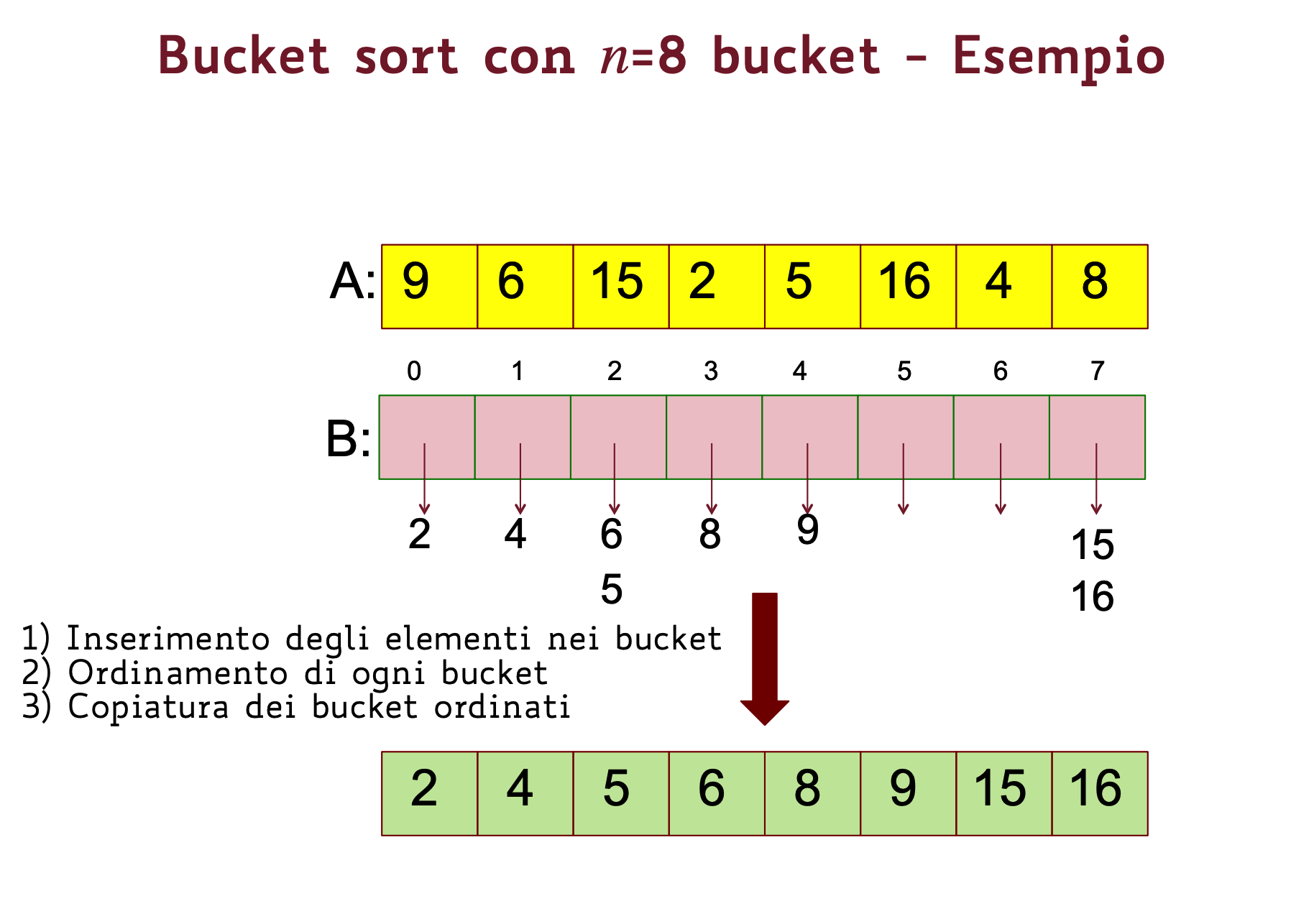
Codice

def Bucket_sort(A):
	# Creo lista di n buckets
	n = len(A)
	B = [[] for _ in range(n)] # Theta(n)
	# Distribuisco gli elementi nei buckets
	M = max(A)
	for x in A: # Theta(n)
		i = n * x // (M+1)
		B[i].append(x)
	# Ordino gli elementi di ogni bucket
	for i in range(n): # Somma dei costi di ord. di ogni bucket
		B[i].sort()
	# Concateno gli elementi dei buckets
	R = []
	for i in range(n): # Somma dei costi di ogni bucket
		R.extend(B[i])
	return R

Quindi otteniamo

T (n) = θ (n) + i = 0 \sum n - 1 θ (costo per ordinare ∣ B [i] ∣ elementi)

Caso Pessimo: Tutti gli elementi finiscono nello stesso bucket. Otteniamo $T (n) = θ (n) + θ (costo per ordinare n elementi)$ e quindi la complessità dipende dall’algoritmo di sort utilizzato.

Caso Ottimo: Gli elementi sono equidistribuiti nell’intervallo $[0, \dots, M]$ e quindi in ogni bucket finiranno $θ (1)$ elementi. $T (n) = θ (n) + θ (costo per ordinare θ (1) elementi)$ e quindi indipendetemente dall’algoritmo di sort otteniamo un costo complessivo di $T (n) = θ (n) + θ (n) \cdot θ (1) = θ (n)$

👨🏻‍💻 Alem's Notes

Il Problema dell'Ordinamento

Selection Sort

Insertion Sort

Bubble Sort

La complessità dell’ordinamento

Merge Sort

QuickSort

Heap Sort

La struttura dati Heap

Funzioni di heapq

Ordinamenti Stabili

Ordinamenti Lineari

Counting Sort

Bucket Sort (k buckets)

BucketSort con numero di bucket pari a n

Table of Contents

Backlinks