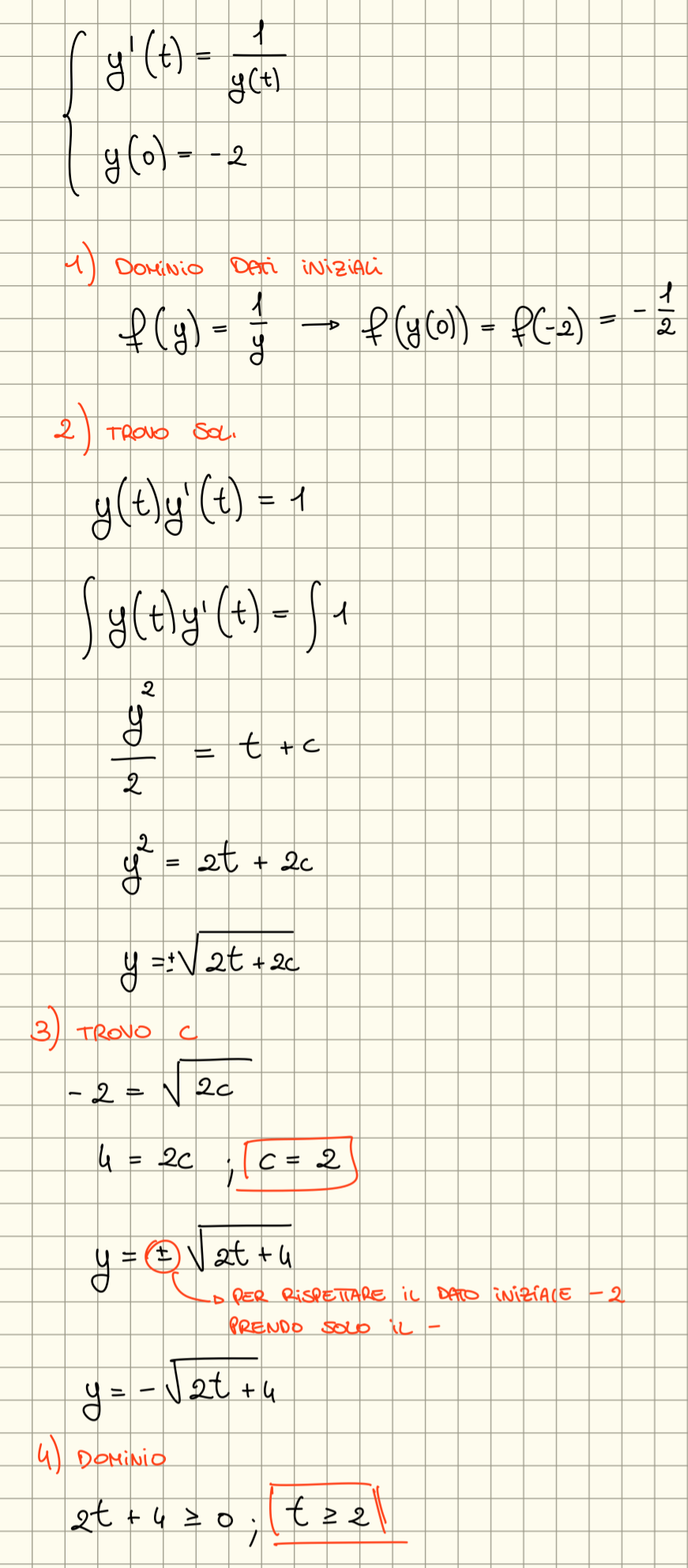Equazioni Differenziali

Le equazioni differenziali sono equazioni dove l’incognita è una funzione e in cui sono presenti una o più derivate della funzione incognita

Esempio

$$f(x)+f^{\prime }(x)=x$$

Dobbiamo quindi trovare una funzione da sostituire con $f(x)$ che soddisfa l’equazione. Quindi in questo caso le soluzioni saranno tutte le funzioni del tipo $y=f(x)$ che sommate alla loro derivata prima danno come risultato $x$. Infatti spesso al posto di $f(x)$ si utilizza la notazione $y,y^{\prime }$:

$$y^{\prime }+y=x$$

Esempio 2

$$f^{\prime \prime \prime }(x)+3f^{\prime \prime }(x)=9x$$

Qui, anche se non compare esplicitamente $f(x)$, compaiono delle sue derivate e dobbiamo comunque trovare una $f(x)$ che rispetti l’equazione. Quindi possiamo scrivere:

$$y^{\prime \prime \prime }+3y^{\prime \prime }=9x$$

E la soluzione è data quindi da tutte le funzioni del tipo $y=f(x)$ la cui derivata terza sommata a 3 volte la derivata seconda danno come risultato $9x$

Ordine

L’ordine di un’equazione differenziale è il massimo ordine di derivazione che compare

Per risolvere le equazioni differenziali non esiste un metodo standard ma bisognerà analizzare caso per caso e trovare il metodo più adatto.

Esempio 3

$$f^{\prime }(x)=x$$

Quindi abbiamo un’equazione differenziale del primo ordine. Per risolverla dobbiamo chiederci, quali sono le funzioni la cui derivata prima è uguale a x?

In questo caso possiamo ad esempio risolvere l’integrale indefinito

$$\int xdx=\frac{x^2}{2}+c$$

per trovare così la famiglia delle primitive che danno come derivata prima $x$, quindi il risultato è l’insieme delle funzioni $\{\frac{x^2}{2}+c\}$, abbiamo ottenuto quindi un insieme di soluzioni che variano in base al parametro $c$.

Esempio 4

Non sempre il risultato è così immediato

$$f^{\prime }(x)=2-\sqrt{f(x)}$$

In questo caso non possiamo utilizzare lo stesso metodo di prima perché otteniamo un calcolo come questo:

$$f(x)=\int f^{\prime }(x)dx=\int [2-\sqrt{f(x)}]dx$$

Ma per calcolare questo integrale dobbiamo conoscere $f(x)$, impareremo a risolverlo più avanti.

---

Le equazioni differenziali del primo ordine si dividono in diverse categorie:

• Equazioni Differenziali Elementari
• Equazioni Differenziali a Variabili Separabili
• Equazioni Differenziali Lineari

---

Equazioni Differenziali Elementari

Sono quelle equazioni differenziali che possono essere risolte in modo abbastanza immediato

Tipologia 1

$$y^{\prime }=f(x)$$

In questo caso basta integrare:

$$y=\int f(x)dx=F(x)+c$$

Esempio

$$y^{\prime }=3e^{2x}$$

Integriamo:

$$\int 3e^{2x}dx=3\int e^{2x}dx=\frac{3}{2}\int 2e^{2x}dx=\frac{3}{2}{e}^{2x}+c$$

Tipologia 2

$$y^{\prime \prime }=f(x)$$

In questo caso, in modo molto simile a prima ci basta integrare 2 volte:

$$y^{\prime }=\int f(x)dx=F(x)+c$$ $$y=\int F(x)+c_{1}dx=\int F(x)dx+c_{1}x+c_2$$

Esempio

$$\begin{array}{rl}{y}^{\prime \prime }& =2-\cos (x)\\ y^{\prime }& =\int 2-\cos (x)dx=2x-\sin (x)+c_1\\ y& =\int 2x-\sin (x)+c_{1}dx\\ & =\int 2xdx-\int \sin (x)dx+\int c_{1}dx\\ & =2\cdot \frac{x^2}{2}+\cos (x)+c_{1}x+c_2=x^2+\cos (x)+c_{1}x+c_2\end{array}$$

Parametri Soluzione

Se l’equazione differenziale è di ordine $n$ ci aspettiamo infinite soluzioni parametrizzate da $n$ parametri. Infatti nelle equazioni di primo ordine abbiamo ottenuto una sola $c$ mentre in questa equazione di secondo ordine abbiamo ottenuto due parametri $c_1,c_2$ diversi.

Problema di Cauchy

Alcune volte le equazioni differenziali possono essere accompagnate da delle condizioni iniziali, in questi casi ci troviamo davanti ad un problema di Cauchy. Risolvere un problema di Cauchy significa trovare tra le infinite soluzioni dell’equazione differenziale quella che soddisfa le condizioni iniziali.

$$\{\begin{array}{l}{y}^{\prime }=-e^{-x}\\ y(0)=3\end{array}$$

1. Per prima cosa risolviamo l’equazione differenziale come sempre, quindi integrando otteniamo:

$$y=\int -e^{-x}dx=e^{-x}+c$$

2. Sfruttiamo la condizione iniziale per trovare il parametro $c$, quindi sostituendo $y$ e $x$:

$$3=e^{-0}+c\to c=2$$

Quindi la soluzione del problema di Cauchy è:

$$y(x)=e^{-x}+2$$

E non è più un’insieme di infinite soluzioni, ma una funzione soltanto

Esempio

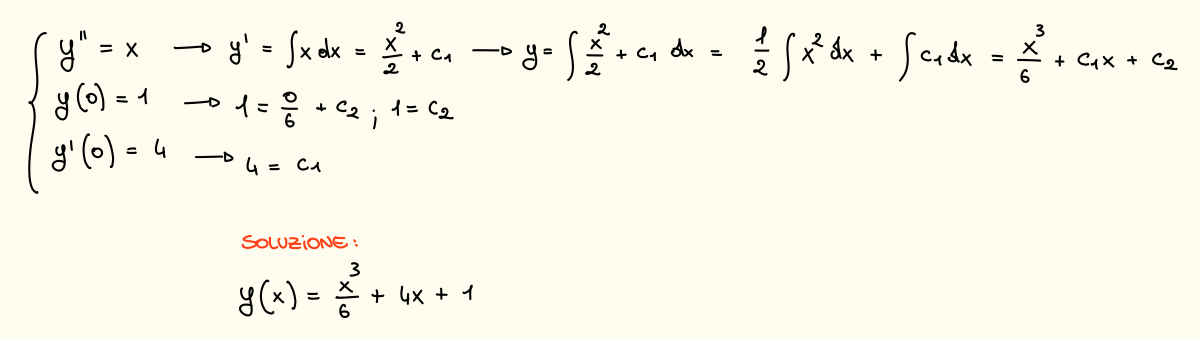
Condizioni e Parametri

Notiamo che il numero di condizioni iniziali deve essere uguale al numero di parametri $c$ che differenziano la nostra funzione, inoltre devono fissare i valori della funzione o sue derivate in uno stesso punto, guardando l’esempio precedente tutte le condizioni fissano le funzioni in $x=0$.

Equazioni Differenziali a Variabili Separabili

Sono equazioni differenziali del primo ordine riconducibili alla seguente forma:

$$y^{\prime }=f(x)\cdot g(y)$$

Esempi

$$y^{\prime }=y\ln x|y^{\prime }=e^{x}y\ln y$$

In entrambi gli esempi compare un “pezzo” in funzione di $y$ un altro in funzione di $x$.

Come si risolvono?

Dobbiamo separare le variabili $x$ ed $y$, integriamo ciascun membro rispetto alla variabile da cui dipende e infine ricaviamo $y(x)$

Esempio 1

Esempio 2

Non sempre è facile eseguire questi passaggi, potrebbe accadere di incontrare qualche integrale più complesso.

Soluzioni Costanti

Come successo nel primo esempio dobbiamo controllare se oltre alle soluzioni trovate l’equazione differenziale ammette soluzioni costanti. Data un’equazione differenziale $y^{\prime }=f(x)\cdot g(y)$ se esiste un numero $\overline{y}$ tale che $g(\overline{y})=0$ allora $y(x)=\overline{y}$ è una soluzione dell’equazione differenziale. Nel primo esempio infatti ponendo $y(x)=0$ azzeravamo il termine a destra rendendo sempre vera l’equazione.

Equazioni Differenziali Lineari del Primo Ordine

Sono tutte quelle equazioni differenziali della forma:

$$y^{\prime }(x)+a(x)\cdot y(x)=f(x)$$

Quindi sono equazioni dove compare la derivata prima più la funzione che vogliamo moltiplicare moltiplicata per una funzione di $x$, tutto questo uguale ad un’altra funzione di $x$.

Esempi

$$y^{\prime }-xy=2x|y^{\prime }+\frac{1}{x}\cdot y=4x^2$$

Notiamo subito due cose:

• Se $a(x)=0$ e quindi non compare nell’equazione ricadiamo in quelle che abbiamo definito equazioni differenziali elementari
• Se $f(x)=0$ cadiamo invece in un’equazione differenziale a variabili separabili

Come si risolvono?

Si utilizza un metodo chiamato fattore integrante:

• Trovo una primitiva di $a(x)$
• Moltiplico entrambi i membri per $e$ elevato alla primitiva $A(x)$ ottenendo quindi $y^{\prime }(x)e^{A(x)}+a(x)e^{A(x)}y(x)=f(x)e^{A(x)}$ e notiamo che nel membro a sinistra abbiamo ottenuto $[y(x)e^{A(x)}{]}^{\prime }$
• Integriamo entrambi i membri e quindi otteniamo:

$$y(x)e^{A(x)}=\int f(x)e^{A(x)}dx+c$$

• Infine ricaviamo $y(x)$ moltiplicando entrambi i membri per $e^{-A(x)}$

$$y(x)=e^{-A(x)}\int f(x)e^{A(x)}dx+c{e}^{-A(x)}$$

Esempio 1

Anche in questo caso i passaggi sono facilmente eseguibili se troviamo integrali non troppo complessi durante il metodo risolutivo.

Equazioni Differenziali del Secondo Ordine a Coefficienti Costanti Omogenee

Si presentano come equazioni differenziali del tipo:

$$a{y}^{\prime \prime }(x)+b{y}^{\prime }(x)+cy(x)=0$$

Dove $a,b,c$ sono numeri Reali.

Le soluzioni di questo tipo di equazioni hanno una particolarità, se prendiamo una soluzione e la moltiplichiamo per una costante otteniamo allora un’altra soluzione dell’equazione e se prendiamo due soluzioni qualsiasi e le sommiamo (anche moltiplicate per altre costanti), la funzione risultato della somma è ancora risultato.

Le soluzioni saranno quindi nella forma:

$$y(x)=c_1{y}_1(x)+c_2{y}_2(x)$$

Quindi le funzioni ci danno la base mentre i parametri $c$ ci torneranno utili per trovare soluzioni uniche nei problemi di Cauchy.

Per trovare la soluzione dobbiamo risolvere nell’insieme dei numeri complessi $\mathbb{C}$ la funzione caratteristica $a{z}^2+bz+c=0$ dove i parametri $a,b,c$ sono li stessi che compaiono nell’equazione differenziale iniziale, essendo un’equazione di secondo grado possono verificarsi 3 casi:

• 2 soluzioni reali e distinte ${\lambda }_1\ne {\lambda }_2$: Allora $y_1(x)$ e $y_2(x)$ saranno uguali, rispettivamente a $e^{{\lambda }_{1}x}$, $e^{{\lambda }_{2}x}$ e quindi abbiamo come soluzione generale:

$$y(x)=c_1{e}^{{\lambda }_{1}x}+c_2{e}^{{\lambda }_{2}x}$$

• 2 soluzioni reali coincidenti ${\lambda }_1={\lambda }_2$: Allora $y_1(x)$ e $y_2(x)$ saranno uguali, rispettivamente a $e^{\lambda x}$, $x{e}^{\lambda x}$ e quindi abbiamo come soluzione generale:

$$y(x)=c_1{e}^{\lambda x}+c_{2}x{e}^{\lambda x}$$

• 2 soluzioni complesse ${\lambda }_{1,2}=\alpha \pm i\beta$: Allora $y_1(x)$ e $y_2(x)$ saranno uguali, rispettivamente a $e^{\alpha x}\cos (\beta x),e^{\alpha x}\sin (\beta x)$ e quindi abbiamo come soluzione generale:

$$y(x)=c_1{e}^{\alpha x}\cos (\beta x)+c_2{e}^{\alpha x}\sin (\beta x)$$

Esempio 1

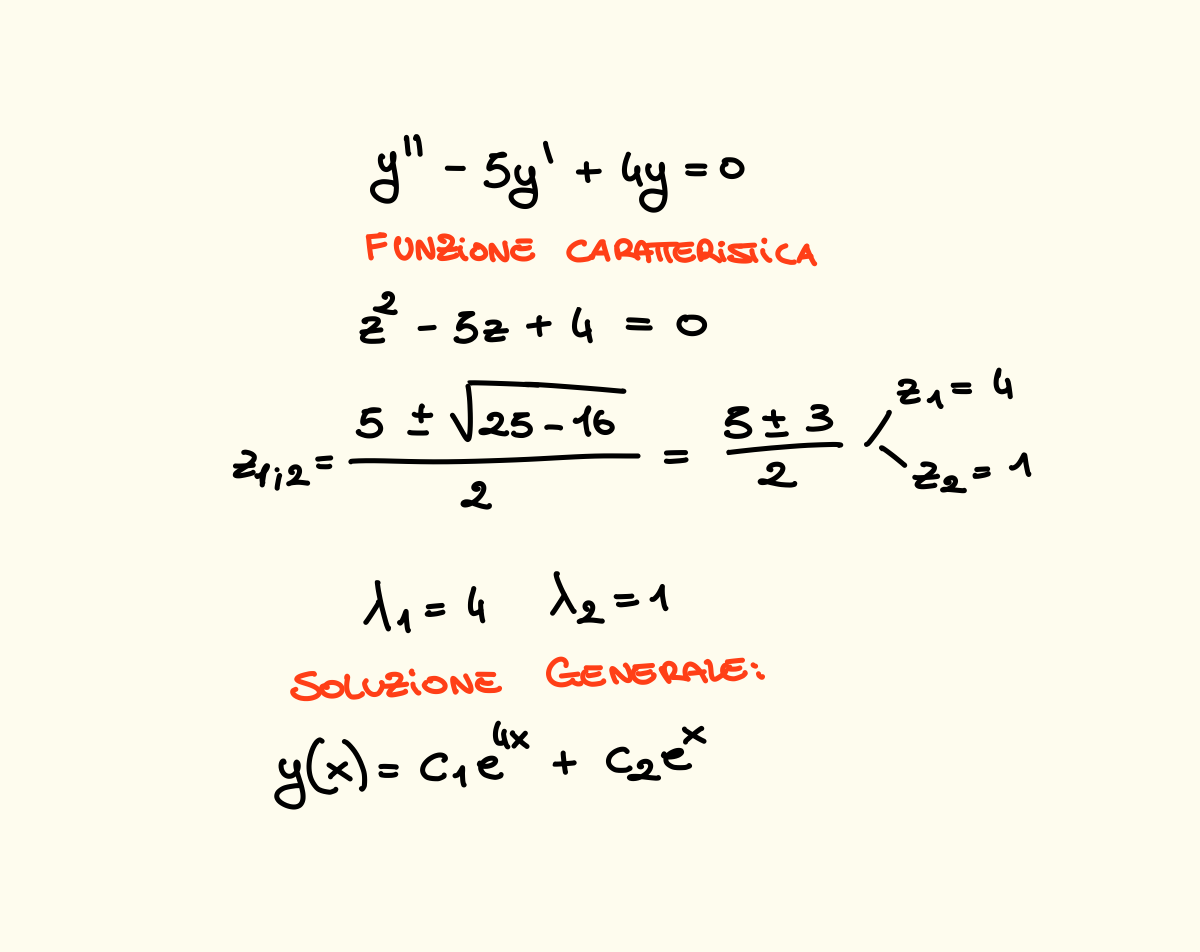
Esempio 2

Equazioni di secondo ordine non omogenee

Sono equazioni del tipo:

$$y^{\prime \prime }(t)+a{y}^{\prime }(t)+by(t)=f(t)$$

$f(t)$ è anche detta forzante.

Per risolvere dobbiamo prima di tutto studiare la sua forma omogenea con gli stessi passaggi che già conosciamo, la soluzione quindi sarà una famiglia di soluzioni parametrizzate da c1 e c2, questa famiglia la chiameremo $y_g(t)$ (generale).

Adesso dobbiamo cercare una soluzione specifica $y_p$ dell’equazione non omogenea, utilizziamo il metodo di somiglianza:

• Se $f(t)$ è un polinomio di grado n cerchiamo una soluzione che sia sempre un polinomio di grado n: Basandoci sulle soluzioni $\lambda$ del polinomio caratteristico individuiamo questi casi:
  • $\lambda =0$ non è soluzione del polinomio caratteristico, allora $y_p$ sarà un polinomio di grado n
  • $\lambda =0$ è soluzione del polinomio caratteristico con molteplicità 1, allora $y_p$ sarà un polinomio di grado n moltiplicato per $t$
  • $\lambda =0$ è soluzione del polinomio caratteristico con molteplicità 2, allora $y_p$ sarà un polinomio di grado n moltiplicato per $t^2$
• Se $f(t)=e^{\alpha t}P(t)$ con $P(t)$ di grado n:
  • Se $\alpha$ non è soluzione del polinomio caratteristico, $y_p=e^{\alpha t}\cdot$ Polinomio di grado n
  • Se $\alpha$ è soluzione di molteplicità 1 del polinomio caratteristico, $y_p=t{e}^{\alpha t}\cdot$ Polinomio di grado n
  • Se $\alpha$ è soluzione di molteplicità 2 del polinomio caratteristico, $y_p=t^2{e}^{\alpha t}\cdot$ Polinomio di grado n
• Se $f(t)=P_m{e}^{\alpha t}\cos (\beta t)+Q_n{e}^{\alpha t}\sin (\beta t)$ con $P_m$ e $Q_n$ polinomi di grado m,n:
  • NOTA: se $\beta =0$ ci troviamo nel caso di prima
  • Se $\alpha \pm i\beta$ non è soluzione del polinomio caratteristico, $y_p=e^{\alpha t}[A(t)\cos (\beta t)+B(t)\sin (\beta t)]$ dove $A,B$ sono polinomi di grado $max(n,m)$.
  • Se $\alpha \pm i\beta$ è soluzione del polinomio caratteristico, $y_p=t{e}^{\alpha t}[A(t)\cos (\beta t)+B(t)\sin (\beta t)]$ dove $A,B$ sono polinomi di grado $max(n,m)$.

Caso Particolare dell’ultimo. Quando $\alpha =0$ e $m=n=0$ abbiamo $f(t)=c_1\cos (\beta t)+c_2\sin (\beta t)$:

• Se $i\beta$ non è soluzione del polinomio caratteristico, $y_p={\gamma }_1\cos (\beta t)+{\gamma }_2\sin (\beta t)$
• Se $i\beta$ è soluzione del polinomio caratteristico, $y_p=t[{\gamma }_1\cos t+{\gamma }_2\sin t]$

Per calcolare i polinomi utilizziamo un’equazione, esempi dopo.

Una volta ottenuta anche una soluzione particolare, per ottenere la soluzione dell’equazione differenziale ci basta sommare la generale alla particolare.

Esempio con f(t) Polinomio

Esempio con f(t) esponenziale per polinomio

Riassunto Esercizi

Per distinguere le equazioni differenziale dobbiamo individuare ordine, linearità, coefficienti, omogenea o non.

Prendiamo ad esempio questa equazione differenziale:

$$y^{\prime }+t^{2}y=0$$

• L’ordine è dato dal grado massimo delle derivate che compaiono, in questo caso quindi è 3
• Si dice lineare se la funzione $y$ non compare come variabile di altre funzioni
• I coefficienti sono i coefficienti che moltiplicano la $y$ quindi possono essere costanti oppure variabili
• Si dice omogenea se = 0 altrimenti non omogenea

Quindi in questo caso abbiamo un’equazione differenziale del primo ordine, lineare, a coefficienti variabili e omogenea.

Metodi Risolutivi 1° Ordine

In tutti i casi, se ho un problema di Cauchy devo sostituire i casi iniziali e ricavare la $c$.

| Coefficienti Costanti Omogenee

$$y^{\prime }(t)+ay(t)=0y(t)=c\cdot e^{-at},c\in \mathbb{R}$$

| Coefficienti Costanti non Omogenee

$$y^{\prime }(t)+ay(t)=f(t)$$

• Moltiplicare entrambe le parti per $e^{at}$
• A sinistra otteniamo derivate del prodotto $e^{at}\cdot y(t)$, quindi integro entrambe le parti e divido per $e^a$:

$$\begin{array}{rl}& e^{at}y(t)=\int f(t)e^{at}dt\\ & \text{Quindi:}\\ & \\ & y(t)=\frac{\int f(t)e^{at}dt}{e^{at}}\end{array}$$

| Coefficienti Variabili non omogenee

$$y^{\prime }(t)+a(t)y(t)=f(t)$$

• Calcolo $A(t)$ ovvero la primitiva di $a(t)$
• Moltiplico entrambi i membri per $e^{A(t)}$
• A sinistra ottengo la derivate del prodotto $y(t)e^{A(t)}$, quindi integro entrambe le parti e divido per $e^{A(t)}$

$$y(t)=\frac{\int f(t)e^{A(t)}dt}{e^{A(t)}}$$

| Non Lineari di 1° Ordine

Vediamo esempio con P.b.C.

$$\{\begin{array}{l}{y}^{\prime }(t)=g(t)f(y(t))f\in C^0(S)\\ y(t_0)=y_{0}g\in C^0(I)\end{array}$$

• Controlliamo se i dati iniziali appartengono ai rispettivi domini, quindi se $y_0\in S$ e se $t_0\in I$
• Controlliamo se c’è una soluzione stazionaria, infatti se esiste un numero $y_0$ tale che $f(y_0)=0$ allora una soluzione sarà $y(t)=y_0$ ma non è detto che sia l’unica. Questo accade perché avendo 0 al secondo membro otteniamo la derivata di una costante che sarà sempre 0. (si fa alla fine)
• Studiamo il caso $f(y_0)\ne 0$, quindi studiamo la funzione finché $f(y_t)$ non si annulla.
• Dividiamo per $f(y(t))$ entrambi i membri e integriamo le due parti:

$$\int \frac{y^{\prime }(t)}{f(y(t))}dt=\int g(t)dt$$

• Sostituire dato iniziale per trovare $c$
• Calcolare il dominio per vedere dove si annulla

Esempio

Esempio

2° Ordine Omogenee

$$a{y}^{\prime \prime }(t)+b{y}^{\prime }(t)+cy(t)=0$$

• Scrivere il polinomio caratteristico $a{\lambda }^2+b\lambda +c=0$ e risolverlo
• In base alle soluzioni trovate scriviamo la soluzione generale:
  • ${\lambda }_1\ne {\lambda }_2$ → $y(t)=c_1{e}^{{\lambda }_{1}t}+c_2{e}^{{\lambda }_{2}t}$
  • ${\lambda }_1={\lambda }_2$ → $y(t)=c_1{e}^{\lambda t}+c_{2}t{e}^{\lambda t}$
  • $\lambda =\alpha \pm i\beta$ (2 zeri complessi coniugati) → $y(t)=c_1{e}^{\alpha t}\cos (\beta t)+c_2{e}^{\alpha t}\sin (\beta t)$

2° Ordine non Omogenee

Stanno scritte sopra :(