Logica degli Enunciati o Proposizioni

Per descrivere gli enunciati utilizziamo:

• Simboli Atomici
• Variabili (A, B, C)
• **Connetivi:
  • $\neg$ NOT
  • $\wedge$ AND
  • $\vee$ OR
  • $\to$ Implica
  • $\leftrightarrow$ Se e solo se

Ogni variabile è una formula, quindi se $P$ è una formula allora anche $\neg P$ lo è. Se $P$ e $Q$ sono formule allora anche $PconnettivobinarioQ$ è una formula.

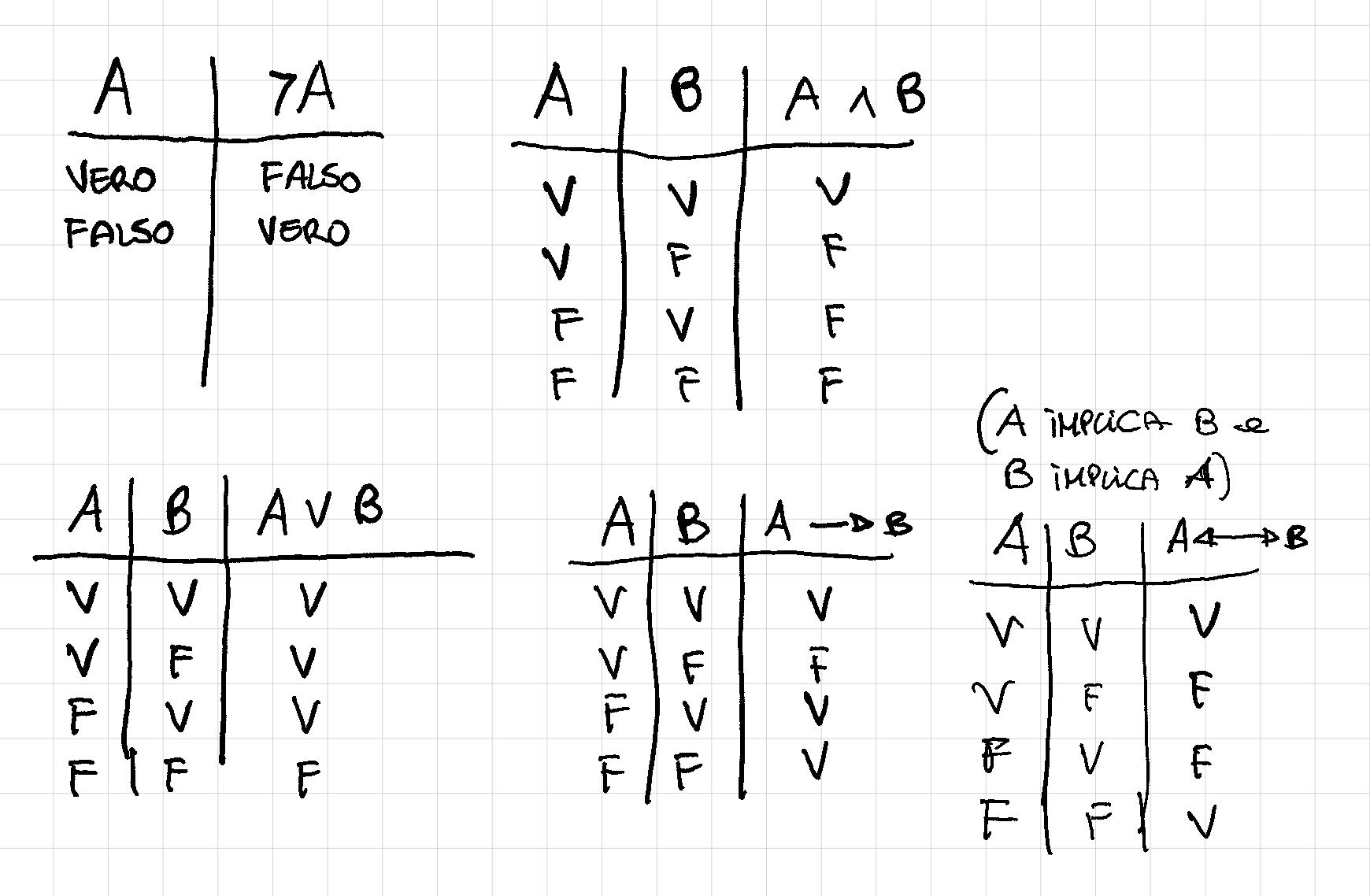
Definizioni

Una formula si dice Soddisfacibile quando è vera per qualche assegnamento

Una formula si dice Falsificabile quando è falsa per qualche assegnamento

Una formula si dice Insoddisfacibile quando è falsa per ogni assegnamento

Una formula si dice Valida quando è vera per ogni assegnamento (Tautologia) In questo caso il risultato della formula non dipende da come la interpretiamo ma è vera in generale per la sua struttura.

Esempi

$(A\to B)\wedge (A\to C)$ è Soddisfacibile (A = vero) ma anche Falsificabile (A = Vero e B = Falso)

$(A\to B)\leftrightarrow (\neg A\vee B)$ Logicamente Equivalente

Conseguenza Logica

$A_1...A_n⊢B$ | B è conseguenza logica di A

Se A è vero lo è anche B

Esercizio

Se il Milan ha vinto la partita allora il Brescia e il Piacenza retrocedono. Se almeno una tra Brescia e Piacenza retrocedono allora il Torino si salva. Quindi se il Torino non si salva allora il Milan non ha vinto la partita Costruiamo la tavola di verità:

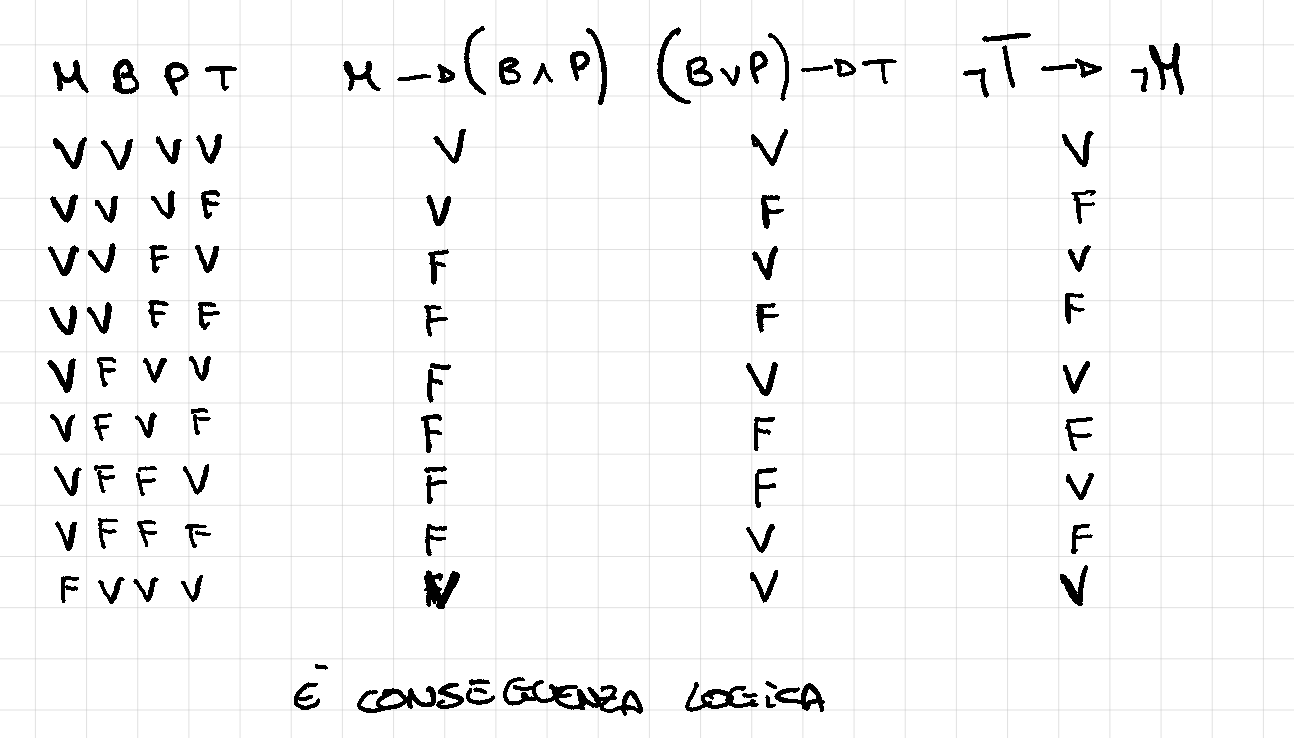
É conseguenza logica perché per provare il contrario dovremmo trovare nella tavola di verità un caso in cui le prime due condizioni sono vere e la conseguenza è falsa

Metodo dei Tableux

Sintassi Utilizzata