Cardinalità
Indica il numero di elementi che appartengono ad un insieme finito. Due insiemi che hanno lo stesso numero di elementi si dicono equipotenti ed hanno quindi una corrispondenza biunivoca tra essi
Un insieme in corrispondenza biunivoca con si dice numerabile
Vediamo qualche caso particolare
è numerabile?
Potremmo associare ad ogni coppia del prodotto cartesiano un numero naturale andando avanti sul secondo valore della coppia, quindi:
Così facendo non finiremo mai di associare numeri a coppie, dobbiamo quindi cambiare approccio.
Possiamo utilizzare la tecnica “dovetailing”, ovvero con una tabella associamo ad ogni coppia la casella dove si incontrano i suoi valori e all’interno della stessa casella scriviamo il numero naturale associato, riempiamo però la tabella in diagonale:
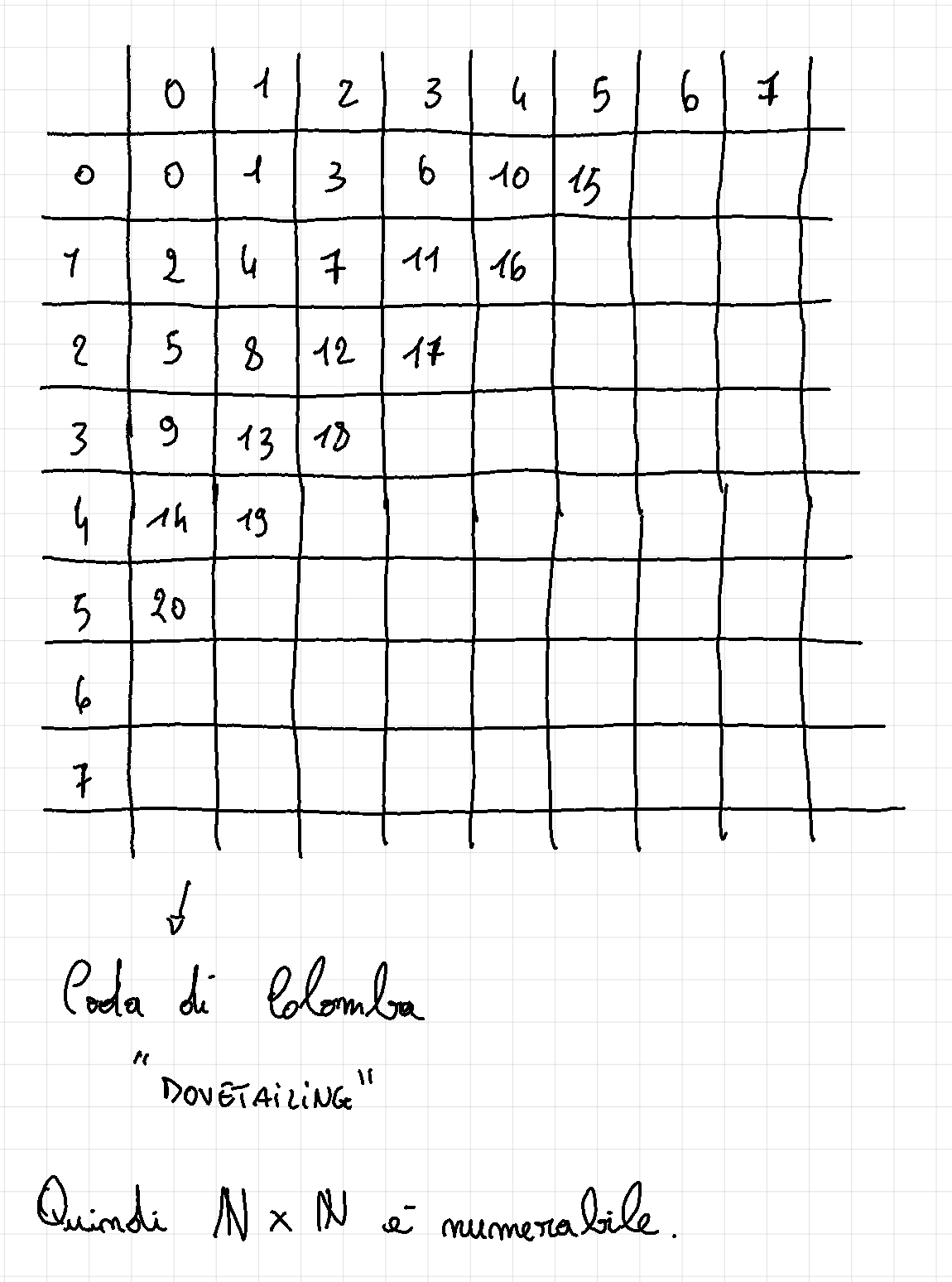
Il prodotto cartesiano è quindi numerabile
L’insieme delle parti di è numerabile?
Facciamo una dimostrazione per assurdo, partiamo quindi negando cosa vogliamo dimostrare supponendo che sia numerabile
indica la funzione caratteristica dell’insieme A, ovvero quella funzione che preso come argomento un valore, restituisce 1 se il valore appartiene all’insieme e 0 se non appartiene.
Costruendo una tabella simile alla precedente dove inseriamo nelle colonne ogni sottoinsieme possibile mentre ogni riga ci indica a quale elemento ci stiamo riferendo, l’insieme delle parti sembrerebbe numerabile
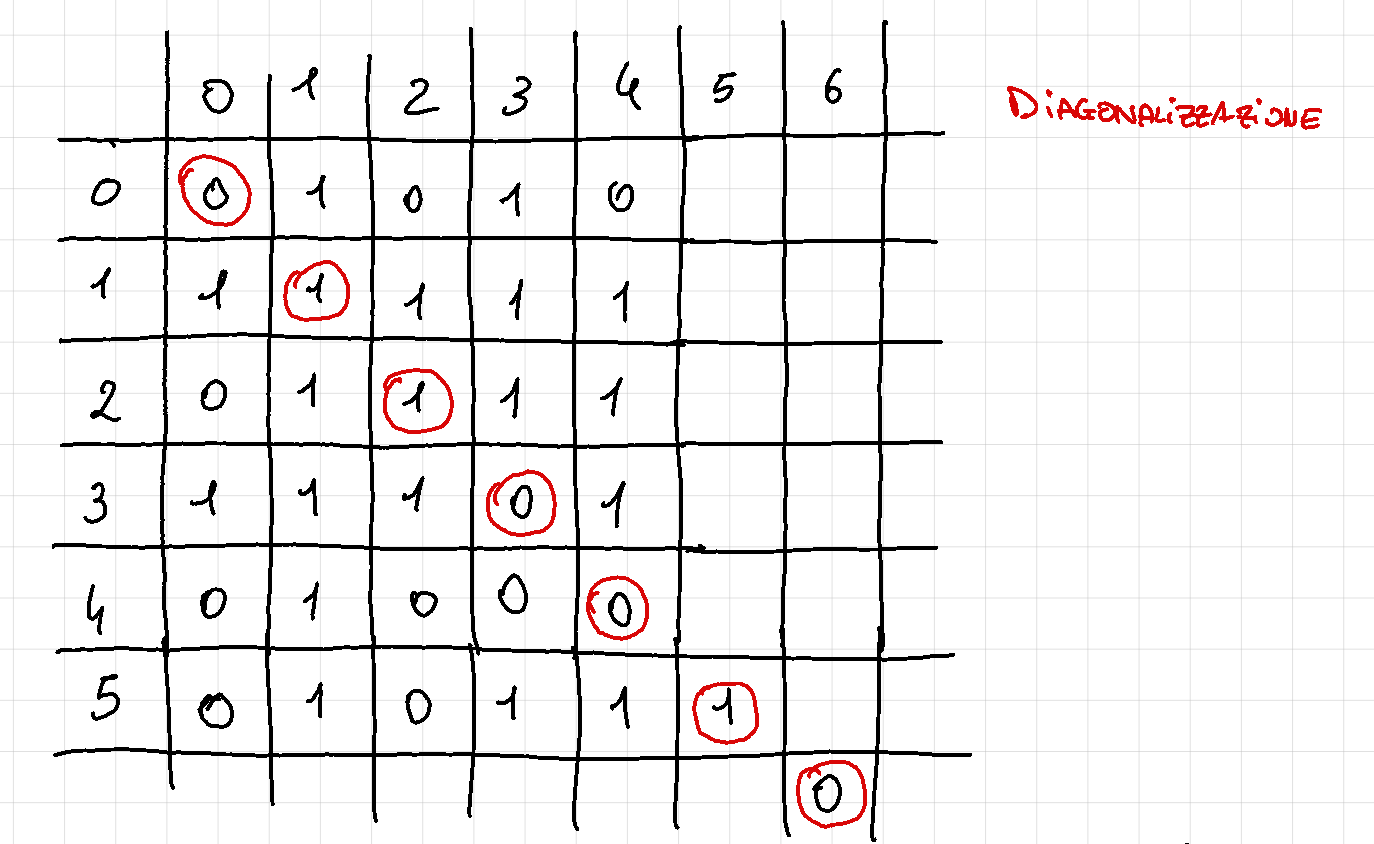
Siccome abbiamo supposto che l’insieme delle parti è numerabile significa che nella nostra tabella compaiono tutti i sottoinsiemi possibili di . Indichiamo con D l’insieme diagonale evidenziato in rosso e con il suo insieme complemento che prima o poi comparirà nella tabella. Quando i due insiemi si incontreranno non sapremo cosa inserire nel riquadro perché l’elemento corrispondente può appartenere soltanto ad uno dei due insiemi.
L’insieme delle parti di non è numerabile.